SV波垂直入射下典型框架结构对地震动影响定性研究*
2024-04-19白翔翔刘启方
白翔翔, 刘启方
(苏州科技大学江苏省结构工程重点实验室,苏州 215004)
0 引言
地震来临时,地震波经由土体传入基础,再经基础传给结构从而引起结构的振动。而结构振动又会经基础传播至土体,从而影响土体的振动,此时结构可以看作是二次振源。为了研究结构对土体振动的影响,1970年Jennings[1]在加州理工学院的密立根图书馆进行了由两个共振发生器引起的共振实验,结果在距大楼几公里的地方记录到了由大楼共振引起的地面运动。1991年Kanamori等[2]研究了哥伦比亚号、亚特兰蒂斯号和发现号航天飞机飞行路线上建筑物受冲击波的影响,并在附近观测站记录到了因高层建筑振动激发的地震响应。1993年Çelebi[3-4]研究了美国Whittier-Narrows地震中的两相邻7层排架及周边地表强震观测数据,结果表明结构对周边土体振动产生了影响。2002年CHVEZ-GARCA F J等[5]分析了环境噪声和土-结构相互作用下自由场的地震动,结果表明在这两种相互作用下,所产生的波场可能会影响自由场的震动。2003年张菁莉等[6]采用二维整体有限元法研究了两相邻25层高层建筑,分析了场地条件对单一结构和相邻结构之间地震动的差异,结果显示土体越软结构间距对地震反应的影响越明显。2005年GUÉGUEN P等[7]在欧洲Volvi试验场研究了建筑物振动对地表运动的影响,结果表明结构振动对地震动的影响不可忽视,可能会干扰周围的地面运动。
为分析单体框架结构存在对土体地震动的影响,依据《建筑抗震设计规范》(GB 50011—2010)[8]建立了满足国内标准的四类场地土体模型和三种不同大小框架结构模型。利用三维显-隐式分区算法采用传递函数,分析了在SV波垂直入射下框架结构对周围地震动的影响与场地类别、框架结构大小和土体距结构距离的关系。
1 研究方法
目前土-结构相互作用常用的研究方法有集中参数法[9]、子结构法[10]、直接法[11]。集中参数法和子结构法通常只适用于线性系统,而直接法体系的计算量大,计算效率较为低下。由于本文采用三维土体和结构模型,计算量甚大,故采用陈少林[12-14]等提出的一种高效三维显-隐式分区算法模拟结构和土体的地震反应。
1.1 上部结构的运动
上部结构运动方程见式(1)。
Mu″+Cu′+Ku=F
(1)
式中:M为集中于节点的质量矩阵;C和K分别为节点和相邻节点之间的阻尼矩阵和刚度矩阵;u″、u′、u分别为节点的加速度向量、速度向量和位移向量;F为合力。
采用Newmark隐式积分算法结合式(2)得到p+1时刻的位移:
(2)
式中:β和γ为按积分精度和稳定性要求进行调整的参数;Fp+1为t=(p+1)Δt时刻节点a的合力,Δt为时间步距;up+1为节点在t=(p+1)Δt时刻的位移向量;up、up′、up″分别为节点在t=pΔt时刻的位移、速度和加速度向量。
1.2 土体的运动
土体节点可分为土体内部节点、人工边界点和土体与基础相连的节点。与基础相连节点的运动由基础运动决定。
1.2.1 内部节点运动
土体内部节点运动方程见式(3)。
(3)
式中:ma为集中于土体内节点a的质量;Cab为节点a与相邻节点b之间的阻尼矩阵;Kab为节点a与相邻节点b之间的刚度矩阵;n为与节点a相邻的节点总数;uap、uap+1和uap-1分别为节点a在t=pΔt、t=(p+1)Δt和t=(p-1)Δt时刻的位移;ubp和ubp-1分别为节点b在t=pΔt和t=(p-1)Δt时的位移;Fap为t=pΔt时刻节点a的合力。
1.2.2 土体边界点的运动
采用刘晶波等[15-16]提出的黏弹性动力人工边界。将人工边界等效为弹簧阻尼系统,见图1,其中k和c分别为粘弹性边界弹簧和阻尼系数。
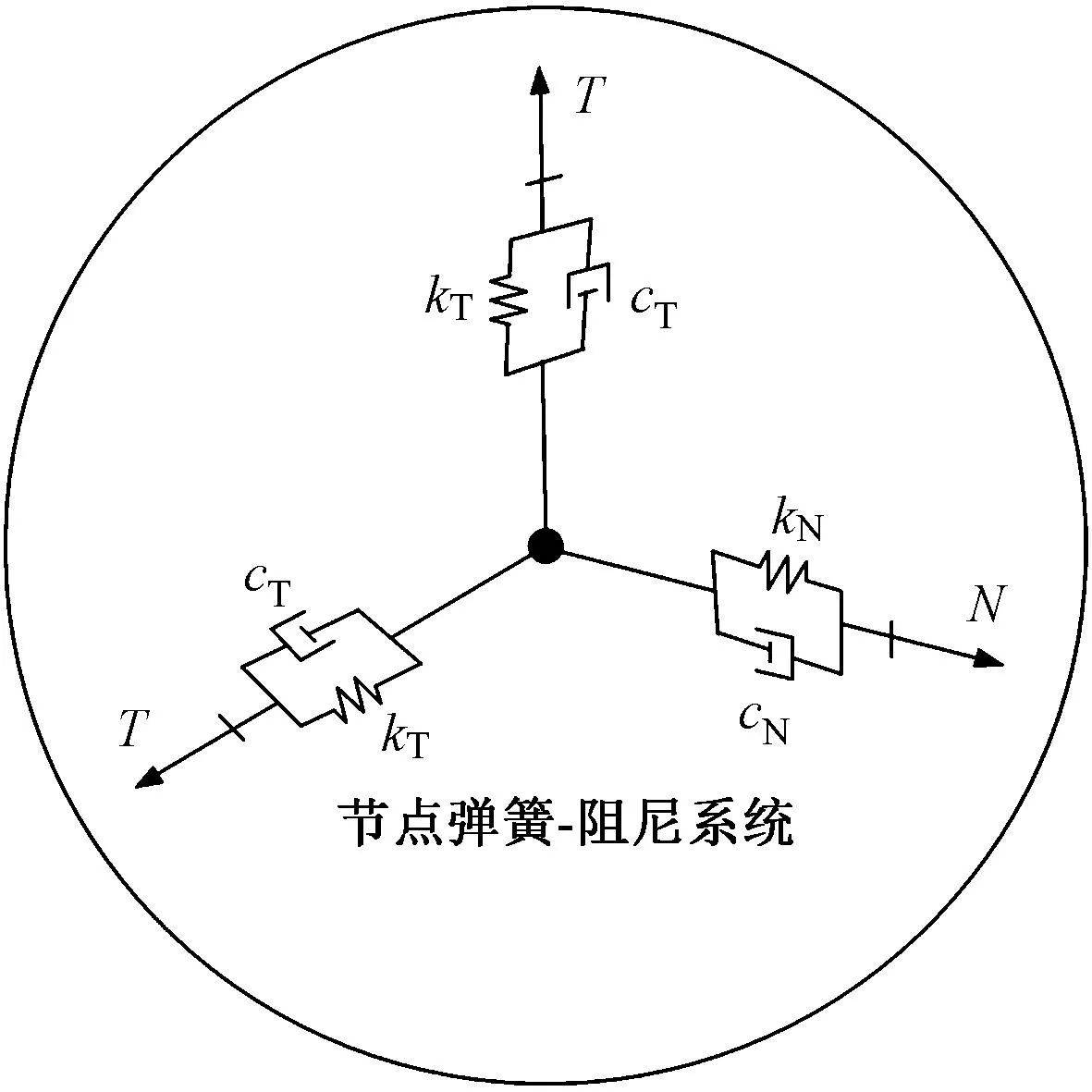
图1 人工边界等效示意图
(4)
式中:kN、kT分别为弹簧法向和切向刚度;cN和cT分别为阻尼器法向和切向阻尼系数;R为波源到人工边界点的距离;cS为S波波速;cp为P波波速;G为介质的剪切模量;ρ为介质密度;αN和αT分别为黏弹性人工边界的法向和切向修正系数,取αN=1.33,αT=0.67[16]。
通过转化为法向和切向等效节点力的方式实现地震波的输入:
(5)
边界点上施加的等效力FB为:
(6)
式中S为边界点所代表的面积。
1.3 基础的运动
将基础假定为刚性基础,其运动方程见式(7)。
MFUF″=Fs+Fb
(7)
式中:MF为基础的质量矩阵;UF″为基础的加速度;Fs为土体对基础的合力;Fb为上部结构对基础的合力。
由中心差分格式得:
UFP+1=2UFP-UFP-1+UFP″Δt2
(8)
式中:UFP+1、UFP、UFP-1分别为p+1、p、p-1时刻的位移;UFP″为p时刻加速度;Δt为时间步距。
显-隐式时域土-结构相互作用的并行计算通过MPI(message passing interface)通讯协议实现。
2 模型参数
2.1 场地模型
建立土体模型如图2所示,尺寸为600m(X向)×240m(Y向)×100m(Z向),并离散为2m×2m×2m的六面体八节点实体单元,单元数为180万。将土体沿X向划分为5个子区域。四类场地土体参数如表1所示。
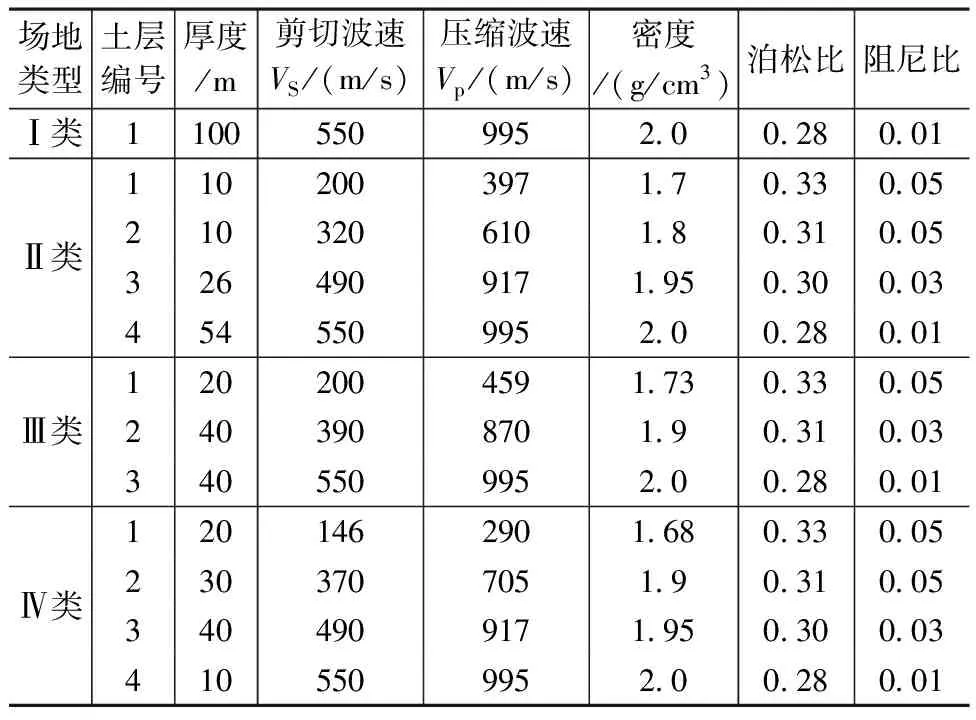
表1 四类场地土体参数
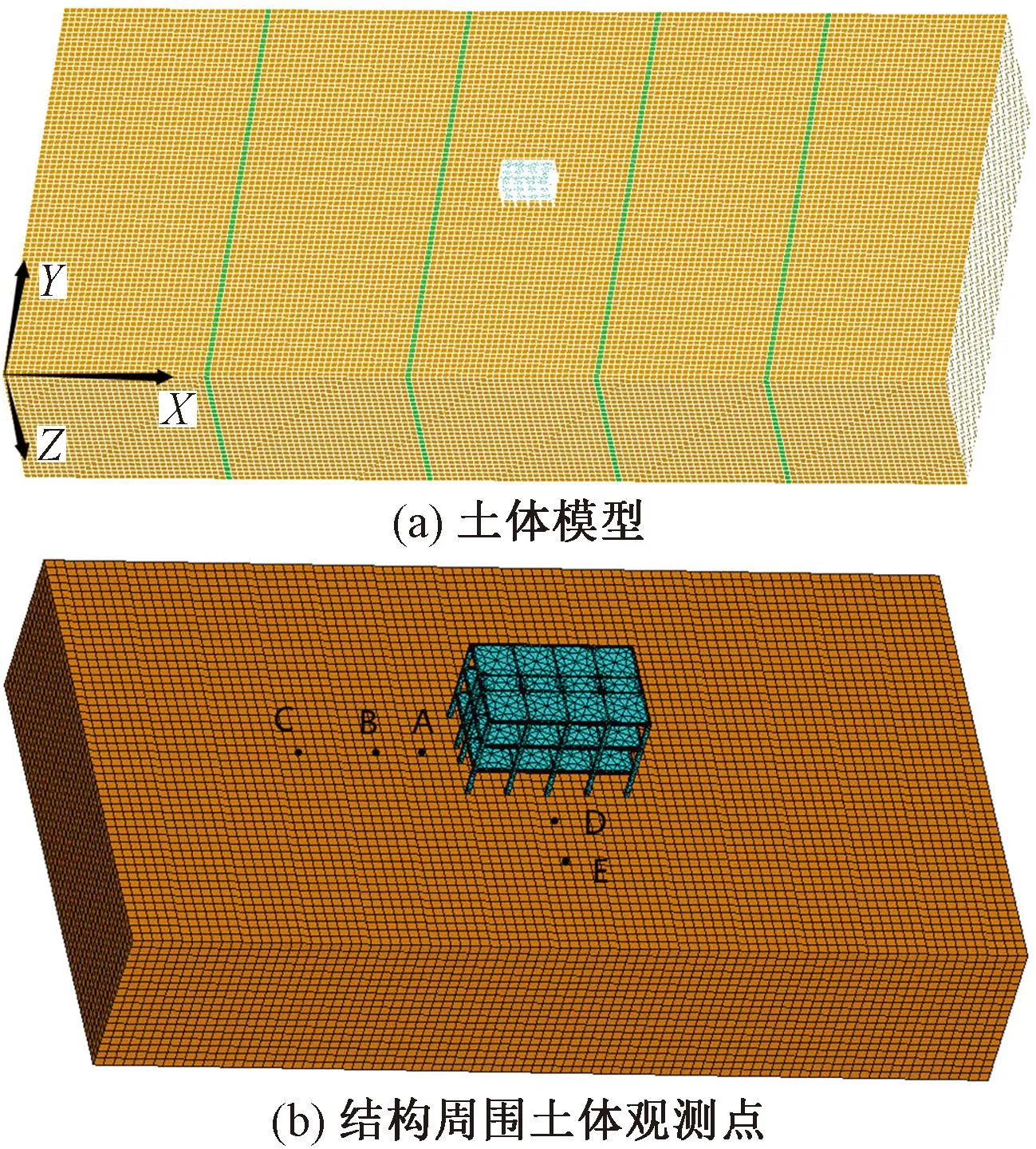
图2 土体模型示意图
2.2 结构模型
框架结构基本参数如表2所示。混凝土的弹性模量为30GPa,密度为2 500kg/m3,泊松比为0.2。使用ANSYS单独对框架结构进行模态分析,其中3层结构一阶频率为4.423Hz,二阶频率为5.268Hz;7层结构一阶频率为2.324Hz,二阶频率为3.582Hz;11层结构一阶频率为1.445Hz,二阶频率为2.723Hz。框架结构有限元模型见图3。
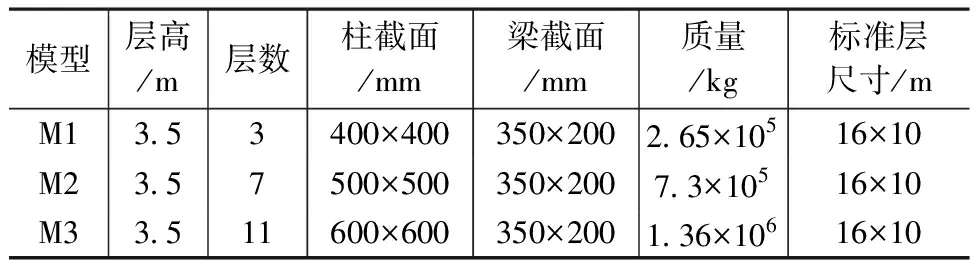
表2 框架结构基本参数
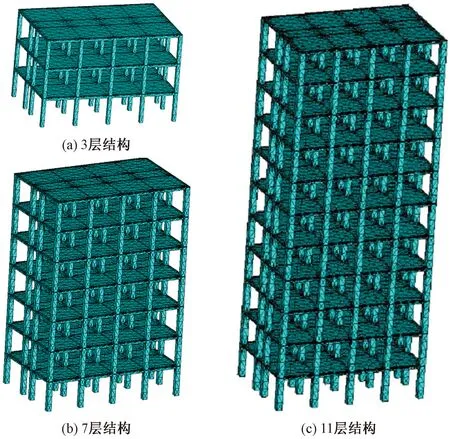
图3 结构模型示意图
选取脉冲宽度0.1s的单位脉冲波作为SV波垂直入射,时间步距5×10-5s,计算步数为50 000步,输入脉冲波的位移时程和位移频率谱如图4所示。
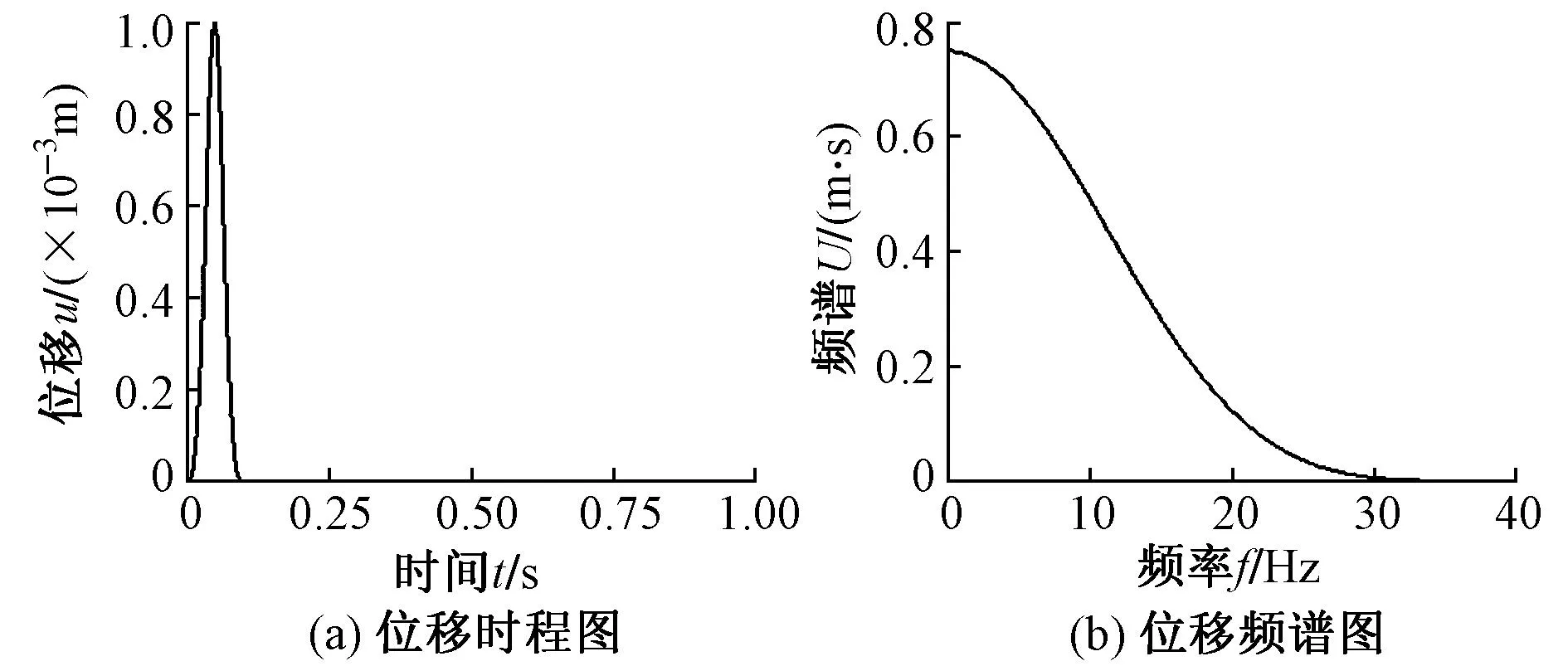
图4 输入单位脉冲
3 结果分析
由于三维土-结构相互作用计算量很大,结论的具体量化需大量模型计算及系统分析。本文通过三种常见典型框架结构和四类场地模型,针对框架结构对地震动的影响开展初步的定性研究。
采用传递函数来分析结构存在对地震动的影响,传递函数定义为各点的傅里叶位移振幅谱与输入脉冲谱的比值。由于SV波垂直入射主要产生X向的响应,这里只给出X向结果。为研究结构存在对地震动的影响与土体距结构距离的关系,分别给出结构左侧距基础10、30、70m的A、B、C三点和基础前方距基础20、50m的D、E两点(图2(b)),共5点自由场(无结构)和存在三种结构时的结果。
图5给出了四类场地下模型A点的传递函数。Ⅰ类场地条件下(图5(a)),7Hz以下三种结构对地震动均未产生明显影响,7~19Hz则出现压制现象,19Hz几乎无影响,19~25Hz产生放大作用。Ⅱ类场地条件下(图5(b)),4Hz以下三种结构对地震动影响较小,4~8Hz(包括8Hz)产生压制现象,8~14Hz地震动出现明显放大现象。Ⅲ类场地条件下(图5(c)),3.5~7Hz频段内地震动因结构存在出现压制现象,11~14Hz有放大现象。Ⅳ类场地条件下(图5(d)),仅在2.5~4.5Hz处结构存在对地震动产生压制现象。
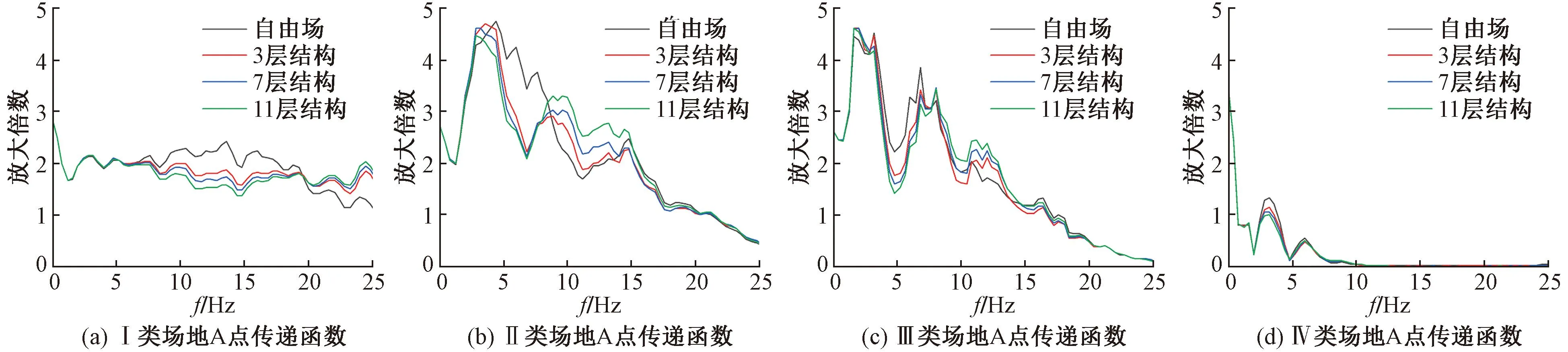
图5 四类场地模型A点传递函数
对比四类场地结果可见,结构存在下Ⅰ、Ⅱ类场地地震动出现了明显的先压制后放大,其中Ⅰ类场地受压制的频段最宽频率较高,随着土体变软,由于土的滤波作用,结构存在对地震动的压制频段逐渐变窄且频率随之降低。
进一步分析三种不同结构对地震动的影响,Ⅰ类场地条件下(图5(a)),三种结构对地震动影响差异明显,3层结构(红色曲线)与自由场(黑色曲线)差异最小,11层结构(绿色曲线)与自由场差异最大。这表明在Ⅰ类场地条件下结构对地震动的影响可能与框架结构大小成正相关。Ⅱ类场地条件下(图5(b)),4~8Hz(包括8Hz)三种结构对地震动影响较为接近,未因结构大小变化出现明显差异,8~14Hz三种结构对地震动影响出现较大差异,地震动受结构大小变化影响明显。Ⅲ类场地下(图5(c)),7~11Hz频段内7层结构(蓝色曲线)对地震动基本未产生影响,而3层结构对地震动产生压制,11层结构则对地震动有放大。这表明Ⅲ类场地下结构大小对地震动的影响并不是简单的正相关。Ⅳ类场地条件下,三种结构对地震动的影响均较小。
为进一步分析土体与结构距离对地震动的影响,图6给出了距A点仅20m处B点(距基础30m)四类场地传递函数。图中可见随距离增大地震动受结构影响显著减弱。特别是在Ⅳ类场地条件下(图6(d)),B点处可基本忽略结构对地震动的影响。
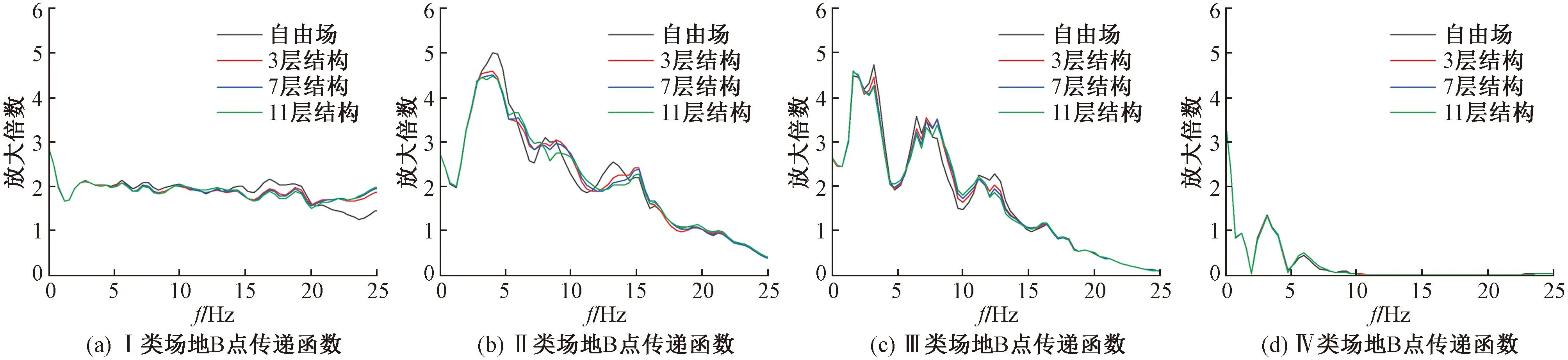
图6 四类场地模型B点传递函数
Ⅰ类场地条件下B点处(图6(a)),14Hz以下三种结构均未对地震动产生明显影响,而A点在7~19Hz地震动因结构存在出现压制。Ⅱ类场地条件下(图6(b)),11~14Hz结构对地震动产生压制效果,A点则因结构地震动出现放大。Ⅲ类场地条件下(图6(c)),11~13Hz结构对地震动产生压制效果,而A点处11~13Hz频段内,结构存在对地震动产生放大。Ⅰ、Ⅱ、Ⅲ类场地A、B两点在部分相同频段下地震动影响不同,表明结构存在时因土体与结构距离不同在相同频段地震动可能产生不同影响。
随着土体与结构距离继续增大,C点(距基础70m)处地震动受结构的影响进一步减小。与Ⅳ类场地类似(图7(d)),Ⅲ类场地条件下(图7(c)),C点处结构对地震动影响也可基本忽略。

图7 四类场地模型C点传递函数
通过比较自由场及三种不同结构存在下,四类场地距基础由近到远的A、B、C三点地震动反应可见,在距基础仅10m的A点处Ⅰ、Ⅱ、Ⅲ类场地条件下三类结构对地震动的影响出现明显差异,而在Ⅳ类场地条件下结构对地震动的影响最小且因结构大小不同引起的地震动差异最小。土体与结构距离增大,结构对地震动的影响迅速衰减,在距A点仅20m的B点,Ⅳ类场地条件下已看不出结构对地震动的影响,且此时其他三类场地不同大小结构对地震动的影响也较为相似。随着距离进一步变大,在距基础70m的C点Ⅲ、Ⅳ类场地条件下结构对地震动影响基本可以忽略,Ⅱ类场地条件下7~10Hz频段内结构存在虽对地震动有影响,但此时三种结构对地震动的影响基本相同。Ⅰ类场地条件下C点处结构对地震动仍有明显影响,且此时仍能看出三种结构对地震动的影响差异。
图8、9给出了结构前方与基础距离不同的D、E两点传递函数,由图中可见,不同于结构左侧,在SV波垂直入射下三种结构对基础前方地震动产生影响相似,结构大小的变化并未对地震动产生明显不同的影响。

图8 四类场地模型D点传递函数
在Ⅱ类场地条件下(图8(b)),D点8~14Hz频段内,结构越大对地震动的影响越小,同一场地条件下(图9(b),E点5~9Hz同样是结构越大对地震动的影响越小。这表明在Ⅱ类场地条件下结构对地震动的影响还与相对基础的位置、距离有关。
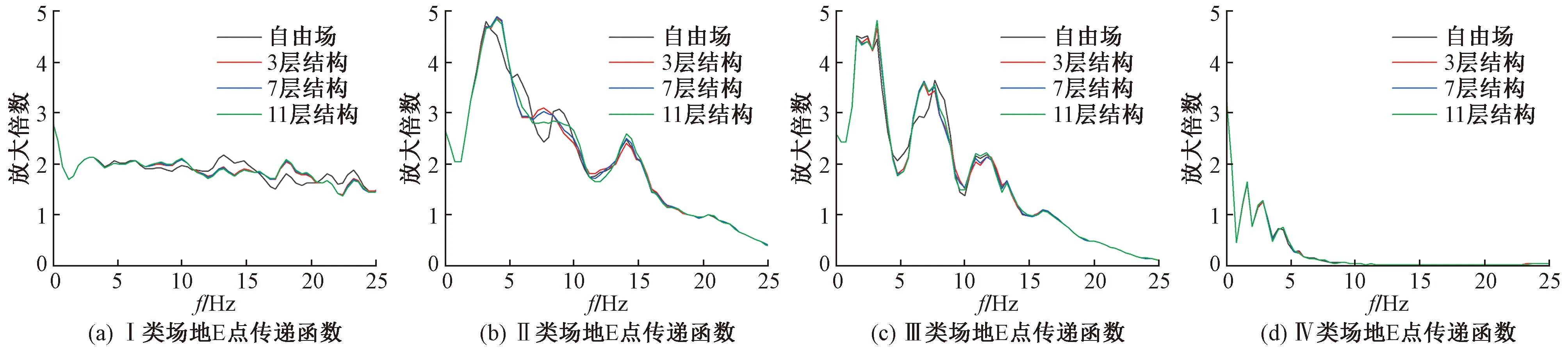
图9 四类场地模型E点传递函数
4 结论
本文建立了四类场地土体模型和三种典型框架结构模型,采用三维显-隐式分区算法模拟了SV波垂直入射下框架结构对周围土体震动的影响,并利用传递函数分析了框架结构对地震动的影响与场地类别、结构大小和土体与结构距离的关系。结果表明:
(1)单体框架结构对地震动的影响局限在结构附近很窄的范围内,随土体与基础的距离的增大,迅速衰减。不同场地条件下,框架结构对地震动的影响有显著差异,Ⅰ类场地影响范围最大,结构对地震动的影响衰减最慢,随土体变软,由于土的滤波作用增大,结构对地震动的影响范围逐渐变小,影响频段也逐渐变窄且向低频移动。
(2)不同大小框架结构对地震动的影响和场地有关,Ⅰ类场地条件下结构对地震动的影响与结构大小可能成正相关。而Ⅱ、Ⅲ类场地条件下结构对地震动的影响较为复杂,与地震动的频带和土体与基础距离有关,同一频带下,距离不同可能正相关亦可能负相关。Ⅳ类场地条件下框架结构大小的改变对地震动没有显著影响。
本文通过对场地类别、结构大小和土体与结构距离的分析,初步探讨了典型框架结构对地震动影响的定性关系。而结构质量、自振频率及体系阻尼比等特性可能对不同频段下的地震动有重要影响,具体的量化影响效果将在后续工作中进一步研究。
