基于同伦延拓的冗余机械臂逆运动学优化算法研究
2024-04-19张国庆李宗道吴剑雄顾浩宇李清都
张国庆,李宗道,吴剑雄,顾浩宇,李清都
基于同伦延拓的冗余机械臂逆运动学优化算法研究
张国庆,李宗道,吴剑雄,顾浩宇,李清都*
(上海理工大学,上海 200093)
针对偏置冗余机械臂的逆运动学,采用传统数值法存在依赖初始值、奇异位姿收敛性差等问题,提出一种改进数值法。首先将非线性方程组转化为同伦方程组,引入同伦延拓算法能够有效避免依赖初始值的问题,同时能够获取逆运动学解空间。然后考虑奇异位姿,将同伦方程组转化为最小二乘问题,采用Levenberg Marquardt算法对同伦方程组进行路径追踪,以获取逆运动学解空间。最后将关节极限避免问题映射为解空间优化问题,引入二进制改进粒子群优化算法,获得最优逆运动学解。实验结果表明,相较于传统数值法,文中所提数值法针对逆运动学求解具有更高的收敛率、更快的收敛速度,同时二进制改进粒子群算法能够有效避免关节极限问题。采用文中所提数值法求解逆运动学的精度较高,能够满足实时性要求,对于机械臂用于包装作业具有一定的理论意义和工程应用价值。
冗余机械臂;逆运动学;Levenberg Marquardt;同伦延拓;二进制改进粒子群算法
机器人技术广泛应用于包装行业,针对包装的不同类型(如产品装箱、分拣等),需要机械臂高速、高精度地操作,以提高其生产效率。冗余机械臂关节空间的维数大于任务空间的维数,导致七自由度机械臂逆运动学欠约束[1],增大了逆运动的复杂性。
许多学者已经提出了多种方法来解决冗余自由度机械臂的逆运动学问题,其中包括基于位置的解析法[2]、基于智能优化算法求解和基于雅可比的数值解。在2007年,Shimizu等[3]引入“臂角”的概念,并作为参考平面来描述肘部的自运动特性,进而推导出期望肘部位置时所有关节的表达式。基于位置的解析方法对机械臂的几何构型提出了较高的要求,因此不适用于带偏置结构的机械臂。
近年来,智能算法通过将机器人运动学方程转化为最优控制问题进行求解。这类算法主要包含粒子群优化算法(Partical Swarm Optimization, PSO)[4]、遗传算法(Genetic Algorithm, GA)[5]、神经网络算法(Neural Network Algorithm, NNA)[6]和模拟退火算法(Simulated Annealing Algorithm, SAA)[7]。虽然优化算法能够有效解决奇异位姿逆运动学问题,但复杂的计算需要昂贵的时间成本,这不利于实时控制。
目前,牛顿拉夫森法(Newton Raphon, NR)[8]是最常见的数值求解方法,但是NR在以下2种情况下会收敛失败:奇异位姿、初始点距离目标点过远。房立金等[9]采用线性插值方法,在每个插值点进行逆运动学求解,逐步逼近目标点,但是未从根本上解决问题。高斯牛顿法(Gauss Newton Raphon, GNR)[10]通过最小二乘问题最小化,获取了误差最小的逆运动学解。阻尼牛顿法(Damping Newton Raphon, DNR)[11]通过在每次迭代过程中引入一个阻尼因子,能够改善DNR中存在的发散和局部最小值问题,但却降低了收敛速度。Levenberg Marquardt算法[12]结合了高斯牛顿法和阻尼牛顿法的思想,提高了算法的稳定性。Ananthanarayanan等[13]应用Levenberg Marquardt算法找到逆运动学方程组的根,具有较好的稳定性。上述数值法都不能有效避免对初始值的过度依赖性,其收敛速度较慢,易出现不收敛问题,从而影响算法的鲁棒性。
文中针对传统数值法对初始值敏感及冗余机械臂逆运动学解空间等问题,将奇异性考虑在内,提出一种改进的数值法,将Levenberg Marquardt算法与同伦延拓算法融合,以获得逆运动学解空间,并且针对关节极限规避问题进行优化处理。最后,对文中所提逆运动学算法进行仿真验证,进一步探究机械臂在包装自动化中的应用。
1 冗余机械臂运动链分析
采用带偏置七自由度机械臂,相应的MDH结构和MDH参数如图1、表1所示。
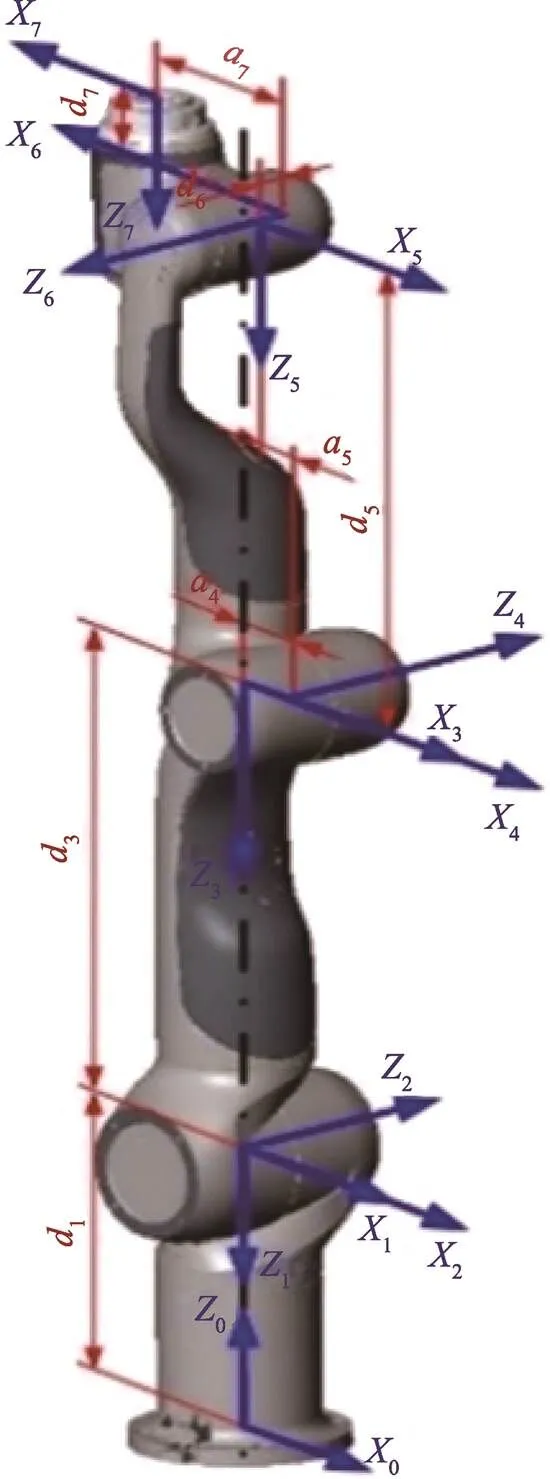
图1 七自由度机械臂MDH结构
表1 七自由度机械臂MDH参数
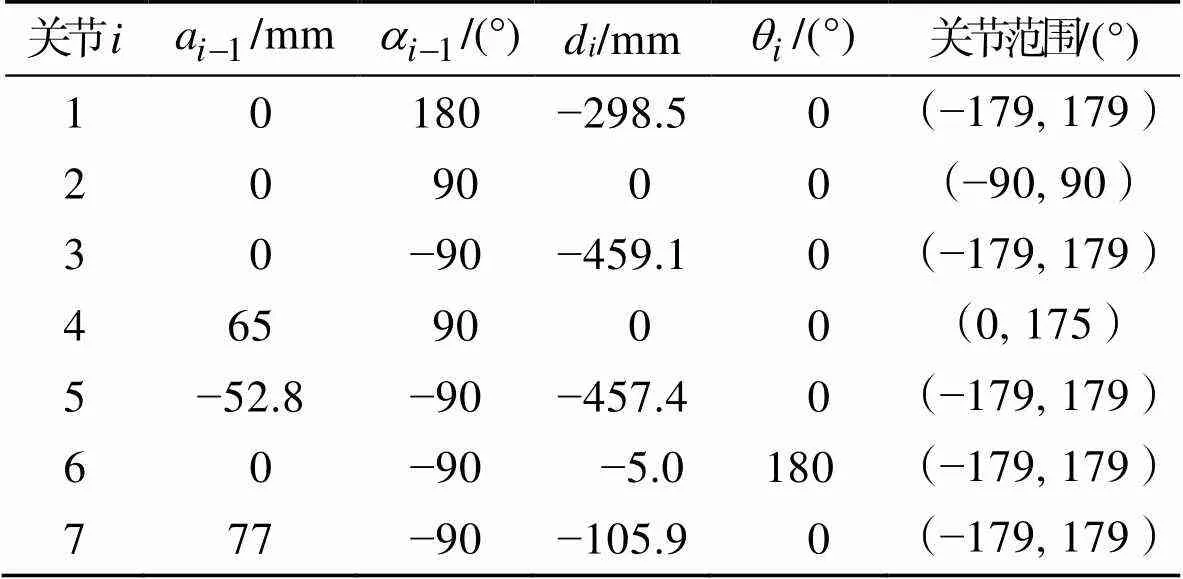
Tab.1 MDH parameters of the 7-DOF manipulator
根据MDH参数表,计算得到机械臂相邻关节之间的齐次变换矩阵,见式(1)。

当各个关节角度已知时,得出各相邻关节之间的齐次变换矩阵,将7个齐次变换矩阵相乘,得到机械臂末端位姿相对于基座的齐次变换矩阵,见式(2)。
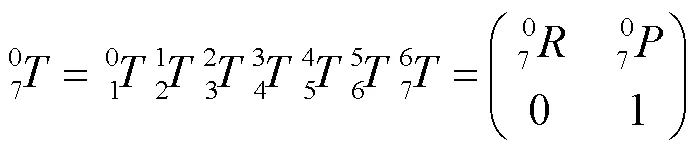
2 冗余机械臂逆运动学求解
同伦延拓算法(Homotopy Continuation Method,HCM)与传统的数值迭代法相比,具有不依赖初始值、求解效率高、只需改变辅助同伦函数就能无发散地求出方程所有解等优点[14],因此将Levenberg Marquardt(LM)算法与HCM相结合,以提高逆运动学数值法的稳定性和收敛速度。
2.1 牛顿同伦延拓算法
七自由度机械臂的逆运动学数学模型是一个混合三角函数多项式系统的高度非线性方程组,在满足末端执行器位姿的情况下,为机械臂找到一组可行的关节角度,具体方程组见式(3)。
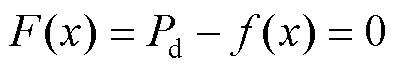
常用的牛顿法求解该方程组的迭代见式(4)。
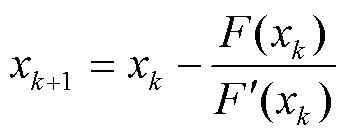
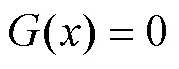
Wu[17]详细介绍了辅助同伦函数的选择依据,将同伦方程定义为式(6)。
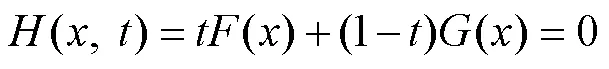
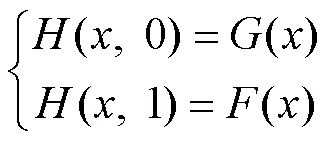

2.2 Levenberg-Marquardt同伦延拓算法
Shafiee-Ashtiani使用四阶同伦延拓算法,通过改变辅助同伦函数解决并联机械臂正运动学多解问题,并成功获取了全部16组正向运动学解。将奇异位姿考虑在内,文中采用LM算法对同伦方程进行校正,目的是避免传统数值法对初始值依赖的问题,且能够获取逆运动学解空间。
当机械臂处于奇异位姿时,LM算法通过添加阻尼项,能够有效计算出逆运动学解,并且具有更快的收敛性和鲁棒性。将式(3)表示为最小二乘最小化问题,残差的计算见式(9)。
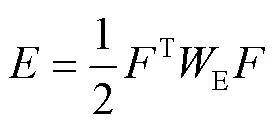
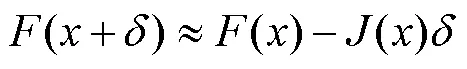
将式(10)带入式(9),并添加阻尼项,可得式(11)。
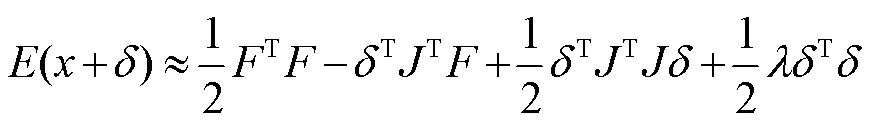
(T+λI)δ=T(12)
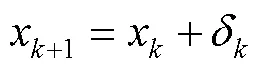

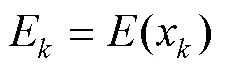
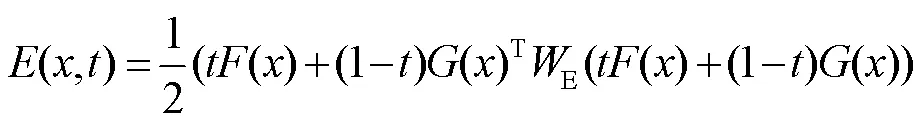

3 关节极限规避
LMHCM获取的逆运动学解空间为七维离散空间,为了在解空间中找到一组满足极限要求的最优解,将关节极限避免问题转化为最优问题。二进制粒子群优化算法(Binary Particle Swarm Optimization, BPSO)是求解二进制(离散)优化问题常用的群体智能算法之一,具有参数少、结构简单、执行速度快等特点[19]。Liegeois[20]利用机械臂的关节范围中心来优化关节运动,则任意关节的势函数见式(17)。
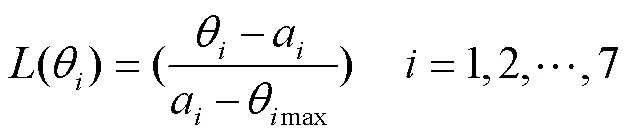
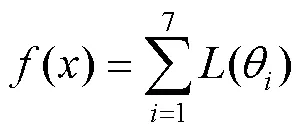
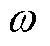
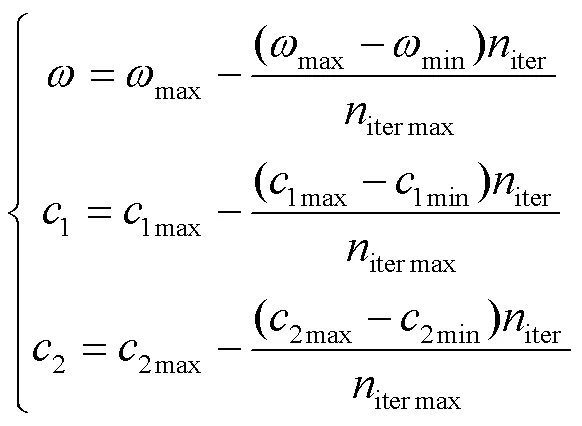

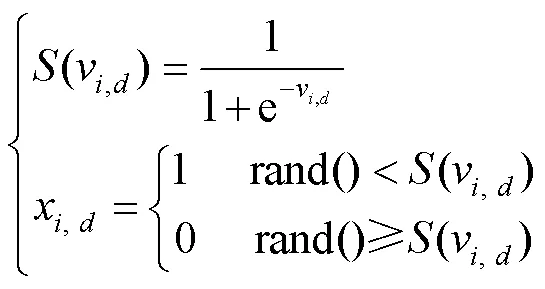
4 实验仿真验证
为了验证文中所提逆运动学算法的有效性,以冗余机械臂(图1)为例进行仿真验证,其连杆参数和关节运动范围如表1所示。实验基于AMD R7-5800H 3.2 GHz CPU的Windows系统下的Matlab 2021a进行。
4.1 逆运动学求解验证

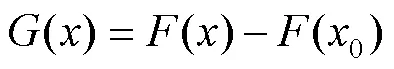
采用Matlab软件中的机器人工具箱(Robotic System Toolbox)进行仿真验证,机械臂目标位姿如图2所示。
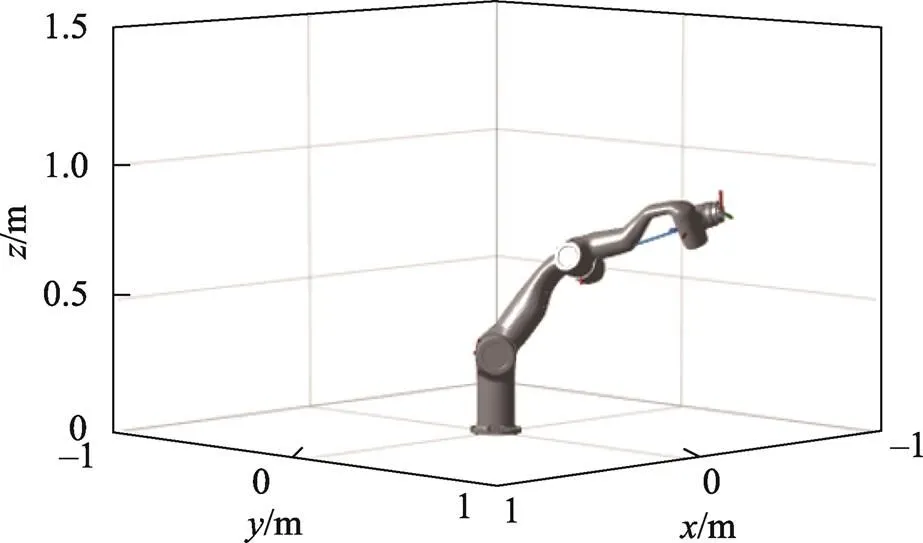
图2 机械臂目标位姿
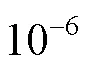
4.2 关节极限避免验证
为了验证所提关节极限避免算法的有效性,进行如下仿真。在仿真开始前,设置粒子群的数量为7,最大学习因子均为1.5,最小学习因子均为0.5,最大惯性权重为0.9,最小惯性权重为0.4,粒子的最大速度为5,最小速度为−5,且将迭代步骤的数量设置为50。研究的机械臂末端位姿见式(22),初始姿态为机械臂起始关节角度。首先,通过逆运动学求得该目标位姿对应的100组关节角度,然后根据机械臂的关节极限(表1)及式(18)建立目标函数。通过式(20)~(21)不断更新粒子的搜索方向及位置。
图4反映了SABPSO算法在搜索过程中目标函数的变化情况。当函数取值最小时,即为远离关节极限的最优关节角度。由图4可知,将文中所提的逆运动学求解方法LMHCM与SABPSO算法相结合,可以实现关节极限规避。
4.3 实验对比验证
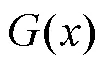
从表3可以看出,传统NR、LM算法求解逆运动学的收敛能力分别仅有37%、56%,平均运行时间需要0.126 6、0.139 5 s。虽然NRHCM算法具有较高的收敛率,但仍无法处理奇异位姿下的逆运动学,且收敛速度相较于NR、LM算法更慢,不适于实时控制。文中提出的算法LMHCM的收敛能力达到了97%,运行时间仅需0.04 s左右。可以得出结论,文中所提算法LMHCM相较于传统的数值法具有更高的收敛率和收敛速度。
表2 逆运动学解
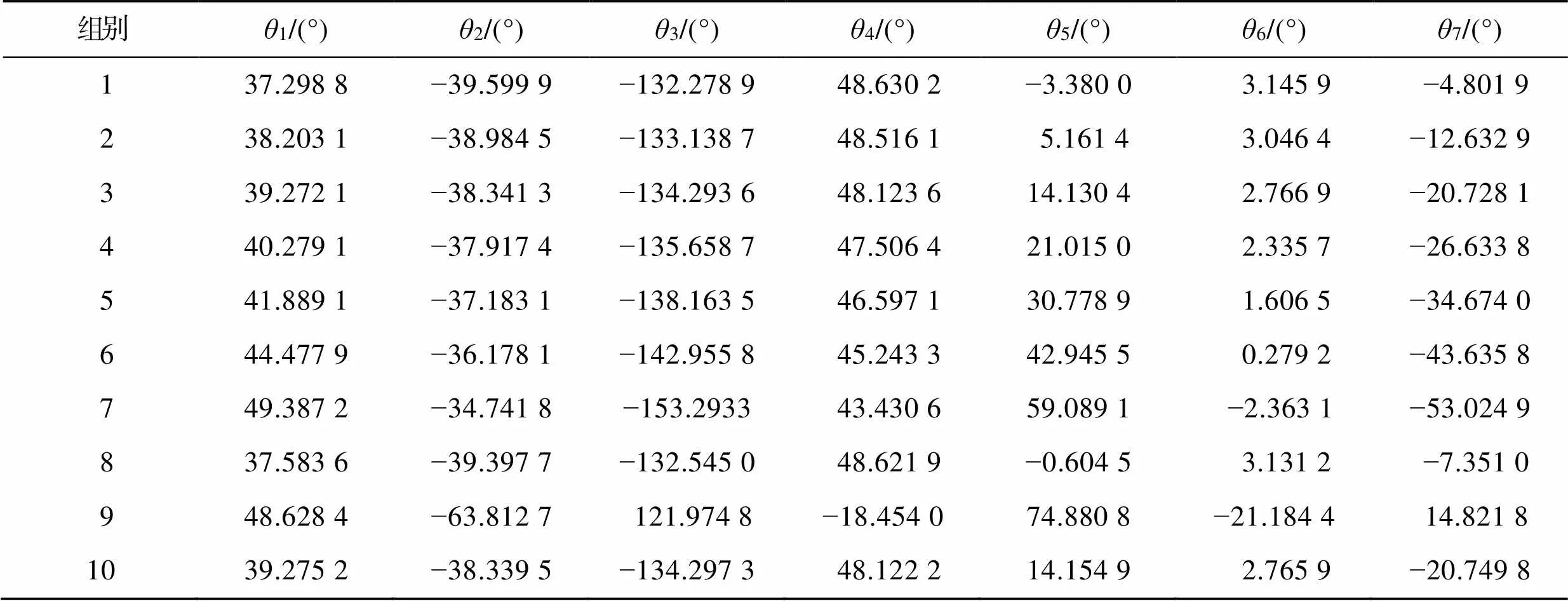
Tab.2 Inverse kinematics solution
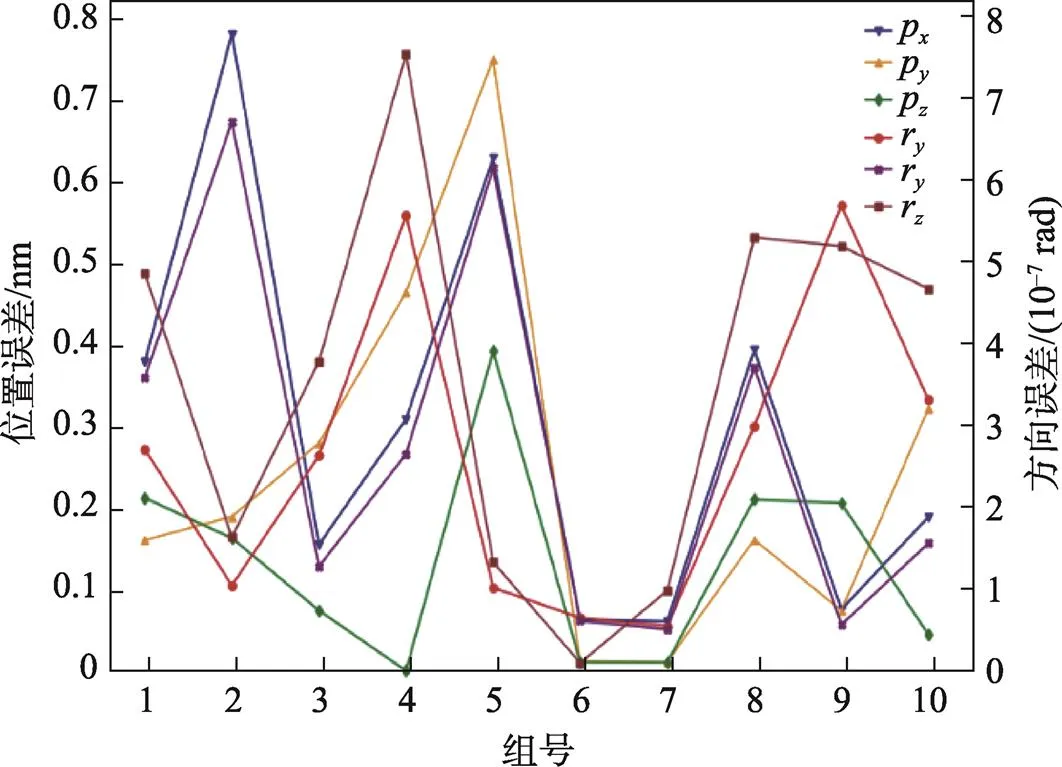
图3 位姿误差曲线
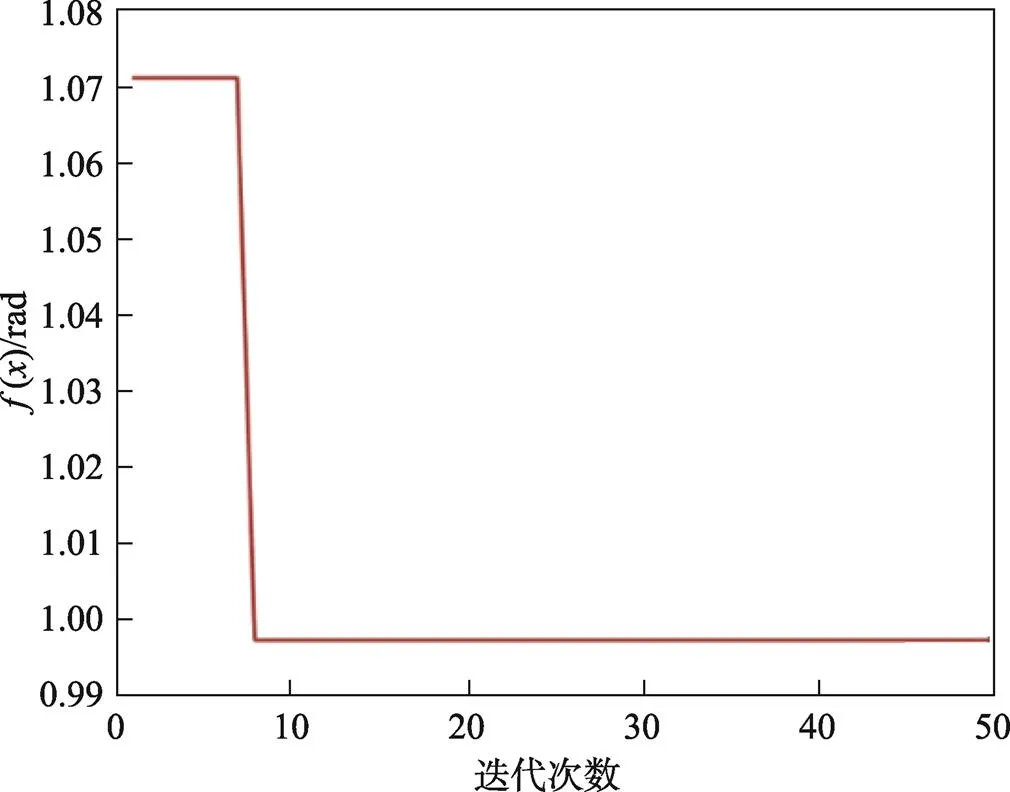
图4 适应度函数变化曲线
表3 4种数值法实验效果对比
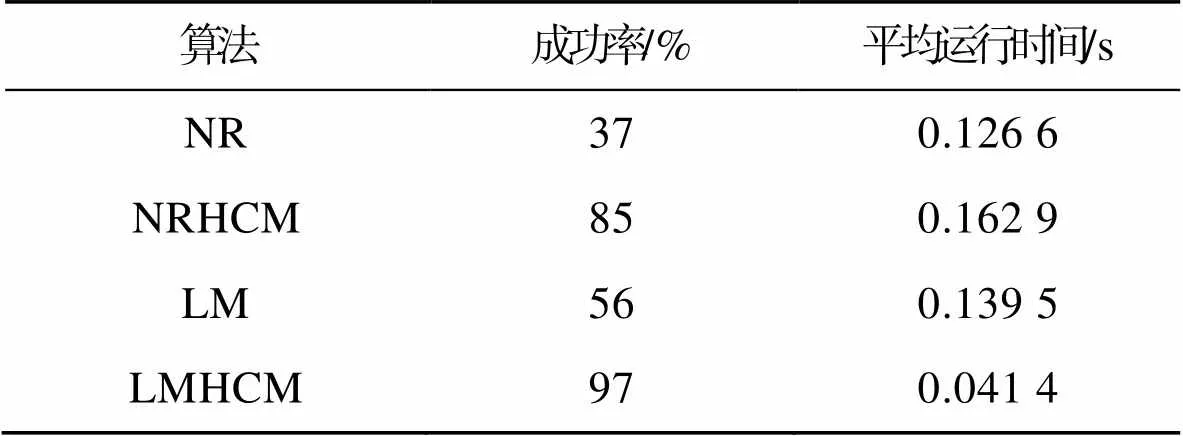
Tab.3 Comparison of experimental results of four numerical methods

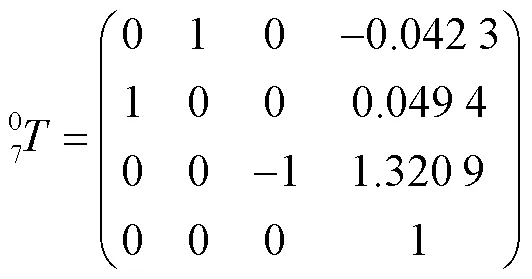
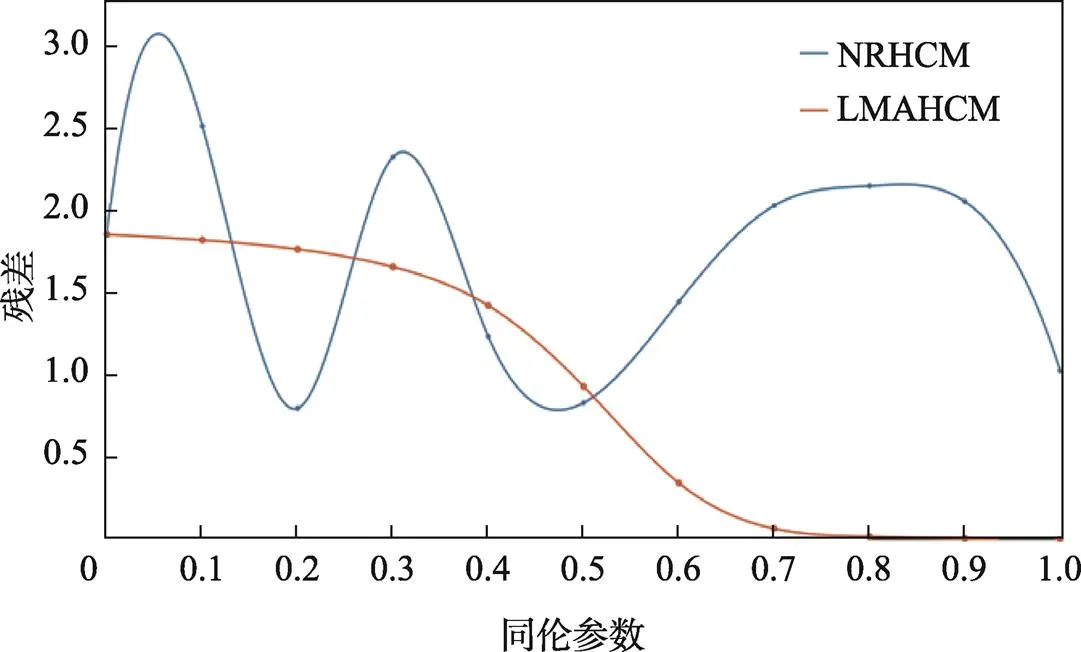
图6 奇异位姿同伦路径追踪对比
如图5所示,在非奇异位姿下,文中提出的算法LMHCM具有更好的收敛性和平滑性。如图6所示,在奇异位姿下,采用NRHCM逆运动学求解会导致发散,原因是不能计算得到雅克比的逆,而LMHCM能够保持良好的收敛效果。
4.4 机械臂搬运应用案例
在实际工程应用中,常使用机械臂搬运产品线上的产品。文中提出的逆运动学算法可以更精确地计算出机械臂抓取产品各关节的角度,进而运动到产品位置进行搬运。文中设计了一个模拟产品线上机械臂抓起搬运的任务,机械臂需要将点的产品经过点运送到点,最终回到起始位置。假设产品的位置、中间路径点及终止点的位姿信息已知,机械臂末端执行器抓取点的位姿如表4所示,位置坐标为[,,],姿态坐标采用欧拉角描述为[,,]。根据文中所提LMHCM逆运动学算法计算上述各位姿的关节角度,结果见表5。通过逆运动学计算得到3个路径点的关节角度后,在关节空间采用三次样条曲线进行轨迹规划,末端执行器运行轨迹如图7所示。经过仿真验证,机械臂能够以预定的运动精度完成待包装产品的抓取搬运工作。
表4 抓取点位姿坐标

Tab.4 Pose coordinate of grabbing point
表5 抓取点关节角度

Tab.5 Joints angles of grabbing point
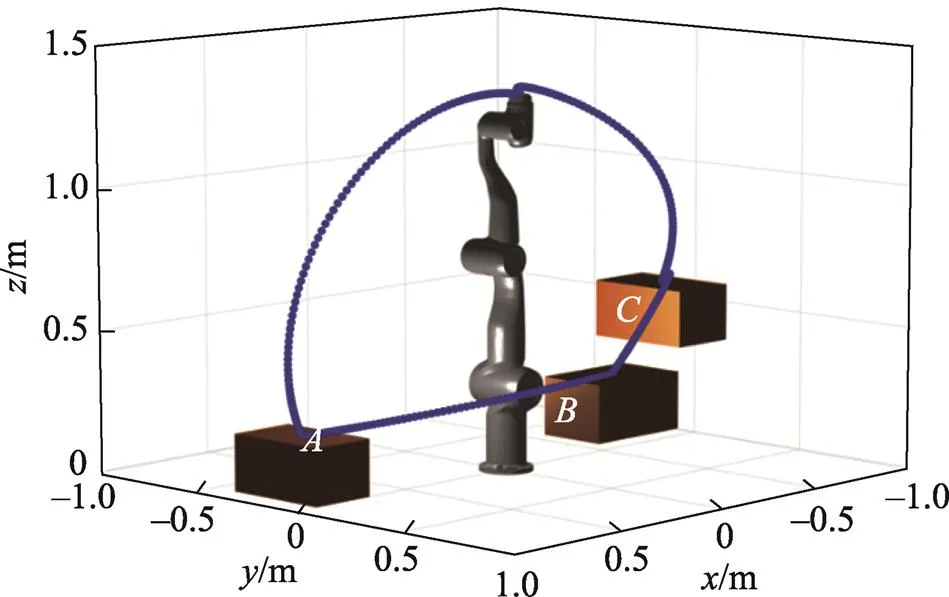
图7 末端执行器搬运轨迹
5 结语
为了获得具有自运动特性和关节极限规避的带偏置七自由度机械臂运动学逆解,提出了一种改进数值求解方法。将LM算法与HCM相结合,不仅有效避免了数值法对初始值敏感的问题,提高了数值法的鲁棒性和收敛速度,而且利用同伦延拓算法能够获取逆运动学解空间。同时,将避免关节极限映射为解空间中关节角度的最优选择问题,建立适应度函数为优化目标,利用SABPSO算法搜索出一组在关节极限内的最优关节角度。仿真验证了所提出的逆运动学求解空间方法及关节极限避免算法的正确性和可行性,对于机械臂后续用于包装作业具有一定的理论意义和工程应用价值。
[1] SHI X H, GUO Y, CHEN X C, et al. Kinematics and Singularity Analysis of a 7-DOF Redundant Manipulator[J]. Sensors, 2021, 21(21): 7257.
[2] ZHANG Q. Robotics Mechanisms, Kinematics, Dynamics and Motion Planning[J]. 2019, 15(3): 125-141.
[3] SHIMIZU M, KAKUYA H, YOON W K, et al. Analytical Inverse Kinematics for 7 DOF Redundant Manipulators with Joint Limits[J]. Journal of the Robotics Society of Japan, 2007, 25(4): 606-617.
[4] 朱经纬, 方虎生, 邵发明, 等. 自适应粒子群算法求冗余机械臂逆运动学解[J]. 计算机工程与应用, 2019, 55(14): 215-220.
ZHU Jing-wei, FANG Hu-sheng, SHAO Fa-ming, et al. Self-Adaptive Particle Swarm Optimization Algorithm for Solving Inverse Kinematics Problem of Redundant Manipulator[J]. Computer Engineering and Applications, 2019, 55(14): 215-220.
[5] 张立博, 李宇鹏, 朱德明, 等. 基于遗传算法的护理机器人逆运动学求解方法[J]. 北京航空航天大学学报, 2022, 48(10): 1925-1932.
ZHANG Li-bo, LI Yu-peng, ZHU De-ming, et al. Inverse Kinematic Solution of Nursing Robot Based on Genetic Algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(10): 1925-1932.
[6] GAO R H. Inverse Kinematics Solution of Robotics Based on Neural Network Algorithms[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(12): 6199-6209.
[7] KÖKER R. A Neuro-Simulated Annealing Approach to the Inverse Kinematics Solution of Redundant Robotic Manipulators[J]. Engineering with Computers, 2013, 29(4): 507-515.
[8] LEE S, LEE J, BANG J, et al. 7 DOF Manipulator Construction and Inverse Kinematics Calculation and Analysis Using Newton-Raphson Method[C]// 2021 18th International Conference on Ubiquitous Robots (UR). IEEE, 2021: 235-238.
[9] 房立金, 高瑞. 一般6R机器人逆运动学算法的改进[J].机械科学与技术, 2018, 37(9): 1325-1330. FANG Li-jin, GAO Rui. Improving Inverse Kinematics Algorithm for General 6-DOF Robots[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(9): 1325-1330.
[10] XIE Y E, WU X D, SHI Z, et al. The Path Planning of Space Manipulator Based on Gauss–Newton Iteration Method[J]. Advances in Mechanical Engineering, 2017, 9(8): 168781401771847.
[11] LIAO L C, CHEN W B, YAN D, et al. Solution of Inverse Kinematic Problem for Serial Robot Based on Screw Theory[C]// SPIE Smart Structures + Nondestructive Evaluation Proc SPIE 11376, Active and Passive Smart Structures and Integrated Systems XIV, 2020: 492-496.
[12] WU L, YANG X D, MIAO D J, et al. Inverse Kinematics of a Class of 7R 6-DOF Robots with Non-Spherical Wrist[C]// 2013 IEEE International Conference on Mechatronics and Automation, 2013: 69-74.
[13] ANANTHANARAYANAN H, ORDÓÑEZ R. Real- Time Inverse Kinematics of (2+1) DOF Hyper-Redundant Manipulator Arm via a Combined Numerical and Analytical Approach[J]. Mechanism and Machine Theory, 2015, 91: 209-226.
[14] SHAFIEE-ASHTIANI M, YOUSEFI-KOMA A, IRAVANIMANESH S, et al. Kinematic Analysis of a 3-UPU Parallel Robot Using the Ostrowski-Homotopy Continuation[C]// 2016 24th Iranian Conference on Electrical Engineering (ICEE), 2016: 1306-1311.
[15] LAFMEJANI A S, KALHOR A, MASOULEH M T. A New Development of Homotopy Continuation Method, Applied in Solving Nonlinear Kinematic System of Equations of Parallel Mechanisms[C]// 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), 2015: 737-742.
[16] WU T M. Solving the Nonlinear Equations by the Newton-Homotopy Continuation Method with Adjustable Auxiliary Homotopy Function[J]. Applied Mathematics and Computation, 2006, 173(1): 383-388.
[17] WU T M. A Study of Convergence on the Newton-Homotopy Continuation Method[J]. Applied Mathematics and Computation, 2005, 168(2): 1169-1174.
[18] LOVE I B. Levenberg-Marquardt Algorithm in Robotic Controls[D]. Washington: University of Washington, 2020: 10-42.
[19] BEHESHTI Z. A Time-Varying Mirrored S-Shaped Transfer Function for Binary Particle Swarm Optimization[J]. Information Sciences: an International Journal, 2020, 512(1): 1503-1542.
[20] LIEGEOIS A. Automatic Supervisory Control of the Configuration and Behavior of Multibody Mechanisms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1977, 7(12): 868-871.
Inverse Kinematics Optimization Algorithm of Redundant Manipulator Based on Homotopy Continuation
ZHANG Guoqing,LI Zongdao,WU Jianxiong,GU Haoyu,LI Qingdu*
(University of Shanghai for Science and Technology, Shanghai 200093, China)
The work aims to propose an improved numerical method to solve problems of dependence on the initial value and poor convergence of singular poses in the traditional numerical method in terms of complex inverse kinematics of the offset redundant manipulator.First, the nonlinear equations were transformed into homotopy equations. The introduction of homotopy continuation algorithm could effectively avoid the initial value dependence problem, and at the same time obtain the inverse kinematics solution space. Then taking the singular pose into account, the homotopy equations were transformed into a least squares problem, and the Levenberg Marquardt algorithm was used to track the path of the homotopy equations to obtain the inverse kinematics solution space. Finally, the joint limit avoidance problem was mapped to a solution space optimization problem, and the binary improved particle swarm optimization algorithm was introduced to obtain the optimal inverse kinematics solution. The experimental results showed that the numerical method proposed in this paper had a higher convergence rate and faster convergence speed for inverse kinematics than the traditional numerical method, and the binary improved particle swarm optimization algorithm could effectively avoid the joint limit problem. This numerical method has high accuracy in solving inverse kinematics and can meet real-time requirements, and has certain theoretical significance and engineering application value for the subsequent use of the manipulator in packaging operations.
redundant manipulator; inverse kinematics; Levenberg Marquardt; homotopy continuation; binary improved particle swarm algorithm
TP241;TB486
A
1001-3563(2024)07-0197-08
10.19554/j.cnki.1001-3563.2024.07.025
2023-07-10
国家自然科学基金(92048205)
通信作者
