基于学生核心素养培养的变式教学

张昌凤 刘琛

【摘 要】  变式教学是核心素养落地的重要途径，通过对“等边三角形”一课进行概念变式、题组变式的设计，并借助以生为本的教学环节开展落实，探讨变式教学“怎么变更合理”，从而实现培养学生核心素养这一目标.

【关键词】  核心素养；变式教学；等边三角形

1  核心素养与变式教学

义务教育数学课程标准（2022年版）指出，数学课程目标要以核心素养为导向.初中阶段侧重于对概念的理解，核心素养主要表现为：抽象能力、几何直观、推理能力、模型观念、应用意识、创新意识等，可见几何内容是培养核心素养的良好载体.而变式教学是初中数学教学尤其是几何教学的优良传统，现已积累了大量的策略方法.那么在核心素养视角下，变式教学中“怎么变更合理”这个问题为我们指出了优化变式教学的研究方向，具有深刻的理论价值和实践意义.本文以《等边三角形》为例，通过研究学情，谈谈变式教学的实践与思考.

2  教学设计分析

《等边三角形》是人教版八年级数学上册第13章《轴对称》的内容.基于学生学习了轴对称和等腰三角形有关知识，进一步探究等边三角形的性质和判定，为今后证明角相等、线段相等提供重要依据，在教材中起着承前启后的作用.

初二阶段的几何学习是培养学生几何直观、推理能力和模型观念的关键期.本课利用等腰三角形知识迁移到等边三角形的性质和判定，对学生来说有一定难度.原因在于：学生对等腰三角形“三线合一”的应用不够熟练、数学语言书写不够规范，对题目条件分析、抽离几何模型能力不强.

本课教学目标是了解等边三角形和等腰三角形的区别与联系；探索并掌握等边三角形的性质判定（难点），培养学生的探究能力和创新精神；灵活运用等边三角形的性质和判定解决几何问题（重点），发展学生的模型观念和应用意识.

3  教学过程分析

3.1  自学前诊

阅读教材P79-80例1，完成导学案（节选）.

3.1.1  回顾等腰三角形的定义、性质

定义：          是等腰三角形

性质：△ABC是等腰三角形

边：        ；角：         ；特殊线段：       ；

对称性：轴对称图形（   条对称轴）

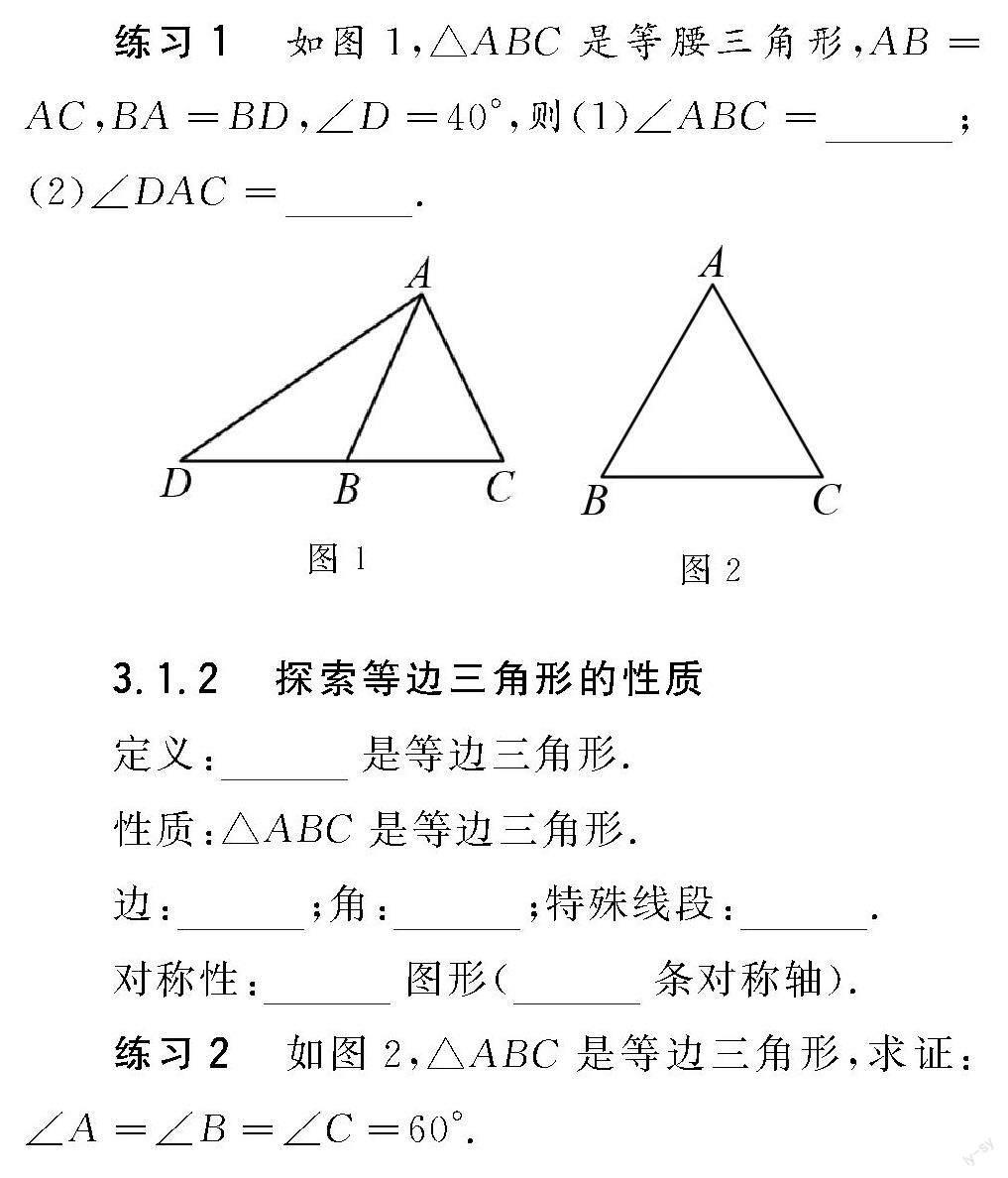
練习1  如图1，△ABC是等腰三角形，AB=AC，BA=BD，∠D=40°，则（1）∠ABC =      （2）∠DAC =

3.1.2  探索等边三角形的性质

定义：         是等边三角形

性质：△ABC是等边三角形

边：        ；角：         ；特殊线段：        ；

对称性：       图形（   条对称轴）

练习2  如图2，△ABC是等边三角形，求证：∠A=∠B=∠C=60°

证明：因为△ABC是等边三角形，所以AB=AC=BC，因为AB=AC，所以       ，因为AB=BC，所以       ，所以∠A=∠B=∠C，又因为∠A+∠B+∠C=180°，所以∠A=∠B=∠C=60°

设计意图  帮助学生回顾旧知，正向迁移得到等边三角形知识脉络，感悟对比二者的关系；以填空引导学生在证明过程中规范数学语言的表达；教师批改前诊，确定精讲内容.

3.2  引入新知、会诊答疑

展示生活中的等边三角形图片；引导学生总结等腰三角形与等边三角形的区别与联系；讲解前诊问题；引导学生探索、总结等边三角形的性质和判定（板书）.

设计意图：通过会诊，规范定理证明过程，突破难点，培养学生的逻辑推理能力；“数形结合”方式板书等边三角形的性质和判定，培养学生几何直观.

3.3  应用新知、巩固提高

例1  如图3，△ABC为等边三角形，BD=BA，求∠DAC.

练习  如图4，△ABC为等边三角形，BD、CE是AC、AB边上的中线，求∠BOC.

设计意图：学生独立思考，教师个别答疑；学生展示，教师补充.本组题目以巩固等边三角形的性质（三个角都是60°、三线合一）为主，同时渗透“外角”在解决问题时的优化作用，为后续证明做好铺垫.

3.4  合作解疑、展示风采

例2  如图5，△ABC是等边三角形，∠1=∠2 ，求证：∠ADE=60°

变式1  如图6，添加CF，使∠1=∠2=∠3，求证：△DEF是等边三角形.

变式2  如图7，擦除CF，延长AD、BD，与边BC、AC分别交于点M、N，BM=CN，（1）求证：AM = BN（2）求∠ADN度数.

变式3  如图8，延长BC、CA使得CM=AN，（1）求证：AM=BN（2）求∠ADB度数.（留作后测）

设计意图：学生独立思考、小组交流、说题板演，通过“兵教兵”实现分层教学，使每个学生得到不同的发展.例2巩固等边三角形的判定方法（三个角都相等的三角形是等边三角形）.本题组从直接利用外角得60°，到证全等得角相等，由浅入深，但易知基本图不变，多题归一，发展学生模型观念.

3.5  拓展升华、能力提升（选讲）

例3  如图9，△ABC是等边三角形，D为BC延长线上的一点，∠ACE=60°，CE=BD，（1）求证：△ABD≌△ACE；（2）试判断△ADE的形状，并证明.

变式  如图10，△ABC和△ADE是等边三角形，求证：BD=CE.（留作后测）

设计意图  本题组是两个共顶点等边三角形的旋转问题，题（1）巩固等边三角形的判定方法（有一个角是60°的等腰三角形是等边三角形）；题（2）可以利用全等性质或“8字图”模型得到∠DAE=60°，体现一题多解；培养学生规范的书写习惯，发展学生逻辑思维能力.

4  教学思考

4.1  以生为本，自主学习

本课遵循“以学生为本”的教育理念，设计了“自学、前诊、会诊、精讲、答疑、后测”六环节，为学生搭建了自主探究、思维驰骋的舞台.课前通过自学前诊的填空设问，引导学生迈小步尝试探究；课上通过会诊讲评、例题精讲、指导答疑，打开学生思维空间，巩固基本知识基本技能；既有独立思考，又有合作交流、学生展示，充分调动了学生的主观能动性.课后通过例题的变式对学生学习情况进行后测，教师根据后测情况完成反思.全程教师是组织者、引导者和合作者，而学生不断输出，成为学习的主体.这些主动学习的习惯，就是关键的品质和能力，也是学生内化的核心素养.

4.2  概念变式，纵向联系

概念教学是初中数学教学中重要的内容之一，但学生往往对概念的理解存在困难或不够深入.教师可以上下联系，设计概念的变式教学，引导学生站在知识的生长点，探究新的概念，为学生核心素养发展提供条件.比如自主研修1（等边三角形定义、性质）设置为填空题，如同提供脚手架，有助于学生独立思考；借助问题，帮助学生回归已有的认知经验，得出几何类的学习通法：定义、性质、判定；性质的研究则通常从边、角、重要线段、对称性四个方面展开.以纵向知识间的联系切入，让学生体会到知识的连贯性，促進学生构建结构化知识体系.这种类比研究的思路，是初中几何学习的重要逻辑，因此逻辑推理的素养得以体现.

4.3  题组变式，横向巩固

“双减”工作如火如荼，所以教师绝不能沉迷于题海战术，应该设计高质量的题目，浓缩数学知识的通性通法，那么题组变式就是一个很好的途径.变式训练可以使学生对知识方法的理解达到举一反三的效果，提升学生创造性的思维品质，发展学生的核心素养.设计题组变式时，要把握数学知识的本质，注重层次性，站在学生的最近发展区，并走在学生发展的前面，发挥其潜能以达到下一发展阶段水平；要将课堂上的变式延续到课后作业或阶段复习中，不断检验和夯实学生掌握的水平；也可以放手让学生摸清题目变式的门道，不断渗透图形变式、条件变式的方法：从单一到多元，从翻折、平移到旋转，从图内到图外等，切实让学生感知“解一题、会一类、通一片”的数学趣味，发展高阶思维，显著提升学生核心素养.

参考文献：

[1]教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2]邱清华.变式教学是核心素养落地的重要途径[J].数学教学通讯，2019（6）：38-39.

[3]黄信永.基于变式题组理念的教材课时整合教学：以人教版“等边三角形”为例[J].数学教学通讯，2021（2）：19-21.

[4]朱向东.立足通性通法回归数学本质：以一道等边三角形题目为例[J].山东教育，2023（1）：79-81.

[5]林立.《等边三角形》的教学设计及反思[J].中学教学参考，2020（10）：19-20.