基于犹豫模糊图的信息识别与检测∗

陈 辰

（武汉数字工程研究所 武汉 430205）

1 引言

多属性决策作为现代决策理论的重要分支，对模式识别与信息决策起到重要作用。在现实的决策环境中，决策者对信息的识别和处理存在着不完整性、不可分辨性、模糊性等，为了处理不精确与模糊信息，美国数学家、控制论专家Zadeh［1，9，16］提出了模糊逻辑和模糊集的概念，现已被广泛应用。然而，考虑到决策者认知的差异性和思维的复杂性，对相同的信息做出的决策互不相同，且难以达成一致意见。为了应对在决策时出现这种犹豫不决的状况，西班牙学者Torra［2］于2009 年首次给出了犹豫模糊集的定义，该理论的提出可以更加地反映和兼顾每一个决策者的偏好程度，更加逼近真实的决策环境，为模糊信息的识别起到了重要的作用。近年来徐泽水［5，11～15］等对犹豫模糊集作了大量研究。

模糊图的概念最早是由Rosenfeld［3］于1975 年提出，随后Rosenfeld 给出了模糊图之间的模糊关系，并且得出了模糊环境下图的一些结论。超图和模糊超图的提出为解决复杂系统中的实际问题提供了分析方法，而且图的许多应用可以推广到超图。近年来许多学者对超图的运算图做出了研究。2017 年，巩增泰等［6，8，10］讨论了模糊超图的运算图，总结了超图的计算的定义，研究了超图的运算图的性质。自犹豫模糊集问世以来，其相关理论和方法已经成为决策科学的重要研究对象。张超和李德玉［4］利用犹豫模糊集的定义，于2017年首次给出了犹豫模糊图的定义，并且通过模糊图论的一些运算性质讨论了两个犹豫模糊图的笛卡尔积，并和联等运算。2020年，巩增泰和王俊虎［7］建立了犹豫模糊超图的定义，并将其应用到信息识别与多属性决策之中。

2 预备知识

3 基于犹豫模糊超图的信息检测算法

对于模糊信息的识别在计算机工程中有着重要的作用，如何将某个方案或者计划进行选择与检测，是一个非常重要的环节。信息识别与检测过程的描述如下。

针对某一信息识别下的犹豫模糊多属性决策问题，将不同决策者对信息识别与检测的结果统计整理，并对所得到的信息进行分类融合，可对不同的方案作出不同的检测与排序，进而对各备选方案作出最佳选择。

下面我们给出一个利用犹豫模糊超图对信息识别与检测的算法。

step 1 将决策者对不同方案的评判值进行整合，得到一个关于评判值的犹豫模糊信息矩阵，并将矩阵中的数据进行分类与整合。

step 2 将所得矩阵与犹豫模糊超图相结合，并绘制出与之相符合的犹豫模糊超图模型。

step 3 根据每个方案ui的评判信息，计算出每个方案中各属性ai的得分函数。

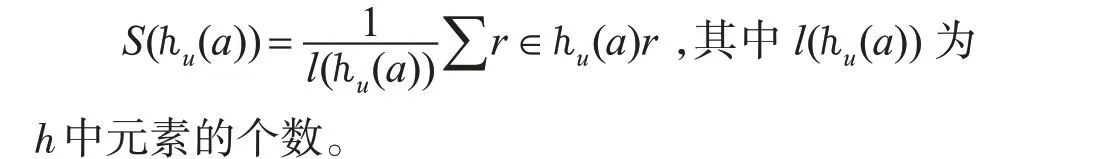
step 4 将所有方案中的相同属性整合到一起，构成一个杻。用step 3 中得到的得分函数值给λi，用λi得到的超图模型，得出检测的属性ai。

step 5 在得到的不同的属性图中，找出每个方案达到检测的属性个数并且排序，来完成对信息的识别与检测，得到最佳方案。

4 实例分析

某企业董事会决定对接下来的五年进行规划，请3 位专家对4 个规划方案u1，u2，u3，u4基于5 个不同属性a1为商业前景，a2为财务支出，a3为顾客满意度，a4为成长前景，a5为企业效益进行评估。由于3位专家来自不同的领域，做出的评估信息也各不相同，也可能未作出评判其评判信息矩阵（见表1）。

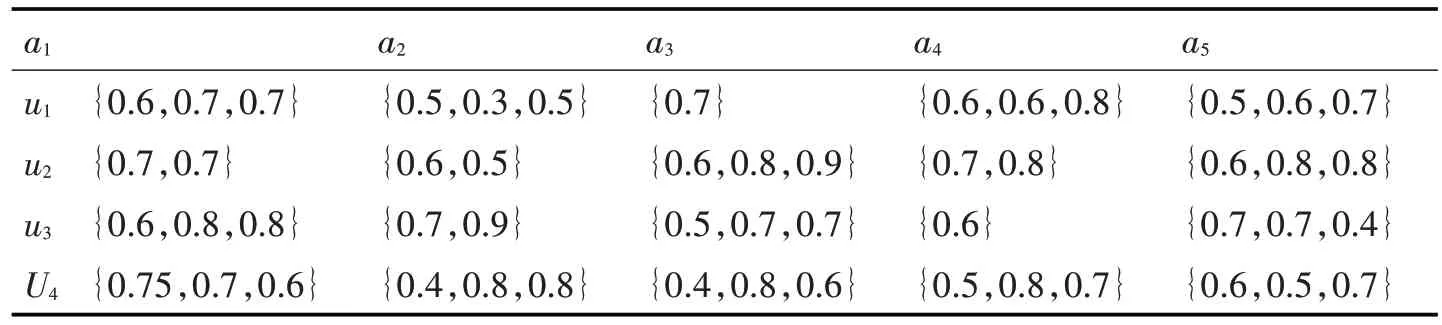
表1 犹豫模糊评判矩阵

step 1 关于决策者对方案的识别信息如表1。计算出每个方案中属性的得分函数如下：

step 2 将评判信息矩阵与犹豫模糊超图结合，得到关于属性的犹豫模糊超图模型。

step 3分别计算出每个属性的得分函数。

step 4将得到的得分函数分别值给λ，则有

λ1=0.695，λ2=0.62，λ3=0.67，λ4=0.68，λ5=0.63。

通过对得出的犹豫模糊超图模型进行计算与分割，可知达到属性a1意度的方案为u1，u2。达到属性a2 意度的方案为u3，u4。达到属性a3意度的方案为u1，u3。达到属性a4 意度的方案为u1，u2，a4。达到属性a5意度的方案为u2。

用每一个λi去得到的犹豫模糊超图模型，可以得出不同的图如下：

step 5每个方案达到检测的属性个数分别为：

方案u1有3个，方案u2有2个，方案u3有3个，方案u4有2个，对于方案u1和方案u3，

因为Su2(ai)≥Su4(ai)，则方案u2优于u4

最终各个备选方案的排序为：u3>u1>u2>u4。

5 结语

本文在已有知识的基础上，利用犹豫模糊超图和粒计算，对模糊信息进行检测，得出了一个关于模糊信息识别及其最佳方案排序的算法，并利用算例说明了该算法的可行性。 与此同时，针对属性中带有权重的相关内容，用超图解决将是我们今后的一个重要研究方向。