支持热力图等级偏好的路径规划算法∗
2024-04-17孙焕良马晓慧王亚星刘俊岭
孙焕良 马晓慧 王亚星 刘俊岭
(1.沈阳建筑大学计算机科学与工程学院 沈阳 110168)
(2.辽宁省城市建设大数据管理与分析重点实验室 沈阳 110168)
(3.国家特种计算机工程技术研究中心沈阳分中心 沈阳 110168)
1 引言
基于位置的服务广泛应用于人们的日常生活,路径规划作为基于位置的服务的基本功能之一,通常为用户提供出行的路线参考。从起点到终点的最短路径查询在路径规划中得到大规模应用[3~11]。然而,在实际生活中,人们对路径查询提出了越来越多样化的需求,例如,寻找风景优美的路径[12~13]、安全性高的路径[14~15]、感觉愉快的路径[18]等。
热力图是以不同的颜色直观地反映数据分布、密度以及变化状况的一种图示,不同颜色对应不同的数据区间,使复杂的数据清晰化。近年来,热力图在诸多领域已具有广泛的应用。城市人群热力图以颜色冷暖来反映不同地理区域内的人群密集程度,颜色越暖表示人群越密集,空气质量热力图能够精确地反映各个区域内的空气质量状况。
病毒流行期间,为避开人群保护自身免受感染,用户希望能够查询到一条人群密度小的路径。用户外出时对空气质量格外关注,通常希望得到一条途经空气质量良好区域的路径。以上需求不同于传统的从起点到终点的最短路径查询,本文提出一种支持热力图等级偏好的路径规划问题。给定一片热力图,一个起点和一个终点,给定一个路径成本预算,规划出一条从起点到终点的路径,该路径花费的成本代价不超过给定的路径成本预算,且某种热力图等级偏好的路段(称为危险路段)长度最小化。
图1 呈现了支持热力图等级偏好的路径查询问题的实例。图中的3条路径均以s为起点,d为终点。从图中可以清晰地发现,路径r1穿过的大部分区域为热力等级最高的红色;路径r2为起点和终点之间路径成本最低的最短路径;路径r3途径的大部分区域为热力等级低的紫色、绿色和蓝色。当用户倾向于经过人流密集的区域时,通常会选择热力等级高的路径r1,反之选择热力等级低的路径r3。路径r1和r3会使用户付出更多的成本代价,当超过用户的预期代价后,通常会选择最短路径r2。

图1 支持热力图等级偏好的路径规划
本文提出的支持热力图等级偏好的路径规划是一种新的路径规划问题。传统的路径规划通常侧重于寻找行程距离或时间最短的路径,如文献[3~6]提出了基于索引的有效处理最短路径查询的方法。还有一部分路径规划问题考虑了用户偏好,文献[12]提出一种算法ILS*(C),同时考虑弧的成本和值,查询得到一条风景得分最高且不超过总旅行成本的路径,文献[14]在未给定旅游成本的情况下,设计算法旨在输出一组路径,在距离和安全性之间做出权衡。以上相关研究最大化路径的效益值,最小化路径成本。与上述研究不同,本文的研究目标是在路径成本预算范围内最小化危险路段长度。
本文所提出的路径规划问题主要涉及热力图数据,数据分布具有不规则性和多样性,如何对热力图数据进行有效的组织,以及如何设计有效的算法在路径成本预算内减少路径中危险路段的长度是本文面临的挑战。本文在对热力图数据进行处理时,采用基于网格的索引,一个网格与一个热力等级相对应。根据热力图中热力等级的实际分布,对危险区域进行预处理,提出一种热力等级最小区域边界矩形生成处理方法。基于A*算法的思想,提出一种两阶段危险网格替换算法。由于该算法需遍历大量网格,为简化路径查询方式,在热力等级最小区域边界矩形生成算法的基础上提出一种基于危险区域规避图路径查询算法。
本文的主要贡献如下:
1)定义了一种新的路径规划问题,即支持热力图等级偏好的路径规划。
2)在欧式空间内,提出了基于危险网格替换的A*算法,以减少危险网格的个数。提出了一种基于危险区域规避图路径查询算法,简化路径搜索的方式,以减少路径搜索过程中的时间和空间代价。
3)实验在真实的热力图数据集上进行,以危险路径的长度、算法运行时间等为指标验证所提算法的有效性。
2 相关工作
2.1 最短路径查询
作为在线地图应用中的基本操作,最短路径查询的高效处理得到了广泛的研究。最基本的算法包括Dijkstra和A*算法,A*算法是一种经典的最短路径搜索方法[1~2]。由于它们在没有任何辅助索引的情况下搜索空间,查询效率不够高效。基于索引的算法能够显著提高查询性能,例如收缩层次结构(Contraction Hierarchy,CH)[3~4]、Hub 标签(Hub Labeling,HL)[5~6]等。
在高度动态的环境中,使用批处理最短路径算法,无需索引结构,在多个查询之间共享计算[7~8]。文献[9]将动态网络视为快照序列,对它们进行聚集,选择一些作为典型快照并为其建立索引。维护索引的算法在路网发生变化时,直接刷新索引,文献[10]使用压缩层次结构作为底层最短路径计算方法,文献[11]采用基于树分解的Hub标签作为底层索引。
本文提出的路径查询并非计算最短路径,而是基于热力图数据,将热力图划分为若干大小相等的网格,根据每一个网格对应的热力等级划分为安全网格和危险网格,寻找经过危险网格长度最小化的路径。
2.2 偏好路径查询
除了最短路径查询,近年来偏好路径查询也得到了诸多研究,以满足用户对路径查询的多样化需求。大多数偏好路径查询问题可以被描述为弧定向问题(Arc Orienteering Problem,AOP),应用包括找到最佳风景的路径[12~13,20~22]、安全的路径[14~15,23]和感觉快乐的路径[18]等。
AOP问题是NP难题,为了解决这个难题,常见的方法是在路线上设置各种约束,使寻找的解决方案尽可能接近最优解。文献[16]对个性化多样性需求建模,并使用用户偏好和约束修剪搜索空间的策略,提出了top-k 路线搜索问题的最优解,文献[17]为确保路线的风景质量,对必看的景点做出限制。除此之外,文献[19]提出分支切割方法和迭代局部搜索算法,来解决骑行规划AOP 问题的变体。文献[20~21]提出行驶时间和值双重时间依赖的AOP 问题,文献[20]中的算法仅提高单条最快路径的质量,而文献[21]中的算法基于初始路径群提高解决方案的质量。
本文提出的路径规划是一种典型的偏好路径查询,在有限的路径成本预算下,查询到一条危险路段长度最小化的路径。本文的研究是在热力图等级约束中进行,结合热力图的分布特点进行路径规划。
3 问题定义
定义1(热力等级)热力等级θ代表了在一定范围内某种特征密集程度,利用1,2,…,n 表示,其中1为最低级,n为最高级。
在城市人群热力图中,七种不同的颜色对应七种不同的热力等级,从小到大依次为灰色、紫色、蓝色、绿色、黄色、橙色、红色。最低等级为1 级对应灰色,代表该区域人群密度最低,最高等级为7 级对应红色,代表该区域内人群最密集。
定义2(带有网格结构的热力图)给定一片热力图,将其划分为若干个大小相等的网格,网格结构的热力图表示为H。每一个网格g∈H 均为正方形,表示为(x,y,θ),x 和y 分别表示该网格位置的横纵坐标编号,θ表示该网格的热力等级,网格g 的边长表示为g.l。
如果路径经过一个危险网格g,g 的危险长度取正方形对角线长度 2 l,表示为g.risk,非危险网格长度为0。热力图数据分布具有不规则性,当一个网格内出现多个不同热力等级时,采用近似处理方式,将网格中的最高热力等级设置为该网格所对应的热力等级。
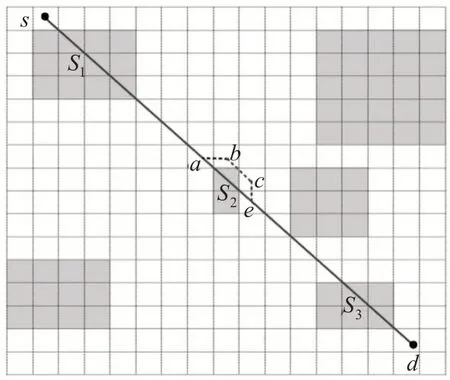
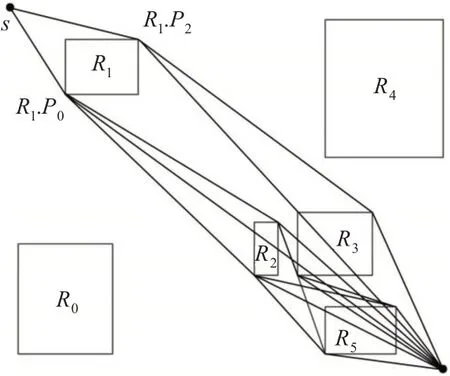
定义3(支持热力图等级偏好的路径规划)基于带有网格结构的热力图H,给定起点s,终点d,路径成本预算B。支持热力图等级偏好的路径规划Q(s,d,B,k)返回一条路径成本代价l 不超过路径成本预算B,且经过热力等级大于等于k级(1 支持热力图等级偏好的路径规划问题需要同时满足两个约束条件,一是路径花费的成本代价小于给定的路径成本预算B,二是路径S 中危险区域的长度小于任何其他同时满足两个约束条件的路径Sn,约束条件表示如式(2)所示。 图2 为查询示例。给定带有网格结构的热力图,s 为起点,d 为终点,成本预算B 为24,带有颜色的网格为危险网格。假设向上、下、左、右四个方向寻路,相邻网格之间移动的代价为1,向左上、左下、右上、右下四个方向寻路,相邻网格之间移动的代价为1.4。满足约束条件的情况下,查询路径为s-a-b-c-d,即图中用黑虚线表示的路径。 图2 支持热力图等级偏好的路径规划示例 下面分析支持热力图等级偏好的路径规划问题的查询代价。假定每个网格的出度为μ,即经过该网格后有μ种选择,在路径成本预算约束下可通过的网格个数为τ,则代价为μτ,支持热力图等级偏好的路径规划问题是NP难问题。 基于A*算法的思想,本文提出一种两阶段的危险网格替换算法。算法由求解最短路径和危险网格替换优化两部分组成,第一阶段,以起终点之间的最短路径作为初始解;第二阶段,对初始解中包含的危险网格进行替换,从而查询到一条满足路径成本预算,且经过危险路段长度最小化的路径。 如算法1 所示:使用A*算法搜索得到从起点s到终点d的最短路径作为初始解(第1行)。找到初始解中热力等级大于等于k 的网格,将其中相邻的部分合并(第2 行)。合并后的每一段危险网格记为Si,危险路段的个数为count,优化阶段分别进行替换。再一次使用A*算法,得到危险路段的替换路径Se(第3 行~4 行)。对替换路径Se是否满足条件进行判断,如果替换路径中无热力等级大于等于k 的网格,并且替换后路径成本花费小于路径成本预算B,则将会降低路径中危险网格的个数,对危险路段进行替换,更新路径S。若不满足其中的任意一个条件,则意味着路径替换失败,不进行路径的更新,保留路径S 中的危险网格(第5 行~8 行)。将每一段的危险路段都遍历完成后,得到优化后的路径S并返回(第9行)。 算法1 基于危险网格替换的A*算法 图3为算法1的示例,路径成本花费B为22,其他条件同上节。第一阶段得到初始解s-a-e-d,即从s 到d 的最短路径。其中,S1、S2和S3为需要替换的危险路段,根据替换条件,只有路径a-b-c-e 对a-S2-e 的替换有效,初始路径被更新为s-a-b-c-e-d。更新后的路径缩短了危险路段的长度,且路径花费不超过B。 图3 基于危险网格替换的A*算法示例 基于危险网格替换的A*算法,初始解中热力等级大于等于k 的网格将会被替换掉且更新后的路径围绕在初始解周围,以保证更新后的路径满足路径成本预算。但是,如果初始解中包含较多的危险网格,将进行多次的危险网格替换,必然会增加时间和空间成本。如果初始解中危险网格周围围绕着诸多危险网格,则不满足路径中危险路段长度最小化的需求,路径替换失败,导致初始解中危险网格的替换具有局限性。 算法的时间复杂度分析如下,A*算法的平均时间复杂度为O(NlogN)(N为问题规模),本节提出的算法基于A*算法的思想,第一阶段计算最短路径,第二阶段对最短路径中的危险网格进行替换,均采用A*算法,因此基于危险网格替换的A*算法的时间复杂度将高于A*算法。 上节提出了一种基于危险网格替换的A*算法,在查询过程中,当网络的数据量较大时,查询算法效率无法支持在线系统应用。为了提高查询效率,本文提出了一种基于危险区域规避图路径查询算法。通过将热力图中的危险区域近似成矩形结构,生成最大化避开矩形结构的危险区域规避图,从而查询出一条不超过路径成本预算B 且经过危险区域长度最短的路径。 定义4(热力等级最小区域边界矩形)基于带有网格结构的热力图,将热力等级大于等于k 级(1 < k ≤n,n 为最大热力等级)的危险区域用最小外接矩形包围起来,生成热力等级最小区域边界矩形(Thermal level minimum region boundary rectangle,TMBR)。其范围由矩形的四个顶点表示,即R.P0、R.P1、R.P2、R.P3。 在热力图中,由于热力等级分布具有分散性,生成多个TMBR,TMBR 的集合记为R。下文中,将每个TMBR 记为Ri,i 的值从0 开始,为根据纵向位置排序TMBR的序号。 本节所提算法的查询过程如算法2 所示:根据热力图中热力等级的分布情况,调用算法3 createMBR(k,H),对危险区域做近似处理,生成TMBR(第1 行)。为避开危险区域,在生成的TMBR 基础上,调用算法4 evadeGraph(s,d,R),在线生成用于路径查询的危险区域规避图G(第2行)。在图G中调用A*算法(第3行),最终返回满足两个约束条件的路径S(第4行~5行)。算法生成边界矩形过程可以在查询执行前进行,当查询到来时在线生成规避图,然后进行路径查询。 算法2 基于危险区域规避图路径查询算法 4.2.1 热力等级最小区域边界矩形生成算法 根据热力图中不同热力等级区域的实际分布情况,本文在网格索引的基础上,使用最小边界矩形,将危险区域近似成矩形结构,生成热力等级最小区域边界矩形TMBR。 生成每一个TMBR 需要不断合并扩展,如算法3 createMBR(k,H)所示。当一个未合并的危险网格h 存在时,设置变量up、down、left、right 分别表示危险网格向上、下、左、右四个方向拓展的距离。当危险网格上方为危险网格时,up将向上移动一个单位,即up-1,并将(up,left)、(up,right)范围内的网格合并;反之,则不进行合并,变量的值不变(第1行~4 行)。在对下、左、右三个方向进行合并判断时同理(第5行~13行)。当危险区域的四周均不存在危险网格时,四个变量值均已更新完成,确定TMBR的范围并返回(第14行~15行)。 算法3 createMBR(k,H) 4.2.2 危险区域规避图生成算法 危险区域规避图是根据一定的判断规则在路径起终点与TMBR 之间形成的,由诸多有效边和有效顶点组成。每一条有效边需要同时满足三个条件:第一,当前顶点同TMBR 的顶点之间的连线不经过任何危险区域;第二,TMBR 的顶点同终点之间的连线经过的危险区域长度小于连接当前顶点同终点的直线之间经过的危险区域长度;第三,TMBR 的顶点同终点之间的连线不经过自身所在矩形。同时满足三个条件后,则当前顶点为有效顶点,即下一次寻找有效边的新起点。路径查询在图上进行,不仅简化了查询方式节约时间和空间成本,而且能够尽可能地避开危险区域,满足用户偏好。 危险区域规避图生成过程如算法4 evade-Graph(s,d,R)所示,初始化存储顶点的队列qv和存储有效边的队列qe,起点s 添加进入qv(第1 行~2行)。当队列不为空时,当前顶点为qv中首元素,并使用变量count 记录起终点之间经过的第一个TMBR 的序号(第3 行~4 行)。若当前顶点同终点之间经过危险区域,将当前顶点与第一个经过的TMBR的四个顶点依次相连,根据上述三条判断规则,满足条件的边加入qe,顶点加入qv,若当前顶点不是起点s,则将当前顶点同终点创建的边加入qe(第5行~11 行)。若当前顶点同终点之间不经过任何危险区域,则直接连接两顶点构建的边(第12行~13行)。直至所有有效边创建完成,返回图G(第14行)。 算法4 evadeGraph(s,d,R) 危险区域规避图的创建过程如图4 所示:起点s和终点d所连接的边经过的第一个TMBR为R1,将s 依次与R1的四个顶点相连寻找有效边。边 图4 危险区域规避图生成示例 危险区域规避图中的边具有两个重要特点:第一,位于两个不同TMBR 的顶点创建的边一定为安全边,没有经过任何一个危险矩形;第二,当前顶点与终点d 创建的边可能既有安全边,也有危险边,且危险边长度一定小于起终点路径中危险路段的长度。这种特点大大地降低了危险边的数量和长度,使得路径查询时可以尽可能地避开危险路段。 上一节提出的算法在网格上进行,返回的路径由诸多网格构成,本节提出的算法在危险区域规避图上进行,返回的路径由边构成,简化了路径查询的方式。基于危险区域规避图进行路径查询过滤掉大量危险边,对比算法示例可以发现,图4 中有效边和有效顶点的数量远少于图3 中网格的数量,当网络数量为N 时时间复杂度将小于O(NlogN),减少了时间和空间成本,提升了算法的执行效率。 本节利用真实的热力图数据集对所提算法进行实验测试,对比分析不同算法的实验结果。 热力图数据采集自百度城市热力图平台,本文实验采用北京市2021 年3 月份的数据,每10min 采集一次,共采集到4120 张,采集到的数据量能够验证本文所提算法的有效性。热力图数据进行网格化处理后,包含网格位置的横坐标编号x、纵坐标编号y 和网格位置的热力等级等属性,数据样例如表1所示。 表1 实验数据集样例 根据人群密集程度将热力图中的热力等级划分为7 级,从1 级到7 级,热力等级逐级升高,人群密集程度逐渐增加。本节定义的危险等级为7 级,危险区域为热力等级为7级的区域。 针对支持热力图等级偏好的路径规划问题,本文设计实现了基于危险网格替换的A*Grid 算法和基于危险区域规避图路径查询算法avoidGraph。由于现有相关工作中没有基于热力图进行支持热力图等级偏好的路径查询算法,因此本文将A*算法和采用文献[12]替换思想设计的算法A*Grid 算法作为对比算法。 本节分别基于带有不同网格粒度和不同起终点欧式距离的热力图对算法的查询精度进行比较。各个测试中,路径长度单位(即路径成本)为200*200 粒度网格中每一个网格的边长。采集同一时刻下同一区域内的热力图,分别添加200*200、100*100、50*50 大小的网格结构,起终点欧式距离设置为3km,测试不同网格粒度对算法查询精度的影响。欧式距离分别取3km、6km、9km、12km和15km,选择网格粒度为200*200 的热力图,测试不同起终点欧式距离对算法查询精度的影响。为了更准确地比较各个算法的查询精度,实验分别运行10次,取其平均值作为最终结果。 图5(a)和图5(b)分别展示了不同网格粒度下和不同起终点欧式距离下危险路径长度的变化情况。以A*算法计算的起终点之间最短路径经过的危险路段长度为对比,从图中可以看出优化后的路径中危险路段的长度均不大于初始路径中危险路段的长度,这是因为avoidGraph算法和A*Grid算法均在给定的路径成本预算范围内,多付出一些路径成本避开危险区域。avoidGraph 算法优化后的路径经过的危险区域长度最短,因为在危险区域规避图的创建过程中,过滤掉了大量经过危险区域的无效边,仅保留安全边或危险长度短的有效边。使用A*Grid算法优化后的路径,危险路径长度变短但危险路段依旧存在,因为路径规划过程中存在两种可能性,第一种可能是危险网格周围分布着大量危险网格,导致无法进行网格的替换;另一种可能是替换路段后路径成本花费超过给定的路径成本预算,为了控制路径成本,不得不选择一条经过危险区域的路径。 图5 不同约束条件对危险路段长度的影响 如图5(a)所示:A*算法计算的最短路径中,随着粒度变粗危险路段的长度呈现上升趋势。这是因为粗网格粒度代表近似的计算,当网格粒度从200*200 变为100*100、50*50 的过程中,一些安全区域被近似计算为危险区域,扩大了危险区域的范围,导致危险路段的长度增加。如图5(b)所示:随着起终点之间欧式距离的增加,A*算法计算的起终点最短路径中危险路段的长度增加,因为起终点之间距离越长,经过危险路段的可能性越高。需要说明的是路径中危险路段的长度与起终点之间危险区域的分布有关,与起终点之间欧式距离的长度不成比例关系。 图6(a)测试了网格粒度对路径成本的影响,网格粒度越大查询安全路径所花费的成本越高,与图5 中危险路段的长度呈现相同的变化趋势。图6(b)比较了路径成本随起终点欧式距离的变化情况,以A*算法计算出的最短路径成本代价为对比,图中可以看出,随着欧式距离的增加,路径查询所需要的代价随之增加。当欧式距离或网格粒度相同时,A*Grid算法查询到的优化路径所需的成本明显要高于avoidGraph 算法所需的成本,这是由于A*Grid算法是沿着网格进行寻路,路径只能沿着特定方向进行,而avoidGraph 算法在生成的危险区域规避图上进行寻路,路径搜索本质上是沿欧氏距离进行的,而且前者搜索路径的次数比后者要多,因此前者消耗的成本要明显多于后者。 图6 不同约束条件对路径成本的影响 本节分别测试在不同网格粒度和起终点欧氏距离下,A*算法、A*Grid 算法以及avoidGraph 算法运行10000次路径查询所需时间,其他条件同上节。 图7(a)展示了热力图网格粒度对于算法效率的影响。相同网格粒度下,avoidGraph 算法运行效率最高,A*Grid 算法运行效率最低;网格粒度由细到粗变化时,算法运行消耗时间大幅下降。图7(b)展示了算法运行效率随起终点欧式距离的变化情况。欧式距离相同时,avoidGraph 算法查询效率最高,A*Grid算法查询效率最低;对于同一种算法,欧式距离的增加时,算法查询所需时间增加。特别当欧式距离大于9km 时,A*Grid 算法和A*算法的运行时间增长较快。原因是avoidGraph 算法路径规划在图上进行,而A*Grid 算法和A*算法在网格中进行,图中顶点和边的数目远小于网格的数量;A*Grid 算法是一种两阶段算法,在使用A*算法获取最短路径后,需对路径中的危险网格进行替换,因此时间效率最低。 图7 不同约束条件对算法效率的影响 本文提出一种支持热力图等级偏好的路径规划问题。设计了两种查询优化算法,包括基于危险网格替换的A*算法和基于危险区域规避图的路径查询算法。利用真实的数据集进行了充足的实验,验证所提出算法的有效性。 由于热力图是实时更新的,在未来的工作中可以根据获得的热力图数据,进行热力图模式发现,形成在时间和空间上相近规律的生成模式。根据用户选择的不同的出行方式,即步行、骑行和驾驶,可以确定用户的预计到达时间。根据给定的出发时间、起点和终点确定相应的热力图模式。初始查询在单片图上进行,若在用户未到达终点时间内,区域的热力图模式发生变化,则把相应的模式引入,在新的热力图模式上进行后续的查询。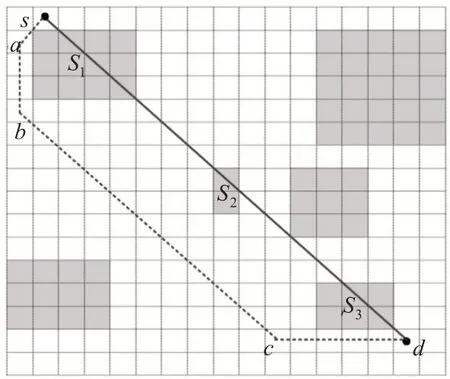
4 查询处理
4.1 基于危险网格替换的A*算法

4.2 基于危险区域规避图路径查询算法



5 实验分析

5.1 算法的精度比较


5.2 算法的效率比较

6 结语
