气云爆炸下波纹板结构特征对抗爆性能影响研究*

李均海

(1.化学品安全全国重点实验室,山东青岛 266104 2.中石化安全工程研究院有限公司,山东青岛 266104)

0 前言

在化工园区、海洋平台等工业生产区域,存在着爆炸的潜在风险,如储油罐、油气介质存储装置等。在面对这些危险源的时候,除从本源上进行安全处置,往往还需设置抗爆结构,如抗爆墙、庇护所等,将危险源与工作人员、控制室等分隔开,以降低危险性。波纹板因其轻质高强度、高稳定性的特点,在抵抗破片冲击、削弱冲击波能量等方面有着优越的表现,被作为抗爆结构广泛应用于安全防护中[1-4]。

近年来,许多国内外学者通过理论推导、试验、数值模拟等方式对波纹板在爆炸荷载下的响应特性及影响因素进行了深入研究,取得了诸多成果。LUO R,等[1]采用ABAQUS研究了波纹板几何尺寸、加载及边界条件对其性能的影响,得出波折角对波纹板屈曲模式影响显著。JUNG MS,等[2]对比分析了加强筋波纹板与普通波纹板在荷载下的动态响应过程及变形,发现加强筋波纹板可以吸收更多应变能及延迟屈曲发生时间。MAGNUCKA-BLANDZI E,等[3]基于Hamilton准则推导了波纹板在静荷载下的运动方程,得出可以通过改变波纹板几何形状及其厚度来调整其性能。LUO F,等[5]基于数值非线性动力方法,对常规钢波纹防爆墙、再入式防爆墙、蜂窝夹层防爆墙等进行了爆炸模拟,并分析其动态响应过程。李永正,等[4]使用MSC.Dytran模拟了传统平板、波纹板、夹层板等多种结构的燃油舱舱壁在爆炸荷载下的吸能情况,得出波纹板结构具有很好的抗爆效果,且波纹板截面高度较小时效果最佳。师吉浩,等[6,7]基于非线性有限元分析方法,分析了3种结构形式的波纹板防爆墙,采用P-I模型进行曲线参数影响分析,建立了任意截面尺寸的防爆墙P-I曲线预测经验公式。王锐,等[8]采用非线性有限元方法对比了动态算法与准静态算法的适用性,分析了波纹板在荷载冲击下结构应变的3种形式。纵观以上研究,各学者从机理上对波纹板在爆炸荷载下的防护性能进行了分析研究,但鲜有作者分析研究气云爆炸荷载下波纹板结构参数对其抗爆性能的影响规律以及各因素影响程度。

本文拟采用ABAQUS软件建立有限元模型,并搭建试验平台模拟气云爆炸验证模型准确性,基于波纹板特征分析各因素对其防护性能的影响,结合正交试验法分析得出各因素对波纹板抗爆性能影响程度。

1 有限元模型

1.1 模型建立

利用有限元仿真分析软件ABAQUS/Explicit建立波纹板、框架的有限元模型,采用软件的动力显示分析模块模拟爆炸时冲击波对波纹板的冲击作用。波纹板截面通常分为2种类型,弧形结构与梯形结构。目前在抗爆庇护所等结构中,采用梯形结构较为广泛,因此本文以梯形结构为研究对象,梯形截面如图1所示,参数包含厚度t、波宽L1、坡宽L2、坡深h。

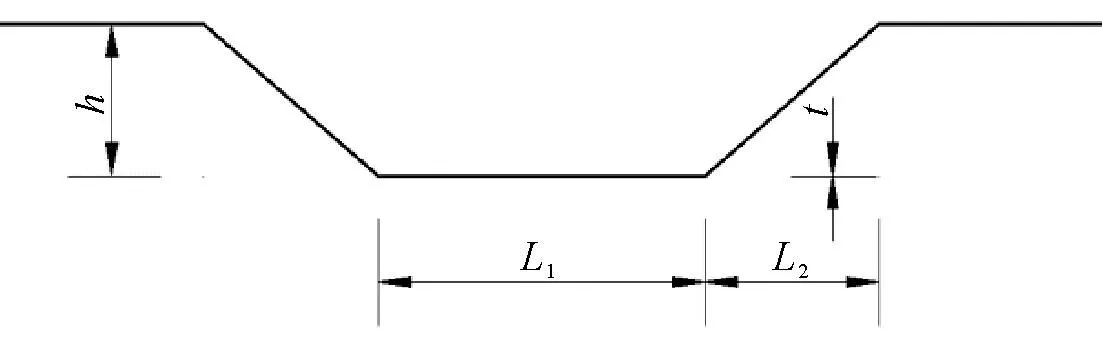
图1 波纹板截面示意

模型中波纹板采用Q235B钢,厚度3 mm,尺寸为2 400 mm×1 200 mm;框架采用截面尺寸为外径50 mm、内径40 mm的Q235B空心方钢,边框尺寸为2 450 mm×1 250 mm,中间设置一道横梁。模型对框架采用完全固定的边界条件,并将波纹板及框架二者间接触设置为绑定约束,以实现框架对波纹板的固定作用。在网格划分时,为避免畸变单元的产生,沿方钢内外径对框架整体进行了切分,然后对框架和波纹板采用C3D8R减缩积分单元进行划分,网格尺寸均为1 mm,二者的建模及网格划分见图2。

图2 模型及网格划分示意

1.2 材料本构模型

由于在爆炸冲击过程中,波纹板处于高应变率、大变形的环境下,受到高压的影响,因此文中Q235B钢采用了Johnson-Cook模型定义其本构关系,该模型考虑了材料的应变硬化、应变率强化,其表达式见式(1)[9]:

(1)

式中:σ——动态屈服应力,Pa;

A——静态屈服应力,Pa;

B——应变硬化参数,Pa;

εp——屈服应变;

n——硬化指数;

C——应变率相关系数;

m——温度相关系数;

T*——相对温度。

材料发生断裂时,应变表达公式见式(2)。

(2)

式中:εf——断裂应变;

D1,D2,D3,D4,D5——材料参数;

σ*——三轴压应力,Pa。

Q235B钢材的基础参数及相应的Johnson-Cook模型参数列于表1。

表1 Q235B钢本构模型参数[10]

1.3 CONWEP爆炸控制方程

有限元模拟爆炸荷载有3种主流方法——ALE流固耦合算法、CONWEP法、荷载时程曲线加载。ALE流固耦合算法通过创建结构、空气、炸药模型,可以较为真实地模拟出空气介质对结构冲击的过程,但模型构建复杂,计算量大,计算速度慢;荷载时程曲线加载是根据爆炸过程中检测到的爆炸超压及作用时间,对结构施加荷载时程曲线,对数据精度要求高,且难以还原真实场景;CONWEP法是美国军方开发的爆炸荷载模拟方法,其在模拟空气域中爆炸时所具有的优势在于忽略了空气介质的惯性及刚度,可减少建模步骤,计算量小,精确度能达到研究要求,通过给定TNT当量和起爆点,便可计算出冲击波传播至承载面的时间、最大超压及指数衰减因子等参数。本文采用CONWEP法进行模拟,其在无限空气中的函数关系式见式(3)[11]:

Δp=f(E0,p0,ρ0,r)

(3)

式中:Δp——爆炸超压,MPa;

E0——炸药能量,J;

p0——空气初始状态压力,MPa;

ρ0——空气密度,g/cm3;

r——起爆点至承载面的距离,mm。

(4)

式中:ω——装药量,kg;

0,1,…,n——函数幂级数展开次数;

A0,A1,…,An——无量纲系数,由实验环境决定。

经多次修正,在ABAQUS中对于指定爆炸点、TNT当量、爆炸承载面,CONWEP表达式见式(5)。

(5)

式中:p(t)——爆炸承载面上任意点压强,MPa;

pincident(t)——入射波压强,MPa;

preflect(t)——反射波压强,MPa;

θ——入射角,°。

2 实验设计与模型验证

2.1 实验装置与方法

为保证实验的准确性和可靠性,本实验装置由4部分组成——配气系统、爆轰装置、抗爆框架、测试板,为实验提供稳定的气源、爆源和足够刚度的约束装置,其结构如图3所示。试验时采用气体爆轰的方式模拟气云爆炸对测试板产生的冲击,实验采用了自研的配气系统,突破了大流量配气与高效混气等关键技术,氧含量分析仪采用了西门子 oxymat 6,其精度为小于当前测量量程的1%,可以为实验提供“4.2%的丙烷+空气”的稳定气体介质。爆轰装置是由一根长管道与扩口连接而成,管道长36 m,直径为500 mm,扩口尺寸为2 000 mm×2 000 mm,可为实验提供稳定的爆轰过程。抗爆框架用于固定测试板,通过碳钢焊接成型,框架中心部位设有专门安置测试面板的金属龙骨,总重超1 400 kg,具有优异的抗爆性能及结构强度,可以为测试板提供足够刚度的约束。其结构如图4所示。测试板采用了厚度为3 mm的Q235B钢板,尺寸为1 200 mm×2 400 mm。

图3 实验装置示意

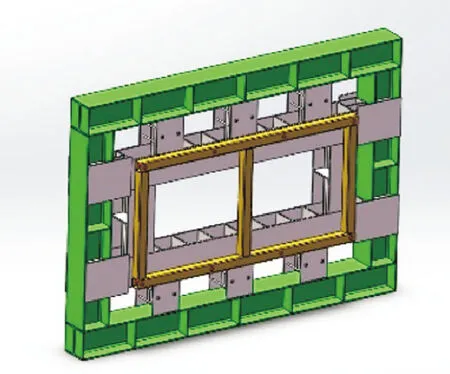
图4 抗爆框架示意

2.2 模型验证

为了验证数值模型的有效性,开展了2组平面板受气云爆炸冲击的试验,如图5(a)所示。图5(b)为实验后的平面板变形图,两组试验变形模式基本一致,由四周向两侧中心处凹陷;通过激光测距仪分别对每组两侧的最大变形进行测量,第一组平面板两侧的最大变形量分别为23.01 mm、23.41 mm,平均值为23.21 mm,第二组平面板两侧的最大变形量分别为25.18 mm、27.60 mm,平均值为26.39 mm,两组试验误差为12.05%。由两组试验后平面板的变形模式和变形量可以看出,两组试验结果较为相似,数据较为稳定,具有一定的可靠性。

图5 爆炸实验及数值模拟示意

图5(c)为数值模拟获得的变形云图,(以X向为迎爆面),U1表示X方向的位移。与图5(b)对比可以看出,二者变形基本一致,四角有明显的塑性变形,最大位移在抗爆框架两侧中心处,对称分布;模拟得到的两侧最大变形量均为24.82 mm,与两组实验平均值24.80 mm相比,误差仅为0.08%。由上述分析可见,新建立模型模拟结果与试验结果在变形模式上基本一致,最大变形量基本相同,Johnson-Cook本构模型和CONWEP控制方程可以较好地模拟钢结构在气云爆炸下的动态响应过程,基于该模型进行波纹板截面参数抗爆性能影响因素分析具有实际参考意义。

3 影响因素分析

在工程中,波纹板在爆炸冲击下的变形量是衡量其抵抗爆炸能力的重要指标,因此本文以变形量这一参数作为其抗爆性能影响程度的指标。先对波纹板在爆炸荷载下的动态响应过程进行分析,后分别对波纹板厚度t为1～5 mm、波宽L1为30～70 mm、坡宽L2为30～70 mm、坡深h为30～70 mm的模型进行模拟分析。

3.1 波纹板在爆炸荷载下的动态响应过程

为探究波纹板在爆炸荷载下的动态响应过程,以厚度t为3 mm、波宽L1为50 mm、坡宽L2为50 mm、坡深h为50 mm的波纹板模拟结果为例进行分析,图6为该结构特征波纹板在2 kgTNT炸药下的最大塑性变形点的变形时程曲线。

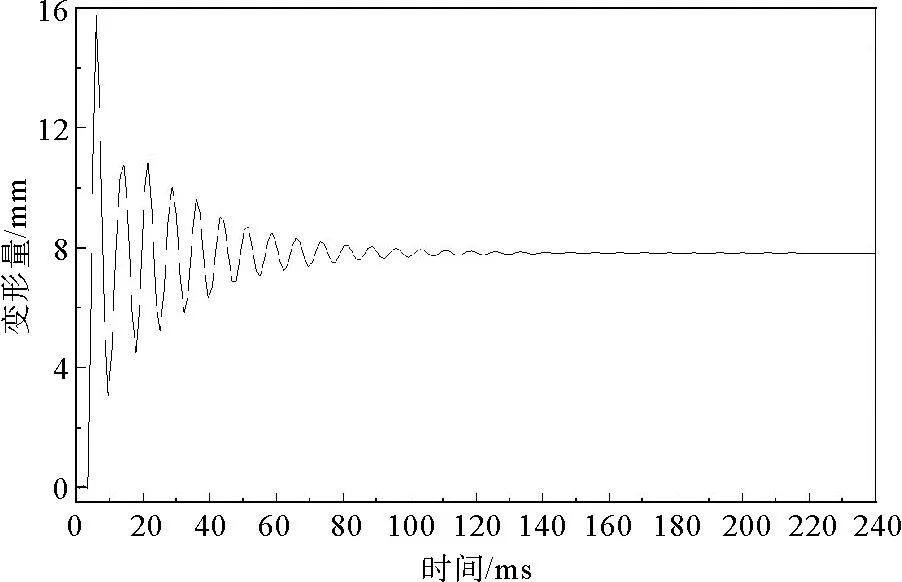
图6 波纹板变形时程曲线

从图6可以看出,波纹板动态响应过程可分为3个阶段——冲击波传播阶段、波纹板振动阶段、稳定阶段。冲击波传播阶段的持续时间主要取决于爆源至波纹板的距离,本试验炸药在0时爆炸,距离波纹板3 m,传播时间约为3 ms;当冲击波到达波纹板时,波纹板受到爆炸荷载冲击作用发生变形,进入振动阶段,该阶段从3 ms持续至约220 ms,约6 ms时变形量迅速达到峰值,最大变形约15.85 mm,而后波纹板开始进行有规律的振动,该阶段主要特征是以最终塑性变形量为轴进行振动,振幅不断减小;220 ms后进入稳定阶段,波纹板趋于稳定并处于最终塑性变形,变形量约为7.84 mm。

3.2 厚度t对抗爆性能的影响

取波纹板厚度t分别为1,2,3,4,5 mm,其他特征参数(波宽L1为50 mm、坡宽L2为50 mm、坡深h为50 mm)保持不变进行模拟,得到波纹板受爆炸冲击后的动态响应过程,取5种参数下波纹板最终塑性变形量最大点绘制其变形时程曲线,如图7所示。从图7中可以看出厚度对波纹板变形量影响较大,将不同厚度波纹板的最大变形量和最终塑性变形量列于表2,可以看出随厚度增大,波纹板变形量呈指数减小,这可能是由于板厚的增加提高了波纹板的抗弯强度,从而提高了其抵抗爆炸冲击的能力。此外,由图7可得,随着厚度的增加,波纹板在爆炸荷载下的振动频率有一定的提高,且厚度为4 mm和5 mm的波纹板在爆炸初期的变形量出现负值,说明其产生的塑性变形较小,基本处于弹性变形。

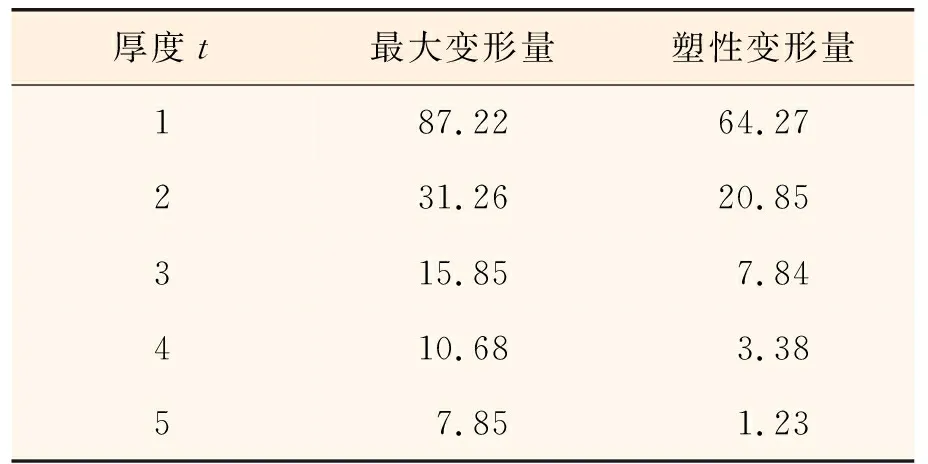
表2 不同厚度t下波纹板最大变形量和塑性变形量 mm

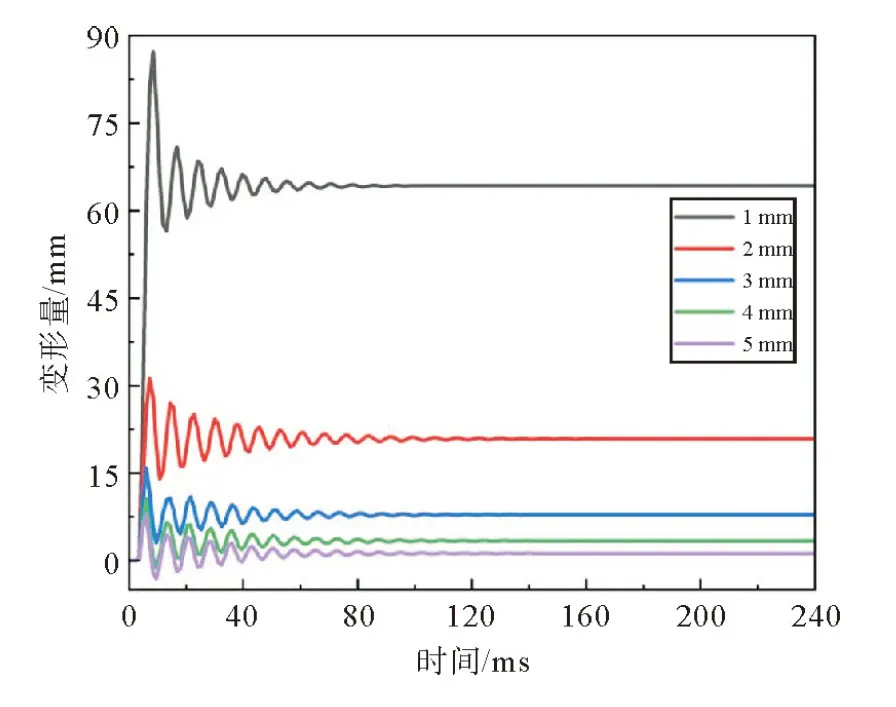
图7 不同厚度t下波纹板变形时程曲线

3.3 波宽L1对抗爆性能的影响

取波纹板波宽L1分别为30,40,50,60,70 mm,其他特征参数(厚度t为3 mm、坡宽L2为50 mm、坡深h为50 mm)保持不变进行模拟,得到波纹板受爆炸冲击后的动态响应过程,取5种参数下波纹板最终塑性变形量最大点绘制其变形时程曲线,如图8所示,将不同坡宽L1下波纹板最大变形量和塑性变量列于表3。从图表中可以看出波宽的变化对波纹板的最大变形影响较小,5种波宽下的最大变形相差仅为7.4%,但其对波纹板塑性变形影响较大,塑性变形量与波宽呈正相关;在波纹板振动方面,波宽对其振幅和振动频率均有一定的影响,在振幅方面影响较为显著。

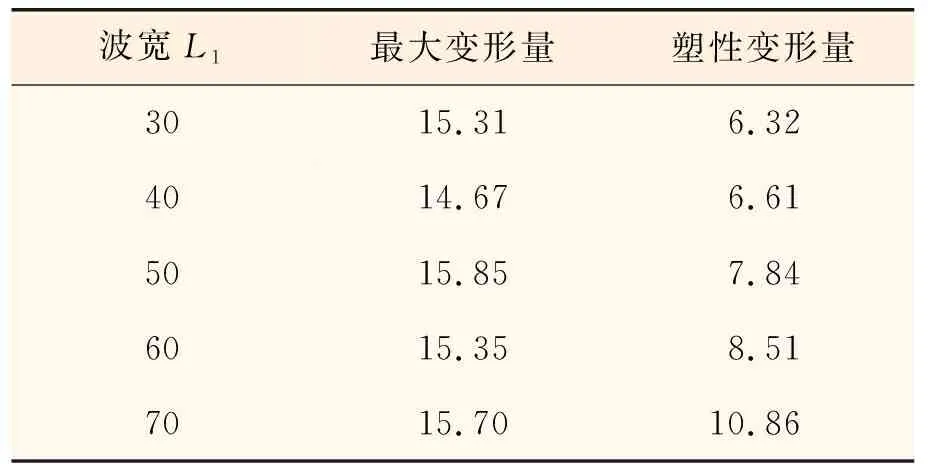
表3 不同波宽L1下波纹板最大变形量和塑性变形量 mm

图8 不同波宽L1下波纹板变形时程曲线

3.4 坡宽L2对抗爆性能的影响

取波纹板坡宽L2分别为30,40,50,60,70 mm,其他特征参数(厚度t为3 mm、波宽L1为50 mm、坡深h为50 mm)保持不变进行模拟,得到波纹板受爆炸冲击后的动态响应过程,取5种参数下波纹板最终塑性变形量最大点绘制其变形时程曲线,如图9所示,将不同波宽L2下波纹板最大变形量和塑性变形量列于表4。由图表可得,坡宽对波纹板的最大变形和塑性变形有一定的影响,二者呈正相关性;在振动方面,对波纹板的振动频率有轻微影响,对振幅有较为显著的影响。

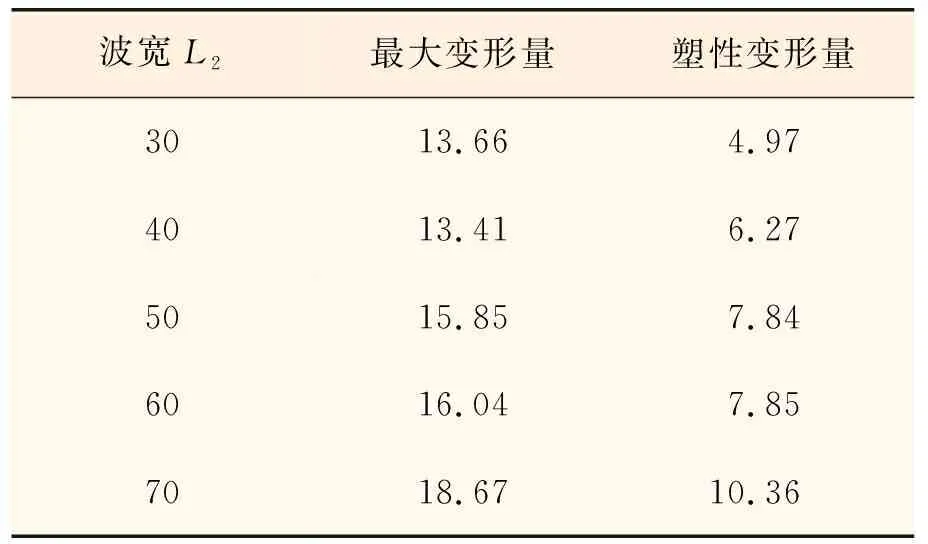
表4 不同坡宽L2下波纹板最大变形量和塑性变形量 mm

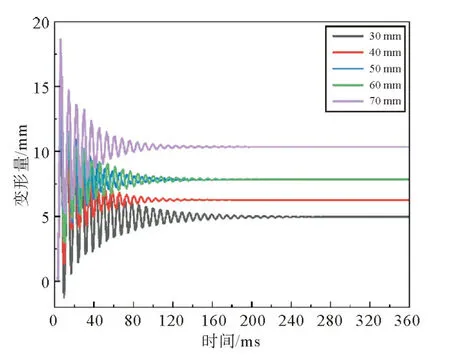
图9 不同坡宽L2下波纹板变形时程曲线

3.5 坡深h对抗爆性能的影响

取波纹板坡深h分别为30,40,50,60,70 mm,其他特征参数(厚度t为3 mm、波宽L1为50 mm、波宽L2为50 mm)保持不变进行模拟,得到波纹板受爆炸冲击后的动态响应过程,取5种参数下波纹板最终塑性变形量最大点绘制其变形时程曲线,如图10所示,将不同坡深h下波纹板最大变形量和塑性变形量列于表5。由图表可知,坡深对波纹板的影响显著,随坡深增加,波纹板最大变形量和最终塑性变形量呈指数减小,这可能是由于坡深的增加使波纹板的坡面面积及转角增大,增强了其抗弯强度,从而提高了抗爆能力;坡深在波纹板振动方面影响也十分显著,随着坡深增加,其振幅不断减小,振动频率加快,波纹板振动阶段持续时间明显缩短,更快地趋于稳定。

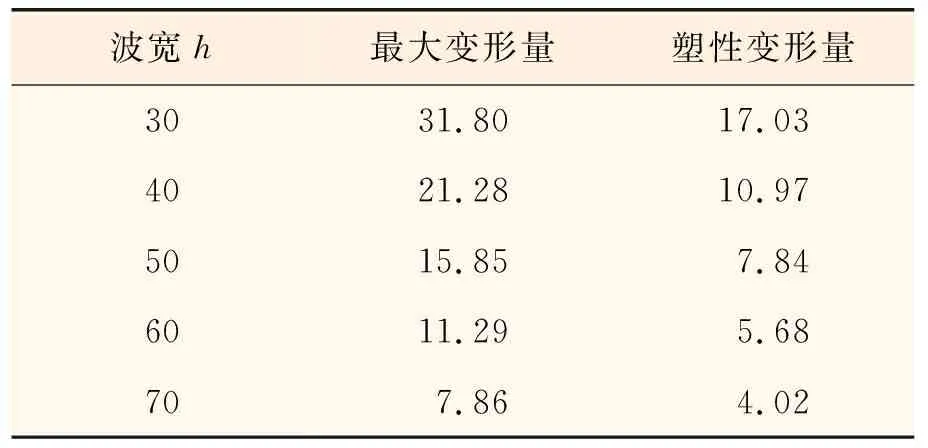
表5 不同坡深h下波纹板最大变形量和塑性变形量 mm

图10 不同坡深h下波纹板变形时程曲线

3.6 截面参数对抗爆性能影响方差分析

为进一步探究波纹板截面参数对其最大变形、最大塑性变形的影响,本文设计了4因素4水平的正交试验进行分析,因变量分别为最大变形量、最大塑性变形量,试验设计如表6所示。

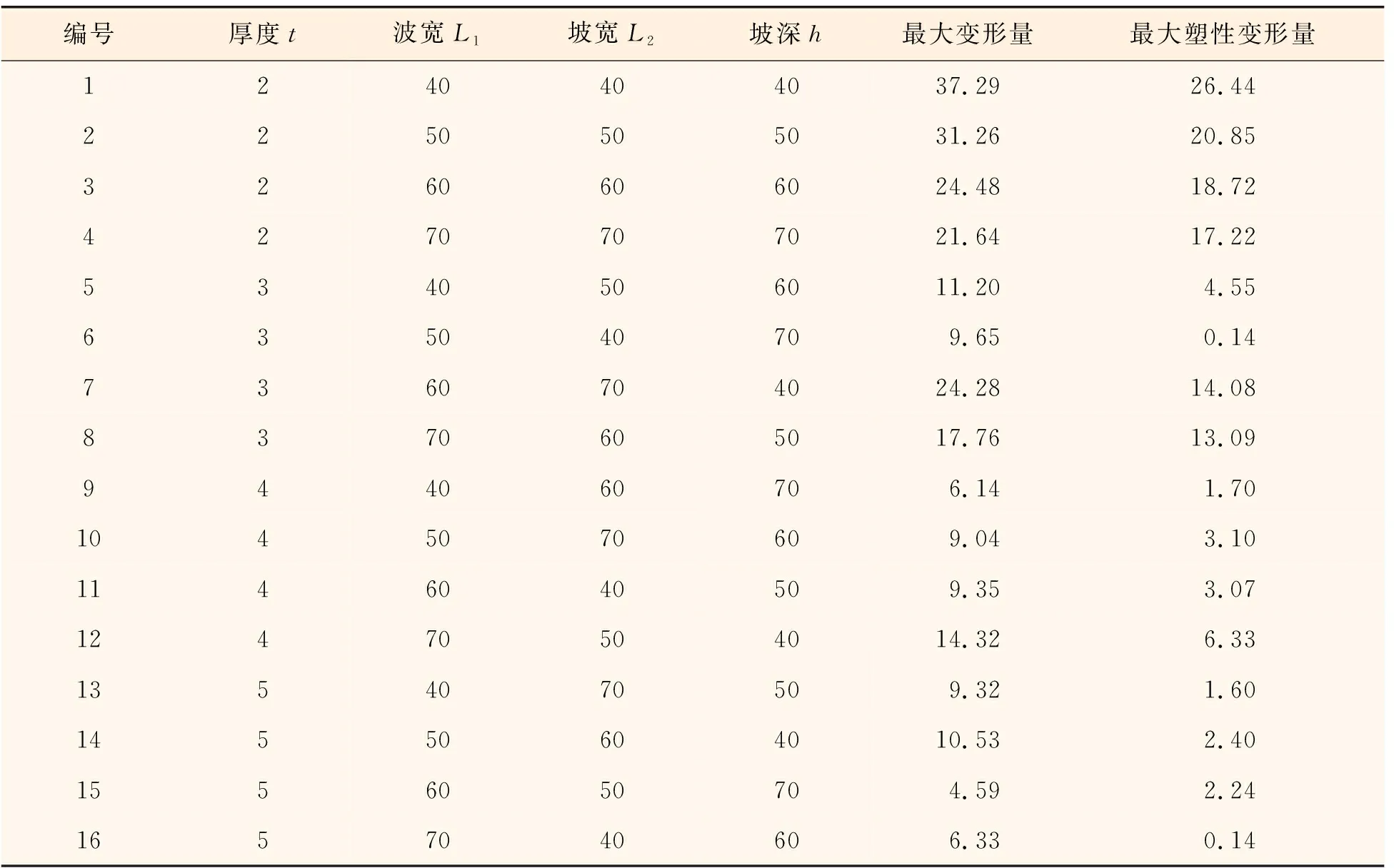
表6 截面参数正交试验设计 mm

表7、表8分别为最大变形量、最大塑性变形量正交试验的方差分析结果。其中,表格显著水平的**表示影响非常显著;*表示影响显著,-表示影响不显著,从表中可以看出,在波纹板最大变形方面,截面特征参数中的厚度t对波纹板最大变形的影响最为显著,其次坡深h也有较为显著的影响,波宽和坡宽影响较小;而在最大塑性变形方面,仅波纹板厚度对其影响较大,坡深、坡宽及波宽对其影响较弱。故在进行波纹板设计时,在满足成本要求的前提下,可尽量增加波纹板的厚度和坡深,以提高其抗爆性能,此外,根据3.3、3.4所述,还应尽量降低波宽、坡宽以降低其振幅和最终塑性变形。

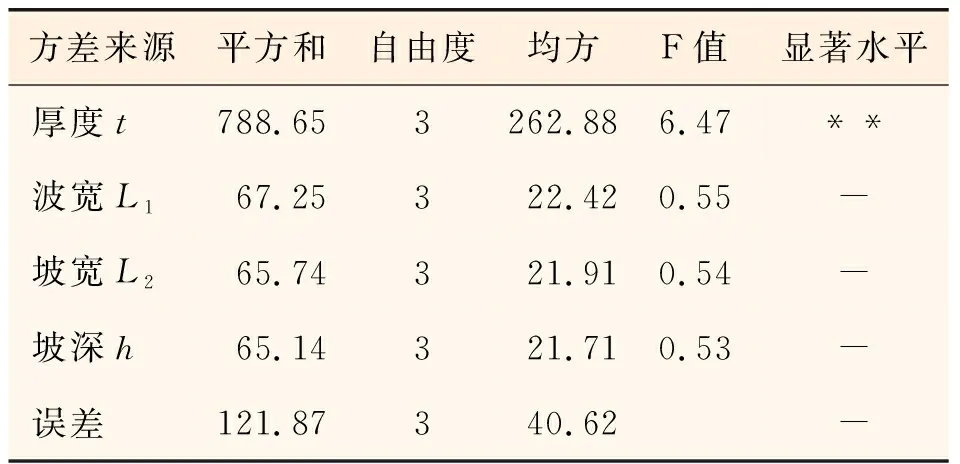
表8 正交试验最大塑性变形量方差分析

4 结论

本文通过数值模拟和实验验证,对气云爆炸冲击状态的波纹板动态响应过程及影响因素进行了分析,得到以下结论:

a) 通过爆轰实验验证,Johnson-Cook本构模型可以较好地模拟出Q235B钢在大变形、高应变率情况下的变化,CONWEP控制方程可以较好地模拟气云爆炸,二者结合模拟波纹板在气云爆炸下的动态响应特性具有实际参考意义。

b) 分析了波纹板在冲击下的动态响应过程,其可以分为3个阶段——冲击波传播阶段、波纹板振动阶段、稳定阶段,振动阶段以最终塑性变形量为轴振动,且振幅逐渐减小,直至波纹板稳定至塑性变形处。

c) 通过控制变量法得出波纹板厚度t、波宽L1、坡宽L2、坡深h4个参数对波纹板的影响规律,即厚度、坡深与变形量呈负相关,波宽、坡宽与其呈正相关;而后设计正交试验,借助方差分析方法,得出厚度t对波纹板变形影响最为显著,其最大变形量和最大塑性变形量F值分别为23.22、6.47;坡深h次之,最大变形量和最大塑性变形量F值分别为6.22、0.53;波宽L1、坡宽L2影响较小,最大变形量和最大塑性变形量F值分别不超过0.1、1。因此可通过调整截面参数优化波纹板抗爆性能,为波纹板的设计提供参考和指导。