杨森公式和深仓侧压力计算
2024-04-16张美梅李新南
张美梅,李新南
(上海市建筑材料工业设计研究院有限公司,上海 200032)
0 引言
圆筒仓(深仓)广泛应用于建材和粮食等行业的物料贮存。目前,对于深仓侧压力的计算,国内外普遍采用杨森计算公式。在GB 50077—2003 《钢筋混凝土筒仓设计规范》中也明确规定,深仓侧压力计算以杨森公式为主,并辅乘修正系数来进行调整。这种计算方法已延续多年,但我们在引用计算公式时发现,杨森公式无论在计算假设还是在计算所得结果方面均存在很多问题。因此,必须深入研究这些问题产生的根源并予以解决。笔者依据散粒体的物理特性,在研究和分析杨森公式的基础上,推导出新的深仓侧压力的计算公式。
1 杨森公式的运用及问题分析
当前计算圆形深仓中的散粒体对仓壁和仓底所产生的压力时,杨森公式的推导依据如下。
假设散粒体任意一点(包括仓壁)的水平压力qx与垂直压力qz成正比。即:
式中:Ka为主动侧压力系数。
假设散粒体沿仓壁滑动的阻力为τ:
式中:f0= tanφ0为散粒体与仓壁的摩擦因数;φ0为散粒体与仓壁的摩擦角。
在距仓顶深度为Z处取一层厚度为dz的贮料单元体,如图1 所示。单元体上的作用力有:自重γFdz(F为单元体面积,γ为散粒体重度),垂直压力qz和下面的反力qz+ dqz,仓壁上的滑动阻力τ。列出在各力作用下的平衡方程,对该方程进行积分,最后得到杨森公式中垂直压力qz的计算式:

图1 贮料单元体受力示意Fig.1 Schematic diagram of the force of the storage unit
仓壁的水平压力qx可利用式(1)求解。虽然杨森公式已成功应用于深仓的设计实践,但是早期依据杨森公式设计的钢筋混凝土深仓屡次出现问题,主要表现在仓壁出现垂直裂缝。许多学者为追查原因而进行多次试验,发现式(3)给出的计算压力与实际压力相比偏小,因而许多国家的筒仓计算规程和我国的筒仓计算规范规定:仓底长度为2/3仓高的下部仓壁的水平压力qx比式(3)计算出的水平压力增大一倍。由此可见,杨森公式是一个被试验所推翻的计算公式,可以说杨森公式的假设是不成立的。
前苏联学者克列因认为:试验结果与杨森公式的差别主要是按式(1)给出的主动侧压力系数Ka偏低。因为刚性仓壁的弹性位移太小,散粒体不可能出现完整的滑动面,不可能产生主动侧压力。所以克列因主张在计算时采用静止侧压力系数K0,它比极限状态下的Ka值大很多,例如谷物的平均Ka= 0.3,而K0= 0.7。
依据克列因的分析,分别采用Ka= 0.3 和K0=0.7代入式(1)和式(3)进行计算,所得结果是:2种情况下的仓底水平压力几乎一致,但仓底的垂直压力却有差距,与实际压力相比,式(3)所得结果还是偏小很多,由此可见,杨森公式计算所得结果比实际压力偏小的原因不是主动侧压力系数Ka偏低,而在于假设基本不成立。
对式(3)进行研究和分析后得到:式(3)给出的计算压力比实际压力偏小的原因在于杨森公式的第二条假设:考虑散粒体沿仓壁滑动的阻力τ,这个阻力τ的计算值很大,致使仓底的垂直压力减小很多。由于qz减小,仓底的水平压力qx也随之减小。现通过计算例题进行说明。
设有一组深仓,高h=20 m;内径D分别为5、8、10、12 m;γ=17 kN/m³;散粒体的内摩擦角φ= 30°,散粒体与仓壁的摩擦角φ0= 25°。
按式(3)和式(1)计算出每种仓的仓底垂直压力qz和仓底水平压力qx。每种仓散粒体总重W,每种仓仓壁总的摩擦阻力∑τ,∑τ和W的比值,计算结果见表1。

表1 各种内径筒仓qz、qx、W、∑τ和β的计算结果Tab.1 Calculation results of qz、qx、W、∑τ and β of various inner diameter silos
(1)当不考虑阻力τ时,深仓仓底的垂直压力应为:qz=γh= 17 kN/m3× 20 m = 340 kPa。考虑阻力τ后,仓底的qz减小很多。如D=5 m 的深仓,qz由340 kPa 减小至126 kPa,β=0.63。即使是D=12 m 的深仓,qz也由340 kPa 减小至211 kPa,仓中散粒体的重力很多都转至仓壁上,致使仓底的qz和qx均比实际压力小很多。
(2)计算深仓时,是否应考虑τ值?按照杨森公式的假设,散粒体沿仓壁滑动而产生阻力τ。但是当贮料静止时,散粒体不产生滑动,因而阻力τ也不存在。考虑了阻力τ以后,将使计算偏于不安全,计算所得的垂直压力qz和水平压力qx大幅度减小。结构计算的基本原则是考虑最不利的因素,而考虑阻力τ是有利因素。
2 “新的”深仓侧压力的计算
基本假设如下:1)依据散粒体的物理特性,深仓中散粒体对仓壁的作用力为E,其方向是由散粒体的内摩擦角φ指向仓壁;2)由于深仓仓壁的刚度很大,在计算时采用静止侧压力系数K0;3)仓中散粒体除了对仓壁产生水平压力qx外,还对仓壁产生垂直压力qy。
在深仓截面中,采用单位圆周长所对应的扇形截面abo作为计算单元,如图2所示。

图2 圆库贮料受力示意Fig.2 Schematic diagram of the force of the circular warehouse storage
图2 中,E为散粒体对仓壁所产生的作用力,力的作用方向是由散粒体的内摩擦角φ指向仓壁;Gz为距仓顶深度Z处扇形截面abo中的散粒体重量;qx为散粒体对仓壁所产生的水平压力,即静止侧压力;qy为散粒体合力E对仓壁所产生的垂直压力。
式中:Kw0为单位重量散粒体的静止侧压力系数。
目前引用的都是单位重量散粒体的静止侧压力系数K0,依据静止侧压力系数的定义:静止侧压力系数为水平应力σh和垂直应力σv的比值,即:
但是目前所引用的静止侧压力系数K0却不符合定义。目前计算静止侧压力的公式为:
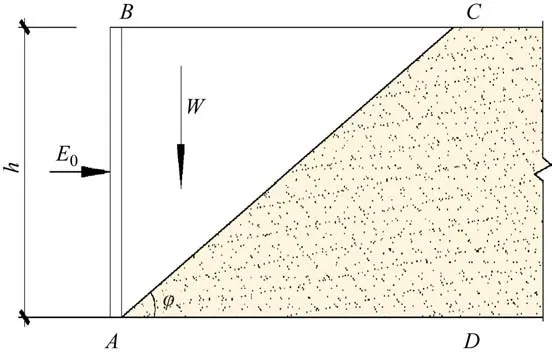
图3 散粒体作用于挡墙示意图Fig.3 Schematic diagram of the action of the bulk particles on the retaining wall
由式(9)和式(10)得:
在距仓顶深度为Z处扇形面积上散粒体的重量为:
式中:R为深仓半径。
重量为Gz的散粒体对仓壁所产生的静止侧压力即水平压力为:
因为计算所取的单元为扇形,而扇形面积仅为矩形面积的一半,所以在求水平压力qx时,必须乘上面积折减系数S=0.5,此时式(13)改为:
依据散粒体的物理特性,散粒体对仓壁作用力E的方向是由散粒体的内摩擦角φ指向仓壁,因此散粒体除了对仓壁产生水平压力qx外,还对仓壁产生垂直压力qy:
单元体中散粒体的重量原是Gz,由于产生垂直压力qy,因而Gz减小为:
由于散粒体的重量由Gz减小为G,因而散粒体对仓壁所产生的水平压力qx为:
代入式(15),整理后得到仓底垂直压力的计算式为:
由式(19)可知,仓底垂直压力仅与仓高H和φ有关,而与仓径大小无关。
计算例题:深仓内径D=10 m,高h=20 m,γ=17 kN/m³,φ=30°,静止侧压力系数K0= 1 - sinφ=0.5,要求计算仓底水平压力和仓底垂直压力。
仓底单元扇形面积上散粒体重量GH为:
单元散粒体对仓壁所产生的垂直压力qy为:
3 算例及分析
为了研究和分析深仓中散粒体产生的水平压力和仓底垂直压力,对一组深仓进行计算。
设有一组钢筋砼深仓:仓高h均为20 m;仓直径D分别为5、8、10、12 m;贮料的散粒体内摩擦角φ为40°、35°、30°和25°;散粒体重度γ=17 kN/m³,散粒体与仓壁的摩擦因数f0=0.466;静止侧压力系数K0=1 - sinφ。计算仓底垂直压力和水平压力。
按以下3 种计算方法进行计算:1) 杨森公式。2) “筒仓计算规范”所规定的方法。3) 本文所推导的公式。结果详见表2。依据表2中计算结果可知:

表2 用3种公式计算所得各直径深仓不同贮料的水平、垂直压力Tab.2 Horizontal and vertical pressure results of different storage materials of each diameter deep silo calculated from 3 formulas
(1) 杨森公式计算所得结果的确偏小很多。
(2) 杨森公式假设散粒体对仓壁的作用力是垂直于仓壁的,这不符合散粒体的物理特性。依据散粒体的物理特性:散粒体对仓壁的作用力方向是由散粒体的内摩擦角φ指向仓壁。
(3) 杨森公式引用主动侧压力系数Ka来计算散粒体的侧压力。由于仓壁不存在位移,实际上这个系数在计算中是不存在的。
(4) “筒仓设计规范”对深仓侧压力的计算规定以杨森公式计算为依据,考虑到杨森公式计算结果比实际压力偏小太多,因而在使用杨森公式计算时,引用贮料压力的修正系数C,使杨森公式计算所得结果比较符合实际压力。“规范”规定,仓底垂直压力的修正系数Cv=1.4;在长度为2/3 仓高的下部仓壁,仓底水平压力的修正系数Ch=2.0。按照杨森公式的假定:散粒体的任意一点的垂直压力qz与水平压力qx成比例,为什么在引入修正系数C进行调整时,水平压力qx的修正系数Ch=2.0,而垂直压力qz的修正系数Cv=1.4?这是由于引用了偏小的修正系数,使得垂直压力的计算结果偏小很多。
本文所推导的计算公式主要依据是引用了散粒体的静止侧压力,因而静止侧压力系数K0的取值是否恰当,将影响到压力的计算值是否符合真实的压力值。在表2 中,计算所采用的K0值是引用Jaky 所提出的K0= 1 - sinφ的经验计算公式。该式是在大量室内试验的基础上经统计而得到的。由于是经验公式,不可能把全部试验数据都归纳进去,因而误差难以避免。由于K0值的不定性,导致本文计算公式所得结果与实际压力可能存在偏差。
按“规范”规定:杨森公式计算结果乘以修正系数后所得的压力值存在3 种情况:1) 与实际压力相符合;2) 比实际压力偏大;3) 比实际压力偏小。
4 结语
本文推导得出的公式主要依据散粒体的物理特性,以及假设圆筒仓中散粒体所产生的侧压力是静止侧压力。公式的物理概念清楚且计算简单。由实例计算结果得知,本文公式计算所得结果与“规范”所规定的计算方法所得结果比较接近,有些甚至是相同的。
