基于混合启发式算法的中小学布局优化研究
2024-04-16王旭杰
王旭杰,杨 莉
(1.湖北师范大学 计算机与信息工程学院,湖北 黄石 435002;2.湖北第二师范学院 计算机学院,武汉 430205)
1 引言
新中国成立初期,为普及义务教育,保障适龄儿童的受教育权,国家基本采取适龄儿童就近入学的原则。就近入学政策不断发展与完善,如今已实现中小学生就近入学,满足了群众“有学上”的愿望和需求。随着社会经济的快速发展与人民生活水平的不断提高,人们对于教育的追求已经从“有学上”向“上什么样的学校”转变。放弃就近入学而寻求更优质教育资源的行为越来越多,为争取优质教育资源而展开的择校竞争愈演愈烈。中小学校分布不均衡、学区划分不合理的现象以及家长们对于“重点学校”的趋之若鹜,引发了一系列关于学生上学距离增加、学校容纳规模不足、优质教育资源不足以及校际教育资源分配不均衡的问题。如何优化学校布局,满足地区适龄儿童上学需求、改善优质教育资源分配不均等问题被越来越多的学者所关注。
近年来,专家和学者对学校布局优化模型提出了改进思考。2011年,孔云峰和吕建平从空间角度出发,考察了择校问题。他们基于学校与居民点之间的空间关系,引入了最近距离模型、引入模型和Huff模型,并在ArcGIS软件中进行了模型的分析。研究结果显示,Huff模型的性能较为优越。[1]随后,孔云峰以就近入学为目标,依据学校、居民点和道路网络构建了最优学区划分的整型规划模型。在GIS软件的支持下,开发了最优学区划分工具。[2]杜梓宁运用ArcGIS网络分析研究中小学的服务区,针对中小学存在的分布不均、数量不足、服务区重叠等问题提出解决方案。[3]徐铎轩以东北地区城乡发展不均、乡镇中小学基础教育资源不足为切入点,通过综合调研和量化研究,为校园选址优化和空间布局设计两方面提出策略。[4]何雪针对单校划片和多校划片的复杂性,通过混合启发式算法,包括M-ILS-SA、M-ITS-SA和M-VND-SPP,结合空间同位模式挖掘和道路网络图计算学生入学距离,提出了有效解决学区划分问题的方法,确保空间连续性、具备良好寻优能力和收敛性,并在多次启动下实现全局优化和快速收敛。[5]陈玉龙通过改进的模拟退火算法改善交通网络条件有效提高了学生的上学效率。[6]陈春萍采用GIS技术和网络分析法,通过加权叠加分析与量化因子选取,优化了现有学校资源的空间布局。[7]周萌基于密度估计分析供需关系,优化小学布局,生成基于供需平衡的学区划分图,最终提出义务教育学区划分优化建议。[8]
本文运用TS-SA混合启发式算法构建教育资源空间优化框架,如图1所示。第一,根据《湖北省义务教育学校办学基本标准》规定小学与初中在校生人数均不得超过2000人。考虑学生就近入学可达性与学校最大容量设计优化算法,重新分配学生对口学校。第二,针对处于教育服务盲区的学生分布特征,采用ArcGIS核密度分析法确定最优新建学校个数,并将聚集点的中心作为初始建校地址,以实现就近入学和服务覆盖最大化为目标。通过TS-SA算法对新建中小学选址位置进行调优。
2 算法理论介绍
2.1 Haversine距离计算
Haversine距离计算方法是一种广泛应用于地理信息系统和位置服务的球面距离估算技术。相较于欧式距离在平面上的计算,Haversine距离考虑到了地球表面的曲率,更加准确地测量了两个地理坐标点之间的实际表面距离。假设两点的经纬度分别为(lon1,lat1)和(lon2,lat2),其对应的弧度表示为和。
弧度计算表达式如公式(1)与公式(2)所示:
运用球面三角法将经纬度转换为弧度,式中lon与lat分别代表经度与纬度,π 为圆周率,180是度到弧度的转换系数。
Haversine所得实际距离的计算公式如下:
公式(3)与(4)中Δlat、Δlon分别表示两坐标之间的纬度差值与经度差值;式(5)中a代表计算的中间变量,利用三角函数运算考虑地球曲率对距离的影响。公式(6)中的c代表两点之间的弧度距离。公式(7)中的d为最终的Haversine距离,R是地球的平均半径,通常取6371公里。
2.2 ArcGIS核密度分析
核密度分析是一种用于估计空间上事件分布密度的地理信息系统分析方法。该方法通常用于确定地理空间中事件、点或特定现象的密集程度,以便揭示潜在的空间模式和趋势。
该分析方法是通过在每个时间点周围创建一个核(通常为高斯核)来估计每个位置的事件密度。核函数在每个事件的位置上形成一个权重,表示该位置的贡献。通过在所有事件位置上应用核函数,形成一组权重,这些权重用于平滑地估计整个研究区域内的事件密度。最终产生一个密度表面,显示了空间上每个位置的事件密度估计。
2.3 TS-SA算法
TS-SA是一种综合了禁忌搜索算法和模拟退火算法的混合启发式算法,旨在有效解决学生分配问题。该算法的基本思路如下:在初始解构建阶段,采用随机分配的方式将学生随机分配到学校。在TS算法的优化阶段,进一步优化已生成的初始解。这一过程涉及对已构建的初始解进行多轮优化,通过邻域搜索算子获取多个不同的优化解。然而,这些解并不一定是最优的,因此需要通过SA模型进一步优化。在SA模型的再优化过程中,以TS算法形成的解作为初始解,执行更优的解搜寻。这种综合算法的设计旨在充分利用两种启发式算法的优势,以提高问题解决的效率和质量。整体算法流程图如图2所示。

图2 TS-SA算法流程图
2.3.1 TS算法优化
TS算法以随机创建的初始解为基础,通过建立禁忌表,对优化的过程进行存储和记录,防止算法重复搜索。在每一次迭代的禁忌搜索中,都通过对当前解的随机微调产生新的邻域解。TS算的优化过程具体步骤如下所示:
第1步:初始化禁忌表TabuTable,将当前所得簇的中心作为初始解加入TabuTable中。
第2步:基于当前学校分配方案,以最小化区域内学生上学距离总和作为目标函数,当达到最大迭代次数或终止条件时停止搜索,终止条件如公式(8)和(9)所示。
小学终止条件:
初中终止条件:
式中Nstudent为区域内学生人数,S为区域内学生上学距离总和,根据《中小学校设计规范》中规定小学上学距离不超过500米,初中上学距离不超过1000米,当区域内学生上学距离总和小于或等于两者的积时停止局部搜索。
第3步:将随机产生的解为禁忌搜索算法的初始解,并通过对当前解的随机微调产生新的邻域解。
第4步:判断微调后的邻域解是否存在TabuTable 中,若存在,转至第3 步产生新的邻域解,若不存在则继续。
第5步:引入目标值评估函数,判断是否接受该禁忌搜索解,若接受,更新当前解,转至第1步;否则将不接受的解添加至TabuTable中,转至第2步。
第6步:循环直至到达终止条件或最大迭代次数。
2.3.2 SA算法再优化
SA算法采用具有概率跳突特征的Metropolis 抽样准则,以概率的方式接受邻域中较差的解,以增强算法的多样性,能够有效地避免陷入局部最优并实现全局最优。本文以当前区域内学生上学总距离作为初始温度,以区域内学生人数作为终止温度,构建SA模型对学校分配方案进行再优化。SA算法再优化的具体步骤如下所示。
第1步:设置外部循环迭代指标,最大迭代次数。
第2步:根据当前学校分配方案计算区域内学生上学总距离,若小于则结束运算,则通过随机微调当前学校经纬度地址产生新的领域解,以表示邻域解状态。
第3步:计算目标增量;设,若>0或当<0且时,接受该邻域解,更新当前学校分配方案,否则不接收邻域解,转至第2步。
第4步:循环直至到达终止条件或最大迭代次数,求解出最终方案。
3 数据来源及预处理
3.1 数据来源
本文研究数据主要包括学生的“家-校”位置信息、2021武汉市行政区划、基于《2021武汉统计年鉴》获得中小学教师信息、武汉市常住人口数据以及基于百度地图开放平台获得的学生上学实际距离等基本信息。具体数据说明如表1所示。

表1 研究数据说明
3.2 数据处理
3.2.1 家-校原始信息处理
本研究所使用数据集原始数据组成如表2所示中包含学生户籍地址、学生现住址以及学生所在学校三个纬度。

表2 原始数据集示例
对于原始数据中所存在的将现住址填写为户籍地址的情况,如表3 所示。为了不在“家-校”距离计算时产生离群数据,从而影响后续的就近入学现状评估与空间优化,本研究选择删除现住址不在研究区域内的数据。

表3 离群数据示例
3.2.2 家-校经纬度地址转换
为了得到学生上学的真实距离与时间和后续模型构建时转换为可输入的数据,需要将具体的家庭住址与学校住址转换为经纬度地址。本研究运用百度地图开放平台中的批量地理编码功能进行转换,转换结果如表4所示。
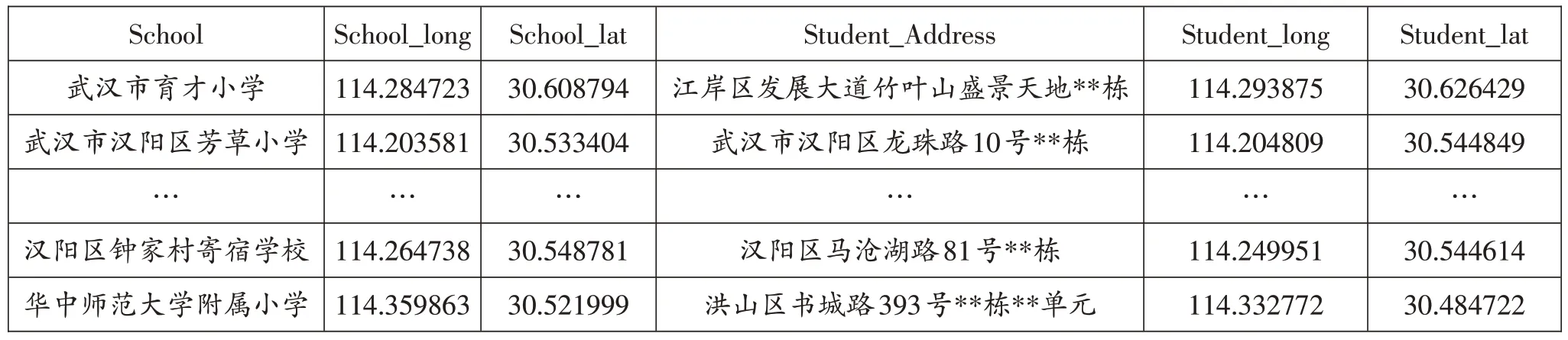
表4 百度地图获取的经纬度信息
百度地图开放平台所使用的坐标系为百度坐标系(bd09II),本研究所使用的区域行政边界矢量图为WGS84 地理坐标系,两者之间存在一定的经纬度偏差,所以需要统一坐标系,将百度坐标系地址转换为WGS84坐标系。转换结果如表5所示。

表5 WGS84坐标系转换结果
3.2.3 家-校距离计算
在先前的公共服务设施可达性测度中,通常采用欧式距离和网络分析中的路网距离等计算方法。然而,这些方法未考虑交通干道、河流等实际交通环境因素,导致距离度量结果与实际环境存在较大误差。随着基于位置服务技术的不断发展,互联网地图交通数据在可达性分析的距离测度中得到广泛应用。
为了真实评估中小学生的上学距离和上学时间,本部分利用百度地图开发平台获取实际交通状况下的旅行时间和距离。百度地图(http://map.baidu.com)具备实时更新和精准的空间数据,提供多种出行方式的最优路径规划,并能根据实时路况(例如道路阻断、交通管制等)计算准确的耗时。用户可以通过调用API 实现正/逆地理编码、路线规划、地点检索等功能。在本节中,使用Python 构建爬虫程序,调用百度地图Web 服务API,经过坐标转换和批量算路服务。部分输出结果如表6所示。

表6 百度地图获取的实际时间与距离示例
4 实验结果分析
4.1 评价指标
4.1.1 中小学可达性
本文采用基于百度地图获取的学生到学校实际步行时间评价中小学可达性。研究综合考虑了学生步行行为与实际交通环境的影响,旨在直观反映学生就学便捷程度。根据《城市居住区规划设计标准》GB50180-2018的规定,针对小学和初中教育设施,应在10分钟和15分钟的生活圈内进行配备。具体而言,小学的最佳步行可达时间不应超过10分钟,而初中的最佳可达时间应在15分钟以内。
4.1.2 中小学服务范围
在确定中小学服务半径阈值时,本研究依循《城市居住区规划设计标准》GB50180-2018的规定。根据该标准,小学的服务半径不应超过500米,初中的服务半径则不宜超过1000米。本研究将这一标准作为小学和初中规范服务区范围的依据。在度量学校服务范围距离时,采用了上一部分基于交通大数据的可达性分析,具体确定了实际步行距离500米和1000米范围,分别作为小学和初中的服务覆盖区。
采用服务覆盖率评价中小学教育服务能力。本文将中小学服务半径内所覆盖的人口占研究单元总人口的比例作为服务覆盖率指标,以此了解中小学教育服务覆盖的效率及评价单元之间的服务水平的差异。服务覆盖率越大,表明教育设施空间布局越均衡,服务面积越广,受益人口越多。计算公式如下:
式中,C表示服务覆盖率,∑PA表示区域内所有学校规范服务半径内所覆盖的总人口;A表示研究区域总人口。
本研究将学龄人口服务率作为中小学服务覆盖率指标,即中小学规范服务半径内(小学500米,初中1000米)覆盖的儿童或青少年人口占研究单元儿童或青少年总人口的比例。
4.2 研究结果
4.2.1 小学对口学校优化与建校选址
表7 展示了各行政区的平均在校生人数。通过观察发现汉阳区平均在校生人数最多,本节以汉阳区为例,展现小学对口学校优化与建校选址过程。

表7 各行政区在校平均人数
经过对口学校优化调整后,小学服务能力与可达性变动情况如表8所示,优化后小学500米学校服务率由18.20%提升至38.51%,被覆盖学生占比提高。最远上学距离保持不变,平均上学距离由3.01 千米缩短至2.85千米。另外,优化后仍有24.33%的学生上学距离超过2.5千米,说明相当一部分学生存在通勤困难。

表8 优化前后服务率与可达性比较
图3为经过优化后上学距离仍然超过了2.5千米学生的核密度分析图,通过观察学生聚集特征可知,在汉阳区的中部以及东南部存在大量上学通勤困难学生,需通过新建小学来解决这一问题。

图3 优化后服务盲区分布图
图4为新建学校的选址示意图,通过ArcGIS分析,拟新建了7所小学,再经过TS-SA混合启发式算法优化了学校选址。新建学校位于教育服务盲区的中心,较好地考虑了附近的学龄人口。

图4 新建学校选址
表9为新建学校前后的服务率与可达性变化情况。通过观察表格发现,新建学校后区域500米范围内的学校服务率由38.51%提升到了43.40%。上学超过2.5千米的人数减少了3.37%。平均上学距离由2.85千米下降到了1.779千米,上学距离标准差也有所下降,说明区域内学生上学距离之间差异性变小。最远上学距离缩短了3.234千米。整体服务率与可达性都相较于之前有了较大的提升。

表9 新建学校前后服务率与可达性比较
4.2.2 初中对口学校优化与建校选址
表10展示了各行政区的平均在校生人数。通过观察发现汉阳区平均在校生人数最多,但为与上一届中汉阳区小学的优化与新建保持差异性,本节选取在校平均人数仅次于汉阳区的江岸区为例,介绍初中对口学校优化与建校过程。经过对口学校优化调整后,初中服务能力与可达性变动情况如表11所示。优化后初中1000米学校服务率由21.16%提升至31.13%,被覆盖学生占比提高。最远上学距离保持不变,平均上学距离由12.58千米缩短至8.42千米,上学距离标准差由13.48千米下降至7.65,说明学生上学距离差异性减小。另外,优化后仍有39.36%的学生上学距离超过3.5千米,说明相当一部分学生仍存在通勤困难。

表10 各行政区在校平均人数

表11 优化前后服务率与可达性比较
图5为经过优化后上学距离仍然超过了3.5千米学生的核密度分析图,通过观察学生聚集特征可知,在江岸区的中部以及西南部存在大量上学通勤困难学生,需通过新建初中来解决这一问题。

图5 优化后服务盲区分布图
图6为新建学校的选址示意图,通过ArcGIS分析,拟新建了10所初中,再经过TS-SA混合启发式算法优化了学校选址。新建学校位于教育服务盲区的中心,较好地考虑了附近的学龄人口。
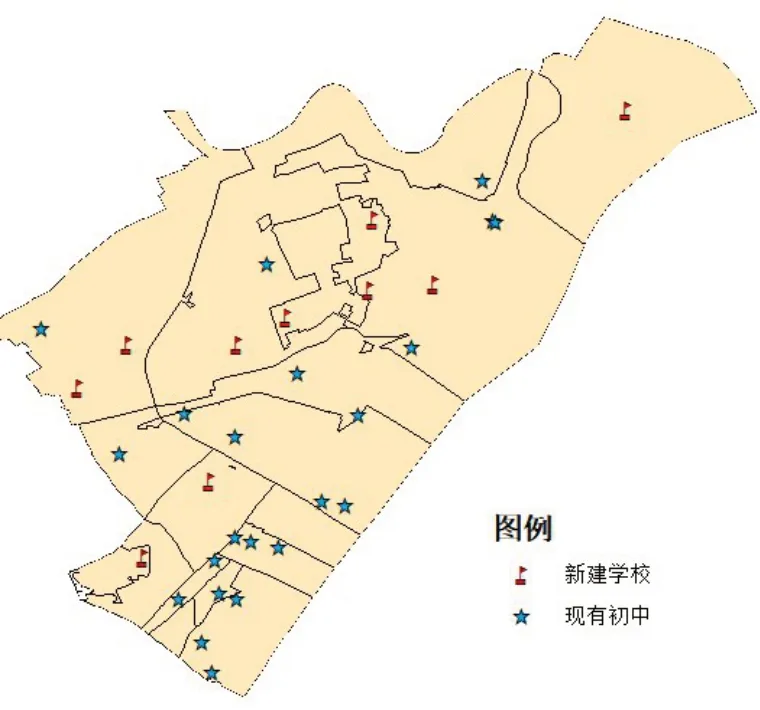
图6 新建学校选址
表12为新建学校前后的服务率与可达性变化情况。通过观察表格发现,新建学校后区域1000米范围内的学校服务率由31.13%提升到了52.68%。上学超过3.5千米的人数减少了10.63%。平均上学距离由8.42千米下降到了5.48千米,上学距离标准差也有所下降,说明区域内学生上学距离之间差异性变小。最远上学距离缩短了12.249千米。整体服务率与可达性都相较于之前有了较大的提升。
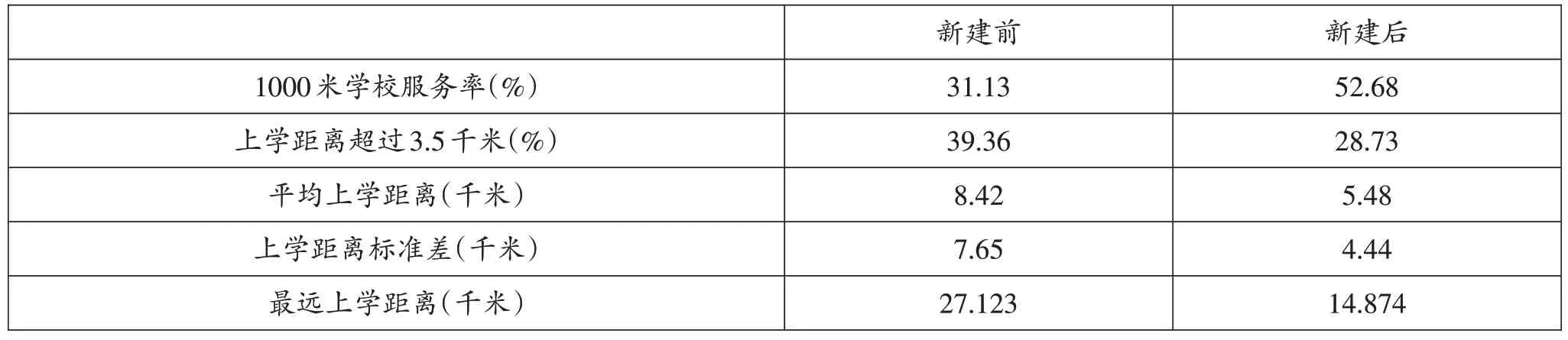
表12 新建学校前后服务率与可达性比较
5 结语
教育资源的空间分布和空间分配直接关系着居民享受教育服务机会的均等性与公平性。本文综合考虑就学人口分布、就学可达性、学校规模,以实现就近入学和均衡教育资源为目标,构建混合启发式算法TS-SA模型对现状中小学生对口学校进行调整。在此基础上,进一步筛选出教育服务盲区,通过ArcGIS分析教育盲区人口聚集特征,拟定新建学校数量,将聚集的中心点作为初始选址位置,再经过TS-SA算法对学校选址进行优化。通过模型对口学校优化,扩大了学校覆盖范围,缩减了学生上学距离。区域内学校服务率与学生就学可达性都有了明显的提升,较好地实现了教育均衡发展的优化目标。表明特征人口需求、学校就学可达性和学校承载力,在完善学生就近入学和提升教育服务均衡性方面具有积极作用。
