课程-迁移学习物理信息神经网络用于长时间非线性波传播模拟1)

郭 远 傅卓佳 , 闵 建 刘肖廷 赵海涛 ,3)

* (河海大学力学与材料学院工程与科学数值模拟软件中心,南京 211100)

† (中国三峡集团公司科学技术研究院,北京 101199)

** (河海大学土木与交通学院,南京 210098)

引言

非线性波传播广泛存在于众多自然现象和工程应用中,如水波[1-2]、光波[3]、声波[4]和地震波[5]等.非线性波传播的分析和模拟对于理解和控制这些现象具有重要的意义.然而,非线性波传播的数学模型通常是高度非线性的偏微分方程,它们的解析解很难推导得到或者不存在闭合的解析解[6],因此数值模拟是研究非线性波传播过程的主要方法之一.

目前,已有许多数值方法如有限差分法(finite difference method,FDM)[7]、有限元法(finite element method,FEM)[8]、谱方法(spectral method)[9]和格林函数方法(Green’s function method)[10]被成功用于求解波动方程,但是这些方法都存在一些局限性和挑战.例如,有限差分法和有限元法要求构造高质量的网格,谱方法和格林函数方法需要预先推导得到问题对应的谱函数及格林函数.此外这些方法在处理非线性问题时附加的非线性项也会影响其计算结果的精度和稳定性[11],特别是在解决长时间历程的非线性波传播问题时,这种影响尤为显著.

近年来,人工神经网络作为一种强大的机器学习工具[12-14],被广泛应用于各种复杂问题的求解和预测[15-18].特别是,物理信息神经网络(physicsinformed neural networks,PINN)将物理守恒定律和先验物理知识编码到神经网络中[19],通过最小化残差来求解偏微分方程.目前,PINN 已经被成功应用于求解各种非线性方程,如Schrodinger 方程[20-21]、Burgers 方程[22-23]、对流扩散方程[24-25]等.然而,PINN 也存在一些局限性和挑战;其中一个问题是PINN 难以进行长时间历程模拟[26-27].由于神经网络的参数空间是有限的,当时间域扩展到一定程度时,PINN 难以保持足够的精度和稳定性.此外,PINN 也可能受到初始条件、边界条件和噪声等因素的影响,导致训练过程陷入局部最小甚至发散[28].

为了克服这些问题,国内外研究者提出了一些解决方法.Meng 等[27]使用了一个串行的全求解域上的粗求解器和若干个并行的子域上的精细PINN,粗求解器的解用作每个子域中精细PINN 的初始条件,从而将一个长时间问题分解为许多独立的短时问题.Penwarden 等[29]提出了一种新的时域堆叠分解方法,通过遵循多种形式的因果关系并通过限制每次优化迭代所需的计算来提高可扩展性,并使用迁移学习方法来初始化域中的子网络和子域的基于容错的传播;上述两种方法的核心是将求解域分解并结合并行技术提高求解效率.Guo 等[28]结合重采样策略和现有的优化器组合技术并使用多重预训练策略来提高PINN 方法求解时间相关偏微分方程的收敛性和准确性,其本质上是一种课程学习技术.Xu 等[26]引入迁移学习来顺序更新深度算子网络(DeepONet),作为在不同时间帧中学习的传播子的代理,提高了DeepONet 长时间模拟的精度.

以上这些研究者的工作主要集中在时间一阶问题的研究上,并未涉及到本文研究的时间二阶波动问题.本文结合了Penwarden 等[29]时域堆叠分解的思想和Xu 等[26]迁移学习的方法,在Guo 等[28]提出的方法的基础上进行了改进和发展,提出了一种基于课程学习(curriculum learning)[30]和迁移学习(transfer learning)[31]的物理信息神经网络,简称为课程-迁移学习物理信息神经网络(CTL-PINN),并将其用于长时间非线性波传播分析.CTL-PINN 继承了PINN 的优点,相较于传统数值方法,无需划分网格,避免了网格数值算法中的网格畸变问题;能够融合方程与各种观测数据,形成物理和数据双驱动模型,对于处理反问题具有显著优势;在一定程度上规避了维数灾难,无论是一维、三维还是更高维问题,其实现方式都相同.与传统PINN 相比,CTL-PINN可求解的时域更长,训练结果更为精确和稳定.

1 基于课程学习和迁移学习的PINN 方法

1.1 瞬态非线性波传播问题

本文考虑如下瞬态非线性波传播问题,其控制方程可以表示为

其中,X为空间位置,Ω 为空间域,t为时间,T为求解的最后时刻,∇2为拉普拉斯算子,c为波的传播速度,u=u(X,t) 为待求位移,Q(X,t) 为已知波源函数,f(u) 为非线性项,其初始条件为

其中,ϕ (X) 和 φ (X) 是给定的函数,表示初始时刻的位移和速度分布,其边界条件为

其中,Γ1∪Γ2=Γ,Γ1∩Γ2=∅,Γ=∂Ω 为 Ω 的边界,Γ1为第一类边界条件或狄里克雷(Dirichlet)条件,Γ2为第二类边界条件或诺依曼(Neumann)条件,n是 Γ2上的单位外法向量,是给定的函数.

1.2 传统物理信息神经网络

PINN 方法通过深度神经网络(deep neural network,DNN)来近似方程(1)的解,其求解过程如图1 所示,神经网络的输入为时空坐标 (X,t),对应于方程(1)的时空自变量,输出是方程(1)的近似解uθ,其中 θ 为神经网络待优化参数.损失函数反映了方程的物理信息,它由3 部分组成:初始和边界条件的残差项以及控制方程的残差项,如下式所示

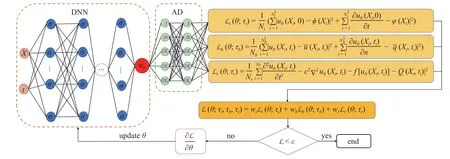
图1 传统PINN 求解瞬态非线性波动问题Fig.1 Solving transient nonlinear wave propagation problem by standard PINN

式(4)中,wi,wb和wr分别是损失函数中3 部分的权重,Li和 Lb分别表示初始条件和边界条件上的监督学习损失,Lr表示在残差数据集中定义的残差损失.式(5)～式(7)中,uθ(X,t) 为神经网络预测值,其各类导数可通过自动微分(automatic differentiation,AD)获得;根据速度和位移两类初始条件和两类边界条件,将Ni和Nb分为两部分,,Nb=Nr和 表示各训练点的个数,训练点通常通过随机采样获得.将初始条件和边界条件的数据集以及残差数据集分别保存为

通过最小化损失函数,神经网络输出的近似解uθ逼近真实解,PINN 可以在求解域内得到满足物理信息的预测.用 Σ 表示数据集的总和,即 Σ={τi,τb,τr},PINN 的训练就是一个使损失函数取得最小值的优化过程

神经网络优化算法常用的有Adam 算法和LBFGS 算法.神经网络参数 θ 的更新通过反向传播算法来实现,激活函数 σ 是高阶可微的,常用的有tanh和sin.

1.3 课程-迁移学习物理信息神经网络

本文引入课程学习和迁移学习技术,提出了课程-迁移学习物理信息神经网络(CTL-PINN),将其应用于长时间物理力学行为模拟.如图2 所示,CTLPINN 求解长时间历程问题可分为三个阶段:第一阶段是预训练,采用传统PINN 方法在短时间内进行;第二阶段是课程学习,用于时域扩大;第三阶段是迁移学习,用于时域迁移.具体实现步骤参见算法1.课程学习使单个神经网络可求解的时域尽可能足够大,以便使后续迁移学习获得较大的学习步长.而后续的迁移学习本质上是一种时域堆叠分解方法,它能够进一步扩大可求解的时域.

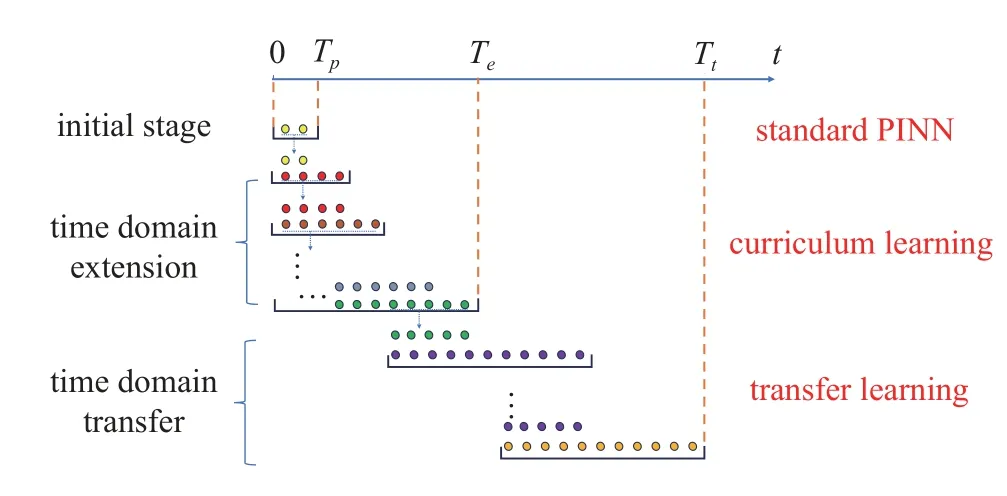
图2 课程-迁移学习物理信息神经网络求解长时间历程问题示意图Fig.2 Schematic diagram of curriculum-transfer-learning-based physics-informed neural networks for solving long-term problems

CTL-PINN 第一阶段得以实现的原因是传统PINN 方法能够训练得到良好的短时间问题的解;在获得初始阶段预训练的模型后,进入后续的课程学习和迁移学习阶段,其在某一训练步中所执行的具体操作如图3 所示,每个训练过程可视为一个独立的PINN 求解过程,课程学习和迁移学习阶段实现原理详见1.3.1 和1.3.2 节.

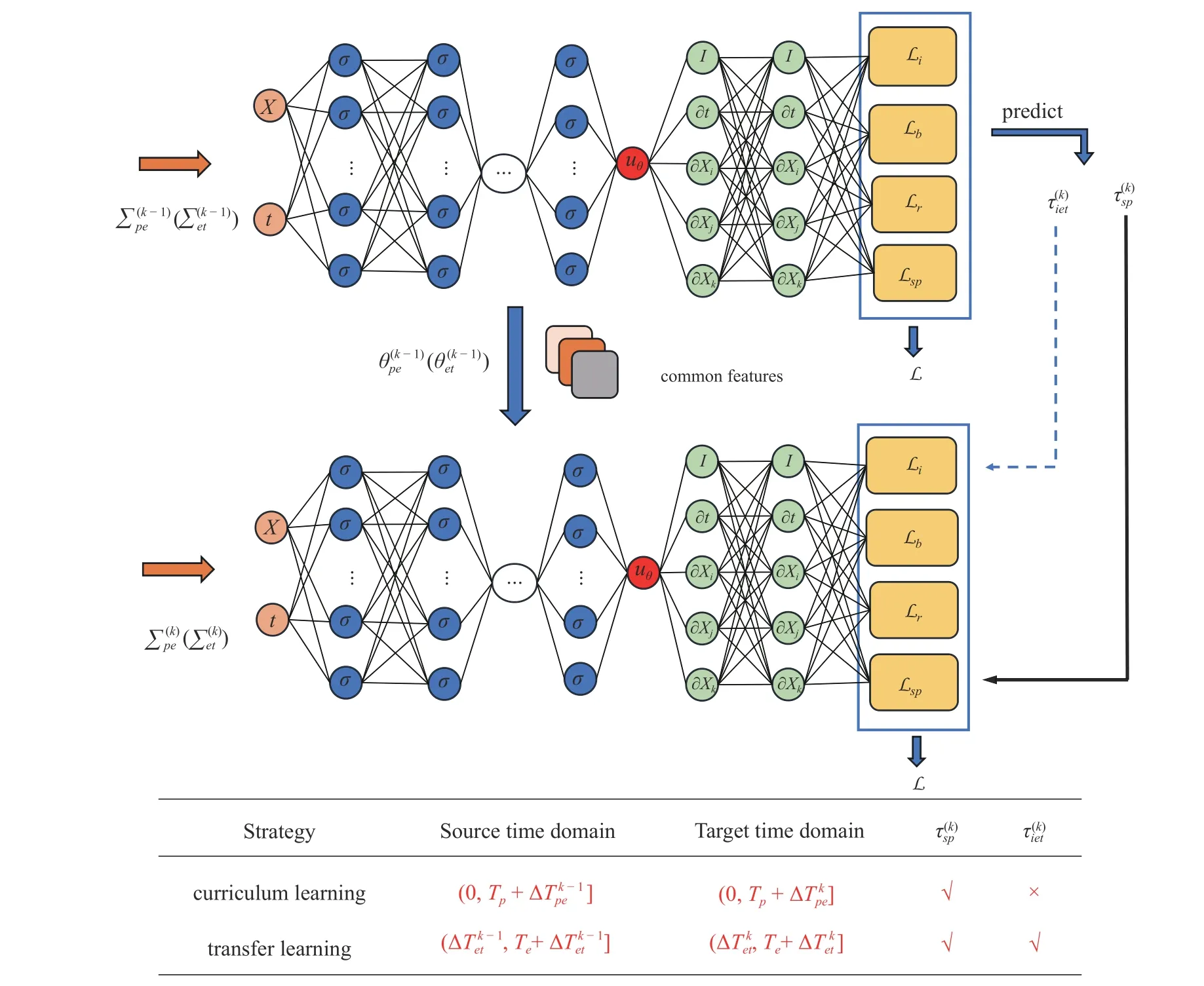
图3 在课程学习或迁移学习某一训练步中所执行的具体操作Fig.3 Specific operations performed during a training step in curriculum learning or transfer learning

1.3.1 课程学习阶段

课程学习是一种训练策略,模仿人类的学习过程,主张让模型先从容易的样本开始学习,并逐渐进阶到复杂的样本和知识[30];本研究则是基于预训练的部分中较小时域的模型,逐步扩大时域,若课程学习部分经n次时域扩大由时域 (0,Tp] 最终扩大至时域 (0,Te],扩大过程描述为

内训练完成的神经网络在 (X,t) 处的预测值,用Nsp表示额外监督学习点的数量,则额外监督学习数据集如下所示

其中损失函数如下式所示

其中wsp是额外监督学习部分的权重,Lsp是额外监督学习部分的损失,其表达式如下

在课程学习过程中,为了保证训练的准确性,扩大步长不宜过大;为了尽可能地求解更长时间的问题,使用小步长多次扩大.每次课程学习都可以扩大可求解的时域,当然,受限于单个神经网络的拟合能力,不可能一直扩大下去.

1.3.2 迁移学习阶段

迁移学习是一种机器学习技术,它可以将一个预训练模型应用于一个新的问题[31].在本研究中,以课程学习最终时域 (0,Te] 的模型为基础,将其可求解域进行迁移,若迁移学习部分经m次时域迁移后可求解域由时域 (0,Te] 最终扩大至时域 (0,Tt],迁移过程描述为

其中损失函数如下式所示

2 数值算例及讨论

本节将课程-迁移学习物理信息神经网络(CTLPINN)应用于长时间非线性波传播模拟中,并通过算例验证其有效性和鲁棒性.为了评估求解的准确性,引入L2误差,其计算方法如下式所示

本节中的所有算例都是在深度学习框架TensorFlow1.4 版本下实现的,激活函数为tanh,优化算法为L-BFGS 算法,损失函数中各部分的权重均取为1.

2.1 立方体内非线性简谐波传播

2.1.1 模型超参数讨论

超参数的选择对神经网络的训练结果有重要影响,本算例探索了神经网络的深度和宽度及残差点数量Nr对训练结果的影响.考虑以下的非线性波动方程及其对应的精确解

其中 (x,y,z,t)∈(0,1)3×(0,T],求解域为边长为1 的立方体,右端源项Q(x,y,z,t) 可将精确解代入控制方程中求得;其初始条件如下

其边界条件如下

令c=1,A=1,kx=1,ky=2,kz=3,ω=0.2π,初始点数量=200,边界条件为第一类边界条件,边界点数量=100×6=600,残差点数量Nr=1000,非线性项f(u)=sinu.采用传统PINN 方法在时域(0,30 s]内使用不同的深度和宽度的神经网络对上述问题求解,记录其L2误差,如表1 所示.

表1 在T=30 s 时不同隐藏层数和神经元个数计算结果的L2误差Table 1 L2 error with different numbers of hidden layers and neurons at T=30 s

神经网络为15 层,每层30 个神经元效果最佳;由于后续的算例中要进行时域扩大,要求神经网络有较高的拟合能力;综合考虑,在后续的算例中,神经网络模型中隐藏层数取为15,每层含有40 个神经元.图4 绘制了Nr取不同值时,其L2误差的变化;Nr=1000 时,误差趋于稳定,Nr=1200 其L2误差最小,为4.88×10-4,因此在后续的算例中Nr均取为1200.

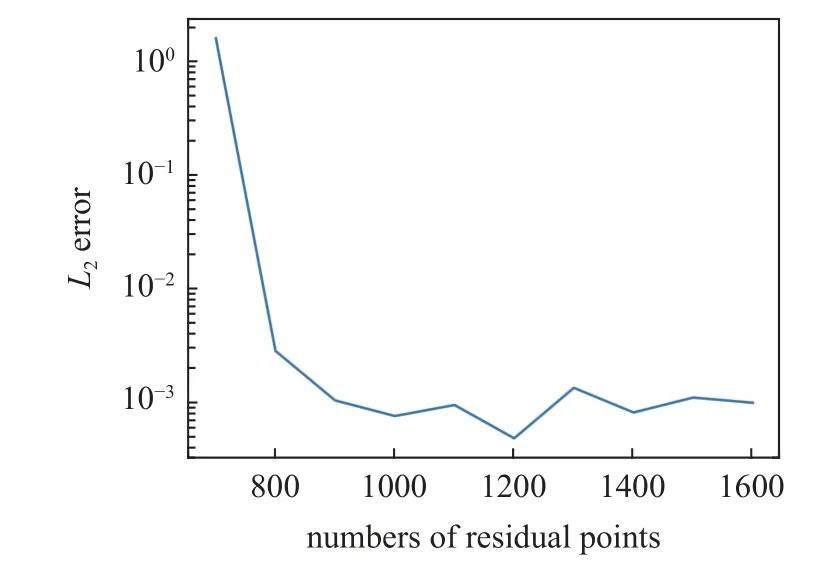
图4 不同的残差点数量对应的 L2 误差Fig.4 L2 error corresponding to different numbers of residual points

2.1.2 课程学习和迁移学习

CTL-PINN 时域扩大方法采用传统PINN 方法在时域(0,20 s]内对波动方程求解,控制方程、初始和边界条件和参数与算例2.1.1 相同,以此作为课程学习的初始模型;每次将时域扩大2 s,即课程学习步长 ∆T=2 s,课程学习额外监督学习点数量Nsp=1000,最终将可求解时域扩大为(0,100 s],即T=100 s.同时采用传统PINN 方法在时域(0,T]对波动方程求解,T依次取为20,24,28,···,96 和100 s,每次求解相互独立,参数与算例2.1.1 一致.如图5 所示,绘制出二者的L2误差随时域变化,可以发现传统PINN 方法在短时间内能够训练出高精度的结果,这也是CTL-PINN 得以实现的基础,但是随着所需求解时域的增大,其误差急剧增大且不稳定,而通过CTL-PINN 训练的结果更为精确和稳定.如图6 所示,当t=100 s 时,CTL-PINN 预测解和精确解基本一致,绝对误差在 7.0×10-3以内,说明了CTL-PINN 模拟长时间非线性波传播过程的有效性.

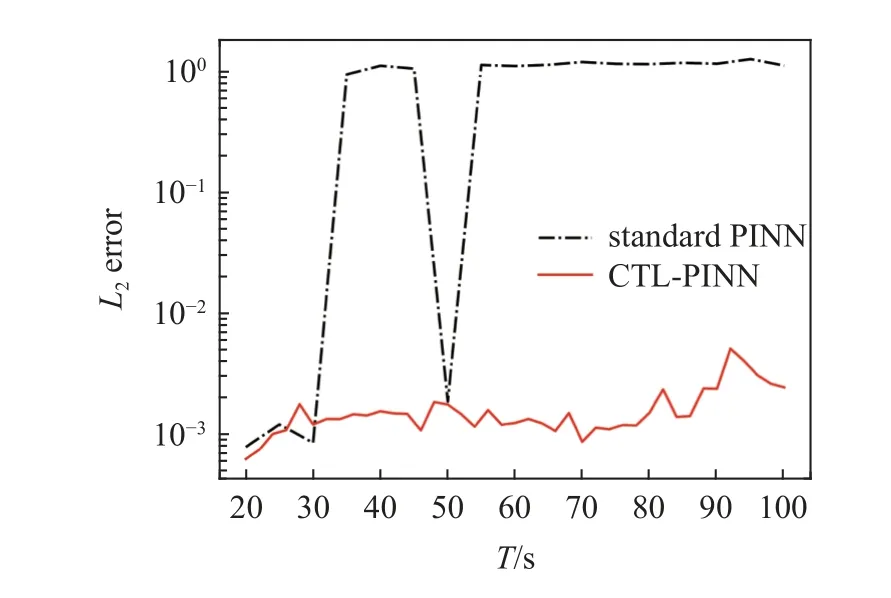
图5 传统PINN 与CTL-PINN 的 L2 误差随时域增大变化Fig.5 L2 error variation with respect to the increase of the time domain by standard PINN and CTL-PINN

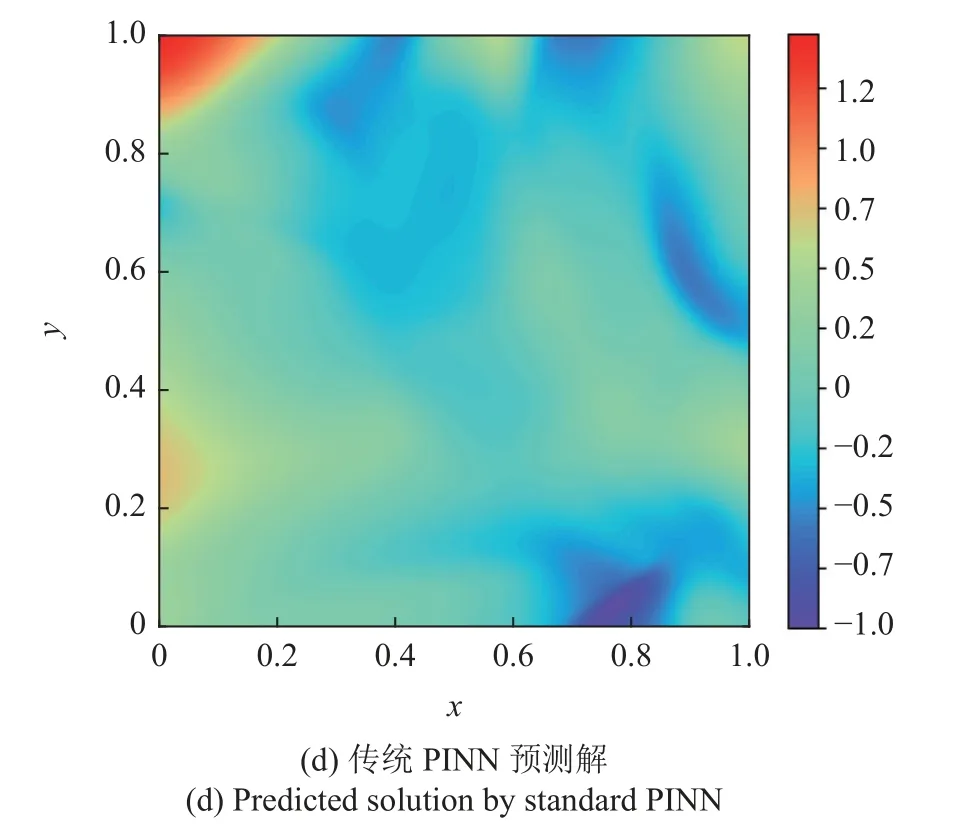
图6 当 t=100 s 时在 z=0.5 处切片,即 u(x,y,0.5,100)Fig.6 Slice at z=0.5 at t=100 s,i.e.,u(x,y,0.5,100)

图7 给出了不同课程学习步长对训练结果的影响,课程学习步长越短其训练的精度越高,推进过程中误差的变化越平稳,过长则完全无法训练,但是课程学习步长越短其在时间轴上的增长越慢,对于课程学习步长的选择需要综合考虑.

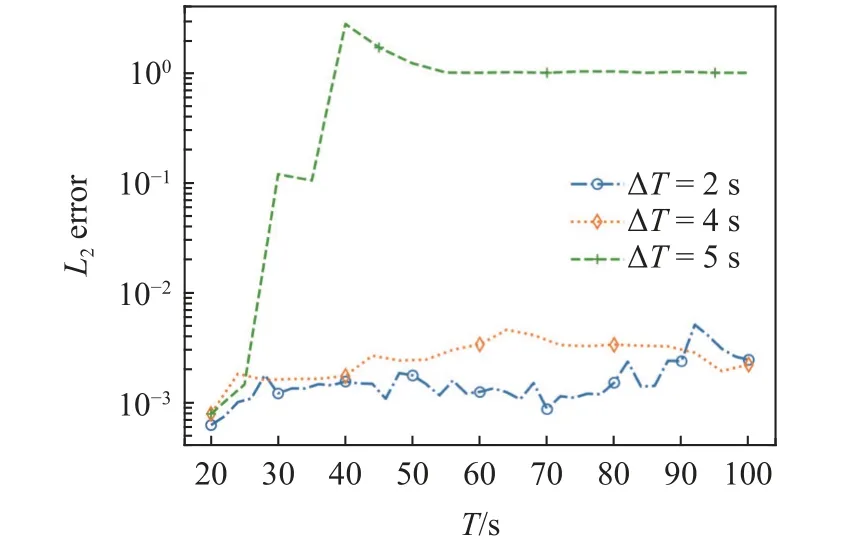
图7 不同课程学习步长CTL-PINN 的 L2 误差随时域增大变化Fig.7 L2 error variation with respect to the increase of the time domain by CTL-PINN with different time step sizes in curriculum learning stage

CTL-PINN 时域迁移方法以课程学习方法完成训练的较大时域的模型为基础模型,并使用该模型预测的中间时刻的值作为迁移后时域的初始值,并在两时域的交集的时域内均匀采样2000 个点作为额外的监督学习点.如表2 所示,不同迁移学习步长均取得了较低的误差,对于本问题,迁移学习步长以50～70 s 为宜.

表2 不同迁移学习步长对应的 L2 误差Table 2 L2 error corresponding to different transfer learning step sizes

2.1.3 其他非线性项

选取非线性项为u2,u3及eu,初始和边界条件及参数与算例2.1.2 节相同,探讨CTL-PINN 方法对不同非线性问题的适应性.如图8 所示,对于u2及u3,在100 s 以内均可较高精度地求解,二者结果绝对误差分布如图9(a) 和图9(b) 所示.而 eu在推进至88 s 处误差突然增大,由于非线性过强,无法继续再进行时域扩大.以(0,88 s]的模型作为迁移学习的基础模型,迁移学习步长为12 s,使用2 个神经网络可将求解域扩大为(0,100 s],其结果绝对误差分布如图9(c)所示,迁移学习在保持较大的学习步长的基础上进一步扩大了可求解的时域.CTL-PINN方法对不同的非线性问题都有很好的适应性.

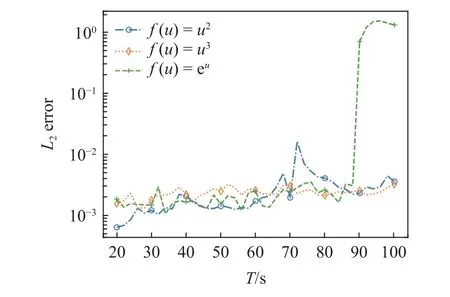
图8 不同的非线性项CTL-PINN 的 L2 误差随时域增大变化Fig.8 L2 error variation with respect to the increase of the time domain by CTL-PINN with different nonlinear terms

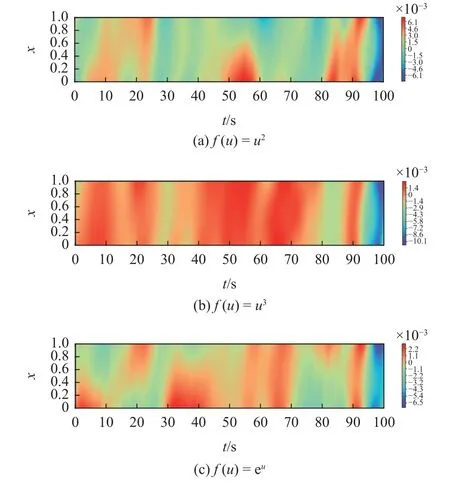
图9 在求解时域为(0,100 s]时的绝对误差分布 (y=0.5,z=0.5)Fig.9 Absolute error distributions in the time domain of(0,100 s] (y=0.5,z=0.5)

2.2 球体内非线性衰减波传播

考虑一个具有以下控制方程和精确解的非线性衰减波

其中 (x,y,z,t)∈Ω×(0,T],求解域 Ω 为半径为1 的球体,初始和边界条件满足精确解,源项可由精确解得到,边界点在球面上,数量,ω=0.3π,其他参数与2.1 节相同.

如图10 所示,相比传统PINN,CTL-PINN 训练的结果更为精确和稳定,可求解的时域更长;而对于无速度初始条件与初始和边界条件训练点数据附带1‰随机噪声这两种求解难度更高的情况,CTLPINN 亦能求解,说明了CTL-PINN 具有良好的鲁棒性.如图11 所示,衰减波在传播过程中振幅逐步减小,造成这种现象的原因通常是波的能量在传播过程中转化为热能,或者被传播介质吸收.当T=80 s时,CTL-PINN 预测解和真实解基本一致,而传统PINN 预测解和真实解相差甚远,体现了CTL-PINN处理复杂波传播问题的有效性.

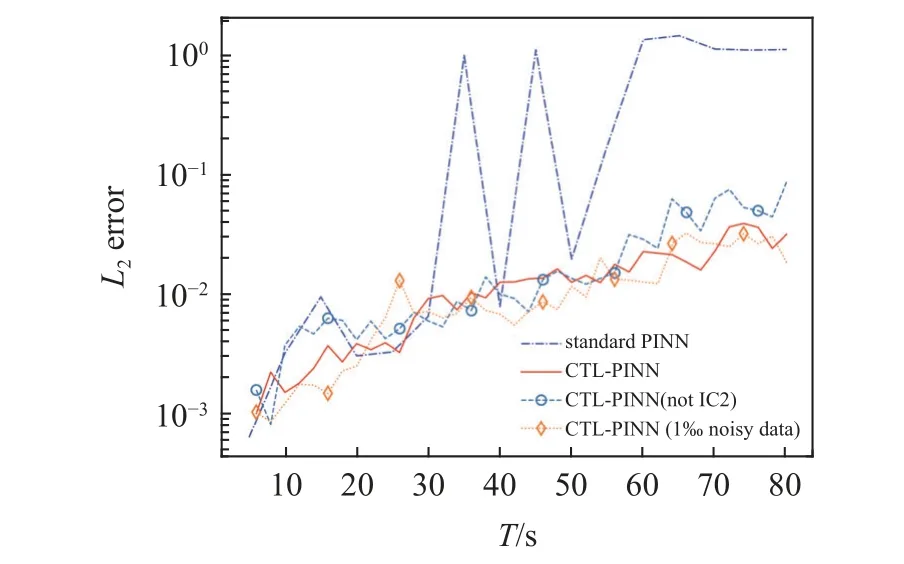
图10 传统PINN、CTL-PINN、无速度初始条件的CTL-PINN (not IC2)与初始和边界条件训练点数据附带1‰随机噪声的CTL-PINN(1‰ noisy data)的 L2 误差随时域增大变化图Fig.10 L2 error variation with respect to the increase of the time domain by standard PINN,CTL-PINN,CTL-PINN (not IC2) without velocity initial conditions and CTL-PINN (1‰ noisy data) with 1‰random noise attached to the initial and boundary conditions training point data

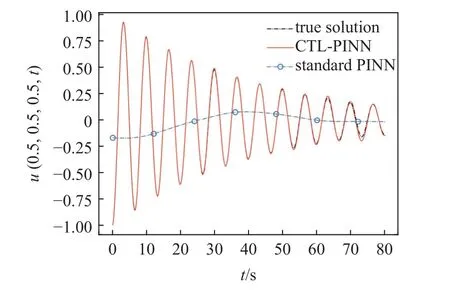
图11 在点(0.5,0.5,0.5)处的真实解、传统PINN 与CTL-PINN 的预测解Fig.11 True solution,predicted solution by standard PINN and CTLPINN at point (0.5,0.5,0.5)

2.3 无源项的非线性波传播

上述2 个算例证明了CTL-PINN 在模拟长时间非线性波传播过程的有效性和鲁棒性.本算例除去源项,研究非线性项的强弱对波传播的影响,其控制方程如下所示

图12 不同的非线性项系数 λ 在点(0.5,0.5,0.5)处的CTL-PINN 的预测解Fig.12 Predicted solution by CTL-PINN at point (0.5,0.5,0.5) for various nonlinear term coefficients λ

3 结论

本文提出了课程-迁移学习物理信息神经网络,有效地解决了传统物理信息神经网络在长时间历程模拟中存在的计算稳定性差和无法获得有效解的问题.通过将长时间历程模拟问题转化为若干个短时间历程模拟子问题,并结合课程学习和迁移学习技术,实现了长时间非线性波传播模拟.此外,本文方法还利用当前步物理信息神经网络训练得到的神经网络参数及额外监督学习点信息,避免了传统物理信息神经网络陷入局部最优解的问题.通过几个基准算例的验证,证明了本文方法在模拟长时间非线性波传播过程中的有效性和鲁棒性.

(1) CTL-PINN 方法可以获得比传统PINN 方法更精确的解,并且可以求解更长的时域.然而,由于需要反复导入模型进行训练,其训练时间较长.如何在增大学习步长的同时保证精度,是一个必须考虑的问题.为了解决这个问题,可以在后续研究中开发步长自适应算法,采用并行技术以提高训练效率.

(2)额外监督学习点可以提升神经网络的训练效果,但是由于额外监督学习的数据是由神经网络预测得到,其与精确值之间存在一定误差,会导致一定的误差累积.

(3)本文对非线性波传播正问题进行了求解,后续可在此基础上进一步将该算法拓展到反问题.