平行轴涡动黏性充液转子动力稳定性计算和影响因素分析1)

王 威 王维民 ,*2) 任映霖 王珈乐 李维博

* (北京化工大学高端压缩机及系统技术全国重点实验室,北京 100029)

† (北京化工大学高端机械装备健康监控与自愈化北京市重点实验室,北京 100029)

** (北京化工大学发动机健康监控及网络化教育部重点实验室,北京 100029)

引言

高速离心机是核工业、化工、生物、医药等国防工业领域和国民经济产业领域的关键技术装备,尤其在核能领域,高速离心机广泛应用于提纯放射性乏燃料,对于提高乏燃料利用率、降低核废料污染以及保障我国核电可持续发展具有重大战略意义.在一定条件下当充液转子发生扰动时,腔内旋转液体被激起扰动运动,二者发生耦合,诱发转子自激失稳[1],并且在某一较宽转速区间内转子始终呈现出失稳状态[2-4].在失稳转速区间内转子以极大的振动作异步涡动,这严重制约了充液转子向高速化、大型化方向的发展.

采用减振装置来减小液体激励导致转子失稳的不利影响是充液离心机转子振动控制中常用的技术手段,其中黏弹性橡胶材料生产成本低廉且具有较好的耗散作用,被广泛用于各类减振与降振系统中.赵云飞[5]、窦逸飞[6]和郝泽睿[7]建立了非充液状态下的转子-基础耦合有限元动力学模型,揭示了基于动力吸振原理下的弹性基础刚度、橡胶阻尼对系统固有频率和转子振动抑制的作用规律.Derendyaev等[8-10]建立了单跨内充液的Laval 转子模型,研究了不同充液黏性和支承各向异性下的系统稳定性问题,并提出了一种不同于传统的D 分解的稳定性判据.Zhang 等[11]首次提出了气泡动力学方程,针对液体运动过程中因空化而形成气泡,建立了全新的振荡气泡动力学理论并开展实验研究,对其理论模型进行了验证,该理论不仅统一了不同的经典气泡方程,同时该方程保持了统一而优雅的数学形式.

在考察部分充液转子的动力稳定性时,如何计算液体作用在转子内壁上的扰动流体力是关键一步[12-14].与此同时在理论分析中,流体的黏性以及转子系统的外阻尼在转子系统稳定性边界的判定中扮演重要角色.在未考虑流体黏性的模型中,外阻尼是导致充液转子失稳的关键因素[15-16],而实际上流体均具有一定的黏性,分析转子的稳定性时引入外阻尼而不考虑流体黏性是不充分的[16];在考虑流体黏性的模型中,通过增大外阻尼能够很好抑制充液转子的失稳[16-20],需要注意的是当流体(例如水)的黏度较低时,充液转子的失稳转速区间随外阻尼的增大而保持不变[19].

针对特定类型的充液转子,例如轴向长度较深的转鼓、油井钻杆等模型,其涡动中心与转子自转中心并不重合,直接结果是产生陀螺效应并且改变了腔内液体沿轴线方向的分布规律.为了完整体现流体与转子之间的相互耦合作用,此时需要建立三维计算流体动力学模型.流场计算完成后的处理思路有:(1) 完整计算出作用在转子上的集中力和集中力矩,耦合到转子动力学方程中进一步分析转子的失稳边界,分析结果表明陀螺刚化效应以及由于流体运动产生与转鼓倾斜方向相反的力矩均能够提高转子稳定性的上下边界[21];(2) 计算出流体扰动力沿轴线方向分布规律,此时流体力以分布力的形式耦合到转子动力学模型中,进而分析充液转子的稳定性,研究发现流体压强与转子的挠曲变形之间存在着非常复杂的非线性关系[22-26],把油井钻杆这一类型的柔性充液转子视为刚性转子分析是不合理的.

如何求解纳维-斯托克斯方程并且耦合到转子动力学方程是必不可少的步骤.Wang 等[24]和袁惠群等[27]推导了无量纲形式纳维-斯托克斯方程,采用解析解的方式求解了流体激振力,根据哈密顿原理推导了耦合流体激振力的转子动力学方程,并进行了无量纲化处理,研究了不同支撑刚度、充液比、质量比和雷诺数等对充液转子稳定性的影响,结果表明与本文结论一致,支撑刚度的变化对充液转子失稳转速区间的影响并不明显;Sahebnasagh 等[28]建立了含有两种不同理想液体的充液转子的纳维-斯托克斯方程,并运用解析解的方法分析了这一类型充液转子的稳定性,结果表明与充有一种液体的转子相比,充有两种不同液体转子更易失稳.Firouz-Abadi 等[29]基于不可压缩流体的纳维-斯托克斯方程,为圆柱体各部分的液体运动建立了二维模型,并以解析解求得施加在圆筒壁上的液体压力,将旋转圆筒的振动与液体运动相结合,得到液固耦合转子动力学模型,确定了系统不稳定的条件.

研究充液转子动力稳定性的另一个重要手段是实验,并且充液转子的不稳定现象最早也是通过实验发现的[2].实验分析表明,充液转子的稳定性是充液比、流体黏性、系统刚度以及外阻尼等众多因素共同决定的[30-32].首先,对充有高黏度流体的转子系统,理论分析中必须采用黏性流体模型;其次,充液比增大转子系统的不稳定区明显减小;第三,充液转子在加速和减速通过不稳定区时,转子的运动不具唯一性,前两点与理论分析具有一致性.

本研究工作以平行轴涡动黏性充液转子为研究对象,流体动力学方程中忽略流体的重力以及表面张力的影响,同时假定流场内各物理量沿液盘轴向是均一的.采用有限差分法求解流体动力学方程,耦合转子动力学方程并以状态空间法降阶求解出特征值,根据方程的特征根进而判定黏性充液转子的动力稳定性,并针对不同充液比、黏性、刚度和阻尼等参数下的稳定性特性进行讨论,为充液离心机转子的增稳设计与减振调控提供了新思路.

1 流体运动控制方程

1.1 流体动力学方程

如图1 所示,充以部分不可压缩黏性液体的中空液盘装配于弹性轴的中间,转子的自转角速度恒定为 Ω,并以未知角速度 ω 围绕转子中心轴线涡动,扰动振幅表示为

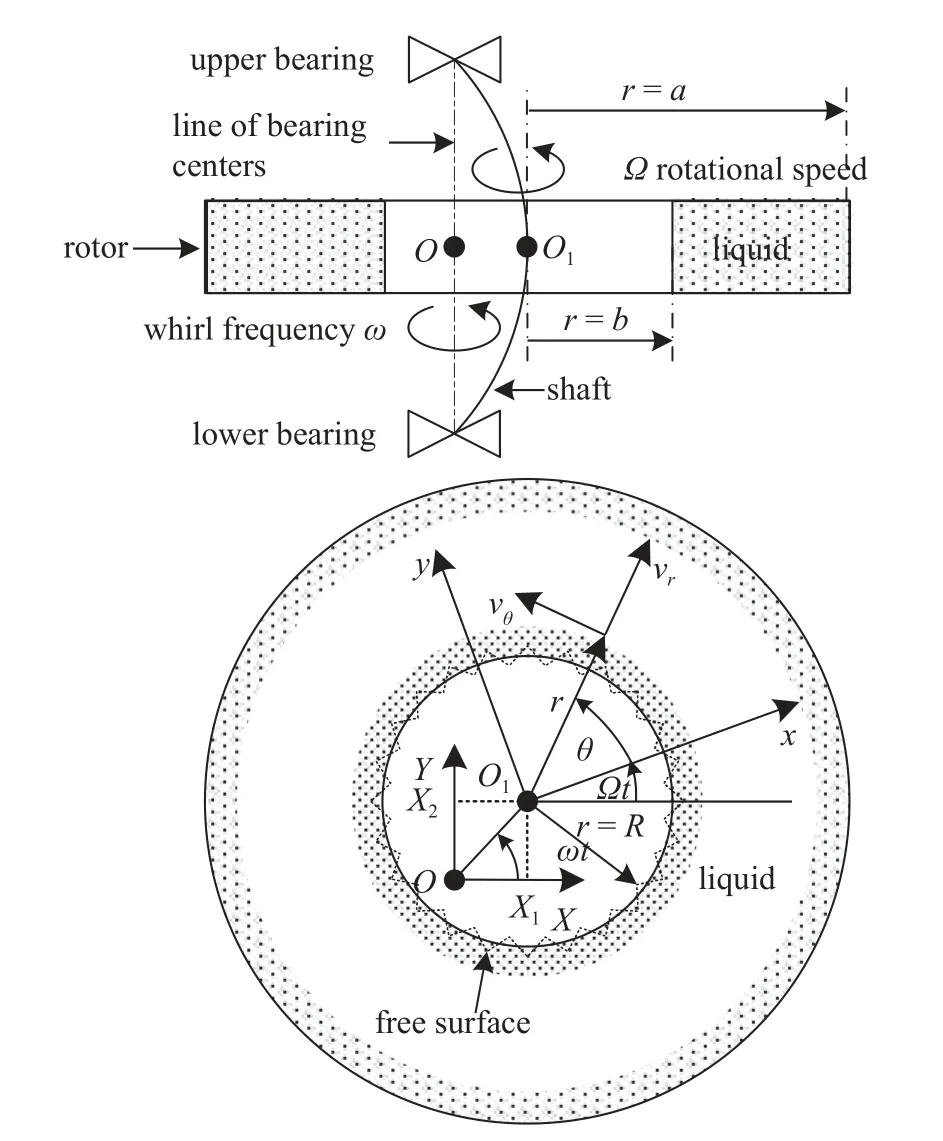
图1 部分充液转子Fig.1 Rotor partially filled with liquid

其中,λ=σ+jω,σ 为阻尼衰减指数(未知),ω 为涡动频率(未知),j2=-1 .由于转子的涡动,在流体的动力学方程中需引入强迫项,该强迫项在液体层中产生激励,而激励又作用于液盘的内壁,该激励力与维持液体运动所需要的力大小相等方向相反,该激励力可以表示为转子旋转速度 Ω 和涡动频率 ω 的函数,将该激励力耦合到转子的运动方程中,当 ω 同时满足流体动力学方程和转子动力学方程,方程求解完成,同时将得到的衰减阻尼指数 σ 求对数衰减率便可判断出稳定性.采用扰动位移X1和X2可以将液体的自由表面表示为

其中,b是无扰动时旋转液体在离心力作用下的自由表面,R是有扰动时旋转液体的自由表面,Φ1和Φ2是扰动发生后液体自由表面的响应函数.在图1中,直角坐标XOY是固定坐标系,直角坐标xO1y和极坐标系rO1θ是随液盘转动坐标系,因此在转动坐标系rO1θ下液体层的动力学方程为

其中,vr和vθ分别是流体微元沿着极坐标径向r方向和周向θ方向的速度分量,p是流体压强,ρ是流体密度,ν 是流体的运动黏度.方程右端最后一项表示转子涡动产生的转动坐标系的加速度.

1.2 连续性方程

根据质量守恒,在二维转动坐标系rO1θ中,不可压缩牛顿流体的连续性方程可以表述为如下形式

1.3 边界条件

在二维转动坐标系rO1θ中,液盘的内壁面上,即r=a处,流体径向速度和切向速度为0 (无滑移)

其中,a表示液盘内壁面半径.在液体的自由表面上,即r=R处,流体压强为0

其次,在液体的自由表面上,即r=R处,液体自由表面有微小扰动,流体的径向速度为

R是在式(2)中定义的扰动后流体的自由液面,在微小扰动下近似认为

第三,在液体的自由表面上,即r=b处,流体沿周向的剪切力为0

其中,μ=ρν是流体的动力黏度.对于不可压缩黏性流体,边界条件式(9)可以改写为

因此,腔内流体完整的边界条件可以逐一表示为

2 流体运动控制方程求解

2.1 流体动力学方程线性化

流体动力学方程(3)是非线性方程,因此无法通过解析法得到该方程完整的解.在这里我们参考Wolf[3]的求解办法,采用扰动法对方程(3)进行线性化,其中扰动参数为转子的扰动位移X1和X2,并且忽略高阶项

在稳态条件下,无扰动时有

为了使流体动力学方程(3) 在扰动方向X1和X2上解耦,在此引入6 个辅助变量[3],分别如下

因此,可以反解出扰动方向X1和X2上的扰动速度和扰动压力

将式(12)、式(13)和式(15)代入式(3)中可以得到稳态条件下和扰动条件下的6 个动力学方程

其中,α=λ+jΩ,β=λ-jΩ .同理,根据质量守恒

将式(12)、式(13)和式(15)代入式(11),可以得到以辅助变量表示的完整边界条件

2.2 扰动方程解耦

在文中,扰动速度和扰动压力同时是时间和空间(坐标)的函数,为方便计算,需要将时间和空间解耦分离,因此辅助变量可以表述为

将式(19)代入式(16b)～式(16d)和式(17),可以将该问题转换为两个解耦方程的边值问题,解耦后的方程为

其边值为

显然,式(21)表示的4 组边值与式(18)表示的4 组边界条件是逐一对应的.式(20)是一组4 阶线性齐次常微分方程组,其通解中包含第一类和第二类Bessel 函数,并且第一类和第二类Bessel 函数均出现于通解的虚部,造成函数容易出现极端梯度.采用有限差分数值计算手段很好地解决了这一求解难题.

2.3 有限差分法求解动力学方程

式(20)和式(21)描述了扰动速度和扰动压力满足的微分方程以及边界条件,并且当采用文献[3]所提到方法,对原流体速度和流体压强进行时空解耦分离后,可以看出辅助变量均是关于径向坐标r的一元函数,与时间项无关.我们将液体层沿着半径方向划分为n个单元,一共产生n+1 个节点.下面我们用有限差分表示微分方程中的各阶微商,在单元的内部节点上采用中心差分公式表示各阶微商,一元函数的前4 阶中心差分公式为

其中,i=2,3,···,n-2,为各节点的函数值,单元长度为 ∆r=(a-b)/n.式(20)的微分方程可以写作差分格式

在式(23)中方程的各项系数为

其中,ri是各节点的径向坐标,i=2,3,· ··,n-2 .式(23)给出了求解域内部各节点需要满足的线性方程组(微分方程转化为线性方程组),对于边界上的节点则需要满足边界条件,即需要满足式(21),由于边界条件中存在导数,而在边界上只能用单侧有限差分表示各阶微商,一元函数的前3 阶单侧有限差分公式分别为

将式(25)代入到式(21),有对应的4 组边界条件

将式(24)和式(26)改写为矩阵形式

3 流体激励力的积分运算

采用计算机程序求解式(23)和式(26)便可计算各节点的函数值.将节点函数值回代到式(9)和式(12)便可计算液体层各坐标位置的流体压强以及流体剪切力,需要计算作用在液盘内壁面上的流体力,就需要对压力和剪切力做数值积分运算,此时,取径向坐标r=a,则在直角坐标xO1y中作用在液盘内壁面上的流体净力为

其中,L是液盘的轴向长度.上述积分运算的计算量较大,此处不详细推导,在此给出关键性的计算结论

其中

式中ml=ρπa2L是充满液盘内腔时液体的全部质量.

直角坐标xO1y是随盘转动坐标系,为了建立转子在平衡位置的动力学方程,需要得到固定坐标系XOY下的流体力分量,根据坐标变换关系有

因此,可以将式(32)和式(33)均代入式(34)

4 转子动力学方程的建立及方程降阶

在得到流体激励力后,可以在固定坐标系XOY下建立转子动力学方程

在式(38)中,mr是未充液时空转子的质量,cX和cY为主阻尼系数,kX和kY为主刚度系数.因此,转子动力学方程式(37)可以重新写作

针对式(39) 我们采用状态空间法对其进行降阶,转化为一般性的特征值求解问题,进而计算转子系统的涡动频率 ω (阻尼固有频率)和阻尼衰减指数σ,与所有的稳定性判定结论一致,当阻尼衰减指数σ<0 时,整个转子系统是稳定的;当阻尼因子 σ≥0时,转子系统是非稳定的.采用状态空间法降阶处理后的常微分方程为

经过上述降阶处理后,便可采用现有计算标准特征值问题的求解方法计算其特征值

需要注意的是,在本问题中流体动力学方程和转子动力学方程相互耦合,无法预先知道特征值 λi,因此上述求解过程是一个循环迭代过程,当收敛精度满足要求后,求解结束.其一般思路是:

(1) 猜想特征值 λ 代入流体动力学方程式(3);

(2) 经过整理后,式(23)和式(26)表示的边值问题便可采用有限差分法求解,进而计算作用在液盘上的流体激励力;

(3) 步骤(2)完成后,则A+B和A-B的值均可计算,此时利用式(41)便可计算特征值 λi;

(4) 步骤(3)计算得到的特征值一共是4 个,可分为两组,每一组以共轭复数的形式成对出现,我们取实部最大的特征值记为 λmax,当前后两次计算特征值的二范数满足收敛精度(<10-4),σmax即为判断稳定性的特征值实部;当未达到收敛精度时,把特征值 λmax赋值给步骤(1)中的 λ 继续迭代.

5 稳定性计算结果讨论

由于黏性充液转子的稳定性是由多个参数控制决定的,因此,我们定义了以下几个变量

式中 ωX为空转子的一阶固有频率.

式中S为无量纲角频率,简称频率比.

式中c为无量纲阻尼系数,表征X和Y方向外阻尼大小.

式中k为无量纲刚度系数,表征X和Y方向外刚度的大小.

式中P描述液盘中存在液体量的物理量,P=1 时表示空转子;P=∞ 时表示液盘中充满液体.为在整个转速区域内全面了解不同黏性、充液比、刚度和阻尼对系统稳定性的影响,最大阻尼衰减指数 σmax为频率比S的函数.

离心机的液盘结构如图2 所示,离心机结构参数及液体的物理参数如表1 和表2 所示.

表1 离心机结构参数Table 1 Centrifuge structural parameters

表2 液体的物理参数Table 2 Liquid physical parameters

图2 离心机液盘结构Fig.2 Centrifuge liquid tray structure

图3(a)给出了在不同黏度条件下特征值的实部最大值 σmax随频率比S的变化曲线,图3(a)中不同黏度等级代表液盘中充以不同运动黏度的润滑油,例如,黏度等级为ISO VG 22 表示液盘充以室温下平均运动黏度为 22 mm2/s 的润滑油.根据稳定性判据 σmax≥0 是非稳定区,σmax<0 是稳定区可知,随着润滑油的黏度增大,不稳定下边界左移,不稳定上边界右移,同时峰值增大,即充液转子的稳定区间减小,非稳定区间增大,这一计算结果与Holm-Christensen 等[16]的结论一致;其次,在高黏性的条件下,充液转子存在一个较宽的非稳定转速区间.由此可见,降低液盘中液体的黏性有利于提高转子的稳定性.

图3(b)为不同充液比P对转子系统稳定性的影响,对比P=1.67,P=1.82 和P=2.003 个不同充液量的工况,在失稳区间内,最大阻尼衰减指数 σmax随着充液量的增大(P增大)而减小,即不稳定的下边界右移,不稳定上边界左移,同时峰值降低,即充液转子的稳定区间增大,非稳定区间减小.该计算结果与祝长生[32]的实验结论吻合,其实验结果表明在较小充液量工况下,转子系统的非稳定区较宽,转子在非稳定区内的振动很强;对于较大充液量工况,转子的非稳定转速区间明显减小,转子在非稳定区间的振动很弱.

图3(c) 是轴承处不同主刚度k对转子系统稳定性的影响,对比k=10 MN/m,k=50 MN/m 和k=90 MN/m 3 种不同主刚度的工况,在失稳区间内,最大阻尼衰减指数 σmax随着主刚度k的增加而减小,即不稳定的下边界右移,不稳定上边界左移,同时峰值降低,即充液转子的稳定区间增大,非稳定区间减小.其次,可以看出充液转子的最大阻尼衰减指数 σmax的变化随轴承处主刚度值的改变并不明显,这与袁惠群等[27]的计算结果一致,因此,通过增加轴承处主刚度使充液转子增稳具有局限性.

外阻尼比c对充液转子系统稳定性的影响是另一个重要的影响因素,研究发现在各种无黏性充液转子模型中引入外阻尼,部分充液转子在任何转速下均是非稳定的.Hendricks 等[17]给出的解释是,外阻尼力与转子的加速度具有相位差,无黏性流体无法抵消该阻尼力.图3(d)给出了不同外阻尼比c对转子系统稳定性的影响,首先,在整个转速区间内最大阻尼衰减指数 σmax随频率比S的变化规律与图3(a)～图3(c)所示的变化规律均一致,在 1 .1S附近(左边和右边)出现两个峰值.其次,在整体转速区间内,最大阻尼衰减指数 σmax随着外阻尼比c的增加而减小,即不稳定的下边界右移,不稳定上边界左移,同时曲线整体向下移动,即充液转子的稳定区间增大,非稳定区间减小;当c=0 (无外阻尼)时,整个转速区域内不存在稳定转速区间.与前面3 个影响因素(黏性、充液比和主刚度)明显不同,外阻尼c能够从整个转速区域内降低最大阻尼衰减指数 σmax,提高充液转子系统的稳定性.

为突出本研究中图3 所示的结果所表述的规律更具有一般性,增强本研究结论的说服力,在图4 中计算了多工况下黏性充液转子失稳转速边界随流体黏性、充液比、轴承刚度和主阻尼等参数的变化规律.当黏性充液转子的工作转速落入边界BC1 和BC2 之间或者边界BC3 和BC4 之间时,黏性充液转子出现失稳,工作转速落在该区域以外时,转子充分稳定.此外,在转子的一阶临界转速以上均存在两个失稳转速区间,除轴承刚度以外,流体黏性、充液比和主阻尼的失稳边界存在交点,即是说通过参数调整,黏性充液转子失稳转速区间可以消除.

图4 不同参数对系统失稳转速区间边界的影响Fig.4 Influence of different parameters on the boundary of the unstable speed range of the system

图4(a)表明当充液转子的液体黏度增大,转子系统的失稳转速区间逐渐变宽,该现象说明当流体黏度等级处于ISO VG 22～ISO VG 46 之间时,降低流体黏性有利于转子趋于稳定.

图4(b)表明当充液转子的充液量(1/P减小)增大时,转子系统的失稳转速区间逐渐变窄,转子稳定性增强,并且当充液比的倒数1/P小于0.55 时,不存在失稳转速区间.

图4(c)表明当改变轴承刚度(107～108N/m)时,转子系统的失稳转速边界会随之一起改变,但是失稳转速区间宽度不发生明显变化,通过参数调节难以将失稳转速区间消除.

图4(d)表明当增加主阻尼时,转子系统的失稳转速区间逐渐变窄,转子的稳定性增强,并且当主阻尼系数大于6 N·s/m 时,转子系统的失稳转速区间消失,此时启停转子,转子不会出现失稳.

图5 给出了不同参数对系统稳定性影响的瀑布图,该图能够更为清晰直观地反映不同参数变化时,系统稳定性随各参数值变化的梯度大小和线性程度;不稳定区间在频率比区间上的具体位置变化、不稳定区间的宽窄变化等特性.

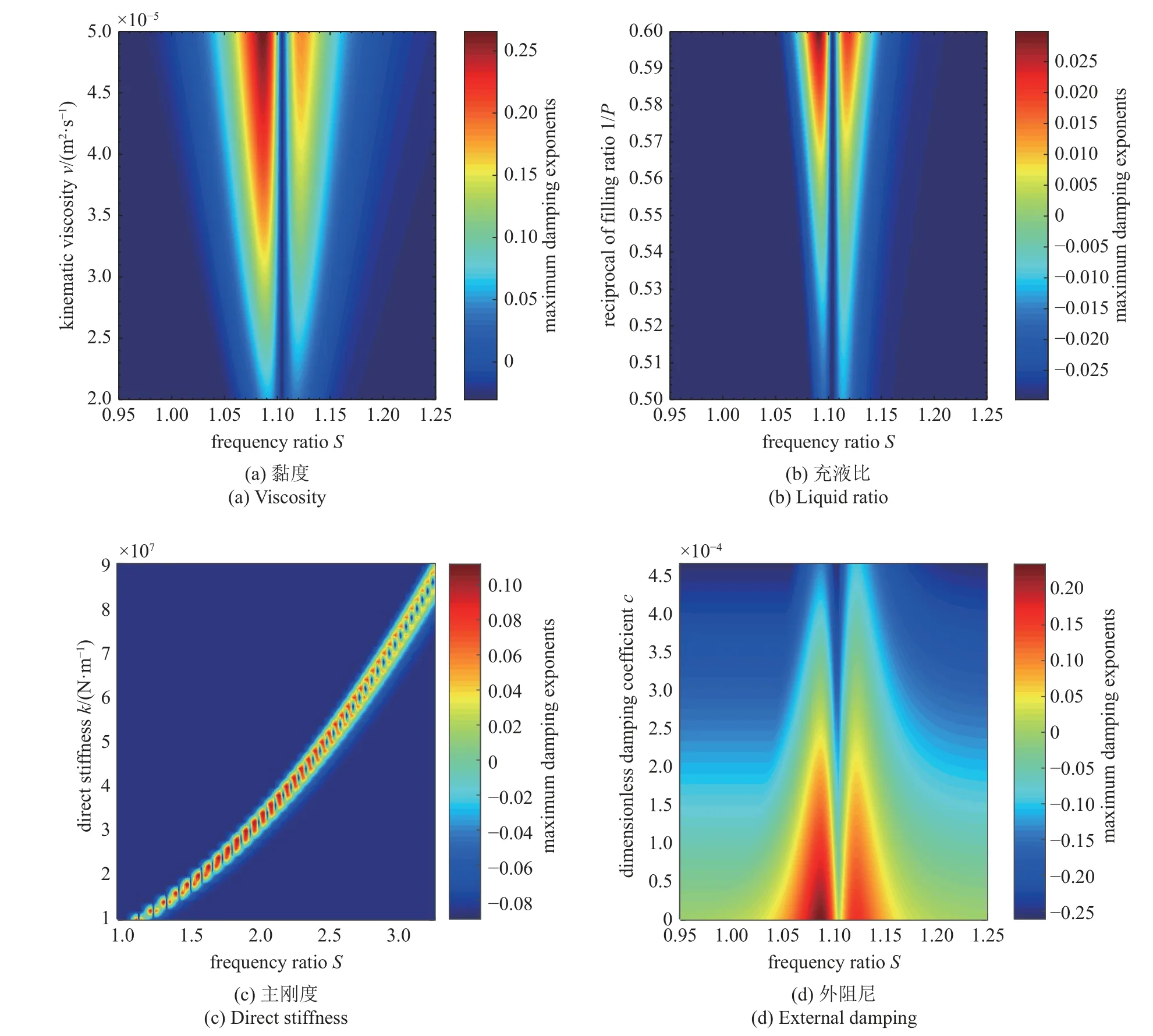
图5 不同参数对系统稳定性影响的瀑布图Fig.5 Waterfall diagram of influence of different parameters on system stability

从图5 中除了能得出图3 结论以外,还有如下规律与结论:图5(a)表达了最大阻尼衰减指数 σmax随运动黏度 ν 的变化规律,当运动黏度 ν 增大时最大阻尼衰减指数 σmax峰值随之呈非线性增大,最大阻尼衰减指数 σmax峰值梯度变化缓慢,即充液转子稳定性降低,同时不稳定区间的位置不变,但范围变宽.

图5(b)表达了最大阻尼衰减指数 σmax随充液比P的变化规律,当充液比P增大时最大阻尼衰减指数 σmax峰值随之呈非线性减小,最大阻尼衰减指数 σmax峰值梯度变化迅速,即充液转子稳定性增强,同时不稳定区间的位置不变,但范围变窄.

图5(c)表达了最大阻尼衰减指数 σmax随主刚度k的变化规律,当主刚度k增大时最大阻尼衰减指数 σmax随之呈非线性减小,最大阻尼衰减指数 σmax峰值梯度变化缓慢,即充液转子稳定性增强,但是刚度调节的优点在于能够改变不稳定转速区间的位置.

图5(d)表达了最大阻尼衰减指数 σmax随外阻尼c的变化规律,当外阻尼c增大时最大阻尼衰减指数 σmax峰值随之呈线性减小,即充液转子稳定性增强,同时不稳定区间的位置不变,但范围变窄.

对比分析可知,4 个参数对于充液转子的稳定性均具有一定的调节能力,其中充液比调节和外阻尼调节具有大梯度变化特征,主刚度调节梯度变化虽然较小,但是能够改变不稳定转速区间,因此,这3 种调节方式对于充液转子增稳均具有一定工程价值.

在文中我们继续深入研究了黏性、充液比、主刚度和外阻尼造成充液转子失稳的原因.图6 所示是不同黏性、充液比、主刚度和外阻尼工况下液盘中液体产生的等效交叉刚度 I mag(A-B) 随频率比S的变化曲线.为了便于分析,图3～图5 与图6 一一对应,通过对比分析可以看出,最大阻尼衰减指数σmax与等效交叉刚度 I mag(A-B) 随频率比S的变化同步,当等效交叉刚度 Imag(A-B) 增大时,最大阻尼衰减指数 σmax也随之同步增大,在 1 .08S处最大阻尼衰减指数 σmax和等效交叉刚度 I mag(A-B) 同时第一次达到最大值,随后二者迅速同步减小,在 1.1S处等效交叉刚度 I mag(A-B) 为零,最大阻尼衰减指数 σmax降到最小,此时流致失稳现象消失;当等效交叉刚度 I mag(A-B) 反向迅速增大时,最大阻尼衰减指数 σmax也随之迅速同步增大,在 1 .12S处最大阻尼衰减指数 σmax和等效交叉刚度值 Imag(A-B)同时第二次达到最大值,随后二者同步减小.从图6 这4 幅图中可以看出,充液转子系统的交叉刚度受到黏度、充液比、主刚度和外阻尼的影响,并且交叉刚度与最大阻尼因子的变化规律具有同步性,因此,交叉刚度增大是造成充液转子失稳的重要因素.

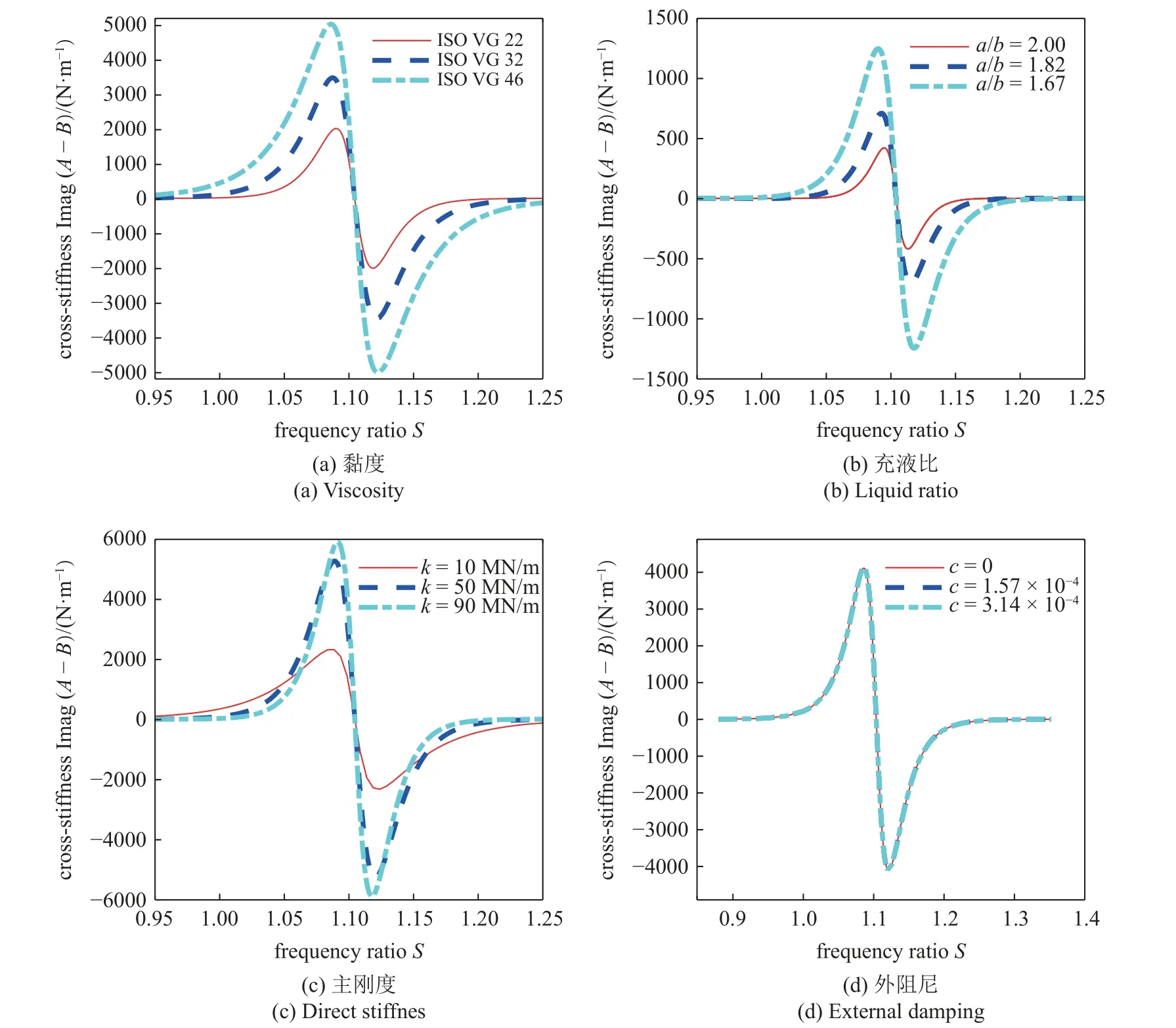
图6 不同参数对交叉刚度的影响Fig.6 Influence of different parameters on cross stiffness

图7 给出了不同参数对系统交叉刚度影响的云图,除了能得出图6 结论以外,还有如下规律与结论:图7(a)表达了交叉刚度 I mag(A-B) 随运动黏度ν 的变化规律,当运动黏度ν 增大时交叉刚度Imag(A-B) 随之增大,同时交叉刚度在转速区间上的范围变宽,对比图5(a) 这与最大阻尼衰减指数σmax随运动黏度 ν 的变化规律呈现一致性,即运动黏度 ν 增大,交叉刚度值 I mag(A-B) 增大,最大阻尼衰减指数 σmax增大,充液转子系统的稳定性降低,非稳定转速区间增大.

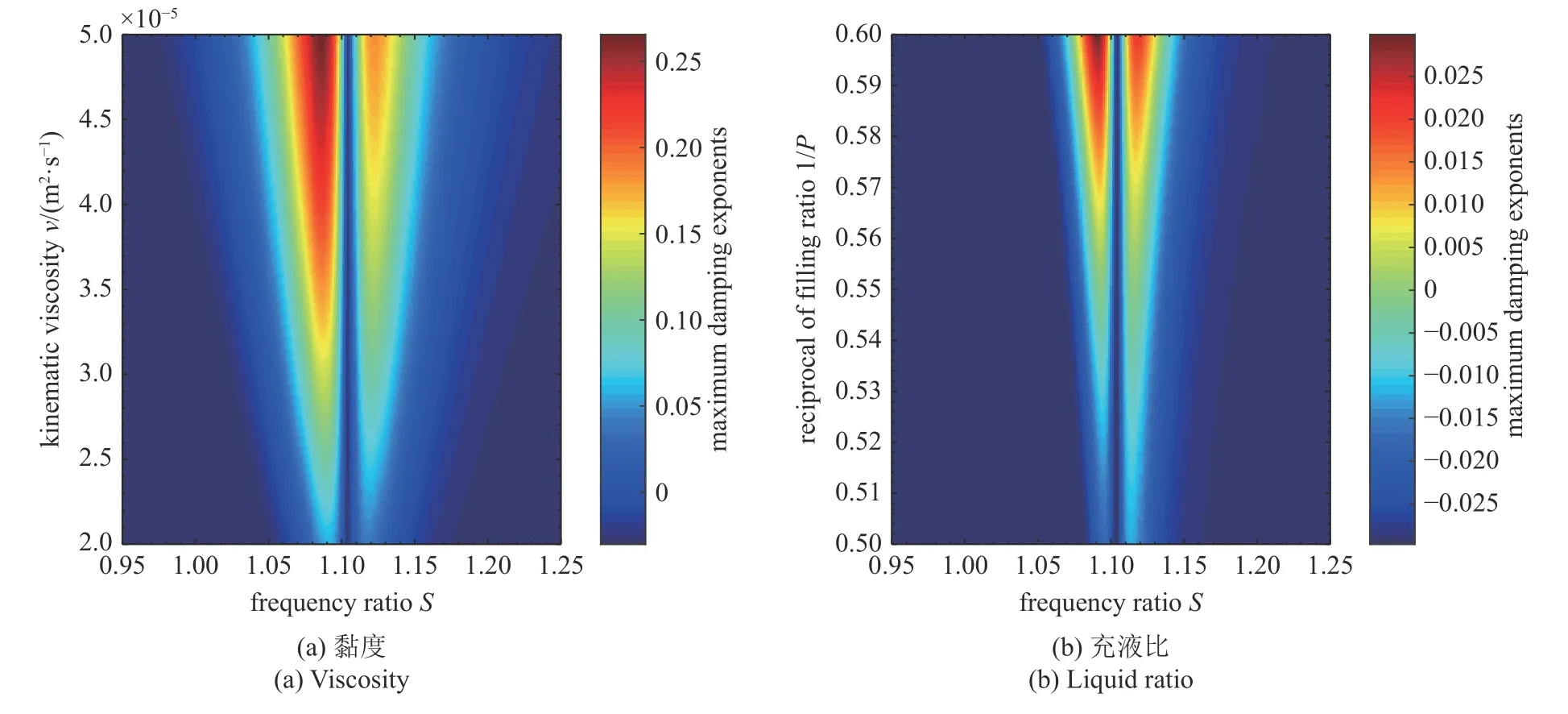
图7 不同参数对交叉刚度影响的云图Fig.7 The contour of the influence of different parameters on cross stiffness

图7(b)表达了交叉刚度 I mag(A-B) 随充液比P的变化规律,当充液比P增大时交叉刚度 Imag(A-B)随之减小,同时交叉刚度在转速区间上的范围变窄,对比图5(b)这与最大阻尼衰减指数 σmax随充液比P的变化规律呈现一致性,即充液比P增大,交叉刚度值 I mag(A-B) 减小,最大阻尼衰减指数 σmax减小,充液转子系统的稳定性升高,非稳定转速区间减小.

图7(c)表达了交叉刚度 Imag(A-B) 随主刚度k的变化规律,当主刚度k增大时交叉刚度 Imag(A-B)随之增大,同时交叉刚度在转速区间上的范围变宽,对比图5(c),这与最大阻尼衰减指数 σmax随k变化的规律相反.虽然主刚度调节转子稳定性具有局限性,但是由于其能够改变失稳转速区间的范围,并且主刚度调节在实际工程应用中易于实现,因此可解决实际问题.

图7(d) 表达了交叉刚度 Imag(A-B) 随外阻尼比c的变化规律,由图7(d) 可以看出交叉刚度Imag(A-B) 不随外阻尼比c的改变而改变,但是对比图3(d)、图4(d)和图5(d)可知外阻尼能够很好抑制充液转子的振动,实现转子的增稳.

6 结论

本研究针对有黏性部分充液转子动力稳定性进行了理论研究,结果表明,超重力离心机转子系统在临界转速 ωX之上存在2 个液固耦合激振诱发的失稳区域,并有以下结论.

(1)当系统其他参数选定为初始参数时,流体黏度等级变化范围为ISO VG 22～ISO VG 46,转子系统失稳转速区间为(1.02～1.2) ωX;充液比变化范围为1.67～2.00,转子失稳转速区间为(1.07～1.14) ωX;由主刚度决定的失稳转速区间是变化的;主阻尼系数变化范围为0～5 N·s/m,转子失稳转速区间为(1.01～1.20) ωX,提高转子系统稳定性的关键在于各参数之间实现最优组合,这一结论可为工程中的充液类转子的整体设计提供参数指导.

(2)除主阻尼外各因素均是通过改变充液转子液盘的等效交叉刚度实现转子增稳,因此,在实际工程应用中可采用变参数(如调节充液比、主刚度和主阻尼) 控制技术与控制算法,当保证充液比大于1.82,主刚度为90 MN/m,无量纲阻尼系数大于3.14×10-4时,对充液类转子振动抑制与增稳效果明显.

(3)本研究的计算思路及结论可针对工程中现有的充液类转子的稳定性分析计算,并提供增稳策略.在以下范围内,黏度等级为ISO VG 22～ISO VG 46、充液比为1.67～2.00、主刚度为10～90 MN/m、主阻尼系数0～5 N·s/m,当系统其他参数选定为初始参数时,通过降低液体黏度、增加充液比、增大主刚度以及增大外阻尼均有利于提高充液转子的稳定性.

(4)本研究与其他论文相比采用了数值解的计算方法求解了纳维-斯托克斯方程,避免了解析解带来的极端梯度的现象,并采用状态空间降阶的方法求解了特征值,大幅提高了计算效率,节约了计算时间,在多工况计算时尤为显著.