强迫振动下垂直管道固液两相流数值模拟研究1)

万初一 范祖相 周 岱 韩兆龙 朱宏博 ,2) 包 艳

* (上海交通大学船舶海洋与建筑工程学院,上海 200240)

† (上海齐耀动力技术有限公司,上海 200240)

引言

颗粒的管道输运被广泛应用在深海采矿工程中.海底矿物被粉碎后形成粒径大于1 mm 的粗颗粒,与海水混合后形成粗颗粒固-液两相流,通过管道输运到海面[1].管道中流场特性、颗粒在管道中的分布、速度等与管道的输运效率密切相关.因此,对管道中流场和颗粒的特性展开研究至关重要.对于粗颗粒固液两相管道流的研究已有很多,但大多针对固定管道;由于海洋外流流动的影响,扬矿管道会产生流致振动(fluid-induced vibrations,FIV)现象[2],而针对振动管道中粗颗粒固液两相流的研究相对较少.

在过去的几十年中,很多学者针对静止固液两相流管道中的固液流动特性进行了广泛的试验探究[3-6].Alajbegović等[7]通过使用两种不同种类的圆球形颗粒,研究竖直管道固液两相上升流中的相分布湍流结构,发现在较高的流体流速下,近壁区域几乎没有粒子分布.液体的流速越高,在管道的中心线处颗粒与液体之间的相对速度就越低.液相湍流受粒子密度变化的影响不大.Xia 等[8]通过试验方法,得到了由惯性主导的锰结核和水的混合物通过垂直管道向上流动产生的水力梯度公式.Wijk 等[9]针对管道输送提出了一个稳定性分析理论,并用实验证明了该理论的适用性.Song 等[10]采用不同直径锰结核进行了一系列管道流实验,发现压力损失的演变与固液两相流动状态有关,且受流体速度和颗粒尺寸的显著影响.刘磊[11]采用内径100 mm 的竖直管道进行试验,发现管道颗粒速度、滑移速度主要受到管道局部流速的影响.随着流速的增大,颗粒速度明显增大,滑移速度先增大后减小;随着进料浓度的增大,颗粒速度略有增大,滑移速度略有减小.然而,实验方法对颗粒间的相互碰撞、湍流-颗粒间的作用等相对难以观测,因此诸多学者采用数值模拟方法对固液两相流进行深入研究.

随着计算技术的发展,数值模拟已成为预测管道中多相流动特征的有效工具.相比适用于细颗粒的欧拉-欧拉法[12],欧拉-拉格朗日法[13]可以模拟单个颗粒的运动,并较容易地考虑颗粒间与颗粒-壁面碰撞,更适合粗颗粒的模拟[14-15].对于流体中粗颗粒运动特性的研究,Tsuji 等[16-17]提出了结合计算流体动力学(computational fluid dynamics,CFD)和拉格朗日框架下的离散元[18](discrete element model,DEM)的CFD-DEM 方法.此方法随后被很多学者采用,描述颗粒-流体的运动[19-21].Zhou 等[13]通过CFD-DEM 模拟,发现增加进料浓度增加了时均固体体积分数,同时降低了管道中心区域的时间平均轴向液体速度和轴向固体速度.提高输送速度会在管道中心区域降低时间平均固体体积分数.增加粒径会降低管道中心区域的时间平均固体体积分数,但对压降的影响不大.Dai 等[22]发现较大的颗粒浓度会促进堵塞的发生,影响管道的流动稳定性,增加壁面剪应力.提高内部流速可以促进流畅的流动,但会增加壁面剪应力.随着粒径的增大,颗粒的提升速度逐渐减小,对流体的追随性降低.Teng 等[23]发现随着初始固体体积分数的增加,液体和固体速度减小,但总压降增大;初始混合速度的增加增大了总压降.综上,静止管道中固液两相流的研究已有很多,但对于静止管道内流的分析方法以及所得结论不一定适用于振动管道[24].

针对振动管道的内部流场的研究,Xia 等[24]发现振动垂直管的水力梯度大于固定管.与固定管道相比,振动管道中颗粒与壁面的碰撞更频繁,导致更高的动能损失,进而导致更高的压降.Zhang 等[25]发现壁面摩擦力对振动垂直管中颗粒的上升有显著影响.刘勇等[26]采用双欧拉方法,研究了涡激振动对深海采矿矿物颗粒水力提升的影响,发现管道的涡激振动会改变颗粒轴向速度分布和颗粒浓度分布.徐海良等[27]采用双欧拉方法,对横向摆动工况下的扬矿管内固液两相流进行模拟仿真,发现除管壁附近外,摆动工况下颗粒轴向速度沿管径基本呈线性分布,摆幅越大,轴向速度径向分布梯度越大,径向不对称性越严重.综上所述,对于振动状态下的管道内部多相流的研究不多,尤其是对适用于深海采矿工程的管道中粗颗粒固液两相流的研究更少.

因此,本文采用适用于粗颗粒数值模拟的欧拉-拉格朗日方法,针对振动管道对流场的变化和颗粒的动力学特性的影响展开研究.为简化计算和便于分析,本文将柔性管道设定为刚体管道,并只对管道进行单一方向(X向)的受迫振动.

1 计算方法

1.1 控制方程

流体的控制方程是在N-S 方程的基础上,在方程中引入由于颗粒存在而对流体产生的扰动项,具体方程如下

式中,εf为流体体积分数.

式中,Vi,part为颗粒总体积,Vcell为网格体积,n是与网格体积重叠的颗粒数,ρf为流体密度,uf为流体速度,pf为流体压力,g为重力加速度,Rf为应力张量,fsf为从颗粒到流体的体积相互作用力.在DEM模型中,考虑了颗粒的平移和旋转运动,包括动量方程和角动量方程

式中,mp为颗粒质量,up为颗粒速度,ffs表示从流体到颗粒的体积相互作用力

式中,fd为曳力,fl为升力,fp为压力梯度力,fam为附加质量力.fc表示颗粒间的接触力.Ip与 ωp分别为颗粒的惯性矩和角速度,Mct是颗粒受到所有其他颗粒的接触力矩,Mfs是颗粒受到流体的力矩.

同时,利用离散随机游走(discrete random walk,DRW)模型模拟了湍流对颗粒的影响,该模型假设颗粒在湍流场时经过特定时间和长度尺度的湍流涡序列[20].这些涡旋代表了雷诺平均速度场的局部扰动.在DRW 模型中,瞬时流体速度被分为平均速度和随机产生的波动速度,对粒子施加作用力.波动速度值服从正态高斯分布.

1.2 CFD-DEM 耦合方法

本文采用CFD 方法对流体域进行建模,其中定义了管道的几何条件和边界条件.另一方面,DEM用于定义颗粒并指定它们的物理属性,包括尺寸、形状和材料属性等.这两种方法通过在流体和颗粒之间交换动量、能量和质量实现耦合.这种相互作用通过使用子时间步长方法实现,其中流体和颗粒分别被求解,并且在每个子时间步长进行两种方法之间的信息交换.最后,将耦合的CFD-DEM 方程进行迭代求解,直到颗粒流的整体系统达到稳态或期望值.

1.3 计算时间步长设置

液相模拟采用了可实现的k-ε湍流模型.颗粒时间步长受瑞利时间步长 ∆tp的限制[28-29],其表达式为

式中,µp与Ep分别为颗粒的泊松比和杨氏模量.

经过对 ∆tp计算并考虑了计算成本,本文取颗粒时间步长为10-5s;同时,将流体的时间步长设定为10-4s[30].

2 模型描述与验证

2.1 边界条件设置

管道高度H为2.5 m,直径D为0.0306 m.在管道两端分别设置速度入口和压力出口的边界条件,管道壁面处采用无滑移边界条件.振动管道的运动位移方程和管道振动速度方程分别为

式中,A为管道的振幅,f为振动频率,v为管道的振动速度.在本文中,振幅取2 倍和5 倍的管道直径,即0.0612 m 和0.153 m;振动频率取值为1 Hz 和1.5 Hz.采用结构化网格建模,一共150199 个网格和158000 个节点.管道模型如图1 所示,更详细的参数设置,参见文献[30].

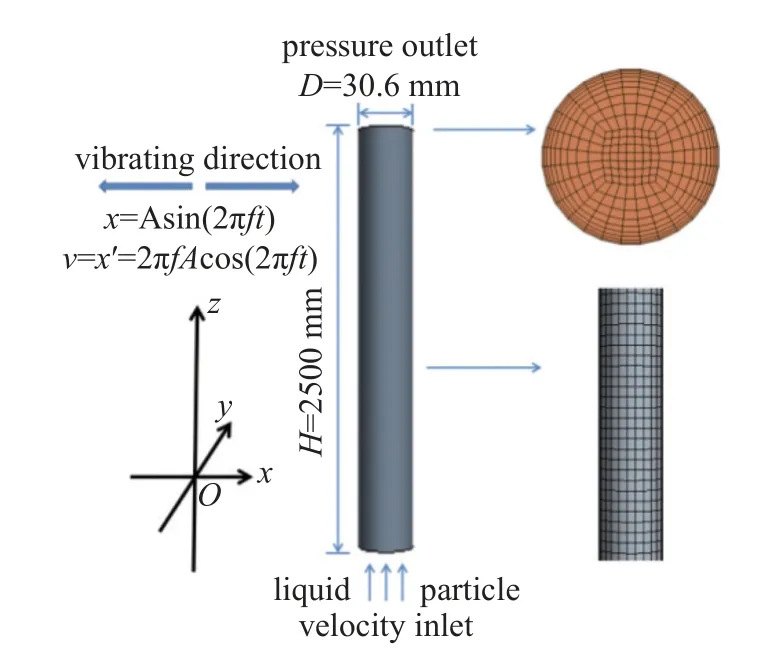
图1 管道建模Fig.1 Pipe modeling

2.2 初始设置与材料参数

颗粒为球形,直径分别为1.64 mm,2.32 mm和3 mm,分别称为小颗粒、中颗粒和大颗粒.初始混合固液两相流的输送速度为2 m/s,进料体积浓度为5%.流体的密度与动力黏度分别为998 kg/m3和0.001 Pa·s,颗粒的杨氏模量、泊松比和密度分别为1.0×107Pa,0.3 和2450 kg/m3.颗粒彼此间碰撞恢复系数和颗粒与壁面间的碰撞恢复系数分别为0.85 和0.95;颗粒间的滑动摩擦系数和静摩擦系数分别为0.01 和0.1;颗粒与壁面间的滑动摩擦系数和静摩擦系数分别为0.01 和0.1.

2.3 模型验证与独立性研究

在模拟开始前,首先要进行模型的验证与相关独立性的研究.本文选取Alajbegović等[7]的实验结果进行验证.两相流从管道底部均匀注入,流体流速分别为1.888 m/s 和2.196 m/s,固体流速分别为0.045 m/s 和0.060 m/s,总质量流速分别为1.469 kg/s 和1.723 kg/s.同时,为了保证数值结果的可靠性,在模拟之前研究了可能影响模拟的各种因素,包括网格分辨率、计算时间和管道高度的独立性.考虑了5 种网格尺寸,分别对应于网格数220059,178143,150199,102295 和72355,分别称为超细网格、细网格、中等网格、粗网格和超粗网格.分别对2 s,3 s,4 s 和5 s 的不同计算时间进行了模拟,所取数据所在位置分别在2.1 m,2.2 m,2.3 m 和2.4 m 不同高度的横截面.权衡了计算精度与计算时间后,本文选择中等尺寸网格、取计算4 s 后的模拟时间、高度为2.4 m 的横截面、位于管道高度2.1～2.4 m 之间的流型以及颗粒数据进行后续模拟[30].相比于之前的工作,本文的不同之处在于:选取了单一粒径的粗颗粒而非级配粗颗粒,管道也处于振动状态而非静止.

图2 为模型验证计算过程中管道内固液两相流的径向和轴向截面[30],如图2(a)～图2(d)所示,颗粒体积分布趋势和轴向流体速度趋势与原实验结果和他人的模拟结果吻合较好[7,13,20].图2(e)为粗颗粒固液两相管道流轴向剖面图.

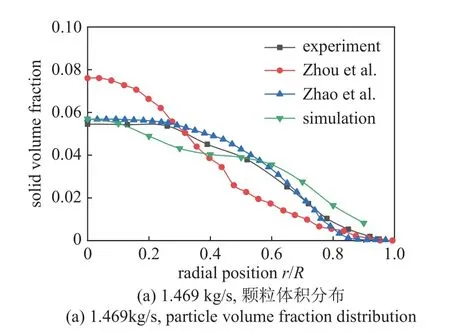
图2 模型验证[30]Fig.2 Model validation[30]

3 粒径对流动特性的影响

本节针对振动管道的不同颗粒展开分析,颗粒直径分别取1.64 mm,2.32 mm 和3 mm.内流速度为2 m/s,进料浓度为5%.图3 显示了颗粒在不同时刻的瞬时位置和速度.在图中,T表示一个周期,N表示完全振动周期次数.每幅图都根据上方绘制的正弦函数进行标记,并从左到右排列,以描述一个完整的振动周期的初始时刻、1/4 周期时刻、1/2 周期时刻和3/4 周期时刻,分别用时刻一、时刻二、时刻三和时刻四表示.同时,这4 个时刻也与图4 的4 幅图相对应,图4(a)～4(d)分别对应时刻1、时刻2、时刻3 和时刻4.时刻1 表示管道有向X轴正方向位移的趋势,位移为0,速度最大;时刻2 表示管道已经达到了X轴正向位移最大位置,此时速度为0;时刻3 表示管道在X轴正向最大位移处转头向X轴负方向运动了2 倍管径,此时位移依旧为0,但速度最大,朝向X轴负向;时刻4 表示管道在X轴负向位移最大,但速度为0.

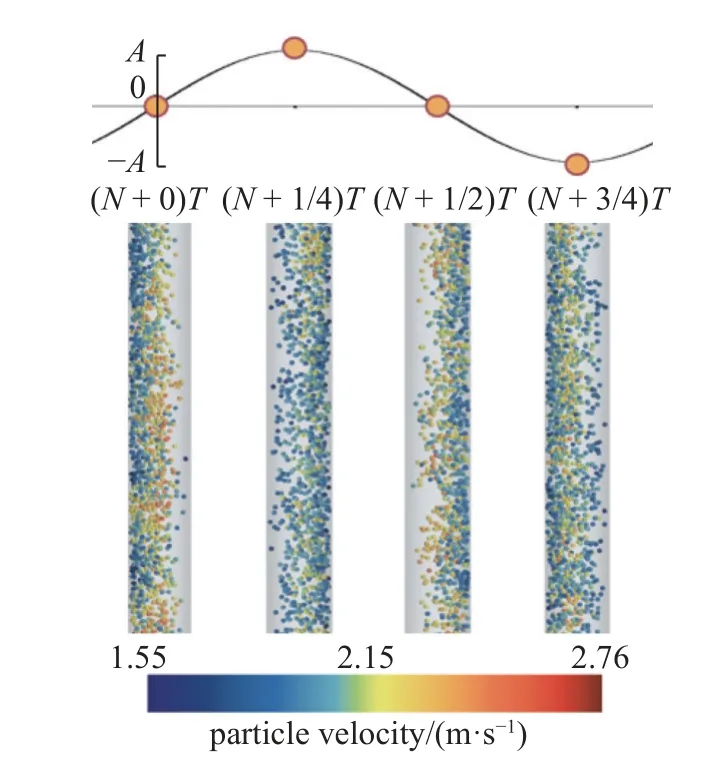
图3 不同时刻颗粒分布Fig.3 Particle distribution at different times

图4 瞬时颗粒速度与位置分布Fig.4 Instantaneous particle velocity and position distribution

3.1 粒径对颗粒动力学特性的影响

图4 为颗粒瞬时速度与位置分布,每张图的从左到右,分别代表小颗粒工况、中颗粒工况和大颗粒工况.而图4(a)～图4(d)分别代表3 种工况的不同瞬时时刻,分别代表时刻1～时刻4,均选取自管道流场稳定后的数据.图4(a)代表的瞬时时刻对应管道位移为0、速度最大时.可以看到此时颗粒几乎都聚集在了管壁附近,粒径越小,此现象越明显.此图与图4(d)联动分析:图4(d)的小颗粒工况为管道位移最大、但速度为0 时刻的颗粒瞬时速度与分布.在此时刻,小颗粒整体上偏向左侧,但聚集程度不如图4(a)表示的时刻1.这是因为颗粒存在惯性,管道的运动状态与颗粒并不同步,需要一定时间后颗粒才会分开流体,抵达左侧管壁.而图4(a)在时间上为图4(d)的拓展.可以看到经过了1/4 个周期的时间,管道向右位移了2 倍直径的距离,速度向右;而图4(d)中,颗粒的运动惯性为向左运动.这样造成了两者的冲突,导致在图4(a)中,颗粒大量地聚集在了左侧管壁.而中颗粒和大颗粒工况相比于小颗粒工况,趋势不明显,是因为两者的惯性相对较大.在图4(d)中,颗粒均有朝着管道左侧壁面运动的趋势,但大颗粒的惯性相对小颗粒更大,它们受到流体、管壁推动时,相对不容易改变自身的运动趋势.由研究可知[13,30],颗粒在竖直管道中输运,相对集中在管道中心附近.因此大颗粒的惯性令其保持相对聚集管道中心、不被管道和流体来回推动的运动状态.

图4(b)为紧接着图4(a)的下一时刻,表示管道向X轴正向运动1/4 周期后的瞬时颗粒状态.此时管道运动到了X轴正向最大位移处,速度逐渐降低为0.可以看到颗粒从图4(a)中的相对紧贴左侧管壁,变为了更偏向管道右侧,分布情况与相差半个周期的图4(d)类似.同样地,这是因为颗粒具有惯性,在管道减速的同时,颗粒依靠自身惯性,反而更向管道右侧移动.这就导致虽然管道此瞬时的速度为0,但颗粒依旧从管道左侧运动到了偏向管道右侧的位置.图4(c)的工况为图4(a)工况继续运行1/2 个周期后的瞬时颗粒状态,两者工况相似,结论相似,因此本文不再赘述.

同时,在所有工况图中,与管壁接触的区域的颗粒速度出现了明显下降.这是因为颗粒与管壁接触,两者发生了摩擦、碰撞,导致颗粒的动能损失.这也导致了流体需要更大的能量将颗粒输运到管道上端,极大地影响了管道压降.

图5 为颗粒的轴向速度与滑移速度.由图可知,随着粒径增大,颗粒的轴向速度与滑移速度均逐渐增大.这是因为大颗粒相对更加不容易被流体推动,因此流场增大速度以提升曳力,导致轴向流场速度和轴向颗粒速度的增加.滑移速度为颗粒跟随流体能力的量度,滑移速度越大,流体施加在颗粒上的曳力越大[30].滑移速度也随着粒径增大而增大,是因为颗粒的质量增大,流体需要更大的能量来推动颗粒,对其施加的曳力也要相应增大.而曳力的大小又与滑移速度相关.因此想要提升大颗粒,滑移速度也要相应增大.

图5 轴向颗粒速度与滑移速度Fig.5 Axial particle velocity and slip velocity

3.2 粒径对颗粒体积分布的影响

图6 与图7 为时均颗粒体积分布图与管道截面上的径向时均颗粒体积分布图.图7 中,横坐标范围为0～1.0 表示管道中心处,1 表示管道壁面处.可以看到,相比于尺寸较小的中颗粒和小颗粒,大颗粒更倾向于聚集在管道壁面附近,而小颗粒更倾向于聚集在管道中央.这是因为相比于小颗粒,大颗粒的惯性更大.在管道作周期性横向振动时,管道对流体施加了力,令流体水平方向运动;流体随之对颗粒施加水平方向的升力.在流体对颗粒施加水平向的升力时,惯性较小的小颗粒会被推动,移动向管道中心;而惯性较大的大颗粒更倾向于停留在原处,不容易改变自身运动状态.由之前的工作可知,颗粒在静止、竖直管道中运行时倾向于聚集在管道中央处[13].而在管道横向振动时,管道原有的位置坐标改变,因此原来停留在管道中央处的大颗粒,在较大惯性下,表现为聚集在管道壁面附近.

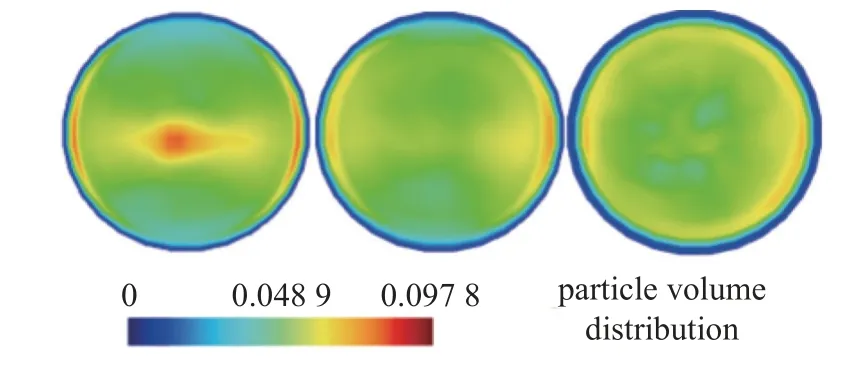
图6 时均截面颗粒体积分布Fig.6 Time-averaged particle volume distribution on the cross-section

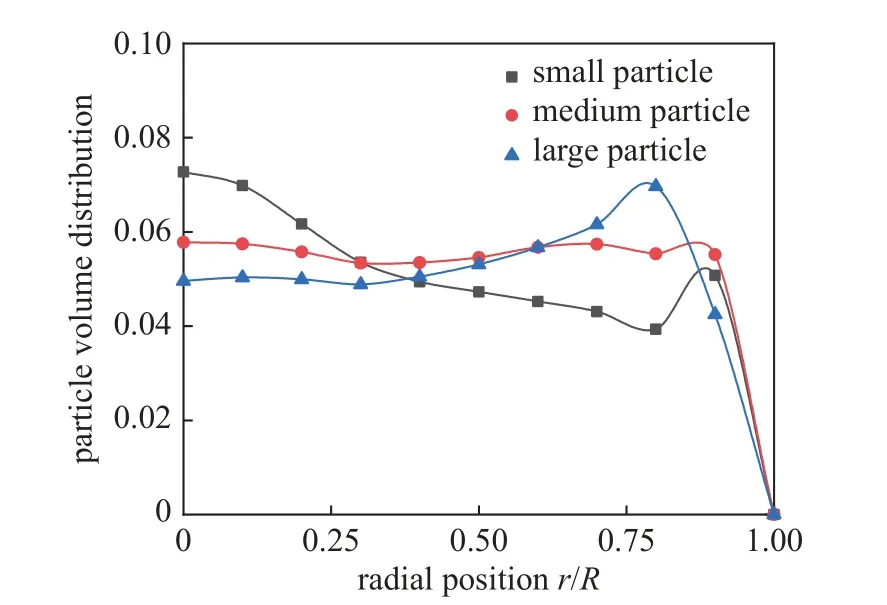
图7 径向方向的时均颗粒体积分数Fig.7 Time-averaged particle volume fraction in the radial direction

3.3 粒径对流场的影响

图8 为时均轴向流场速度,其中图8(a) 与图8(b)分别为时均截面流场速度分布与时均截面轴向流场速度平均值.由图可知,随着粒径增大,轴向流场速度也随之增大.如前所述,为了将颗粒输运到管道上部,流场需要向颗粒提供曳力作用.而颗粒粒径越大,质量越大,所需的曳力也相应增大.因此,流体的轴向速度增加.

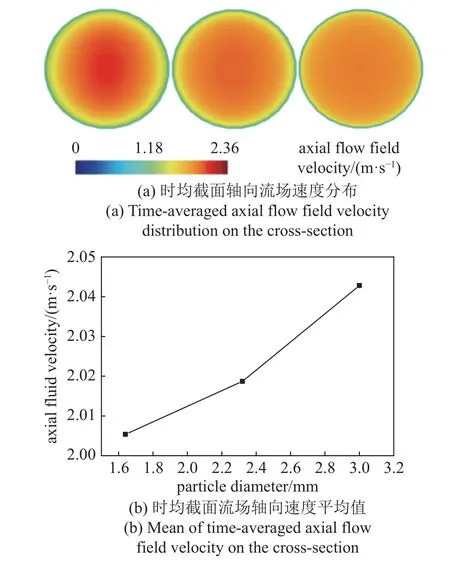
图8 时均轴向流场速度Fig.8 Time-averaged axial flow field velocity

图9 为时均流场湍动能与湍流耗散率,其中图9(a)与图9(b)分别为时均截面流场湍动能分布与时均截面流场湍动能与湍流耗散率平均值.可以看到时均湍动能与湍流耗散率的截面平均值均随着粒径增大而增大.这是因为大颗粒惯性较大,随管道、流体运动而横向位移的幅度较小,这与流体的运动趋势不一致,颗粒对流场的扰动较大;湍流耗散率表示流体动能转化为内能的量度,颗粒越大,对流场扰动越大,颗粒与流体间互相摩擦所损耗的动能也相应增大.这也导致了流场需要更大的能量输送颗粒,对应下节中对压降的分析.

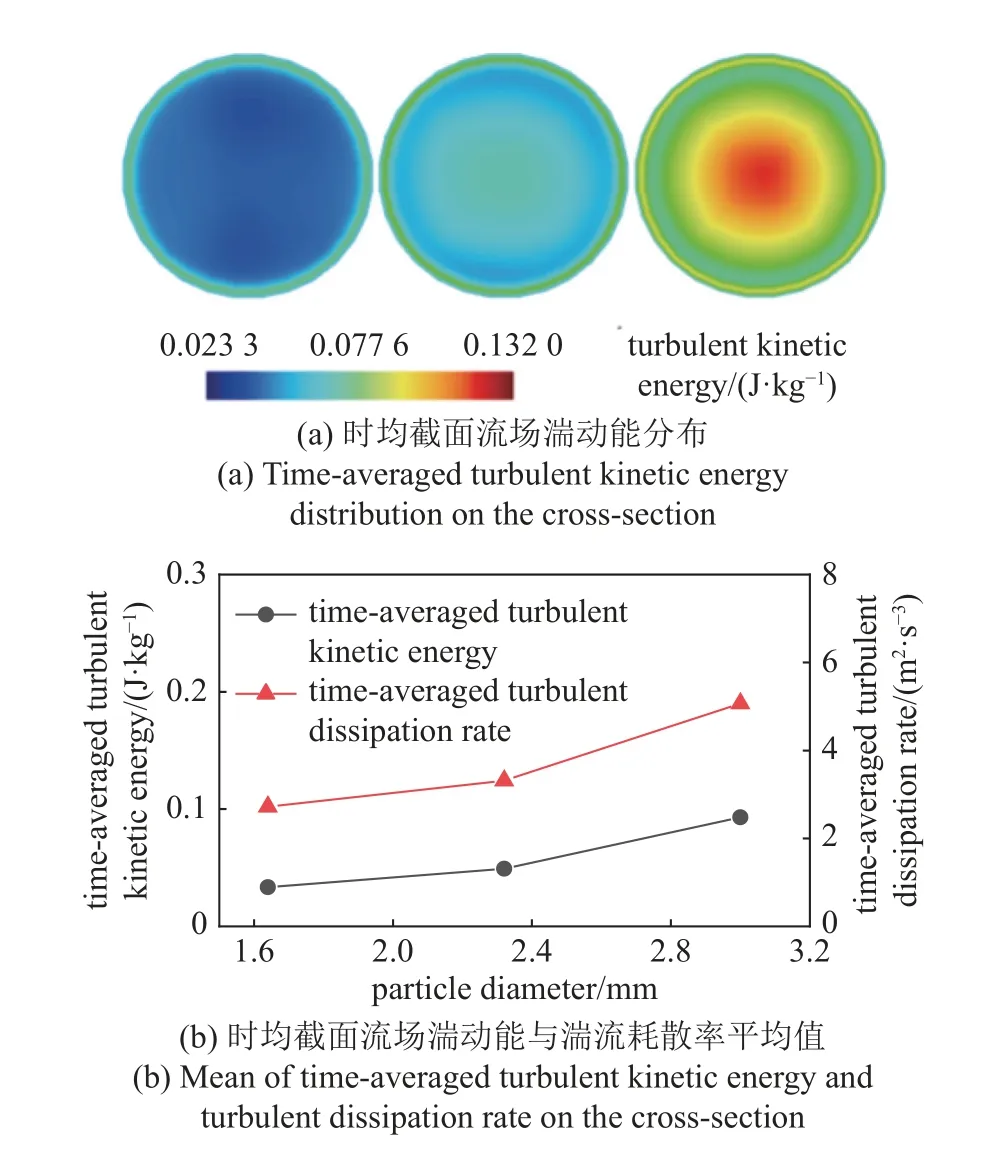
图9 时均流场湍动能与湍流耗散率Fig.9 Time-averaged turbulent kinetic energy and turbulent dissipation rate of the flow field

3.4 粒径对管道压降的影响

图10 所示为管道振动速度最大时刻的瞬时壁面剪应力的值.从左到右,分别对应小颗粒、中颗粒和大颗粒工况.与图4 相同,图10(a)～图10(d)分别代表3 种工况的不同瞬时时刻,均选取自管道流场稳定后的数据.对于图10(a)中的小颗粒工况,可以看到管道左侧的壁面剪应力相对右侧较小,而此瞬时时刻与图4(a)的小颗粒工况的颗粒分布相对应.在颗粒分布少的区域,壁面剪应力更大,这说明流场影响所形成的剪应力大于颗粒的影响.而颗粒在管壁附近的存在对流场形成了干扰,存在颗粒数量越多,这种干扰令剪应力减少得越多,因此表现为在图10(a)中,管壁左侧剪应力较小,而右侧较大.对于图10(b),由于此时刻为速度为0、位移最大,颗粒在管道中的分布更偏向于分散在管道中而不是贴在一侧管壁上,因此颗粒对管道左右两侧流场的扰动相差不大,两侧管壁的剪应力相差较小.

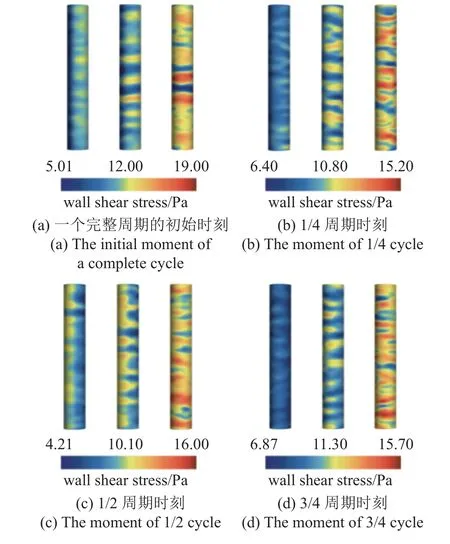
图10 管道瞬时壁面剪应力Fig.10 Instantaneous wall shear stress of the pipe

由图4 的分析可知,相比于小颗粒,大颗粒惯性较大,无论哪个时刻,大颗粒在管道中的分布都较分散,因此在图10 的4 个时刻,管道壁面剪应力分布均很相似,与小颗粒工况的壁面剪应力工况存在很大不同.无论哪一个瞬时时刻,小颗粒工况对应的壁面剪应力值均相对最小,而大颗粒工况的壁面剪应力值最大.这是因为小颗粒相比于大颗粒,数量更多,这样即使在壁面附近的颗粒浓度较小,但依旧能存在足够数量的颗粒来扰动流场.图10(c)与图10(d)的工况与图10(a)和图10(b)相似,机理相似,不再赘述.

图11 为管道壁面剪应力与管道无量纲压降时均值,两者均选取管道高度为2.1～2.4 m 间的流场与壁面,经过4 个完整振动周期后的平均值.可以看到,壁面剪应力与管道无量纲压降均随着粒径的增加而增大.由前文第3.1 小节的分析可知,大颗粒更倾向于聚集在壁面附近,而小颗粒则是随着管道振动,被流体推动到管道中央.因此,壁面附近受到的大颗粒的摩擦、碰撞较为频繁,剪应力相对更大.管道的无量纲压降定义为

图11 管道壁面剪应力与无量纲压降Fig.11 Wall shear stress of the pipe and dimensionless pressure drop

式中,∆p为两截面间的压力差,ρf为流体密度,∆h为两截面间的高度差.可以看到,管道的压降随着粒径的增大而增大,这与Li 等[31]的研究结论相一致.这是因为大颗粒间彼此碰撞、与流体间相互作用导致的动能损失较大,因此流体需要更多的能量输运颗粒[13].而且随着粒径增大,颗粒更加倾向于聚集在壁面附近,与壁面摩擦应力增大,也增加了动能的损耗.因此,管道压降增加.

4 振幅与振动频率对流动特性的影响

本节针对振动管道的不同振幅与振动频率展开分析,颗粒直径为2.32 mm,内流速度为2 m/s,进料浓度为5%.图12～图14 从左到右的工况分别为振幅2D,频率1.5 Hz;振幅2D,频率1 Hz;和振幅5D,频率1 Hz.在本节中,3 个工况分别用高频率工况、标准工况和高振幅工况表示.其中标准工况即为第3 节中的中颗粒工况.

图12 为管道截面上的径向时均颗粒体积分布图.可以看到相比标准工况,高频率工况与高振幅工况的颗粒分布明显更偏向于聚集在管道壁面,这与前文对图4 的分析类似:高频率工况下,流体被管壁更加频繁地改变方向左右推动,进而推动颗粒横向移动;而颗粒由于惯性,倾向于停留在原处,不容易改变自身运动状态.管道高频率振动下,颗粒对流体的横向跟随性较差,因此表现为聚集在管壁.对于高振幅工况,颗粒由于惯性停留在管道中部,在管道振动状态下被管壁与流体推动而横向运动.而当振幅更大时,颗粒被管壁推动,与管壁的距离更紧密,表现为相对更加聚集在壁面附近.

图13 为管道截面上的时均轴向流场速度分布图.可以看到随着管道振动的频率和振幅变化,轴向流场速度变化较小.在第3 节的分析中,大颗粒由于本身的更大惯性,导致流场需要更大的速度进行输运.而本节的3 种工况,颗粒尺寸相同,因此流场输运颗粒所需动能也相差不大.

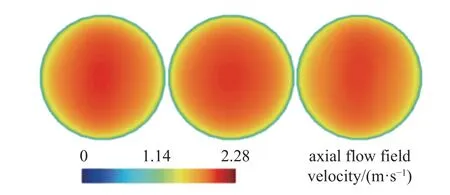
图13 时均截面轴向流场速度分布Fig.13 Time-averaged axial flow field velocity distribution on the cross-section

图14 为时均截面流场湍动能分布.可以看到相比标准工况,高频率和高振幅的两种工况的湍动能相对更大.这是因为此两种工况下,颗粒时均分布相对更贴近壁面,由于运动的相对性,相当于颗粒在管道中的横向运动更频繁、幅度更大,因此对流场的扰动更大.

图14 时均截面流场湍动能分布Fig.14 Time-averaged turbulent kinetic energy distribution on the cross-section

5 进料浓度对流动特性的影响

本节针对振动管道中不同进料浓度展开分析,颗粒直径为2.32 mm,内流速度为2 m/s,进料浓度分别为2.5%,5% 和7.5%.振幅为2D,振动频率为1 Hz.图15～图17 从左到右的工况分别为浓度2.5%、浓度5%和浓度7.5%.在本节中,3 个工况分别用低浓度工况、标准工况和高浓度工况表示.其中标准工况即为第3 节中的中颗粒工况.

图15 时间平均颗粒体积分布Fig.15 Time-averaged particle volume distribution on the cross-section

图15 为管道截面上的径向时均颗粒体积分布图.可以看到在3 种工况下,随着颗粒浓度增大,颗粒分布逐渐从更聚集在管道壁面,过渡到在管道中心和壁面处都有大量聚集.对于颗粒聚集在壁面的现象前文已有分析;对于高浓度工况出现的部分颗粒聚集在管道中心的现象,是因为随着浓度增大,颗粒对流场的扰动也更加剧烈,改变了颗粒两侧的流体流速,也令颗粒所受的升力发生改变.改变后的升力更容易将颗粒从壁面推向管道中心;同时,大量的颗粒彼此碰撞,发生剧烈的动量交换[30],也会使部分颗粒从壁面附近被碰撞到管道中心位置.

图16 为管道截面上的时均轴向流场速度分布图.可以看到随着进料浓度的增大,轴向流场速度逐渐增大.这是因为随着浓度增大,颗粒需要更大的曳力提升,同时颗粒间彼此碰撞也损耗大量动能,因此流体的速度也需相应增大以提升曳力.

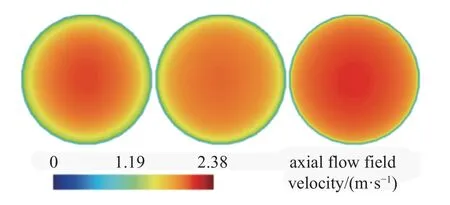
图16 时均截面轴向流场速度分布Fig.16 Time-averaged axial flow field velocity distribution on the cross-section

图17 为时均截面流场湍动能分布.可以看到随着进料浓度的增大,流场湍动能逐渐增大.这是因为颗粒数量增多,颗粒彼此碰撞、颗粒与流体间的作用更加频繁,对流场的扰动也相应增大,这也与前文对图15 的分析相似.

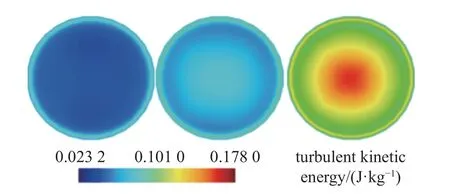
图17 时均截面流场湍动能分布Fig.17 Time-averaged turbulent kinetic energy distribution on the cross-section

6 结论

本文通过CFD-DEM 方法,对竖直管道在强迫振动作用下不同粒径、不同振幅和振动频率以及不同进料浓度的固液两相流的特性展开研究,得到主要结论如下.

(1)相比大颗粒,小颗粒惯性较小,更容易被流体所推动,流体在推动颗粒的过程中消耗了动能,流体速度较小.同时,颗粒横向位移扰动了流场,颗粒与流体发生摩擦损失了动能并转化为内能.粒径越大,颗粒惯性越大,导致流场时均湍动能与湍流耗散率越大.大颗粒的惯性更大,在管道振动时不容易被管壁、流体推动,因此相比于小颗粒,大颗粒更倾向于聚集在管道壁面附近.颗粒间以及颗粒与壁面间的摩擦、碰撞更加频繁,因此需要更多能量输运,压降相对更大.

(2)增大管道振动频率与振幅,对轴向流体速度的影响较小,但均会导致湍动能的增加,是因为在此过程中颗粒对流场的扰动显著增大,而并未损失较多的动能.颗粒的分布更趋向于聚集在壁面,是因为管道高频率和高振幅振动下,颗粒对流体的横向跟随性相对较差,表现为贴在壁面附近.

(3)进料浓度从小到大变化,流场轴向速度和湍动能都变大,是因为较大的颗粒浓度扰动流场.颗粒的分布从大量聚集在管壁到中心位置也有聚集,因为受到扰动的流场形成更大升力,并且颗粒间的动量交换也更加频繁和剧烈,推动颗粒向管道中心位置移动.