闪烁的神经网络

陈凯

摘要：本文给出了一种基于数字逻辑电路的模拟神经元行为以及构建简单神经网络的方法，主要围绕非线性的异或运算的实现，完整呈现了基于随机发生器、计数器、数字比较器和逻辑门等数字逻辑元件模拟神经元行为和构建神经网络的过程，并讨论了其在基础教育领域人工智能教学中的可能用途。

关键词：感知机；神经网络；异或门；数字逻辑电路

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2024）07-0023-05

“罗森布拉特认为，人的智能行为以人类对世界的整体了解为基础，很多智能行为很难被形式化。在20世纪50年代，罗森布拉特提出了一种新的实现智能行为的思路，即构建一种能够自动学习并恰当辨别模式、作出响应的神经网络，他首次引入了感知机的概念，这是一种模拟人脑感知和学习能力的模型，可以对感知机进行训练，使之能实现特定的分类识别功能。不过，明斯基对感知机的看法则相对悲观，他认为感知机作为线性模型，无法表示非线性的函数，即便是简单的如异或（XOR）逻辑运算也难以实现。1969年，明斯基和西摩·佩珀特写作出版了《感知机》一书，用数学证明感知机的局限性，他们的观点对神经网络的研究造成了严重的打击，使得神经网络研究陷入了长达10年的低潮期。”

以上文字主要由某人工智能语言工具生成，笔者略微做了一些整理。罗森布拉特和明斯基都是人工智能研究界巨擘，两人围绕感知机的争论俨然成为一桩公案。从今天所知回顧历史，便知罗森布拉特和明斯基都受制于历史局限，现在的人们知道，具有多层感知机的神经网络可以表示用单层的感知机无法表示的非线性函数。在基础教育阶段，学生在学习神经网络时，可能会因为无法直观地看到模拟神经元的工作过程，而对整体神经网络的原理缺乏真切的理解，也就难以体验到多层感知机在解决表示非线性函数这个问题上的思维方法的突破。正因为这样，笔者希望能找到具有如下特性的工具：用某种模型实现神经元和突触行为的底层的模拟，提供将虚拟神经元搭建成神经网络并展现运行过程与效果的平台，神经元的生成和连接方便，神经网络的架构过程最好能通过在图形化的环境中拖拽图标来完成，且有一定的可定制性；能使用可视化工具将神经网络的结构和工作过程显现出来，并提供一定的神经网络架构、训练参数、训练指标的设定的人机交互接口；获取和安装方便，软件是开放的，没有版权上的限制，较少依赖特殊的工作环境。

然而，能满足以上要求的现成工具却很难找到，这就促使笔者思考，如何“亲手打造”这样一种神经网络实验环境。本文要介绍的项目名为“闪烁的神经网络”，在这个神经网络中，虚拟神经元对来自输入信号的总体的闪烁的频率进行计数，当计数达到阈值时，该虚拟神经元也开始以闪烁来对外发送信号，其行为如图1所示。

之所以通过闪烁频率计数来判定阈值，是因为能够在教学演示中展现出直观形象的动态效果：闪烁的频率能体现出神经元的运动状态，而且因为对闪烁的计数需要一定的时间，信号的传递过程和神经元的变化过程能被头脑注意并观察到，神经网络工作的内部因果关系也就清晰地呈现出来了。

将这样的多个行为简单的神经元连接组合到一起，就可以涌现出复杂的行为。而用来制作神经元和神经网络的工具，则出乎意料地使用了数字逻辑模拟器（数字逻辑仿真软件）。对已有文献的考察可知，很少有人将数字逻辑模拟器用于神经网络的搭建和运用，其中可能有多方面的原因，如数字逻辑模拟器较难实现浮点数的运算、无法批量生成神经元和快速搭建神经网络（这里不考虑采用硬件描述语言生成神经网络的情况，类似的神经网络实现方法所需要的知识技能超出基础教育阶段绝大部分学习者的水平）、很难用数字电路本身来进行基于机器学习的调参（稍微复杂一些的基于数字电路的神经网络，其中的诸多工作参数仍然需要计算机环境下的神经网络算法来计算获得）。所以，数字逻辑模拟器并不是一种值得推荐的作为生产工具的神经网络架设环境。但对于人工智能的初学者来说，数字逻辑模拟器提供了一个图形化的实验环境，除了刚才提到的神经网络的运行过程能直观显现出来之外，神经网络从构想到架设再到运行验证，都能由学习者亲手操作把控。本文使用Logisim数字逻辑模拟器来构造神经网络，其中的电路当然也能迁移到其他功能完备的数字逻辑模器中，甚至可以采用真实的元件替代虚拟元件来实现神经网络电路。实际上，使用图形化的编程工具也能实现与“闪烁的神经网络”类似的效果，但数字逻辑模拟器提供了一个纯粹硬件的构造平台，更能凸显出基于底层物理现实的“造物”特性。

数字逻辑的神经网络基本组件

组成神经网络的几个基本组件是信号发生器、信号比较器、信号触发器、信号累加器、信号削减器和信号显示器。这些部件的基础元件是随机数发生器、计数器、数字比较器和逻辑门等。

1.信号发生器

最简单的信号发生器是由一个随机数发生器和一个计数器组成的，计数器每次在计满之后，都会产生一个溢出信号1，然后在重新开始计数后溢出信号又变为0，相当于在每次计数计满时发出一个闪烁信号。由于随机数发生器的作用，计数器发出溢出信号的时间是不规律的，这样就能产生出持续重复但又不太规律的闪烁信号。计数器的位数决定了闪烁的总体频率，如3位计数器要计满8个数后才闪烁，4位计数器则要计满16个数后才闪烁。

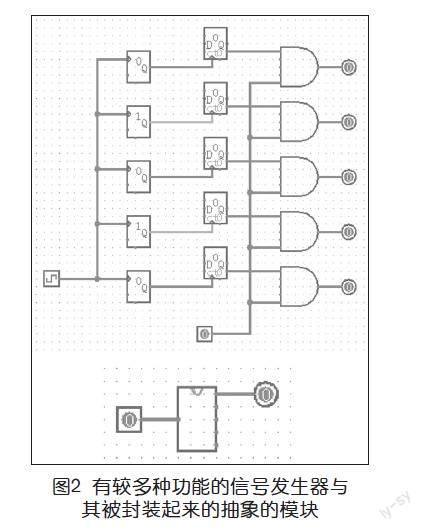
可以为信号发生器增加一些元件，使它能产生出更多效果，如：增加一个输入，通过与门来控制信号发生器是否发生信号，这样就能切换信号发生器的闪烁和静默两种状态；为随机数发生器设定不同的随机种子，加强随机效果；用多套随机数发生器和计数器，来产生不同频率的信号，这样就能设定神经网络中信号的权重。为了便于后续神经网络的搭建，可以将电路封装起来，形成抽象的模块。信号发生器的电路与封装后的模块如上页图2所示。后面将要提到的几个电路也都可以封装成抽象的模块，这里就不一一赘述了。在教学中，可以直接提供封装好的模块，降低学习的难度，同时将模块内部的工作原理作为拓展的学习内容，丰富教学内容的难度层次。

2.信号比较器

信号比较器用来判断在一段时间内，闪烁的计数是否超过阈值。信号比较器由两个计数器和一个数字比较器组成，左面的计数器在计满数后向右面的计数器发送一个清零信号，所以，当输入的闪烁信号频率足够高时，数字比较器就能判别出闪烁频率是否高于一定的阈值，图3是信号比较器的组成电路，其中所示的阈值是6，这个阈值是神经网络中可以通过人机交互进行调整的一个重要参数。

3.信号显示器

信号显示器的结构其实和信号比较器很相近，只是将数字比较器换成一个输出信号的显示，这样能在实验中，观察在一定时间周期里闪烁的次数，电路如图4所示。显示器仅用于调试，在最终运行的神经网络中不是必需的。

4.信号触发器

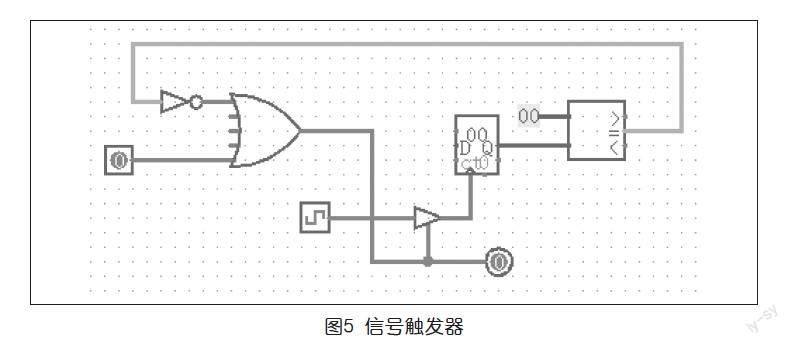
信号触发器模拟了神经元的运行工作过程，只有当输入信号闪烁的频率达到阈值时，神经元才被触发向外发送闪烁信号，它是由计数器、非门、或门、驱动器共同组成的，电路如图5所示。信号触发器的结构稍微复杂一些，不过只要运行起来，它的作用就是显而易见的：当输入信号（来自信号比较器）为1时，计数器就开始计数，在计数过程中，时钟信号能够顺利通过驱动器传输到计数器。当计数器计满后，如果输入信号仍然是1，则继续下一轮计数，如果输入信号是0，则驱动器关闭，时钟信号被阻止传输到计数器，于是停止计数。

5.信号累加器

信号累加器可以是一个简单的或门，也可以是几个或门的组合，如图6所示，它能将几组信号的闪烁合并成一组信号的闪烁。如果神经网络比较简单，就可以直接用或门充当信号累加器，如果神经网络比较复杂，如需要对很多个信号进行或运算，则仍然有必要将其封装成模块。

6.信号削减器

信号削减器由一个非门和一个与门组成，当下端的输入不闪烁时，上端的闪烁信号就能顺利通过与门，当下端输入闪烁时，就会削减掉上端的闪烁信号。电路如下页图7所示。

神经网络实现异或门运算

这里有必要简单说明一下基于多层感知机的神经网络实现异或逻辑运算的原理（实现与、或、非逻辑运算的感知机结构比较简单，有兴趣的读者可自行查阅相关资料）。这个实现异或逻辑运算神经网络由如图8所示的两个输入神经元（最左列）、两个隐藏层神经元（中间列）、一个输出神经元（最右列）组成。在图8中，深色箭头代表信号累加，浅色箭头代表信号削减。神经元的触发阈值用横杠的高低来表示。

异或逻辑运算的规则是，当输入信号是一个0或一个1时，输出信号为1，当输入信号相同时，输出信号为0。设想一下，如果两个输入神经元均静默，则神经网络中没有任何信号传输，输出神经元自然也是静默；如果两个输入神经元中有一个活跃，则会触发隐藏层上侧阈值较低的神经元，然后输出信号传输给输出神经元，则输出神经元活跃；如果两个输入神经元均活跃，则同时触发隐藏层上侧阈值较低的神经元和下侧阈值较高的神經元，隐藏层下侧神经元发送权重较高的削减信号，将隐藏层上侧神经元发送的信号大部分消除，则输出神经元无法达到阈值，则输出静默。

基于数字逻辑元件的神经网络

接下来，就可以用数字逻辑元件搭建神经网络，使其实现异或逻辑运算。一个输入神经元不需要进行阈值判断，所以直接用信号发生器表示即可；隐藏层神经元和输出神经元需要进行阈值判断，可以用信号比较器、信号触发器和信号发生器组合成神经元模块，模块用多个不同的输出表示不同的输出信号权重，在实际应用中，可以选用模块的某一路信号输出，也可以同时使用多路信号输出，具体如图9所示。

最后，将神经元和信号累加器、信号削减器组合起来，成为一个可以实现异或运算的神经网络，如图10所示。可以看出，隐藏层上侧的神经元阈值较低，为二进制数00110，也就是十进制数6，隐藏层下侧的神经元阈值较高，为二进制数01010，也就是十进制数10。当只有一个输入神经元闪烁时，只有隐藏层上侧神经元被触发，最终使得输出神经元收到的闪烁信号频率超过阈值被触发；而当两个输入神经元均闪烁时，两个隐藏层神经元均被触发，下侧神经元的削减信号权重大（通过多个输出累加增加权重），将上侧神经元输出的闪烁大部分削减，则输出神经元收到的闪烁信号频率未超过阈值而保持静默。

用这种基于数字逻辑的神经元当然也可以用来实现更复杂的运算，如判别一个简单的位图到底是数字0还是数字1、进行一位的二进制数加法等。关于实现二进制加法的神经网络结构值得一提，其组成几乎和实现异或运算的神经网络结构一样，仅仅是在输入神经元的信号累加器后接入了一个阈值较高的输出神经元而已（如图11）。只要调整阈值，就能将这个结构用于与逻辑以及或逻辑的运算。至于非逻辑运算，甚至不需要调整阈值，只要直接将两个输入中的一个锚定为1即可。在这里可以看出神经网络实现运算和传统的算法实现运算在方法思路上的区别。

穿越时空的遐想

这里有一个引人遐想的问题，如果将与门和非门串联，则可模拟与非门的功能，继而将四个与非门组合起来就能模拟异或门的功能，那么自然可以先用神经元模拟与非门，再组合起来实现异或门，如图12所示。在20世纪60年代围绕感知机的论战中，是否有人想到用这样简单的方法，就能证明可以使用多个神经元来实现非线性的异或门运算呢？对于这个问题，笔者尚未查找到相关文献，但可以肯定的是，罗森布拉特曾经明确地提出，多层感知机具有单层感知机所不具备的强大的能力。但明斯基却认为“我们尚未发现任何一类真正让人感兴趣的多层机”[1]，其中隐含的意味，大概是认为即便能实现异或运算，也无法实现其他更复杂一些的运算。

罗森布拉特的观点基于一种自然而然的直觉——既然人脑依赖神经元的工作实现智能，那么机器当然也能模仿这一过程，但他既不能严谨地对此加以证明，也难以在现实中加以实施（受制于软硬件条件，当时只能用神经网络解决很简单的问题），罗森布拉特的“非严谨”研究在当时被主流人工智能学界排斥，如今看来是一种很大的损失。直到20世纪80年代，关于多层神经网络是一种普适的模拟器（可以模拟任何函数）的证明才真正完成。[2]还有更多尚没有确切答案但值得展开讨论的问题，如人的直觉是否仅仅是神经元（或其他基础的物理组件）工作过程的产物？未来机器是否可能拥有像人那样的直觉？到底在多大程度上，直觉是可以被信赖的？

参考文献：

[1]Marvin Minsky and Seymour A.Papert.PerceptronsAn Introduction to Computational Geometry[M].Cambridge：The MIT Press，1969：231.

[2]Hornik， Kurt，Maxwell B.Stinchcombe and Halbert L.White.Multilayer feedforward networks are universal approximators[J].Neural Networks，1989：359-366.