基于优化小波分量的高铁桥墩沉降异常探测方法

支君豪,龚循强,杨 忠,鲁铁定,汪宏宇,罗 升

(1.东华理工大学 测绘与空间信息工程学院,南昌 330013;2.东华理工大学 自然资源部环鄱阳湖区域矿山环境监测与治理重点实验室,南昌 330013;3.南昌铁路勘测设计院有限责任公司,南昌 330002)

至2020年底,我国高速铁路已经达到了3.8万km的总里程数,位居世界第一[1]。在高铁桥墩的施工过程中,受线路周边地质等环境影响,可能会引起高铁桥墩发生异常沉降,从而对高铁运营和维护造成较大的影响,甚至威胁到人民生命和财产安全[2]。为了确保高铁的施工和运营安全,防止安全事故发生,保障人民生命和财产安全,有必要针对高铁桥墩沉降观测数据中的异常值进行探测和处理[3]。异常值,也称为离群点,指的是样本中的一些数值明显偏离其余数值的样本点,也可以理解为与大多数数据的分布不一致的数据点[4]。对于高铁桥墩沉降异常值,主要包括人为因素等干扰产生的观测粗差和高铁桥墩受外界因素影响突发形变引起的真实异常值[5]。对于观测粗差将进行剔除,而对于真实异常值则需要根据施工情况进行实地复查等处理。

目前,常规的基于统计学异常值探测方法包括拉依达准则(3σ)法、四分位距(inter-quartile range,IQR)法和中值绝对偏差(median absolute deviation,MAD)法。其中,拉依达准则法在观测次数足够大的前提下,当观测数据服从正态分布时,分别计算观测时间序列数据的平均值和标准差,进而通过判定准则确定异常值,然而异常值的存在会造成观测时间序列数据的平均值和标准差发生偏离,从而导致异常值探测效果不理想[6]。吴浩等提出了一种改进型3σ粗差探测方法,利用小波分解出的高频系数计算得到观测数据的中误差估值σ,结合3σ来评判该点异常的可能性[7]。IQR法是一种简便的统计分析方法,其中位数和四分位距不易受异常值影响,通过稳健Z得分探测观测时间序列数据中的异常值,但当观测时间序列数据离散程度较大时,其四分位间距也会随之增大,导致对偏离程度较小的异常值探测效果减弱[8]。MAD法是一种具有鲁棒性的稳健统计方法,假定观测时间序列数据服从正态分布,通过利用数据中的中位数进行计算,中位数比标准差和平均值更能适应数据中异常值的影响,然而MAD法的参数是通过经验值设置,参数选取较大或较小都会导致探测效果不理想[9-12]。

然而,传统异常值探测方法均存在没有充分挖掘原始时间序列数据的内在发展规律等不足。王威等提出了一种基于小波分析的卫星钟差数据预处理方法,通过对小波分解得到的高频分量和低频分量进行预处理,从而提高异常值探测效果[10]。因此,为有效探测出高铁桥墩沉降监测数据中的异常值,文中提出一种基于优化小波分量的高铁桥墩沉降异常探测方法,通过模拟实验以及工程实例实验,对比分析传统方法和其他组合方法,验证文中方法的有效性和准确性。

1 原理理论与方法

在拉依达准则法的基础上,文中通过对传统异常值探测方法及其它组合方法进行对比研究。下面简要介绍拉依达准则、四分位距法和中值绝对偏差法异常值探测方法原理。

1.1 拉依达准则

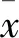
(1)

根据贝塞尔公式求得其标准差s为:

(2)

式中:n为观测样本数量。

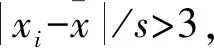
1.2 四分位距法

假设存在一组离散的观测时间序列样本Xn={x1,x2,x3,…,xi,…,xn},将其从小到大依次排序后,根据观测数据中值M和IQR对观测时间序列数据分布进行分析[12]。IQR代表高四分位数和低四分位数之差,计算方法为:

IQR=Q3-Q1.

(3)

式中:Q3、Q1分别为高四分位数和低四分位数。

稳健Zi得分统计量表示为:

(4)

式中:M为观测时间序列数据中位数,SIQR表示为标准化IQR,SIQR=0.741 3×IQR。

当Zi>3时,则认为xi为异常值,反之则认为xi正常。

1.3 中值绝对偏差

假设存在一组观测时间序列样本,Xn={x1,x2,x3,…,xi,…,xn},并服从正态分布,MAD表示为:

MAD=b|xi-median(x)|median.

(5)

式中:b为一个常数,通常取1.482 6[13-14],median(x)为观测时间序列样本x中位数。

观测序列每一个数据对应的Z得分为:

(6)

当Zi>5时,则认为xi为异常值,反之则认为xi正常[10]。

1.4 基于优化小波分量的高铁桥墩沉降异常探测方法

小波分析独特的多分辨率分析性质,使其在信号处理、图像处理与传输等方面应用广泛。小波分析能够对原始信号进行分解从而得到低频近似分量和高频细节分量,从而分离出有效信息和干扰信息,进而进行信号分析[15-16]。其中低频近似分量中主要包含了原始数据的内在发展趋势等特性,而高频细节分量包含原始信号中的瞬态等特性[17-19]。

小波函数是小波分析中的重点环节,小波函数是一种能够迅速衰减到零的一类函数。存在信号f(t)∈L2(R),其连续小波变换(continue wavelet transform,CWT)表示为:

(7)

然而对原始数据进行小波分解会出现低频信号存在噪声和高频信号有效信息提取不充分的问题。因此,为解决此类问题,文中基于小波分析的优势,提出一种利用优化小波分量结合改进拉依达准则法进行异常值探测。图1为沉降异常值探测技术路线,具体步骤如下:

图1 本文所提方法技术路线

1)选择合适的小波基函数和分解层数对原始数据Xn进行小波分解。db5小波基具有较好的正则性和紧支撑性,且能够有效分离有用信息和噪声信息,因此本文选择db5小波基进行实验。选择过高或过低的分解层数都不利于小波进行信号重构,因此需要确定有效的分解尺度[20]。在确定分解尺度的过程中,采用均方根误差(RMSE)作为判断标准,RMSE表示为:

(8)

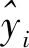
2)利用小波分解获取第1、2层高频分量系数,计算中误差估计σ为:

(9)

3)优化小波分量。在对沉降数据进行小波分解得到低频近似分量系数ai和高频细节分量系数dj后,以低频近似分量系数的中位数m作为判别系数,表示为m=median|ai|,当|ai|>m/3时,则认为该点为异常值,取低频系数中位数对其进行填补;在高频细节分量系数中,计算每一层方差σj=median{|di|/0.674 5},当|dj|>3σj时,则认为该点为异常值,并取该层高频系数中位数对其进行填补。

(10)

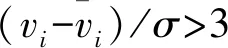
2 实验设计

2.1 模拟实验设计

为了验证文中所提出方法的有效性,通过模拟实验构造高铁桥墩沉降观测数据。在模拟实验中,首先随机生成100组服从正态分布N(0,σ2I)的数据作为原始观测数据,其中σ=0.3,I为单位矩阵。其中模拟实验数据由MATLAB软件生成,如图2所示。

图2 模拟的原始观测数据

根据异常值在观测数据中的数量通常不超过10%的原则[21],文中采用两种方式进行模拟实验:①固定异常值数量为5(即异常值数量占总观测值的5%),系统地改变异常值大小;②固定异常值大小为7σ,系统地改变每次观测量中异常值的数量。为保证模拟实验的可靠性,文中将1 000次重复实验的结果取平均作为最终结果。

2.2 工程实例

文中选取常益长高铁项目沅江特大桥某桥梁墩沉降观测数据作为研究对象。由于沅江特大桥桥梁主跨施工区域水文和地质条件十分复杂,导致获得的观测数据序列不可避免地包含异常值。选取该点位观测日期为2020年11月至2021年2月共87期沉降数据,观测时间间隔为1 d。如图3所示。

图3 原始观测数据

3 实验结果与分析

采用模拟数据和真实数据进行实验,通过对比IQR法、MAD法、拉依达准则法(3σ)、小波分析-IQR法(WT-IQR)、小波分析-MAD法(WT-MAD)、小波分析-拉依达准则法(WT-3σ)、小波分析-中误差估计-拉依达准则法(WT-3σ-ME)和优化小波分量-中误差估计-3σ法(Proposed)对异常值探测效果进行对比和分析。

3.1 模拟实验结果与分析

首先通过模拟实验讨论文中所提方法的有效性。采用文中提出的方法对模拟数据进行异常值探测,并将其与传统异常值探测方法和其它组合方法进行比较。

3.1.1 模拟实验1的结果与分析:异常值大小不同的影响

图4表示在异常值大小不同时不同方法探测得到的异常值数量。从图4中可以看出,随着异常值逐渐增大,所有方法探测出的异常值数量都呈现上升趋势。在探测异常值数量的效果方面,文中方法能够在异常值大小为6σ以上的异常值探测效率接近100%,而其他方法在异常值大小为8σ以上或更大范围的探测效率接近100%,这表明文中所提出的方法在异常值探测效果方面均优于其他方法。在异常值大小从3σ增加到7σ时,由于受到异常值的影响,使得原始数据的中误差偏大,从而造成拉依达准则对偏离相对较小的异常值探测效果不理想;IQR法主要是从时间序列整体发散程度来探查其极端异常值,但忽视了原始数据的潜在发展规律,从而导致对偏离相对较小的异常值不够敏感。文中所提方法是在小波分析的基础上对小波分量进行优化处理,从而能够更加准确地提取原始数据变形趋势,且由小波分解的高频细节分量所计算的中误差估计值不易受异常值影响,相比于传统小波分析组合方法更能体现实际观测精度,从而提高异常值探测的精确度和准确度。

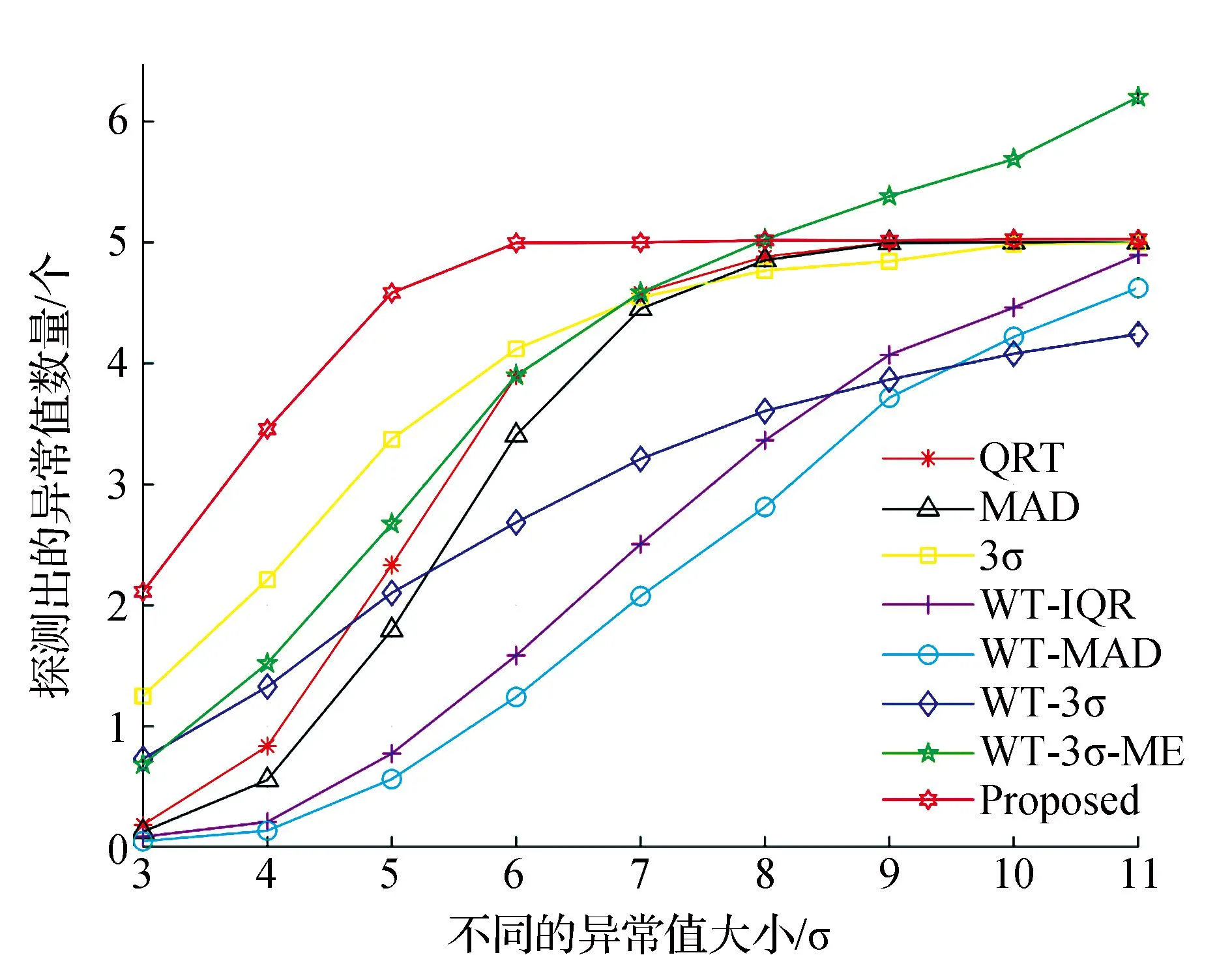
图4 模拟实验中异常值大小不同时探测到的异常值数量

3.1.2 模拟实验2的结果与分析:异常值数量不同的影响

图5表示在每一模拟实验观测量中的异常值数量从1增加至10时,文中所提方法和对比方法所探测到的异常值数量。从图5能够看出文中所提出的方法和IQR法以及MAD法都能够有效探测出大部分异常值,但文中所提出的方法在探测数量方面优于IQR法和MAD法。小波分析-IQR法(WT-IQR)、小波分析-MAD法(WT-MAD)和小波分析-拉依达准则法(WT-3σ)在异常值数量从1增加至5时,3种方法探测的异常值数量逐渐增加,但探测效果并不理想,而当异常值数量从5增加至10时,3种方法的异常值探测数量却逐渐减少;而小波分析-中误差估计-拉依达准则法(WT-3σ-ME)在异常值数量从1增加至9时,探测出的异常值数量逐渐增加,而当异常值的数量从9增加至10时,探测出的异常值数量逐渐减少,这是因为这4种方法在对原始数据进行小波分析后得到的低频分量存在噪声和高频分量未被利用的有效信息。而拉依达准则法在异常值数量从1增加至7时,探测出的异常值数量逐渐增加,但对异常值也不够敏感且在异常值数量从7增加至10时,探测出的异常值数量逐渐减少,这是因为随着异常值数量的增加,异常值会对原始数据的中误差产生较大偏离从而导致探测效果不理想。

图5 模拟实验中异常值数量不同时探测到的异常值数量

3.2 工程实例结果与分析

从图2可以看出,原始观测数据中的异常值的范围较大,分布相对较为离散。文中分别采用IQR法、MAD法、拉依达准则法、小波分析-IQR法(WT-IQR)、小波分析-MAD法(WT-MAD)、小波分析-拉依达准则法(WT-3σ)、小波分析-中误差估计-拉依达准则法(WT-3σ-ME)和优化小波分量-中误差估计-拉依达准则法(Proposed)对图2所示的观测时间序列数据进行异常值探测,与模拟实验相同,采用db5小波基进行实验,根据式(7)求得最佳小波分解层数均为2,探测结果如表1所示。图6为文中方法在沉降观测数据中的异常值探测结果。

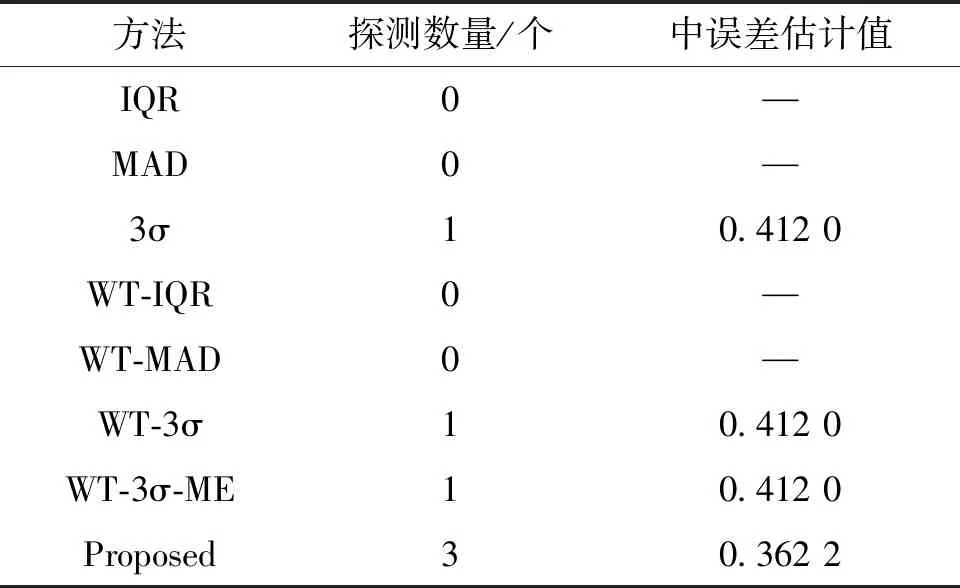
表1 工程实例的异常值探测数量及中误差估计值

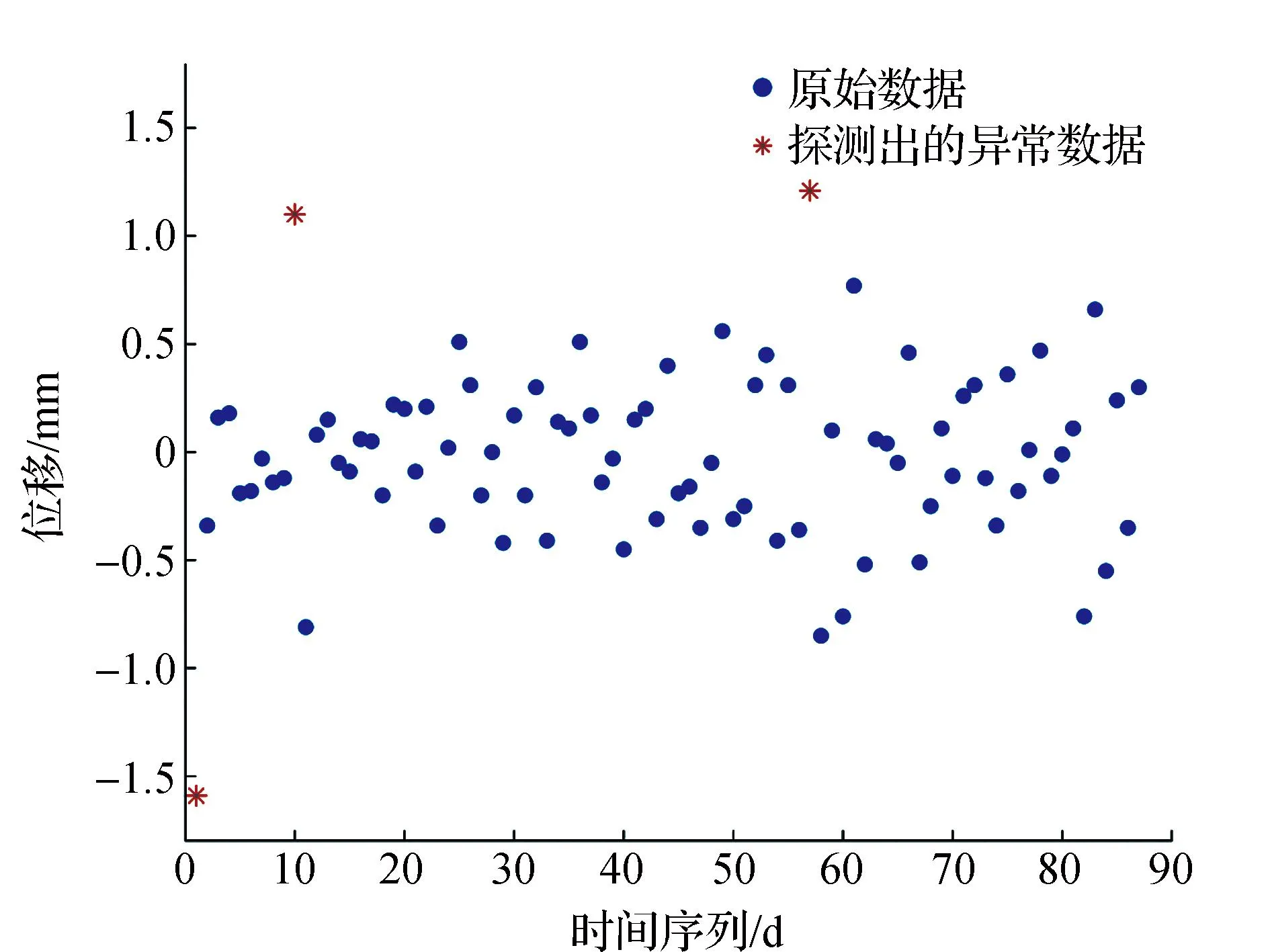
图6 文中方法沉降观测数据异常值探测结果

从表1可以看出,IQR法、MAD法、WT-IQR法和WT-MAD法并不能够探测出原始数据中存在的异常值,3σ法、WT-3σ法以及WT-3σ-ME法仅探测出一个异常值,而文中所提出的方法能够有效探测出更多的异常值。从图6可以看出,文中方法对偏离程度较小的异常值也能够进行有效探测。为了进一步验证文中探测方法的有效性,分别计算了3σ法、WT-3σ法、WT-3σ-ME以及文中方法的中误差估计值。在探测出的异常值数量方面,文中方法探测出的异常值数量优于其它方法;在计算的中误差估计值方面,文中方法计算得到的中误差估计值优于传统方法及其它小波组合方法,相比于其它方法的中误差值降低了12.09%,降低了残差受异常值干扰而不能正确得到中误差估计值的影响,说明文中方法更加稳健,进一步表明采用文中方法进行异常值探测更加有效。

4 结 论

由于高铁桥墩沉降观测条件的不稳定性和复杂性,可能会遇到沉降观测数据中存在部分异常数据的情况,然而常规的基于统计学的异常值探测方法探测结果并不理想。为了解决这一问题,提出了一种基于优化小波分量的高铁桥墩沉降异常探测方法。通过模拟实验和工程实例进行对比和分析,结果表明文中所提出的方法在保证能够有效探测出异常值的同时,对偏离程度较小的异常值探测效果明显,相比于单一方法具有较大的优势,能够更好适应高铁桥墩沉降观测项目需求,具有一定的实际应用价值。