基于ARIMA-LSTM混合模型对传染病的预测分析

王瑞 李瑞沂 曹沛根 冯和棠 黄猛

DOI：10.19850/j.cnki.2096-4706.2024.01.024

收稿日期：2023-01-16

基金项目：防灾科技学院2022大学生创新创业项目（202211775011）

摘  要：传染病一直是科学研究的热点，利用科学的方法控制传染病的传播对整个国家乃至全世界具有举足轻重的作用。文章选取乙类传染病中新型冠状病毒感染数据作为研究对象，搜集了北京市2022年1月至2022年4月新冠感染累计确诊病例数，构成时间序列，基于自回归移动平均模型（ARIMA）和长短期记忆神经网络（LSTM）的混合模型进行预测分析。结果表明，混合模型的预测结果与实际情况基本一致。

关键词：时间序列；ARIMA模型；LSTM模型；组合预测模型

中图分类号：TP391    文献标识码：A  文章编号：2096-4706（2024）01-0116-05

Prediction Analysis of Infectious Diseases Based on ARIMA-LSTM Mixed Model

WANG Rui， LI Ruiyi， CAO Peigen， FENG Hetang， HUANG Meng

（Institute of Disaster Prevention， Langfang  065201， China）

Abstract： Infectious diseases have always been a hot topic in scientific research， and using scientific methods to control the spread of infectious diseases plays a crucial role in the entire country and even the world. This paper selects COVID-19 infected persons in class B infectious diseases as the research object， collects the cumulative number of confirmed cases of COVID-19 infection in Beijing from January 2022 to April 2022， forms a time series， and conducts prediction analysis based on a mixed model of autoregressive moving average model （ARIMA） and Long Short-Term Memory （LSTM）. The results indicate that the prediction results of the mixed model are basically consistent with the actual situation.

Keywords： time series; ARIMA model; LSTM model; combinatorial prediction model

0  引  言

自2020年12月新冠疫情暴發以来，全球多数国家均陷入疫情风波，为了抗击疫情，我国不断调整疫情防控政策，一次又一次渡过难关。可新冠病毒来势汹汹、变化不定且蔓延范围广，为了保证国家的正常发展和人民的稳定生活，国家只能不断完善疫情防控政策。由此可见，新型冠状病毒感染作为典型的呼吸道传染疾病具有很大的研究价值，如果能对其进行深入研究，发现其发展的规律性，那么我们对流行传染病的研究将向前跨一大步。当对新型传染病的疾病动态尚不清楚的时候，我们常使用数学模型进行研究，数学模型不仅能估算最坏情况下的感染人数，对所采取的预防措施的效果进行评估，还可以帮助人们理解流行传染病的复杂性，并提供针对性的解决方案，因此利用数学模型来预测流行传染病的发展趋势十分必要。由于传染病的传播受多种因素影响，数学模型中关于这些因素的假设和模型中设置的参数值都会影响预测结果，因此选取模型和参数尤为重要。

鉴于此，本文以新冠疫情暴发后北京市产生的确诊病例构成时序数据，利用混合模型ARIMA-LSTM对该数据进行研究，预测出未来短期内的新冠疫情的发展趋势，从而发现传染病传播发展的规律性，这不仅有利于国家更好地制定防疫计划，还能为科研人员研究流行传染病提供有力的参考依据。

1  研究现状

传染病始终存在于人类生存和发展过程中，是全人类不得不面对的一大难题。许多来自不同专业领域的科研人员投身其中，不断推进着对传染病传播的研究。早期适用性较好且使用较多的算法有基于指数函数的趋势预测方法、多元回归算法等，随着科技的发展和深度学习的火爆，不少研究在传统传染病模型的基础上增加了基于神经网络模型和基于时间序列的预测方法。

1.1  传统传染病模型

目前比较常用的传染病模型有SIR[1]和SEIR[2]，这两个模型都常用于研究传统传染病，通过构建微分方程的方式，对传染病传播的发展进行参数计算、模拟和预测等操作。黄森忠等[3]基于SEIR模型，判断疫情发展趋势，明确2020年初疫情的基本参数，如基本再生数、平均潜伏期等；杨赟等[4]考虑到现实生活中时常会有一些随机突发情况，因此他们利用马氏过程模拟新冠疫情的传播过程，通过转移概率来模拟新冠疫情在不同舱室传播的可能性，建立出随机SEIR模型。

传统的传染病模型可以预测未来的感染数量，从而有效地预防和控制传染病，但其建立过程和模型参数获取相对复杂。因此，部分研究利用简单易操作的单一预测模型进行相关的传染病预测分析。

1.2  单一预测模型

巴艳坤等[5]选取了挪威地区2021年7—9月的COVID-19累计感染人数，使用基于麻雀搜索算法（SSA）优化过后的BP神经网络模型进行研究。白璐等[6]通过机器学习的分析方法建立ARIMA模型，通过模型分析对湖北省未来确诊人数进行预测。盛华雄等[7]分析武汉封城前这段时间的疫情，利用Logistic模型模拟了提前5天或延后5天实施隔离政策的情况，从而得到引起新冠疫情发展趋势变化的曲线。

在单一模型中，数据信息提取不足，大样本数据分析效果差，导致预测效果与实际数据误差较大。因此，一些研究开始结合单一模型的优点，避免其缺点，使用组合模型使预测值更接近真实情况。

1.3  组合预测模型

张晴等[8]将传染病模型SIR和逻辑回归模型Logistic相结合，并在考虑到线性模型的局限性后，加入了时间卷积神经网络TCN，但TCN模型有时不太稳定，需要进一步优化。董章功等[9]人基于SEIR和ARIMA构建的传统传染病动态混合模型SEIR-ARIMA预测了不同时间和地点的COVID-19感染人数，但该混合模型尚未研究更复杂的情况，比如康复者是否会再次感染等，因此具有一定局限性。甘雨等[10]提出结合SEIR和LSTM，预测疫情发展趋势，预测结果优于传统SEIR模型。

从以上研究结果可以发现，使用单一的传统传染病模型或时间序列模型都存在限制条件太多、模型复杂时参数选取困难、模型简单时预测效果差等问题，将模型之间进行组合后能在一定程度上弥补单一模型的某些缺点，使研究结果更有说服力。由于在组合模型的应用研究中，基于ARIMA-LSTM混合模型对局部流行病传播的预测分析比较少见，因此本文运用该混合模型对传染病传播进行研究。

2  ARIMA模型

ARIMA差分整合移动平均自回归模型是一种应用广泛的经典时间序列模型。该模型中，共有三个参数，分别是p（自回归阶数）、d（差分阶数）和q（移动平均阶数），大致为以下形式：

其中，yt为时间序列，如果该时间序列不具稳定性，一般先采用ADF检验，选取差分阶数后将yt变平稳，再结合赤池信息准则AIC和贝叶斯信息准则BIC对模型进行最佳参数选择。

3  LSTM模型

长短时记忆神经网络（LSTM）是循环神经网络的一个变体，对长期依赖问题和梯度消失的问题能有效解决，该模型的关键是引入一组记忆单元（Memory Units）允許Web学习何时忘记历史信息，何时用新信息更新记忆单元，并由3个“门”控制：输入门it，遗忘门ft和输出门Ot。

式中，Wf、Wi、Wo、Wc分别为遗忘门、输入门、输出门、输入门和中间变量与当前时刻输入Xt和上一时刻输出ht-1作乘法运算的权重，bf、bi、bo、bc为偏置向量。

4  ARIMA-LSTM混合模型

ARIMA模型作为一种经典的时间序列预测模型，可用于时间序列的随机平滑建模和预测，但它在分析过去与未来数据之间的联系时去掉了事物发展的因果关系。LSTM神经网络能记忆大量的长期数据，常用于处理时序时间序列。因此，本文首先使用ARIMA提取线性信息，预测线性结果的第一部分，并计算残差序列；然后将第一部分生成的残差序列输入LSTM模型，生成第二部分的非线性结果。最后，将两部分预测结果相加，得到最终的预测值。

5  实验分析

5.1  实验数据采集

在数据采集方面，本研究采用爬虫技术采集百度疫情提供的北京市2022年1月2日至4月20日的新冠感染确诊人数，建立时间序列数据，分析北京市疫情发展趋势，如表1所示。

5.2  数据预处理

5.2.1  平稳性检验

在采集的109条数据中，选取其中2022年1月2日至4月15日COVID-19的感染人数作为训练集数据，绘制序列图如图1所示。

从训练集时序图可以看出均值在随时间变化而变化，但仅凭肉眼看不能有力证明该训练集数据的非平稳性，因此为了进一步加强该时间序列非平稳的假设，接下来进行ADF测验。验证结果如表2所示。

从理论和实战经验中了解到，如果一个时间序列是平稳的，那么它的ADF测试结果中的p值应较低，并且1%、5%和10%置信区间的阈值应尽可能接近Test Statistic这个属性值。但从以上ADF检验结果可以看出，p值不够小，临界值与检验统计量也不够接近，因此可以得出该时间序列目前处于非平稳状态。

5.2.2  数据的平稳性处理

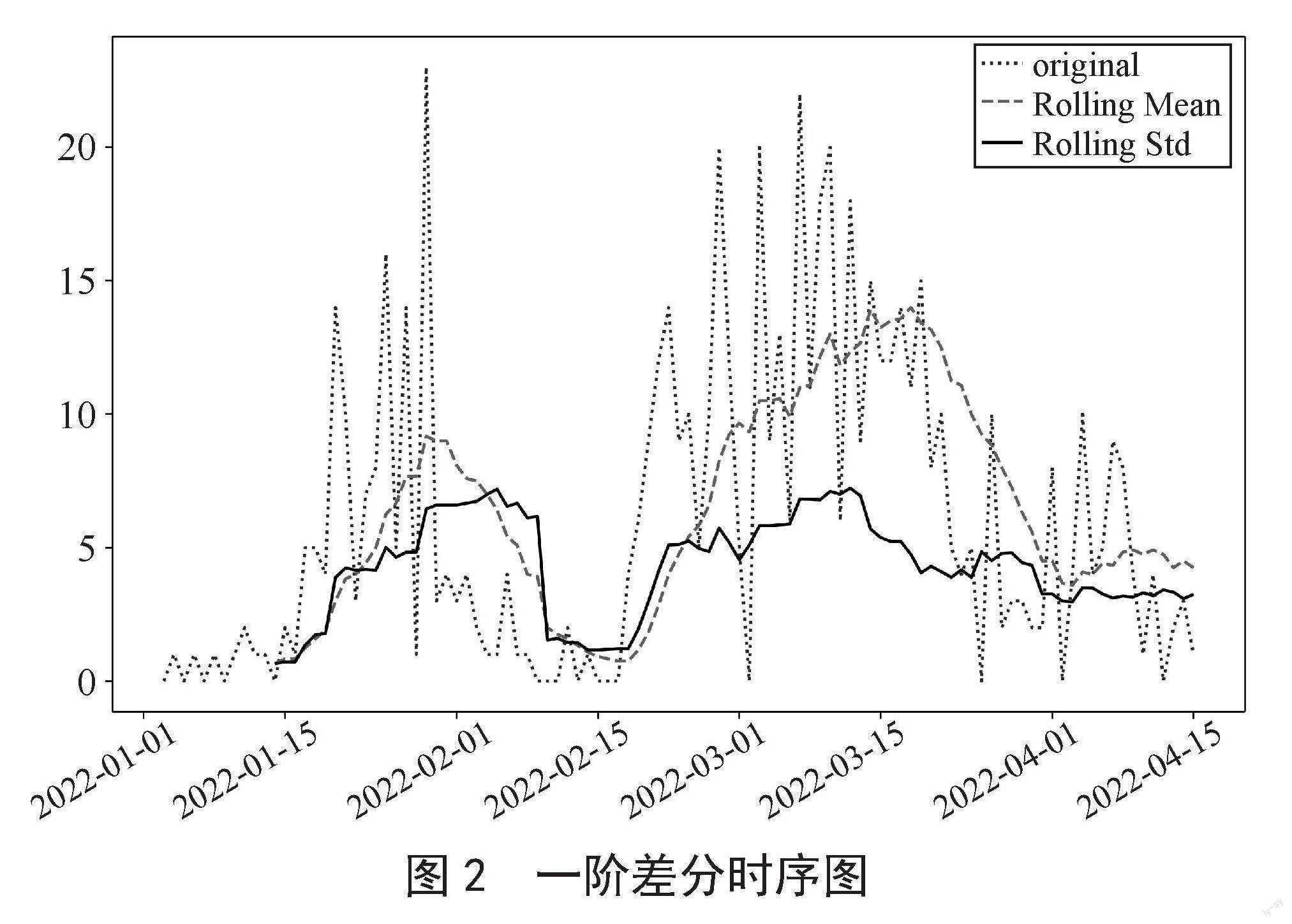
通常情况下，把时序数据应用于ARIMA模型时，需要确保平均值和均值随时间变化保持不变，为了达到该目的，本文采用目前常用的处理非平稳序列的手段差分处理，但由于“过差分”容易造成资讯的流失，因此本文逐阶进行差分处理。首先进行一阶差分处理?yt = yt - yt-1，做出一阶差分后时序图，如图2所示。

图2  一阶差分时序图

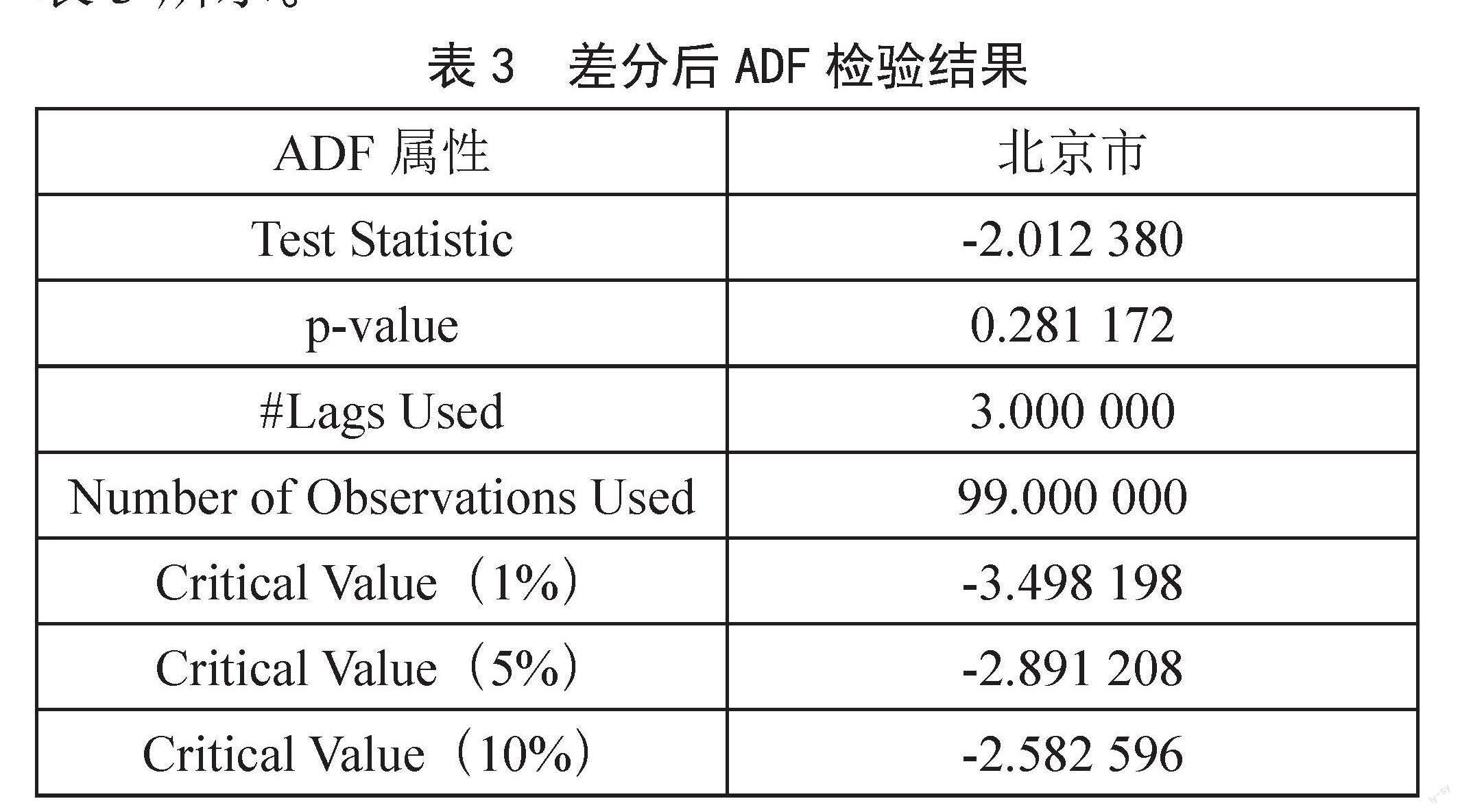
从这张图中，我们大致可以看到，原始数据中的增长趋势已经通过差分运算提取出来，序列应该是大致稳定的。为了帮助我们更客观地判断序列是否稳定，我们对差分后的数据进行ADF单位根检验，结果如表3所示。

从表3中可知，ADF结果值都是显著小于Test Statistic检验统计量，则认为在置信水平为95%的情况下无单位根，说明一阶差分后序列是平稳的，可进行后续分析。

5.3  ARIMA模型构建

5.3.1  确定模型阶数

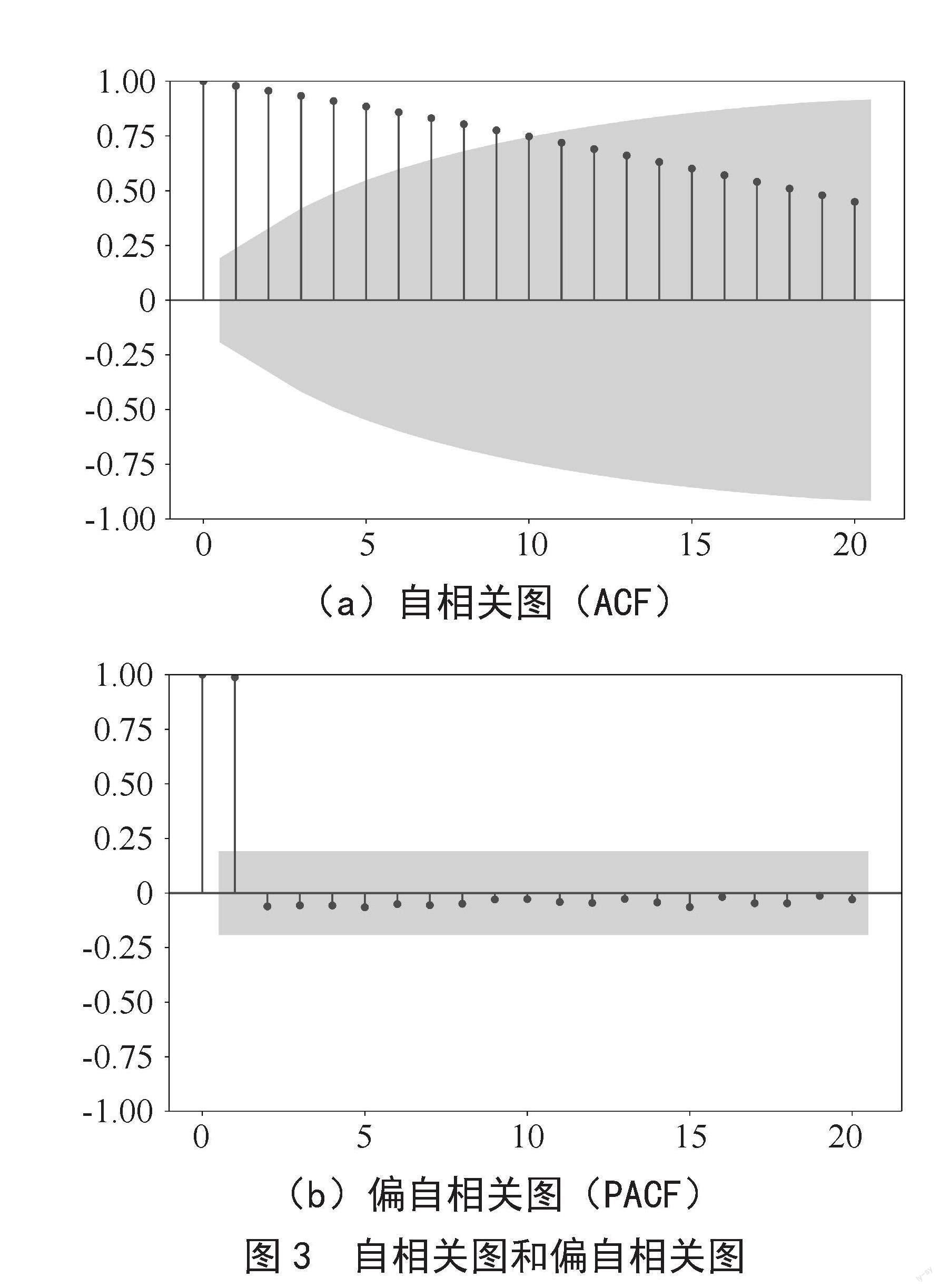
通常ARIMA（p，d，q）模型的p和q值是通过自相关图和偏自相关图来确定的，但这种判断比较主观。因此，本文的具体定阶方法如下：根据自相关图和偏自相关图判断阶的近似范围，然后利用AIC和BIC信息准则选择更准确的模型，如图3所示。

其中，横坐标为滞后阶数，纵坐标为相关系数。

从图3可以看出，ACF和PACF经过2阶滞后后，在2倍标准差范围内基本稳定。但由于判断图像呈拖尾还是截尾主观性太强，因此我们通过Python的sm库中的arma_order_select_ic方法，计算出最优的AIC的BIC，即挑选出最佳模型ARIMA（2，1，2），模型结果如图4所示。

图4  模型调试结果

根据图4我们发现：依据AIC和BIC挑选出来的模型并非完全符合实际，因为第二个非常量参数的p值为0.162，大于0.05，显然没有通过参数检验。所以，ARIMA（2，1，2）的拟合效果并不完美。这表明上述数据的ARIMA建模仍有改进的空间，为LSTM模型的建立提供了基础。

5.3.2  建立模型和预测结果

使用上述ARIMA（2，1，2）模型进行相关预测。模型残差拟合效果图及相关预测结果如表4所示。

为了更直观地反映模型的预测精度，我们选用衡量指标均方误差MSE来反映误差。MSE值越小，实际值与预测值之间的差距越小。结合公式  得到MSE为3.476，可见误差比较小，说明ARIMA模型的预测精度还是可以接受的，具有一定的指导意义。

5.4  LSTM模型构建

5.4.1  数据处理

在本文中，67%的数据作为训练数据集用于训练LSTM模型，剩余33%的数据作为测试数据用于测试模型。然后利用归一化过程将训练集数据标准化到0～1的范围内，使模型训练效果更好。

5.4.2  模型训练

LSTM模型的训练过程如下：

1）输入训练集，得到初始权值。

2）利用验证集反向优化权重。

3）训练最佳模型。

由于Python中的TensorFlow库已经将LSTM模型算法封装完毕，我们只需投入数据，设置好相关参数进行调用即可。其中核心参数的设置如下：epochs=500，batch_size=1，verbose=2。

最后运行结果显示整体损失率大致范围为1%～

4%，这说明利用该训练模型进行预测效果尚可。

5.5  ARIMA-LSTM结合预测

ARIMA-LSTM结合预测过程如下：

1）通过ARIMA模型得到数据的残差序列，如图5所示。

图5  残差序列图

2）将残差序列输入经过良好训练的LSTM模型，得到这部分非线性信息的预测值。最后将该预测值与ARIMA相加，得到诊断病例数的预测值，并得到最终结果，如图6和表5所示。

到目前为止，我们发现单个ARIMA模型的均方误差为3.476，混合ARIMA-LSTM模型的均方误差为3.161。由此得出结论：混合模型的预测精度略高于单一时序模型ARIMA。

6  结  论

综上所述，ARIMA（2，1，2）与LSTM神经网络混合模型能较好拟合北京市新型冠状病毒短期流行趋势，因此在进行传染病预测研究时可选取该混合模型进行一定程度的分析，为政府制定相关防疫政策提供合理有效的参考。本研究下一步将考虑如何在ARIMA-LSTM混合模型的基础上将预测结果准确率大幅提升。

参考文献：

[1] 刘乙阳，黄洋，尹澜瑜，等.基于SIR模型的流行性传染病传播趋势预测研究 [J].高师理科学刊，2021，41（7）：37-41.

[2] 马思婕，黄珈铭，印英东，等.基于SEIR模型的COVID-19传染力研究 [J].江苏科技信息，2022，39（10）：73-76.

[3] 黄森忠，彭志行，靳祯.新型冠状病毒肺炎疫情控制策略研究：效率评估及建议 [J].中国科学：数学，2020，50（6）：885-898.

[4] 杨赟，赵亚男.基于随机SEIR模型的新冠肺炎傳播动力学分析 [J].东北师大学报：自然科学版，2022，54（4）：37-43.

[5] 巴艳坤，郭松林.基于BP神经网络的新冠肺炎疫情病例预测模型 [J].电脑知识与技术，2022，18（20）：78-80.

[6] 白璐，郭佩汶，范晋蓉.湖北省新冠肺炎确诊人数的建模与预测分析 [J].检验检疫学刊，2020，30（2）：10-12.

[7] 盛华雄，吴琳，肖长亮.新冠肺炎疫情传播建模分析与预测 [J].系统仿真学报，2020，32（5）：759-766.

[8] 张晴.关于新冠肺炎疫情的研究和预测 [D].济南：山东大学，2021.

[9] 董章功，宋波，孟友新.基于SEIR-ARIMA混合模型的新冠肺炎预测 [J].计算机与现代化，2022（2）：1-6.

[10] 甘雨，吴雨，王建勇.新冠肺炎疫情趋势预测模型 [J].智能系统学报，2021，16（3）：528-536.

作者简介：王瑞（2001—），女，汉族，四川宜宾人，本科在读，研究方向：计算机科学与技术。