基于变分模态分解和稀疏表示的局部放电信号去噪算法

钟俊 刘桢羽 赵晓坤 唐妮妮 毕潇文

DOI：10.19850/j.cnki.2096-4706.2024.01.016

收稿日期：2023-10-19

摘  要：鉴于局部放电信号受各种噪声的干扰，文章提出一种基于变分模态分解和稀疏分解的局部放电信号去噪算法。以稀疏表示算法为核心，基于局部放电信号的特性构建其过完备字典，再采用匹配追踪算法在过完备字典中搜索出原信号的最佳匹配原子集合重构信号；为解决过完备字典维度过高而导致的搜索次数太多的问题，引进变分模态分解算法和峭度值筛选进行预处理和预重构；优化后的方法可以限制稀疏分解算法的搜索范围和字典参数，以减小计算复杂度。仿真验证以及对工程环境中实测信号的去噪结果表明：该方法具有更好的降噪效果，即使在极低信噪比的情况下，依旧能提取出有效的局部放电信号。

关键词：局部放电信号；变分模态分解；峭度；稀疏表示；机器学习；匹配追踪算法；自适应

中图分类号：TP391.4  文献标识码：A  文章编号：2096-4706（2024）01-0077-07

Partial Discharge Signal Denoising Algorithm Based on Variational Modal Decomposition and Sparse Representation

ZHONG Jun1， LIU Zhenyu1， ZHAO Xiaokun2， TANG Nini2， BI Xiaowen1

（1.College of Electrical Engineering， Sichuan University， Chengdu  610065， China;

2.State Grid Chengdu Power Supply Company， Chengdu  500642， China）

Abstract： Considering the interference of various noises on partial discharge signals， this paper proposes a partial discharge signal denoising algorithm based on variational modal decomposition and sparse decomposition. Based on the characteristics of partial discharge signals， the sparse representation algorithm is used as the core to construct an overcomplete dictionary， and then the matching and tracking algorithm is used to search for the best matching atomic set of the original signal in the overcomplete dictionary to reconstruct the signal; to solve the problem of excessive search times caused by excessive dimensionality in an overcomplete dictionary， the variational modal decomposition algorithm and kurtosis value screening are introduced for preprocessing and pre reconstruction; the optimized method can limit the search range and dictionary parameters of the sparse decomposition algorithm to reduce computational complexity. Simulation verification and denoising results on measured signals in engineering environments show that this method has better denoising effects， and can still extract effective partial discharge signals even in extremely low signal-to-noise ratios.

Keywords： partial discharge signal; variational modal decomposition; kurtosis; sparse representation; Machine Learning; matching and tracking algorithm; self-adaption

0  引  言

局部放電（Partial Discharge， PD）是电气设备状态在线监测的重要组成部分，它能够准确反映电气设备绝缘老化的严重程度[1]。电气工程师可以通过局部放电信号评估高压设备的安全性和稳定性。然而，由于高压放电环境的复杂性，局部放电信号不可避免地会受到各种类型噪声的污染，其中白高斯噪声和窄带噪声对局部放电信号影响最为显著[2]。目前，学者们主要的研究方向在：去除局部放电信号中的噪声和干扰，明确其脉冲的边界，并准确提取局部放电信号的形态。

在局部放电信号的研究中，目前已经有多种方法可以减少白噪声和窄带噪声。主要包括FFT阈值滤波法、自适应数字滤波法、经验模态分解（Empirical Mode Decomposition， EMD）、小波分析法，以及近几年新兴的奇异值分解方法（Singular Value Decomposition， SVD）。FFT阈值滤波法和自适应的数字滤波法是经典的信号降噪算法，这两种算法只能一定程度上去除噪声，且效果及其不稳定[3]。EMD相较于FFT阈值滤波法和自适应的数字滤波法具有更好的降噪效果，但模态混叠和边界效应是一直都是EMD中需要解决的问题。EEMD（Ensemble Empirical Mode Decomposition）在传统EMD算法上加入了一个噪声辅助的技术。准确地说，EEMD是通过为数据添加一个小的白噪声集合来强化局部特性，从而达到更加稳定和准确地实现模态分解，能够帮助避免模态混叠[4]。但是，去噪效果不稳定这个问题依旧存在。小波变换也是一种经典的改进型局部放电信号噪声减少方法。近年来，有研究采用自适应阈值小波进行噪声降低，取得了不错的效果[5]。只是小波的降噪效果取决于其母小波。此外，如何对于各种不同且复杂母小波建立统一阈值也一直是一个研究难题[6]。奇异值分解方法也可用于噪声降低。自适应奇异值分解（Adaptive Singular Value Decomposition， ASVD）[7]和稀疏奇异值分解（Sparse Singular Value Decomposition， SSVD）[8]是两种典型的改进SVD方法。SVD和改进SVD方法的目标都是通过提取有用信号和噪声的不同奇异值来消除噪声[9]。

稀疏表示理论是一种在机器学习、计算机视觉、模式识别等领域广泛被使用的高级人工智能算法[10]。信号稀疏表示的核心思想是从一个超完备的字典中选取最为简约的基函数组合来描述原始信号。在工程信号中，稀疏分解算法的应用比较少见，曾经在OFDM系统中有过一些应用[11]。在局部放电信号中，稀疏分解算法的应用更加少见。Thome和Silva使用小波族构建了局部放电信号的过完备字典[12]，但这种基于小波族构建的过完备字典的过程并没有展现出PD信号的特性。

本文通过原始无噪声PD信号的结构特征创建了脉冲匹配原子，将这些脉冲匹配原子离散化组成PD信号的过完备字典。这些脉冲匹配原子与原始局部放电信号具有高度相关性，并且与噪声无相关性，接着就可以使用匹配追踪法（Matching Pursuit， MP）算法在这个过完备字典中搜索原始无噪PD信号的最佳匹配原子，并使用选定的最佳匹配原子来重构PD信号。通过这样的方法，噪声就变成了残差被丢弃掉，而原始无噪的PD信号被重构了出来。然而，在成功构建PD信号的过完备字典后发现，这个过完备字典是高维的；那么在应用MP算法进行搜索的时候，计算量是非常大的。也就是说如果直接对PD信号应用稀疏分解和重构算法，那么算法的效率就会很低。为了解决这个问题，就需要减少搜索次数，提高计算效率。实验显示，局部放电信号通常是由一些瞬时放电脉冲组成。这些短放电脉冲，只占整个时域非常小的部分，而不加任何限制的稀疏分解算法是对整个时域进行搜索。如果能够找到局部放电信号脉冲的起始点和结束点、时频特性，对信号的参数进行限制，同时只在这些脉冲存在的时域范围内进行搜索，计算复杂性将大大降低。

为了优化算法，本文使用变分模态分解（Variational Mode Decomposition， VMD）算法来缩减搜索范围并提高算法效率。VMD是一种有效的信号去噪方法，已被证明可以在不影响原始无噪声局部放电信号波形结构的情况下去除大部分噪声[13]。同时，与EMD和EEMD相比，VMD具有更好的预处理降噪效果[14]。同时，由于VMD算法是给予噪声和信号的中心频率进行模态分解，使用峭度重构后的信号时频特性也可以显现出来。在此之后，稀疏分解算法就可以对搜索的范围进行自适应的限制，进一步对信号进行降噪，得到干净无噪的局部放电信号。

本文在确定了算法思路后，对本文提出的方法进行了仿真模拟，其结果表明本文提出的方法具有明显的降噪效果。本文还展示了其他3种方法（硬阈值小波、EEMD和SSVD）的降噪效果。对比结果表明，与传统的降噪技术相比，本文提出的算法能够更好地提取局部放电信号。

1  稀疏表示

Mallat和Zhang在1993年首次提出了信号的稀疏表示[15]。他们基于小波技术提出的稀疏表示算法和匹配追踪法，其原理如下：

首先，假设原始信号S的长度为N。然后，需要构建一个过完备的字典集合。定义一个集D = {gγ，γ = 1，2，3，…，γ}，γ＞N，然后将集合D中的所有元素扩展到希尔伯特空间H = RN。这样，集合D就可以作为原始信号的过完备字典，其中所有元素gγ都是字典的匹配原子。接着，在集合D上应用MP算法对信号S进行稀疏分解算法：

MP算法的主要作用是在字典中寻找最佳匹配原子 ，满足以下条件：

（1）

其中， 表示原始信号S和最佳匹配原子  的内积； 表示与原始信号S方向最接近的原子； 表示在希尔伯特空间中与信号S最匹配的原子。

接着，原始信号就可以分解为两部分，再不停对残差进行分解：

（2）

（3）

其中， 表示原始信號S在最佳匹配原子  上的投影；而R2S是在原始信号S初步分解后的残差。

接着，对残差R进行相同的分解处理，直到达到停止条件。

信号稀疏表示中有两种方法来设置停止条件。第一种方法是直接设置迭代次数。当达到预定的分解次数时，迭代过程将自动结束。第二种方法是使用残差的二范数  作为迭代终止条件。着当残差的二范数小于某个预先设定的阈值δ时，算法将停止迭代。

迭代停止后，原始信号可以用来自过完备字典的K个最佳匹配原子进行表示：

（4）

2  VMD算法

2.1  VMD算法

Dragomiretskiy等人在EMD算法的启发下提出了VMD算法。EMD通过对信号进行包络和迭代将其分解为固有模式；而VMD则构建了一个变分问题模型，通过求解该模型将信号同时分解为多个有限带宽的模式，其中每个模式成分都有其相应的中心频率[16]。

VMD的数学思想是将VMD将一个实值输入信号分解为K个有限带宽的模式μk，所有模式μk的和等于原始输入信号，并且应该尽量被最小化。该约束优化变分问题表达式如下：

（5）

其中，x（t）表示原始输入信号；μk（t），ωk表示BLIMF以及它们的中心频率；δ（t）表示费米-狄拉克（Fermi-Dirac）分布函数； 表示通过对每个模式μk（t）进行Hilbert变来估计BLIMF的带宽。

通过引入增广Lagrange函数?和二次惩罚因子α，这个约束问题可以被转化为：

（6）

最后，连续初始化{μk}，{ωk}，λ，找到增广Lagrange函数?的鞍点，当迭代停止后，通过逆傅里叶变换可以得到满足式（5）的K个模态函数。

2.2  峭度

峭度是一个无量纲的因子，用来评估信号偏离正态分布的程度[17]。峭度的计算式如下：

（7）

其中，x（t）表示瞬时幅度； 表示平均幅度；p（t）表示概率密度函数；σ表示标准差。

3  基于过完备字典的PD信号去噪

3.1  PD信号的过完备字典的构建

研究表明，原始无噪的PD信号包含4个典型模型[18]：

1）单指数衰减模型：

（8）

2）双指数衰减模型：

（9）

3）单指数振荡衰减模型：

（10）

4）单指数振荡衰减模型：

（11）

其中，τ表示衰减常数；fc表示震荡常数。

根据式（8）至式（11），可以发现PD信号具有三个基本参数：尺度、频率和相位。因此，可以相应的构建三个PD信号基本因子：s（尺度因子）、ω（频率因子）和φ（相位因子）。此外，由于PD信号由四种类型的波形组成，还需要一个波形因子η来描述这些波形之间的关系。然后，就可以以下匹配原子集合ργ：

（12）

其中，A表示用于归一化的频谱参数；k表示衰减校正系数，用于修正当尺度因子s过大时，局部放电信号的匹配原子与正弦信号难以匹配的情况，并有效地消除窄带周期性干扰对PD信号的影响。

假设信号的采样长度为N，将匹配原子集合离散化，其中，将基本因子（s，ω，φ，η）离散化为 ，就可以得到基于PD信号构建的过完备字典：

（13）

式中：n ∈ [0，N]；ns ∈ [1，N]；nω ∈ [0，N-1]；nφ ∈ [0，1]；nη ∈ [0，1]；ns，nω，nφ，nη ∈ Z。

到这里PD信号的过完备字典就被成功构建，该字典并且拥有超过  个原子，满足了冗余性的要求。然而，在这个三维过完备字典中存在太多的原子。随着采样次数N的增加，搜索量将会呈现立方级增长。

3.2  基于VMD和峭度的算法优化

为了减少搜索次数，减少计算数量并提高效率，过完备字典的搜索范围应该得到限制。从PD原始无噪声信号的特性可以看到，PD信号并没有分布在整个时域中，只在很短的时间段内有少量脉冲信号存在，因此算法只需要在这些时间段内使用即可。通过这样的限制，计算数量可以大幅减少，从而显著提高算法的效率。

然而，在工程环境中，原始PD信号总是被噪声所掩盖。参杂了高斯白噪声和窄带噪声的含噪PD信号是很难直接被区分出来，更无法直接确定其放电范围。

这个问题本文通过VMD算法来进行解决。VMD算法可以将信号分解成一系列带有中心频率的有限带宽模态，同时对噪声具有鲁棒性。由于噪声和原始无噪PD信号的中心频率具有很大差异，因此在PD信号上使用VMD分解并通过峭度选择模态进行重构，并不会改变PD信号特性，又可以有效去除噪声。经由VMD算法去噪后的PD信号，就可以确定其起始和终止放电点Non和Noff，以及中心频率fc和带宽B，并将因子范围限定如下：

（14）

其中，f表示采样频率。

在此之后，就可以用稀疏分解算法去除残余的噪声，其流程图如图1所示。

4  仿真验证与分析

信号的仿真模型是通过上一章提到的四种模型混合组成。参数如下：单指数振荡衰减模型和双指数振荡衰减模型的振幅A = 0.8 mV，3 mV；衰减系数τ = 0.02 μs，0.03 μs；振荡频率fc = 50 MHz；采样频率为1 MHz。图2中展示了模拟的无噪声PD信号。

然后，在模拟的PD信号中加入-10 dB高斯白噪声和窄带噪声，使PD模拟信号更接近工程环境中的实际信号。工程环境中的窄带噪声主要包括载波通信干扰和广播通信（中频段0.5～1.6 MHz，短频段2.3～

25 MHz，FM 88～108 MHz频段）。通过组合不同振幅的正弦信号，就可以一定程度上模拟窄带噪声。本文将模拟窄带干扰的频率设定为9 MHz、14 MHz和96 MHz。将噪声叠加在原始PD信号，可得到仿真含噪PD信号如图3所示。

从图3中可以看出，原始PD信号（粗线）已经被完全淹没在噪声之中。

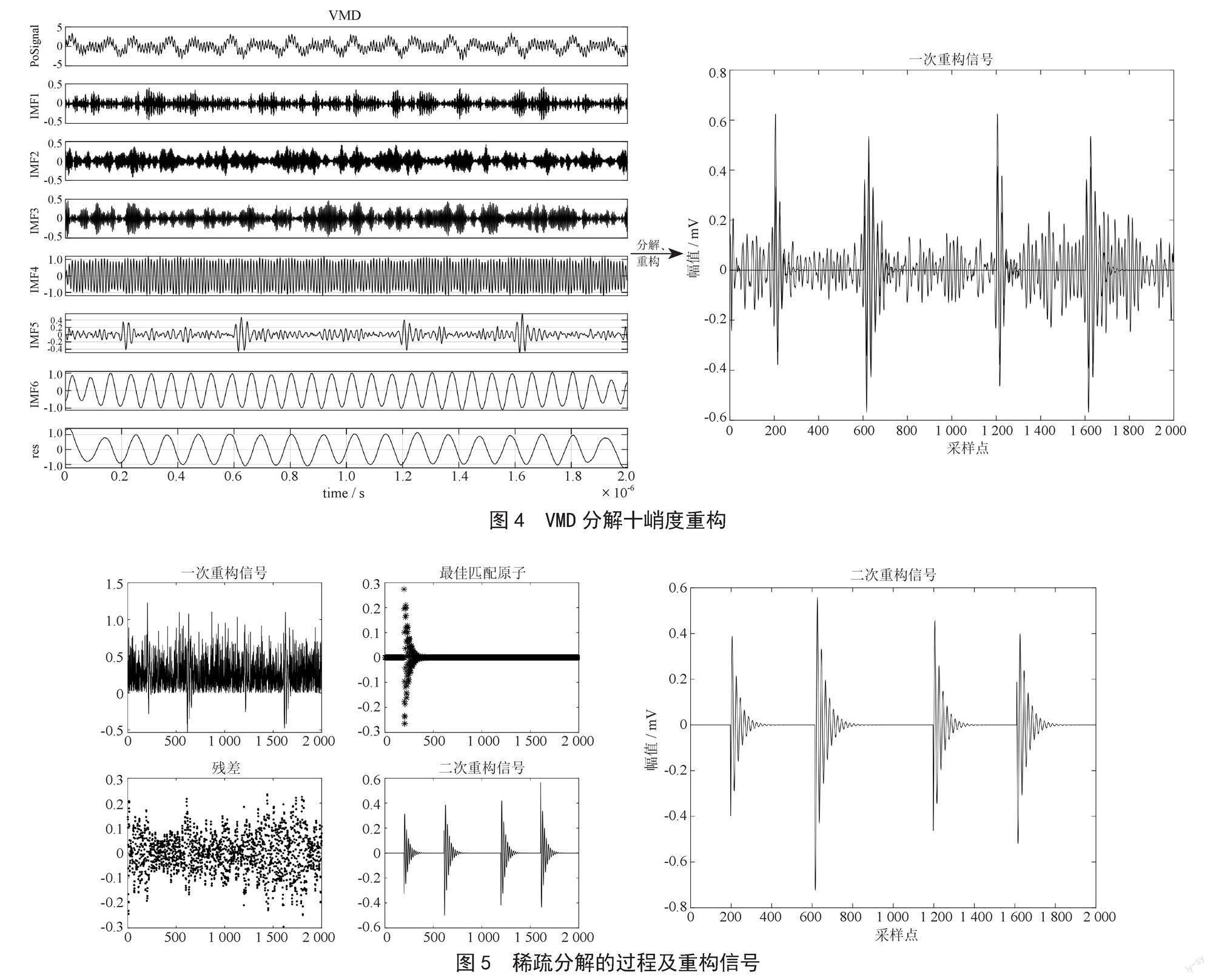
然后，将VMD算法应用于被污染的PD信号。经由VMD分解后的PD信号的不同的模态，计算其每个模态的峭度值，选择前2～3个最大峭度值对信号进行重构，其仿真过程如图4所示。

从图4可以看出经过VMD分解和峭度重构后的PD信号，大部分噪声已经被消除，可以找到其中心频率、带宽以及起始和终止放电点。尽管这些参数可能不够精确，但足以将稀疏分解算法限制在短时间内，而不是整个时域。这种情况下，就可以应用稀疏分解算法来去除PD信号中的剩余噪声。

基于过完备字典和MP算法的稀疏分解过程如图5所示。

信号稀疏分解算法基于在过于完整的字典中找到最佳匹配原子来重构信号。从图5可以看到整个算法的过程，最佳匹配原子在MP贪婪算法的搜索下被笠选出来重构信号，而噪声则被当作残差去除，最后，几乎不含噪声的PD信号被提取出来。

在这种仿真条件下，如果直接使用MP算法而不进行优化，则需要4×2 0003次搜索才能获得最佳匹配原子集合。然而，在算法的作用域自适应性地受到限制后，只需要1×104～2×104次搜索就能获得相同的结果，大大提高了算法的效率。

5  评估与分析

5.1  算法去噪评价

为了比较本文提出的算法的去噪效果相比于传统PD信号去躁算法的效果，本文采用了以下4个评估规则[18]：信噪比（Signal Noise Ratio， SNR）、归一化相关系数（Normalized correlation coefficient， NCC）、降噪率（Noise reduction ratio， NRR）、上升趋势参数（RVTP）和下降趨势参数（FVTP）的平均-VTF。SNR越大，NRR就越大，NCC和VTF越接近1，算法对降噪的影响就越大。

5.2  仿真比较

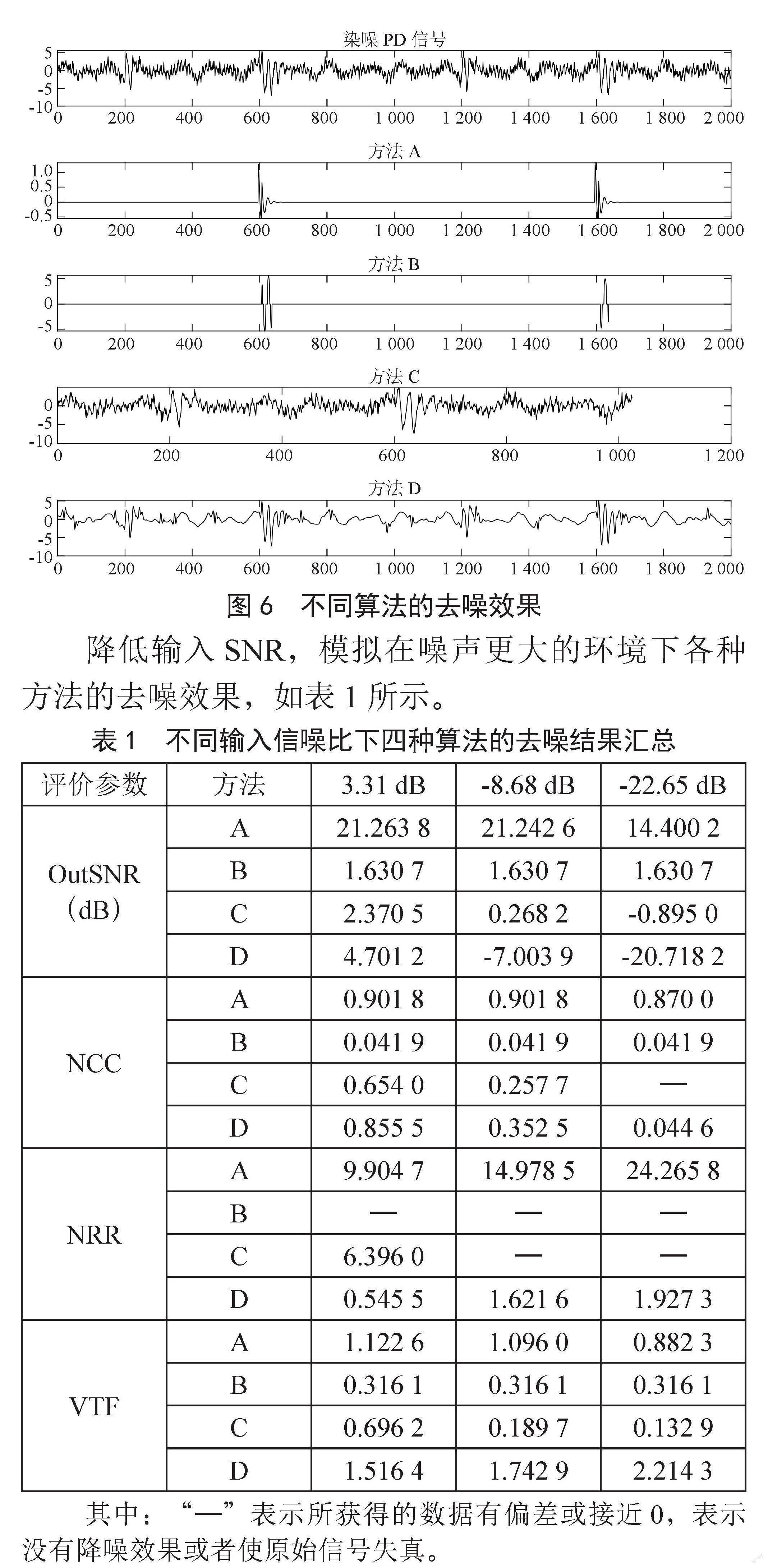
将本文提出的方法（方法A）与其他三种常用的局部放电去噪方法——EEMD（方法B）、SSVD（方法C）和自适应阈值小波（方法D）——对不同输入信噪比的局部放电信号进行作用，比较其降噪效果。例如，当输入SNR为3.79 dB时，可以获得如图6所示的去噪后的结果。

降低输入SNR，模拟在噪声更大的环境下各种方法的去噪效果，如表1所示。

以上结果表明，只有当SNR＞1时，也就是原始PD信号比噪声更明显时，EEMD和SSVD算法才能在PD信号有较好的降噪效果，能提取出原始PD信号。这个结果也可以在其他研究文章中观察到类似的结果[4]。自适应阈值小波方法优于EEMD和SSVD，可以在信噪比较小的情况下使用。然而，当SNR＜-20时，即原始PD信号完全被噪声淹没，这三种传统的PD信号降噪方法基本上没有降噪效果，甚至可能使原始PD信号失真。

而本文提出的方法既可以有效地消除噪声，提取原始PD信号，也可以在低信噪比的条件下依旧保证比较好的去噪效果。

6  实测信号验证与对比

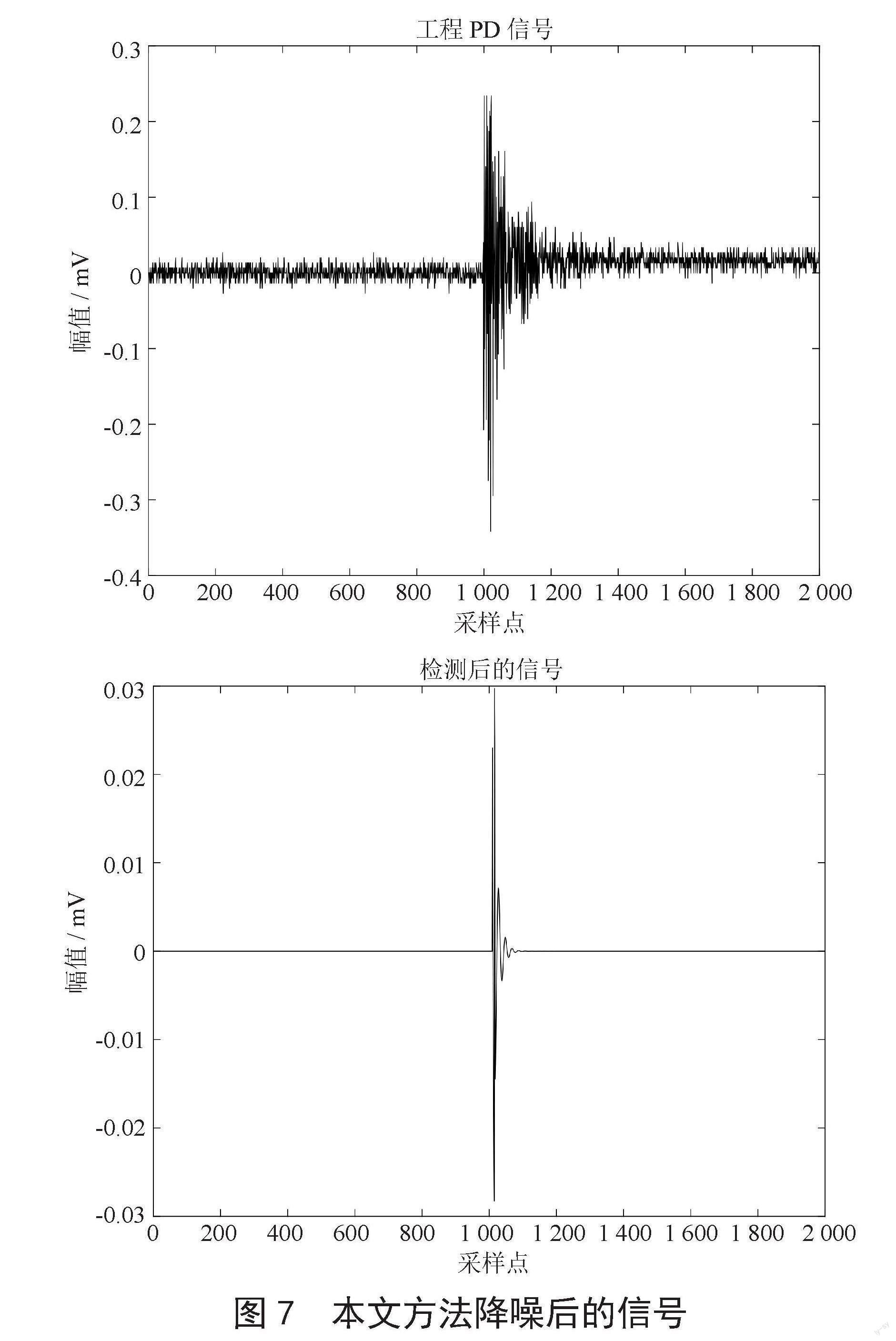
在500 kV高压并联电抗器，传感器为超高频传感器，采样频率为400 MHz的工程环境下检测到的PD信号如下以及运用本文的算法提取后的结果如图7所示。

从上面的结果可以看出，该方法确实精确且自适应地捕捉PD信号的起点和终点，并且对整个信号周期上的噪声进行了去除，并提取出了局部放电脉动。

当将其他传统PD信号去噪算法应用于此工程PD信号去噪时，可以得到如图8所示的结果。

由以上结果可以发现：SSVD算法不能很好地去除噪声，去噪信号的时域中仍然存在一些轻微的噪声；EEMD算法不能定位工程PD信号的精确起点和终点；与其他两种算法相比，硬阈值小波算法产生的结果甚至更差。

总之，本文改进的方法对模拟PD信号和实际工程PD信号都有较好的处理效果。

7  结  论

针对局部放电信号，本文提出了一种自适应VMD和稀疏分解的信号提取方法。为了解决PD信号的过完备字典维度过高、算法效率过低的问题，本文基于VMD算法对稀疏分解算法进行了优化。本文提出的方法不需要设置或选择阈值并可以自适应地限制稀疏分解的作用范围。该方法与其他传统PD信号去噪方法的比较结果，以及将该方法应用于实际工程PD信号的结果共同证明了该方法的有效性和不同信噪比下的适用性。

参考文献：

[1] 李希桐.电力电缆局部放电综合噪声抑制方法的研究 [D].阜新：辽宁工程技术大学，2022.

[2] 饶显杰，徐忠林，龙林，等.基于广义S变换与数学形态学的局部放电窄带干扰抑制方法 [J].电网技术，2023，47（3）：1299-1307.

[3] 李梦莹，邢昕奕，刘雅文.局部放电周期性窄带干扰抑制方法综述 [J].科技创新与应用，2021（1）：142-144.

[4] 付伟，李宁.基于改进EEMD的局部放电信号降噪方法 [J].电子测量技术，2022，45（12）：156-162.

[5] SUN SHENGYA，SUN Y Y，LI Y H，et al. An Adaptive Wavelet Multilevel Soft Threshold Algorithm for Denoising Partial Discharge Signals [C]//2019 IEEE Sustainable Power and Energy Conference （iSPEC）.Beijing：IEEE，2019：1874-1878.

[6] DIAZ-ORTIZ F，ROMAN F. Wavelet denoising using an optimal selection of mother wavelet for compact intracloud discharges [C]//2018 34th International Conference on Lightning Protection （ICLP）.Rzeszow：IEEE，2018：1-4.

[7] ASHTIANI M B，SHAHRTASH S M. Partial discharge de-noising employing adaptive singular value decomposition [J].IEEE Transactions on Dielectrics and Electrical Insulation，2014：775-782.

[8] MANSOURI A，MAHMOUDI-AZNAVEH A. SSVD： Structural SVD-based image quality assessment [J].Signal Processing： Image Communication，2019，74：54-63.

[9] GAO J，WU L F，WANG H M，et al. Development of a Method for Selection of Effective Singular Values in Bearing Fault Signal De-Noising [J/OL].Applied Sciences，2016，6（5）：154[2023-09-16].https：//doi.org/10.3390/app6050154.

[10] 李清泉，王歡.基于稀疏表示理论的优化算法综述 [J].测绘地理信息，2019，44（4）：1-9.

[11] 任倩楠.稀疏表示理论下OFDM信号干扰抑制方法研究 [D].西安：西安理工大学，2021.

[12] SILVA F T A，MOTA H D O. Partial discharge signal processing using overcomplete dictionaries and sparse representations [C]//2017 IEEE Electrical Insulation Conference （EIC）.Baltimore：IEEE，2017：388-391.

[13] 吕宏政，陈仁文，张祥，等.基于VMD交叉样本熵的旋翼桨叶故障诊断方法 [J].电子测量技术，2019，42（9）：107-111.

[14] 佘昌佳，梅飞，叶昱媛，等.基于优化VMD与噪声估计的间隔阈值局部放电去噪方法 [J].高压电器，2020，56（3）：141-149.

[15] HUAI S H，ZHANG S F. A novel sparse representation algorithm for AIS real-time signals [J/OL].EURASIP Journal on Wireless Communications and Networking，2018，223[2023-09-20].https：//doi.org/10.1186/s13638-018-1244-9.

[16] DRAGOMIRETSKIY K，ZOSSO D. Variational Mode Decomposition [J].IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[17] MATHIS H. On the Kurtosis of Digitally Modulated Signals with Timing Offsets [C]//2001 IEEE Third Workshop on Signal Processing Advances in Wireless Communications （SPAWC'01）.Workshop Proceedings （Cat.No.01EX471）.Taiwan：IEEE，2001：86-89.

[18] 唐炬，高丽，彭莉，等.非平稳振荡局放信号去噪效果评价参数研究 [J].高电压技术，2007（12）：66-70.

作者简介：钟俊（1972—），男，漢族，重庆人，副教授，硕士生导师，博士，研究方向：电力系统的信号与信息处理；刘桢羽（1998—），女，汉族，重庆人，硕士研究生在读，研究方向：信号与信息处理等；赵晓坤（1983—），男，汉族，四川广元人，高级工程师，硕士，研究方向：电力信息通信、电力物联网、5G配网保护等领域；唐妮妮（1989—），女，汉族，四川安岳人，副高，硕士，研究领域：电力信息通信、电力物联网、5G配网保护等；通讯作者：毕潇文（1996—），女，汉族，山东淄博人，博士研究生在读，研究方向：信号与信息处理等。