实对称区间矩阵特征值确界的交错定理及其应用
2024-04-13成龙李耀堂
成龙 ,李耀堂
(1.重庆对外经贸学院数学与计算机学院,重庆 401520;2.云南大学数学与统计学院,云南 昆明 650091)
1.引言
在许多科学和工程问题中,由于测量误差、计算误差和数据变化等因素都会导致描述该问题的数学系统中的参数难以精确确定.如何解决不确定参数对系统特性的影响就显得尤为重要.此时,区间分析就发挥了其强大的作用.[1-2]区间分析是考虑在各种因素影响的条件下,给出一个包含真实结果的区间.1966年,MOORE在文[1]中奠定了区间分析的理论基础.随后,区间分析被广泛应用于化学与结构工程、控制电路设计、计算机图形学和行为生态学等领域.[1-3]
在许多实际应用中,由于面对系统的各种不确定因素,系统的雅可比矩阵的元素往往取值于某个实区间中,即系统的雅可比矩阵为区间矩阵,且系统的特性由该区间矩阵的特征值决定.因此区间矩阵特征值界的估计问题吸引了众多学者的关注和研究.[4-21]例如: 1982年,DEIF在文[11]中利用特征值不等式和非线性规划理论,在特征向量分量符号不变的条件下,得到了一类特殊的区间矩阵――实对称区间矩阵特征值的算法;2010年,HLAD´IK等学者在文[15]中给出了实区间矩阵特征值界的估计;2017年,HLAD´IK在文[16]中进一步给出了计算特征向量分量符号不变的实对称三对角区间矩阵各特征值确界的算法.但是,在应用中特征向量分量符号不变的条件往往很难满足,因此这些算法难以应用.另一方面,文[17]中证明了精确计算实对称区间矩阵各特征值的确界是NP-难问题.因此,寻找实对称区间矩阵各特征值界的估计算法具有重要意义.本文将在建立实对称区间矩阵特征值确界的交错定理的基础上,给出实对称三对角区间矩阵各特征值界的估计算法.
2.预备知识
为了叙述方便,本节给出实对称区间矩阵的相关概念和符号,以及与实对称矩阵特征值相关的预备知识.
定义2.1[22]设A=(aij)∈Rm×n,B=(bij)∈Rm×n,对任意的i=1,2,···,m;j=1,2,···,n,若aij ≥0,则记A ≥0;若aij>0,则记A>0;若aij-bij ≥0,则记A ≥B;若aij-bij>0,则记A>B.
1966年,MOORE首次提出区间矩阵的概念,即元素为闭区间的矩阵,其定义如下.
称Ak为A的k阶主子矩阵;称为AI的k阶主子区间矩阵.
定义2.5设AS是实对称区间矩阵,定义AS的k阶主子区间矩阵为
定义2.6[11]设AI是n阶区间矩阵,称AI中所有矩阵的特征值组成的集合为区间矩阵AI的特征值,记为λ(AI),即
一般来讲,n阶区间矩阵AI的特征值λ(AI)是复数域上的一个集合.但对于实对称区间矩阵AS,因为AS中的矩阵都是实对称矩阵,再由实对称矩阵的特征值都是实数知λ(AS)为实数域上的集合.下面讨论λ(AS)在实轴上的分布情况.
在下文中,实对称矩阵A=(aij)n×n的特征值都按升序排列,即
引理2.1[11]若记λi(AS)=则λi(AS)为闭区间,即
注2.1称λi(AS)为实对称区间矩阵AS的第i个特征值区间,简称为AS的第i个特征值;称(AS),λi(AS)分别为AS的第i个特征值的上确界和下确界.
注2.2由引理2.1知实对称区间矩阵AS的特征值由n个闭区间的并集组成,即
由于实对称区间矩阵AS的第i个特征值λi(AS)和第j个特征值λj(AS)(i=j)都为实数轴上的区间,故可能重合,并且精确计算AS各特征值的确界是NP-难问题.[17]本文研究AS各特征值的确界,以便给出AS各特征值界的估计.
为讨论方便,下面先回忆实对称矩阵特征值的交错定理和Weyl 定理.
引理2.2[22](实对称矩阵特征值的交错定理) 设A ∈Rn×n为对称矩阵,Sn-1(A)表示A的所有n-1阶主子矩阵构成的集合,则对任意An-1∈Sn-1(A),有
由引理2.2可直接得到如下推论.
推论2.1[22]设对称矩阵A ∈Rn×n,Sk(A)表示A的所有k阶主子矩阵构成的集合,则对任意Ak ∈Sk(A),有
推论2.1说明实对称矩阵A的所有k阶主子矩阵的最大特征值中的最小者是矩阵A的第k个特征值的上界.
引理2.3[22](实对称矩阵特征值的Weyl定理) 设A,B ∈Rn×n为对称矩阵,则对任意的i ∈N,有
3.实对称区间矩阵特征值确界的交错定理
引理2.2给出了实对称矩阵特征值的交错定理,那么实对称区间矩阵的特征值是否具有类似的结论呢? 下面讨论该问题.
对An-1和A应用引理2.2,有
由(3.2)式、(3.3)式和(3.4)式得
同理可证k=1,2,···,n-2时,有
由(3.7)式、(3.8)式和(3.9)式得
同理可证k=1,2,···,n-2时,有
综上(3.5)式、(3.6)式、(3.10)式和(3.11)式即得(3.1)式.
由定理3.1可得如下推论.
推论3.1设AS是实对称区间矩阵,记Sk(AS)表示AS的所有k阶主子区间矩阵构成的集合,则对任意的∈Sk(AS),有
证当k=1,2,···,n-1时,由定理3.1可得
如此递推,可得如下不等式:
综上即得(3.12)式.
推论3.1表明实对称区间矩阵AS的所有k阶主子区间矩阵的最大特征值的上确界中的最小者是AS的第k个特征值的一个上界.记该上界为(AS),即
定理3.1说明实对称区间矩阵各特征值的上确界具有交错性质.同样的,实对称区间矩阵各特征值的下确界也具有交错性质,即有如下定理3.2,其证明过程类似于定理3.1的证明,略去.
定理3.2(实对称区间矩阵特征值下确界的交错定理) 设AS是实对称区间矩阵,记Sn-1(AS)表示AS的所有n-1阶主子区间矩阵构成的集合,则对任意的∈Sn-1(AS),有
由定理3.2可直接得如下推论.其证明过程类似于推论3.1的证明,略去.
推论3.2设AS是实对称区间矩阵,Sk(AS)表示AS的所有k阶主子区间矩阵构成的集合,则对任意的∈Sk(AS),有
推论3.2说明实对称区间矩阵AS的所有n+1-k阶主子区间矩阵的最小特征值的下确界中的最大者是AS的第k个特征值的一个下界.记该下界为(AS),即
4.实对称三对角区间矩阵特征值界的估计
实对称三对角区间矩阵是一类特殊的实对称区间矩阵,通常由微分方程的有限元和有限差分离散化产生,例如:离散多质点弹簧系统的刚度矩阵等.在文[14]中,YUAN证明了实对称三对角区间矩阵的最大和最小特征值的上、下确界等价求4个实对称三对角矩阵的极值特征值.在文[16]中,HLAD´IK在区间矩阵的特征向量分量符号不变的条件下,给出了计算实对称三对角区间矩阵特征值确界的算法.但实对称三对角区间矩阵的特征向量的分量符号不变这个条件太强,往往难以满足,参见下文中的例5.2.这就要求我们进一步研究,探讨可以估计任意实对称三对角区间矩阵各特征值界的方法,即给出计算实对称三对角区间矩阵各特征值的外近似区间(即包含特征值的闭区间)的新算法.
本节应用上节所获实对称区间矩阵特征值确界的交错定理构造实对称三对角区间矩阵TS各特征值上界和下界的估计式,最后给出计算TS各特征值外近似区间的算法.
定义4.1[14]设区间矩阵称TS为实对称三对角区间矩阵,其中Tc,T∆分别为TS的中点矩阵和半径矩阵.显然,对于任意的T ∈TS,T具有以下形式:
在文[14]中,YUAN证明了实对称三对角区间矩阵TS的最大特征值的上确界等于TS中的如下矩阵U的最大特征值,即有如下引理4.1.
引理4.1[14]设TS是形如(4.1)式的实对称三对角区间矩阵,令
证首先证明-TS是实对称三对角区间矩阵.因为TS是实区间矩阵,由区间矩阵的定义知,-TS也是实区间矩阵;设T是TS中任意的对称三对角矩阵,则-T ∈-TS,又-T也是实对称三对角矩阵,所以-TS是实对称三对角区间矩阵.
现在证明TS和-TS的特征值的确界满足(4.2)式,即需证明
设实对称三对角矩阵T和-T的特征值分别为:
由矩阵特征值的定义知,T和-T的特征值满足
由引理2.1知,对任意的i ∈N,存在T ∈TS,满足
又由(4.4)式知
由(4.5)式和(4.6)式即得(4.3)式.
注4.2定理4.1说明TS的第i个特征值的下确界(下界)可以通过求-TS的第n+1-i个特征值的上确界(上界)的相反数给出,所以本文只给出计算TS各特征值上界的估计式.
由引理4.1和推论3.1可以给出估计实对称三对角区间矩阵各特征值上界的方法,即有如下定理4.2.
定理4.2设TS是形如(4.1)式的实对称三对角区间矩阵,则对任意的k ∈N,
是TS的第k个特征值λk(TS)的一个上界,且
定理4.3设TS是形如(4.1)式的实对称三对角区间矩阵,则对任意的k ∈N,有
其中Tc,T∆分别为TS的中点矩阵和半径矩阵,j=0,1,···,n-k,Sn-j(T∆)表示矩阵T∆的所有n-j阶主子矩阵构成的集合.
证由实对称三对角区间矩阵TS可表示为TS=[Tc-T∆,Tc+T∆]知,任意的T ∈TS可表示为T=Tc+δT,其中δT ∈[-T∆,T∆]为实对称矩阵.由引理2.3知,对任意的k ∈N有
其中j=0,···,n-k.再由定理4.2得
由(4.8)式和(4.9)式即得(4.7)式.
由引理4.2知,TS与TS的子集合TD={T ∈TS|aii=∀i ∈N}的各特征值有相同的上界.由于TD仍是实对称三对角区间矩阵,将定理4.3的结论应用于TD可以得到TS各特征值上界的估计,即有下面的定理4.4.
Tc,T∆分别是TS的中点矩阵和半径矩阵,j=0,1,···,n-k,Sn-j(T∆-D)表示矩阵T∆-D的所有n-j阶主子矩阵构成的集合.
由于定理4.2-4.4都是实对称三对角区间矩阵TS各特征值上界的估计式.下面将三个定理的结果取最小者作为实对称三对角区间矩阵TS各特征值的上界,给出计算TS各特征值外近似区间的如下算法.
算法4.1
5.数值例子
本节应用本文的定理4.2-4.4和算法4.1,计算两个实对称三对角区间矩阵各特征值的外近似区间,并与几个现有算法进行比较.在表1和表2中,P1、P2、P3和P分别表示利用定理4.2-4.4和算法4.1得到实对称三对角区间矩阵各特征值的外近似区间;Q表示HLAD´IK等学者在文[15]中给出的实对称区间矩阵各特征值的外近似区间;M表示HLAD´IK在文[16]中给出的实对称三对角区间矩阵各特征值的近似区间.
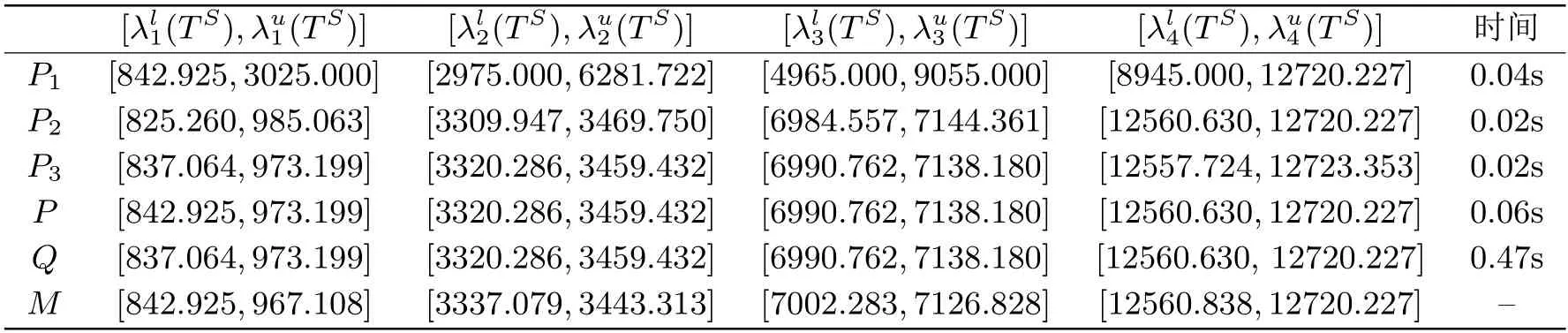
表1 实对称三对角区间矩阵TS各特征值的近似区间

表2 实对称三对角区间矩阵KS各特征值的近似区间
例5.1求如图1中具有单位质量和区间刚度的离散四质点弹簧系统的刚度矩阵各特征值界的估计.其中各弹簧的刚度系数分别为k1=1000±10N/m;k2=2000±15N/m;k3=3000±20N/m;k4=4000±25N/m;k5=5000±30N/m.
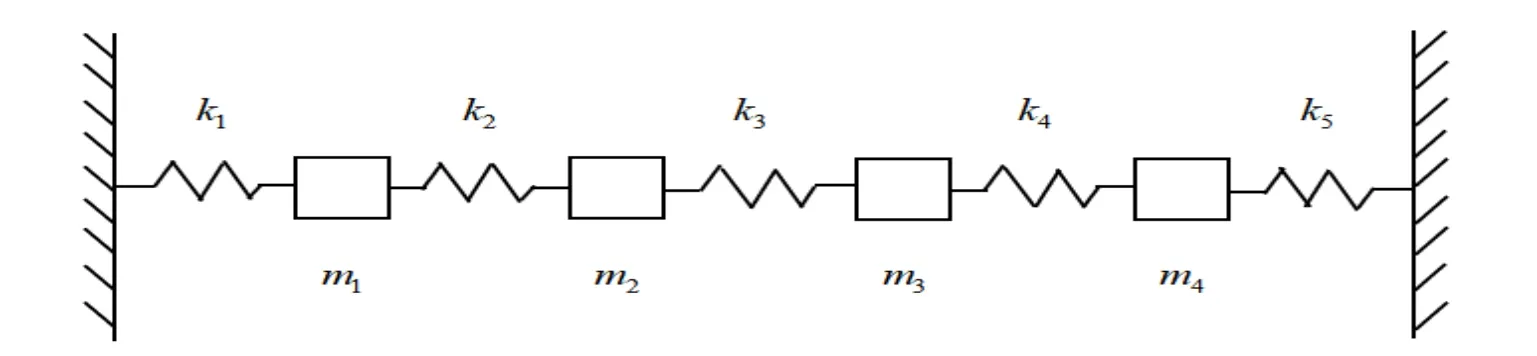
图1 四质点弹簧系统
根据离散多质点弹簧系统的刚度矩阵与刚度系数之间的关系可得到该弹簧系统的区间刚度矩阵为
一方面,对比表1中P与Q的数据,不难发现利用算法4.1得到TS各特征值的外近似区间更小,运行时间也更少.另一方面,由于该例子的特殊性,TS的特征向量分量符号保持不变,故可用文[16]中的算法进行计算,M中给出TS各特征值的近似区间就等于TS的各特征值区间,再对比P中的数据,可以观察到利用算法4.1得到TS各特征值的外近似区间与TS的各特征值区间差距不大,并且不用去验证TS是否满足先验条件,计算成本也更小.观察P1、P2、P3中的数据还可以发现,当实对称三对角区间矩阵各特征值区间重叠较少或不重叠时,利用定理4.3和定理4.4进行特征值区间的估计,结果较为理想;而利用定理4.2进行特征值区间的估计,结果并不理想.
例5.2计算实对称三对角区间矩阵KS各特征值的界,其中
对比表2中P与Q的结果,可以发现利用算法4.1得到KS各特征值的外近似区间更小,运行时间也更少.又因为KS不满足文[16]中所给算法的适用条件,所以不能给出KS各特征值的外近似区间.而本文给出的算法4.1能够更好的获得任意实对称三对角区间矩阵各特征值的外近似区间.观察P1、P2、P3中的数据还可以发现,当实对称三对角区间矩阵各特征值区间重叠较多时,利用定理4.2进行特征值区间的估计,结果较为理想;而利用定理4.3和定理4.4进行特征值区间的估计,结果并不理想.
以上两个例子表明,由于算法4.1是将三个定理的结果取最小者作为实对称三对角区间矩阵各特征值的上界,故本文的算法克服了实对称三对角区间矩阵各特征值区间重叠情况对估计结果的影响,所以本文算法能够较好的估计任意实对称三对角区间矩阵的各特征值区间.
6.总结
本文将实对称矩阵特征值的交错定理推广到实对称区间矩阵,给出了实对称区间矩阵特征值确界的交错定理,并应用其给出了计算实对称三对角区间矩阵特征值界的新算法.文中数值例子表明,与一些现有算法相比,本文算法适用于所有的实对称三对角区间矩阵,得到的界较为精确,计算成本也更加小.
