一种整数线性乘积规划问题的分支定界算法
2024-04-13李敏敏高岳林
李敏敏 ,高岳林
(1.北方民族大学数学与信息科学学院,宁夏 银川 750021;2.宁夏科学计算与智能信息处理协同创新中心,宁夏 银川 750021)
1.引言
整数规划可用于解决众多领域中的实际问题,如工商管理、工程技术、金融及社会科学等.随着科学技术的发展和决策问题求解的迫切需要,非线性整数规划问题的算法研究已经成为运筹学与最优化领域的研究热点之一.[1-2]求解非线性整数规划问题的确定性方法有割平面法[3]、分解算法[4]、外逼近法[5]、分支定界法[6-10]等.由于整数规划是NP难问题,现有算法仅可以求解某种特殊形式的整数规划问题,且往往存在收敛速度慢、最优解效果差、计算复杂等不足,对于特殊的非线性整数规划问题――整数线性乘积规划问题,至今还没有一个通用而有效的算法.本文主要考虑以下形式的整数线性乘积规划问题:
这里αj>0,cj ∈Rn,dj ∈R,j=1,···,p.A ∈Rm×n,b ∈Rm,假定+dj ≥ε>0,j=1,···,p.X0为非空有界闭集.
(ILMP)不仅应用于金融优化[11]、证券投资[12]、微观经济学[13]等金融经济问题中,而且在VLISI芯片设计[14]、数据挖掘[15]、鲁棒优化[16]等方面也有涉及.由于(ILMP)问题是一个NP-hard问题[17],且往往存在许多局部最优解而不是全局最优解,这就使得在理论和计算上存在巨大的挑战.因此,寻找一种有效的算法全局求解(ILMP)问题是十分必要的.
从(ILMP)问题的研究历程来看,已经有许多算法都适用于求解全局(LMP)问题,求解全局(ILMP)问题的算法相对较少,现如今分支定界算法已成为求解这类问题最常用的工具之一.根据分支定界算法的框架,基于对(ILMP)问题的松弛,在每个节点求解松弛子问题的下界,得到一个高质量的下界对原问题起着至关重要的作用.SHAO和Ehrgott[18]提出了利用多目标线性规划和原始对偶条件求解(LMP)问题的全局优化算法.对于广义线性乘积规划问题,JIAO[19]利用指数函数和对数函数的线性逼近,建立了一类广义线性乘法规划的可靠高效算法.SHEN[20]将适当删除技术与分支定界格式相结合,提出了求解广义线性乘法规划的一种新的加速方法.针对指数型线性乘法规划问题,LIU和ZHAO[21]在Youness[22]的研究基础上提出了一个水平集算法.SHEN等人[23]提出了一个完全多项式时间逼近算法.对于约束中具有线性乘积项的问题,Benson[24]提出了一种基于分解的分支定界算法,Kuno[25]提出了一种基于Soland矩形分支定界法最小化多面体上仿射函数乘积的算法.
非凸(ILMP)问题的困难源于决策变量的非连续性以及目标函数为线性乘积,松弛过程中需要将目标函数的连乘利用对数恒等式进行转换以及将决策变量松弛为连续变量,本文给出了求解整数线性乘积规划(ILMP)问题的全局优化算法.该算法结合分支定界操作和区域缩减技术,通过利用对数函数的恒等式,将目标函数等价转化为对数函数求和的形式,使用线性松弛技术将非凸(ILMP)问题转化为线性松弛规划问题,并将其嵌入到分支定界操作中.为了加快算法的收敛速度,在分支和定界过程中采用了区域缩减技术,为当前不存在全局最优解的区域提供了理论可能性,可以显著减少松弛间隙.结合新的线性化技术、分支定界操作、区域缩减技术,本文提出了一种简化的分支定界区域缩减算法.最后,数值实验结果表明,该方法能较好地解决所有存在于全局最优解中的(ILMP)问题.
本文的组成结构如下: 第一部分提出了整数线性乘积规划问题,并且概述了求解整数线性乘积规划问题的相关算法.第二部分描述了怎样将问题(ILMP)转化为一个等价的问题(EILMP(Hk)).第三部分利用对数函数的单调性和凹凸性得到(ILMP)的松弛问题.第四部分将第三部分得到的线性松弛规划,以及区域缩减技术嵌套在分支定界框架内,得到线性松弛分支定界算法以求解整数线性乘积规划问题.第五部分通过实例证明算法的有效性和可行性.第六部分得出相关结论.
2.等价问题
为了以下叙述的方便,我们首先介绍两个常用的取整函数,分别是上取整函数和下取整函数.上取整函数在数学中记作「r⏋,表示不小于r的整数中最小的一个;下取整函数在数学中记作「r」,表示不超过r的整数中最大的一个.即:
本节将分两个阶段对问题(ILMP)进行等价转换.
第一个阶段:记问题(ILMP)的可行域为X=X0∩Zn,构造包含X的整超矩形H=[l,u]={x|l ≤x ≤u,l,u ∈Zn},其中
这里ai,bi分别是(2.1),(2.2)的最优值,当i ∈{1,2,···,n}时,
因此,我们得到问题(ILMP)在Hk上的第一个等价问题如下:
第二个阶段: 根据对数恒等式以及对数函数的性质可得:
根据指数函数的单调性,问题(ILMP)可被再次改写为以下问题:
3.定界技术
我们将利用对数函数fj(y)=ln(yj)的凹凸性给出问题(ILMP)在超矩形上的下界函数hj(y)为:
定理3.1对于任意的y ∈V k,考虑fj(y)和hj(y)有下列两条性质:
1) 函数hj(y)是函数fj(y)的凸包,另外fj(y)和hj(y)满足:
2)fj(y)和hj(y)之间的差值满足:
其中,∆j(y)=fj(y)-hj(y).
2) 记Θj(yj)=∆j(y),我们有:
根据定理3.1,问题(EILMP(Hk))可被松弛为:
注2Ωk中的点x∗也不一定满足x∗∈X0,所以在算法中需要判断这些解的可行性.
4.分支定界算法及其理论分析
Ⅰ 整超矩形的分支规则
为了得到原问题(ILMP)的全局最优解,提出了整超矩形分支定界算法.在H0被剖分后的子集上求解一系列线性松弛规划问题.在分支过程中,需要依据一定的剖分规则将初始超矩形H0分成两个新的子矩形.本文所采用的是标准整超矩形二分方法.考虑任一通过Hk=[lk,uk]所确定的子节点问题.分支规则如下所示:
通过以上分支规则,将矩形区域Hk剖分成两个子矩形Hk1和Hk2.
为了方便起见,把H0的任意子整超矩形都记作Hk,记LBk是线性松弛规划问题(LRP(Hk))的最优值,xk是相对应的最优解.
Ⅱ 整超矩形的缩减规则
结合矩形分支规则和缩减规则,设计了以下求解问题(ILMP)的分支定界算法,步骤如下:
步1 (初始化)
步1.1 构造关于x的初始整超矩形H0=[l0,u0],置可行解集合W=∅.
步1.2(初始下界) 求解问题(LRP(H0)),置初始下界L0=min{Fl(x,y):x ∈H0},对应最优解为(x0,y0).
步1.4 置容忍度ε>0,迭代次数k=0;超矩形集合Q=∅.
步2 (迭代过程)
步2.1(终止条件) 若Uk-Lk<ε,且(xk,yk)是问题(EILMP)的可行解,则迭代终止.输出问题(EILMP)的全局最优解(x∗,y∗)=(xk,yk),然后将x∗代入原问题(ILMP)的目标函数求得最优值f(x∗).否则令剖分产生的超矩形集合Q=Q∪{H0};转置步2.2.
步2.2(超矩形选择) 置Hk=min{L(H)|H ∈Q}.
步2.4(超矩形缩减) 运用前面给的整超矩形的缩减规则,对剖分后的子超矩形进行缩减,为了方便起见,把缩减后产生的新的超矩形仍然记为Hkj,(j∈{1,2}).
步2.5(子问题求解)求解问题(LRP(Hkj)),置Lkj=min{Fl(x,y) :x ∈Xk∩Hkj},对应最优解为(xkj,ykj)(j ∈{1,2}).
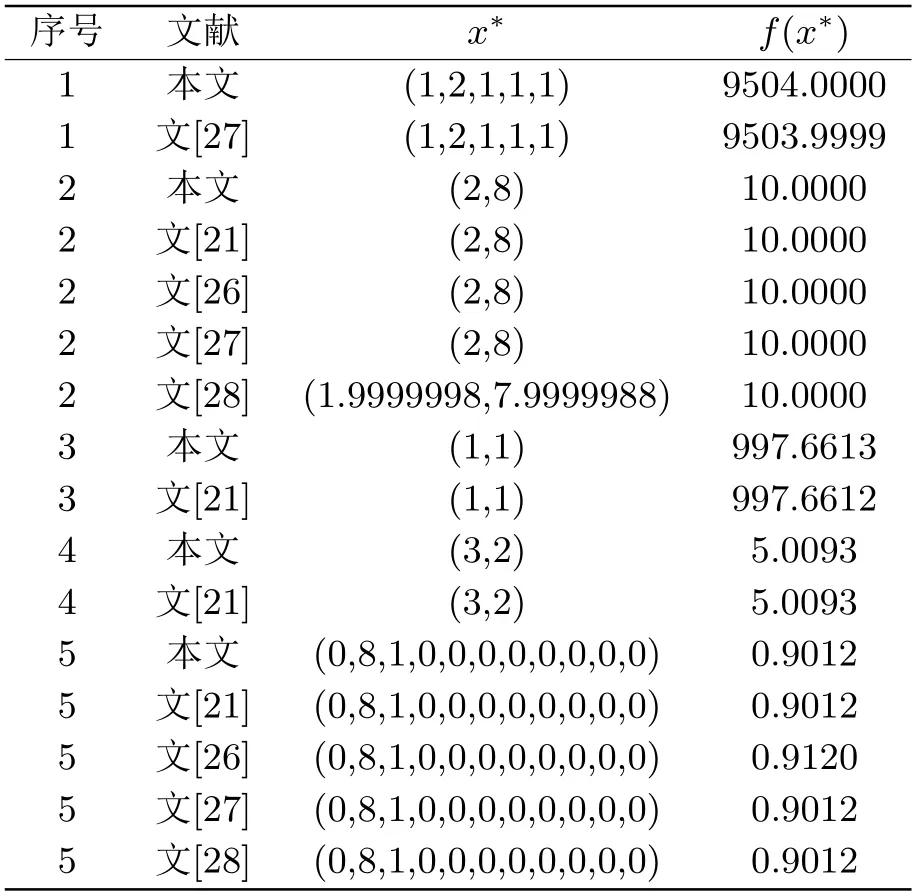
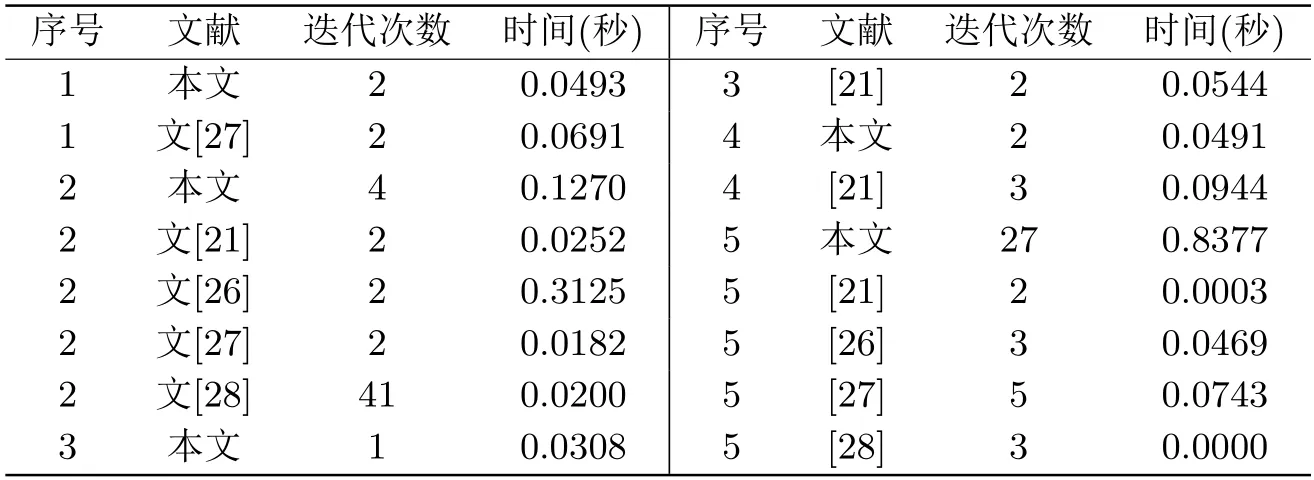
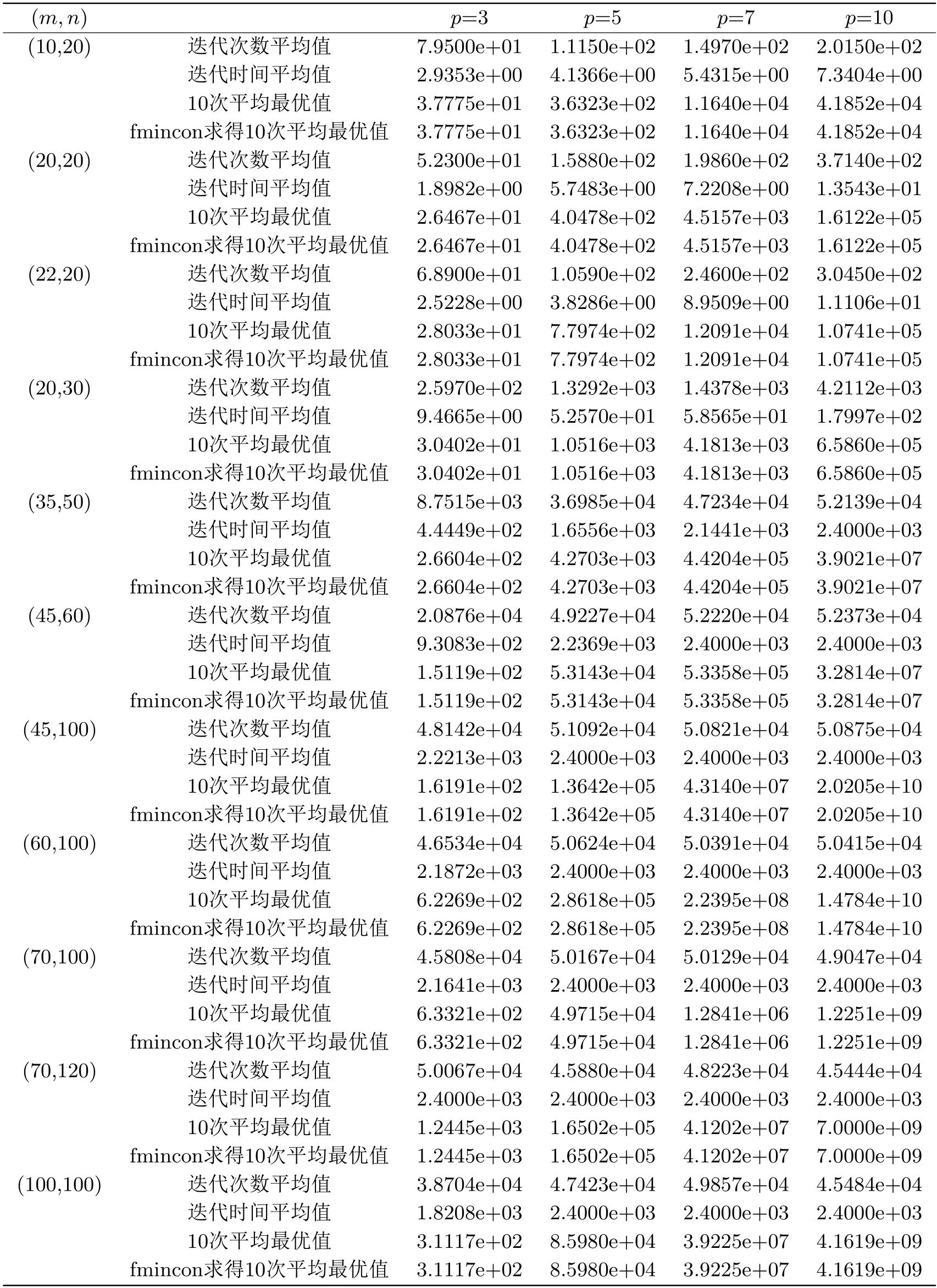
步2.7(超矩形删除) 若L(Hkj) 步2.8(更新上下界) 步2.8.1(更新上界) 置Uk=min{Uk,min{F(x,y): (x,y)∈W}},若Uk=min{F(x,y):(x,y)∈W},则当前最优解(x∗,y∗)=argmin{F(x,y) : (x,y)∈W}.其中x∗为原问题(ILMP)的最优解. 步2.8.2(更新下界) 置Lk=min{L(H):H ∈Q},置k=k+1,转置步2. 证假设(xk,yk)是问题(LRP(xk,yk))的ε-全局最优解,这里yj=+dj,j=1,2,···,p.如果(xk,yk)是(EILMP(xk,yk))的可行解,根据U和L(Hk)的定义知 定理4.1证毕. 定理4.2假设(EILMP)问题的可行域是非空的,且矩形的剖分是耗尽的,则以下结论成立: (EILMP)问题的全局最优解将在算法迭代有限步终止时得到. 证因为本文研究的是整数规划问题,故算法迭代在有限步终止,假设算法是在第k次迭代终止,k ≥0.根据算法的步1和步2.1得到Uk-Lk ≤ε.由步1和步2.8.1可知,等价问题(EILMP)存在可行解(x∗,y∗)使得Uk=F(x∗,y∗),因此有 假设v是等价问题(EILMP)的全局最优值,由下界的计算过程表明 由于(x∗,y∗)是等价问题(EILMP)的可行解,有 联立式(4.3)-(4.5)得 所以,(x∗,y∗)是等价问题(EILMP)的全局最优解. 定理4.2保证了当∥l-u∥→0时线性松弛规划问题(LRP(Hk))无限地逼近于等价问题(EILMP),说明本文给出的分支定界算法是全局收敛的. 以下给出几个例子证明本文算法的有效性.本文算法中所有的线性规划问题均选用对偶单纯形法求解,算法所有测试过程均用MATLAB9.2.0.538062 (R2017a)在Inter(R)Core(TM)i5-8250U,CPU@1.60GHz,4GB内存,64位Windows10操作系统的计算机上运行. 算例1[27] 通过本文的算法将算例1转化为以下等价问题(EILMP): 其中H1=[1,1,1,1,1;1,2,1,1,2]T,V1=[18,6,2,10;21,12,8,13]T,图1中的○1处的矩形为H1, 图1 分支流程图 下面构造线性规划松弛问题(LRP): 解线性规划问题(LRP),得出问题在第一个矩形H1上的下界8.9206,在第一个矩形H1上得到上界对应的最优解x1=[1;2;1;1;1],最优值9.1595;再选择下界对应的矩形H1作为下次剖分的矩形,通过本文的剖分规则得到矩形H11=[1,1,1,1,1;1,1,1,1,2]T,H12=[1,2,1,1,1;1,2,1,1,2]T,图1中的○2处的矩阵为H11,○4处的矩阵为H12;对H11进行缩减,在H11上计算的下界为9.2183,大于当前上界9.1595,H11被删除,此时在图1中对应的位置是○3,对H12进行缩减,在H11上计算的下界为9.1595,H12被删除,这样超矩形的集合T为空,松弛问题的目标值为9.1595,全局最优值为9.1595,最优解为x1=[1;2;1;1;1],具体迭代过程如图1. 算例2[21,26-28] 算例3[21] 算例4[21] 算例5[21,26-28] 根据文[28],我们可知算例5可被改写为: 算例6 算例1-5的计算结果如表5.1所示,算法运行过程中的精度为10-4,得到最优值f(x∗)和最优解x∗.表5.2表示每个算例使用不同的算法得到的平均迭代次数(Iteration(次))和平均运行时间(Time(s)).利用文[21,26-28]中的算法和本文算法进行比较,从总体看本文算法在5个算例上取得的最优值和最优解与其他算法的相同,证明了本文算法的有效性.从计算效果看,本文算法在算例1,算例3和算例4中无论是平均迭代次数还是平均运行时间上均取得了不错的效果,在算例2中本文算法的运行效果与其他算法相比相差不大.在算例5中本文算法无论是在平均迭代次数还是平均运行时间方面与其他算法相比较差.从总体看5个算例的数值结果证明了我们提出的算法是可行并且有效的. 表5.1 算例1-5利用本文算法产生的数值结果 表5.2 算例1-5 利用本文算法产生的数值结果 为了进一步证明我们的算法是有效的,对算例6进行了随机试验,计算结果呈现在表5.3和5.4中,下文也做出了相应的说明. 表5.3 算例6利用本文算法产生的数值结果 由于目前求解整数规划的分支定界算法较少,本文通过Matlab自带的求解非线性规划的求解器fmincon来对比最优值进而证明算法的可行性,另外由于求解器无法求解整数规划问题,特在约束条件中加入x(1-x)=0的等式约束,确保求得的解为整数解.因此使用求解器fmincon和我们的算法对算例6同时进行计算,并将结果置于表5.3和5.4中,表中m表示约束条件的个数,n表示目标函数的维数,p表示目标函数中线性乘积项的个数,在表5.3中,在m和p不变n逐渐增大的情况下,m较小时,迭代次数与迭代时间明显增加,m较大时,迭代次数与迭代时间均无明显变化;当n和p固定,m不断增加时,迭代次数与迭代时间均无明显变化.而且,随着p的增加,迭代次数和迭代时间在m和n越小时趋于不变.另外,本文算法求得的最优值与求解器fmincon求得的完全相同,故表明我们的算法是有效的.在表5.4中,在m和n不变p逐渐增大的情况下,迭代次数和迭代时间基本保持不变. 表5.4 算例6利用本文算法产生的数值结果 针对一般的整数线性乘积规划问题,本文基于对数函数的性质和单调性求解关于整数乘积的线性松弛问题.为了加速算法的收敛性,利用对数函数的性质和单调性进行松弛,以及结合区域缩减技术,通过剖分矩形区域并解决线性子问题,提出的算法最终收敛到原问题(ILMP)的全局最优解.在第五节数值实验中,证实了在求解(ILMP)问题时本文算法是有效并且可行的.5.数值实验


6.结论
