系统思辨 整体架构
——“大单元”理念下“分数初步认识”单元教学的实践与思考
2024-04-12浙江绍兴市上虞区盖北镇小学312369顾婷婷
浙江绍兴市上虞区盖北镇小学 (312369) 顾婷婷
浙江绍兴市教育教学研究院 (312099) 徐雪刚
●争鸣:分数认识何处始?
关于“分数初步认识”一课的教学,可谓百家争鸣,不同专家有不同的观点:或从“量”切入,或从“率”开启,都试图让学生更高效地认识和理解分数。特级教师朱国荣老师指出:“一开始就把分数教成一个量与另一个量的关系,不是一种合理的教学顺序,这是学生难以理解和接受的根源。”特级教师俞正强老师教学时是从“量”的认识开始,再到“率”的体悟,最后对两者进行辨析。而刘善娜老师则质疑:“教材和配套练习中均是以‘率’为主。如果三年级只教学‘量’,后续分数的教学如何处理?”
●思辨:教学实践何所依?
研读教材,把握本质,是有效开展单元整合的前提。整合教材并不是盲目地改编教材,而是要在充分尊重教材的基础上,抓住数学知识的本质和知识发展的主线。研读教材不仅仅是针对某一节课的教材,还应从单元的角度、从整个小学数学教材的角度进行研读,甚至可以从“同一知识体系”中小学教材的编排角度进行研读,以理解教材的编排脉络,全面把握教材的内容编排。为此,笔者对人教版教材中分数的相关内容进行了详细的梳理,并进行了全面的学情分析。
一、读教材——先“率”后“量”,“理想”“现实”有冲突
三年级上册的教材,是从“一个物体为整体”过渡到“多个物体为整体”,让学生逐步加深对分数所表达的“部分—整体”关系的认识。“分数初步认识”这一单元内容全都围绕“率”这一基本含义展开(见表1)。
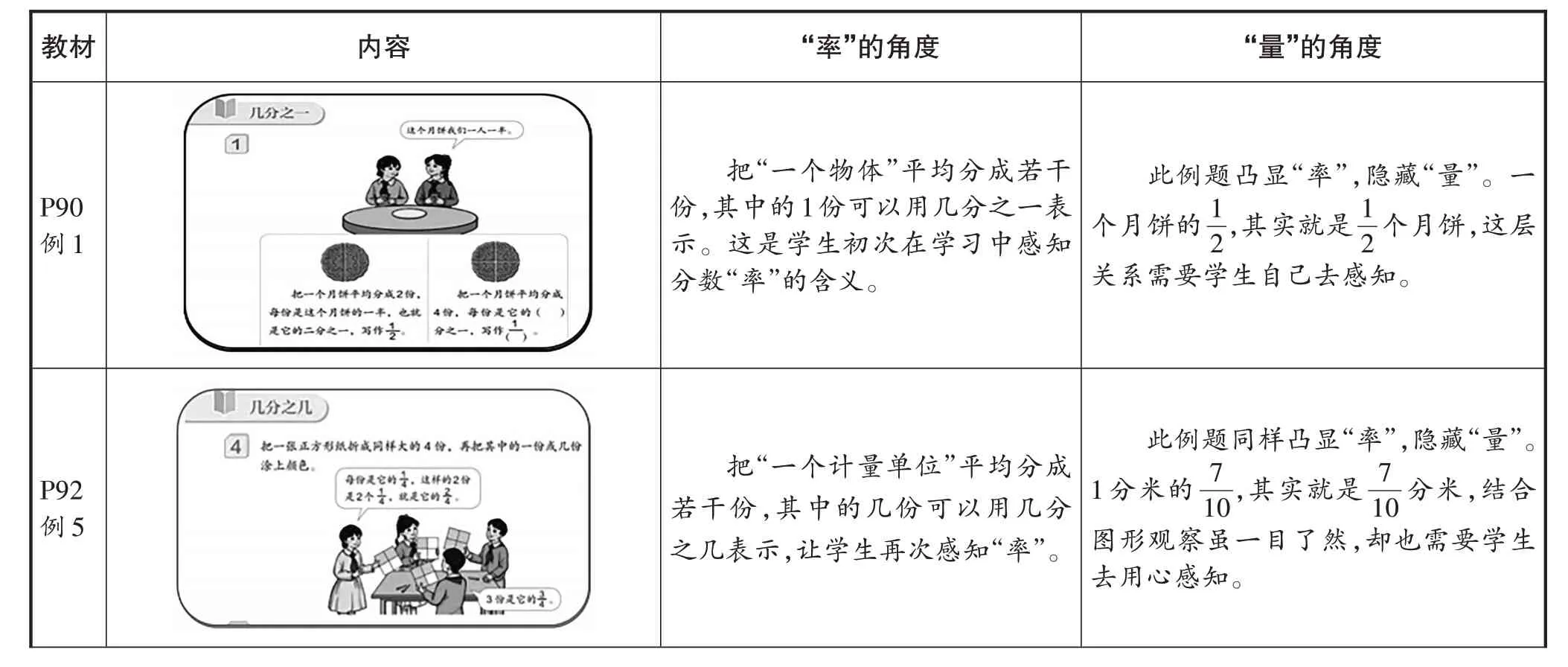
表1 三年级上册“分数的初步认识”单元教材分析
虽然这样的编排充分考虑到了分数概念的抽象性及其理解方式的多样性,但是还存在以下几个问题。
(一)“学科”“学生”有冲突
考虑到“部分—整体”概念在分数中所处的地位,教材是让学生先从重要的内容入手,因为这样可以按照学科知识逻辑的顺序进行教学。然而,小学生从一年级入学开始,接触的数基本是“量”而非“率”,只有在三年级上册“倍的认识”中,学生“临时”接触了一下“比率”。因此,在初步认识分数时,如果教师没有明确解释,学生对分数的第一印象会是“量”,还是“率”,抑或模糊不清?
(二)“相关教学”难衔接

表2 三年级下册“小数的初步认识”中涉及“分数”的内容
(三)“配套练习”有纠结
教材编排的习题(如图1-1、1-2)原意是想体现分数的“率”,但又没有点明,这样难免引起学生的误解,造成学生混淆“量”“率”,因为如果要真正体现含义是“率”的分数,如图1-3、1-4 所示的习题更合适。

图1-1
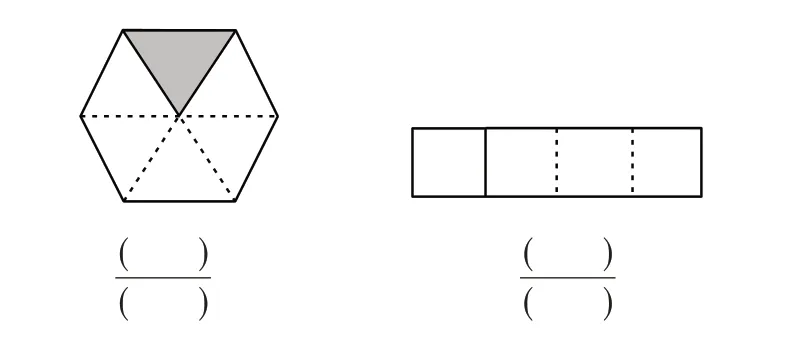
图1-2
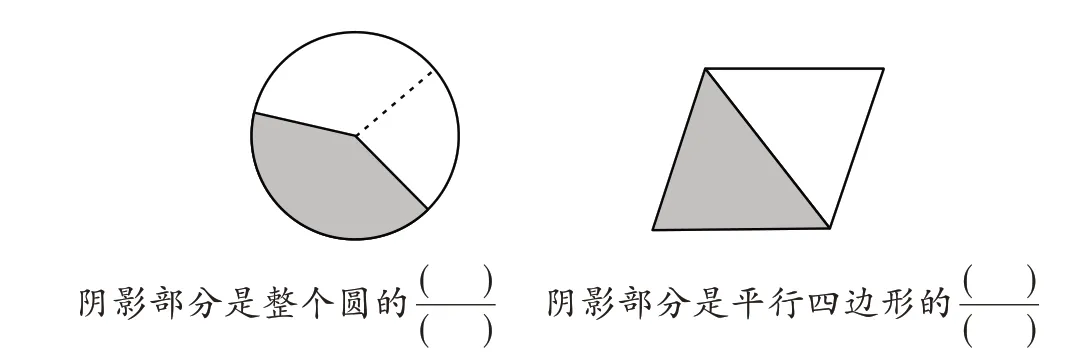
图1-3
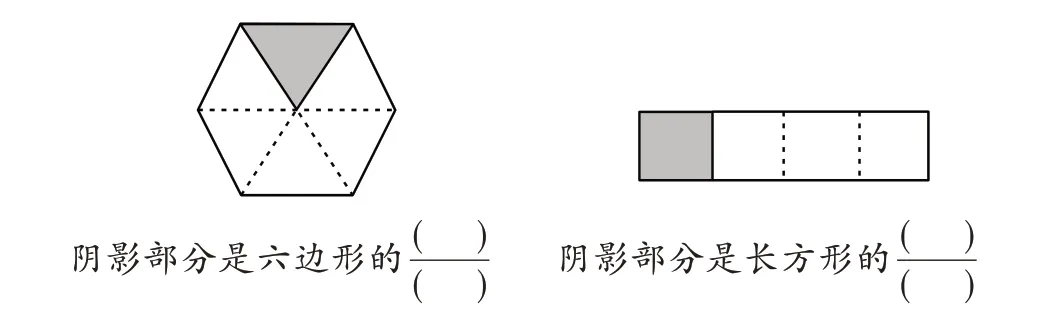
图1-4
配套的课堂作业本在“分数的初步认识”这一单元中多次出现“量”的习题(如图2-1、2-2)。教材和教学目标都未体现“量”,为何配套的课堂作业本中频繁出现“量”的习题?

图2-1

图2-2
(四)后续学习存“痛点”
五年级下册“分数的意义”在单位“1”中呈现分数“率”的含义(见表3)。“分数与除法”是教材首次出现“量”,但后续直接呈现“量”“率”结合的题目,学生还来不及辨别“量”“率”的差异,“量”旋踵即逝,这样的编排是否会给学生的后续学习留下“痛点”?
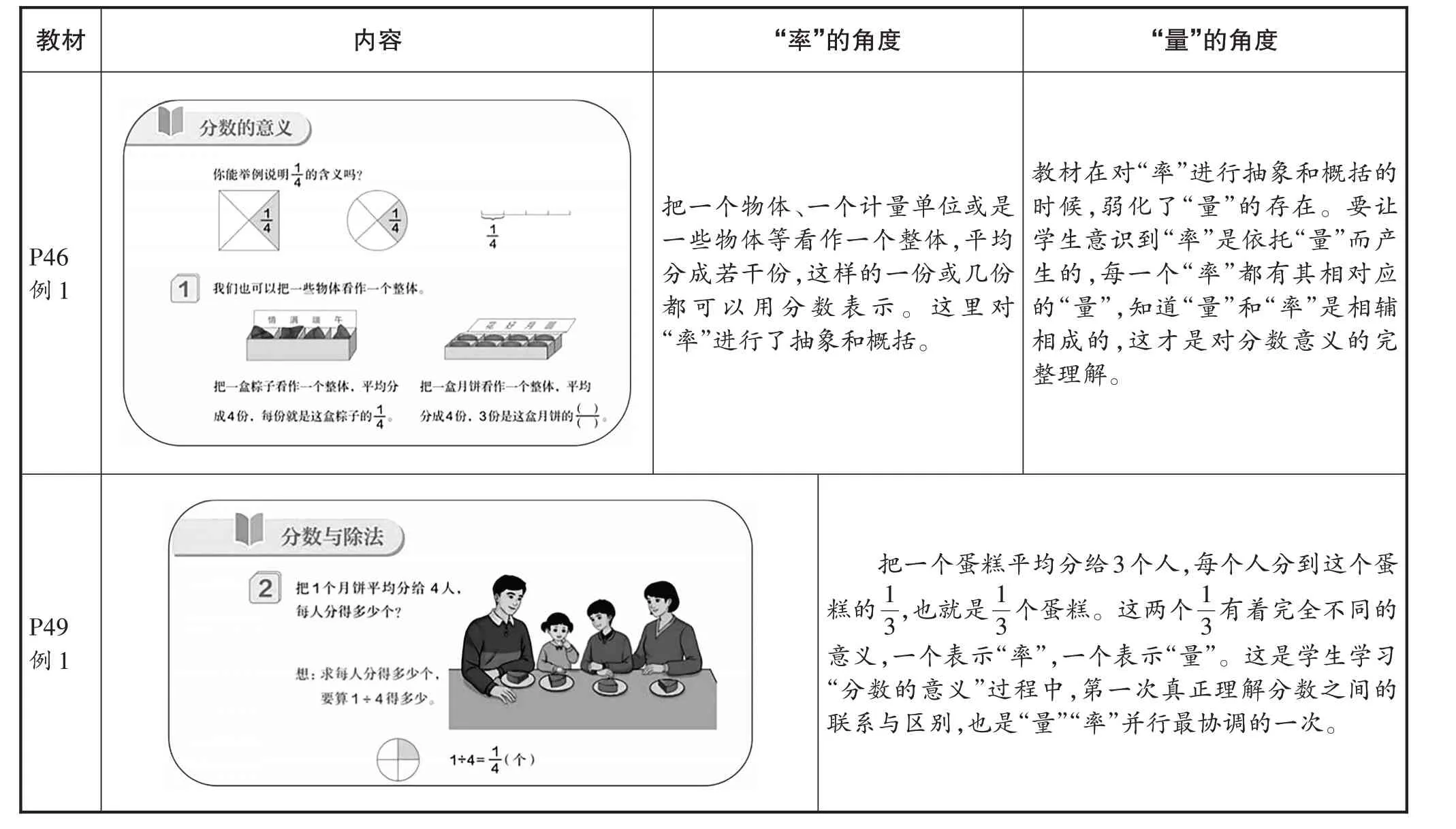
表3 五年级下册“分数的意义”单元教材分析
二、察学情——“量”“率”同行,“双线”并进有基础
整合教材的研究一定要关注学生学情,离开了学情,一切整合都没有任何意义。笔者对三所不同层次学校的136 名学生进行前测,前测问题及前测结果如下。
问题1:你知道“分数”这种数吗?如果知道,请告诉老师你是怎么知道的。
将近一半的学生认识或者听说过分数,也会用自己的语言表达(如图3)。因此,对于经验并不丰富的学生,教师只要在课堂上让数学与生活建立沟通,就可以帮助学生理解分数。
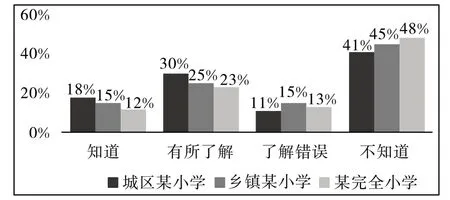
图3 学生回答问题1的情况

图4
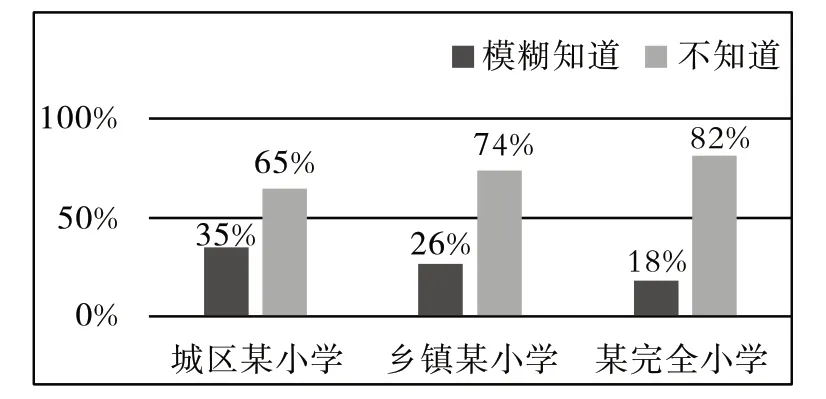
图5 学生回答问题2第(1)题的情况
对于第(2)题,虽然存在画错的情况,但有不少学生能基本画对,画错的学生基本是先将圆分成了2份,再将其中1份涂色(如图6)。只是不管是表达还是涂色,学生都还未意识到要“平均分”,因此教师要引导学生理解分数中的“分”指的是平均分,因为只有平均分才能产生合适的分数。

图6 学生回答问题2第(2)题的情况
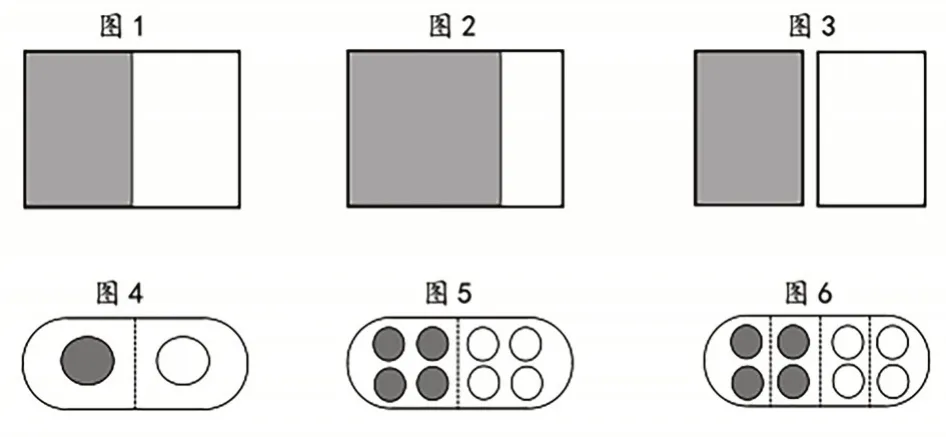
图7

表4 各小学的学生回答问题3的情况
“水有源,故其流不穷;木有根,故其生不穷。”学生有经验,自然就有教育的可能和空间。通过学情分析,笔者认为学生对“量”的分数有更多的知识基础和生活经验,教师只要设计好情境,调动学生已有的经验,引导学生用“熟悉的”去解释“陌生的”,用“形象的”去解释“抽象的”,数学学习就会变得简单有趣。
●践行:整体架构如何定?
对于“分数的初步认识”一课,只关注“量”,或只关注“率”,都会人为地割裂了“分数”的整体性,让学生对后续分数的学习产生“负迁移”。因此,笔者尝试对三年级上册和五年级下册的分数内容进行重组整合。
一、整体架构,重组教材内容
在“分数的初步认识”一课中重组教材内容做“加法”,将“分数与除法”的例1、“几分之一”与“分数的简单应用”的例1 整合为一节课,对接学生的现实起点,体现知识的结构性,在分数概念建构初期帮助学生清晰地认识分数。同时,在教材目标上做“减法”,学生只需感知分数的两重含义,会用简单的语言、涂色、画图等方式来辨别“量”“率”即可。重组整合如图8所示。
打破三年级和五年级的知识边界,将五年级下册“分数与除法”的例1 移至三年级起始课,分解三年级分数的相关内容,将“认识几分之一”和“分数的简单应用”的例1 整合,拓展认识“率”。练习课设计“量”“率”结合的习题巩固新知,后续“认识几分之几”、“分数的简单应用”的例2、“分数的意义”等内容皆“量”“率”并进。对“分数的大小与比较”也做了适当调整,先教学“同分母分数的大小”,后教学“几分之一的大小”。因为认识几分之一和几分之几后,学习“同分母分数的大小”比学习“几分之一的大小”容易。
二、教学实践,寻求“并进”之法
吴正宪老师曾说:“要敢于打乱教材的安排顺序,将教材中容易混淆的概念安排在同一节课中学习,用比较的手段来辨析概念的内涵”“‘量’‘率’本是同根生,教学何不一起行”。 笔者遵循学生学情,起始课是从“量”含义出发带领学生认识分数,利用学生的生活经验引出“率”含义,再“量”“率”并进,呈现分数的全貌。
笔者对“分数的初步认识”一课进行了全新的设计(如图9)。

图9 “分数的初步认识”教学设计
任务一:唤醒经验——创设情境,引出“量”的含义
三年级学生在生活中已经有平均分的经验,有半个、半块、月饼的一半、苹果的一半这样的生活经验。在课堂教学中,若以这些经验为生长点,“生长”出新的知识,就能完成整数到分数的过渡。这样,分数就能在“经验”与“数学”中自然生长,无缝衔接,符合学生的认知发展过程。
【教学片段1】除法的应用
师:什么时候会用除法呢?
生(齐):平均分东西的时候。
师:4个饼平均分给2个人,每人几个?
生1:4÷2=2(个)。
师:其中的4、2、2分别表示什么意思?
(学生回答略)
师:2个饼平均分给2个人,每人几个?
生2:2÷2=1(个)。
师:其中的2、1表示什么意思?
(学生回答略)
师:1个饼平均分给2个人,每人几个?
生3:1÷2……
师:每人得到几个?
生4:半个。
“平均分”这一概念是学生认识分数的重要基石。教学从学生熟悉的平均分引入,先回顾除法中蕴含的平均分过程,再利用“1÷2=”这一问题激活学生认识新知的动力,同时也阐明了分数产生的价值所在,为学生后续的学习做好铺垫。
任务二:转换经验——自主探究,构建“量”的特征
教育并不是一件“告知”和“被告知”的事情,而是一个主动的、建设性的过程。虽然不同的教学方式都能让学生学会知识,但给学生带来的学习感受却千差万别。自主探究能让学生在探寻知识的过程中有不同的收获。
师(出示月饼图,图略):请分一分这个月饼,怎么分?不对折可以吗?
(学生回答略)
师:把这个月饼平均分成2份,其中1份就是你们说的半个,半个还可以表示为个。
(学生回答略)
师(出示三种分月饼的方法,如图10 所示):它们分成的每一份都是个吗?
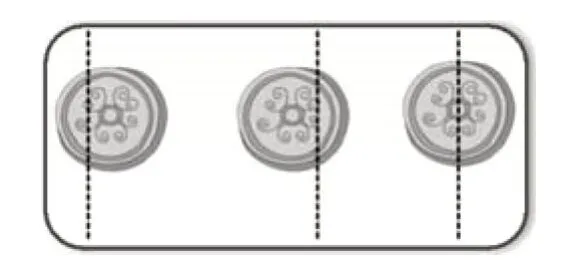
图10
(学生回答略)
师:之前我们分1 个月饼,分得的月饼不是整个的,分数就出现了。
师(出示图11):看图,请按“把()平均分成2份,其中1份就是()”说一说。

图11
师:不管是分什么东西,只要是平均分成2 份,其中的1份就可以用个或颗或根来表示。
师(出示图12):用分数表示涂色部分。
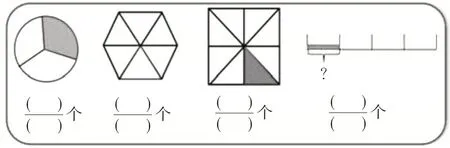
图12
教师提供丰富的素材,通过不同素材的比较和概括,学生可以更深入地理解分数的形成过程。在板书和课件上完整呈现数学语言,并帮助学生表达,是一种很有效的教学策略。因为在一次次的表述和讨论中,学生能够感受到分数与其他概念之间的联系和区别,进一步加深对分数的理解。
师:这张纸除了可以平均分成2 份,还可以平均分成几份呢?
(教师展示学生作品,如图13所示。)
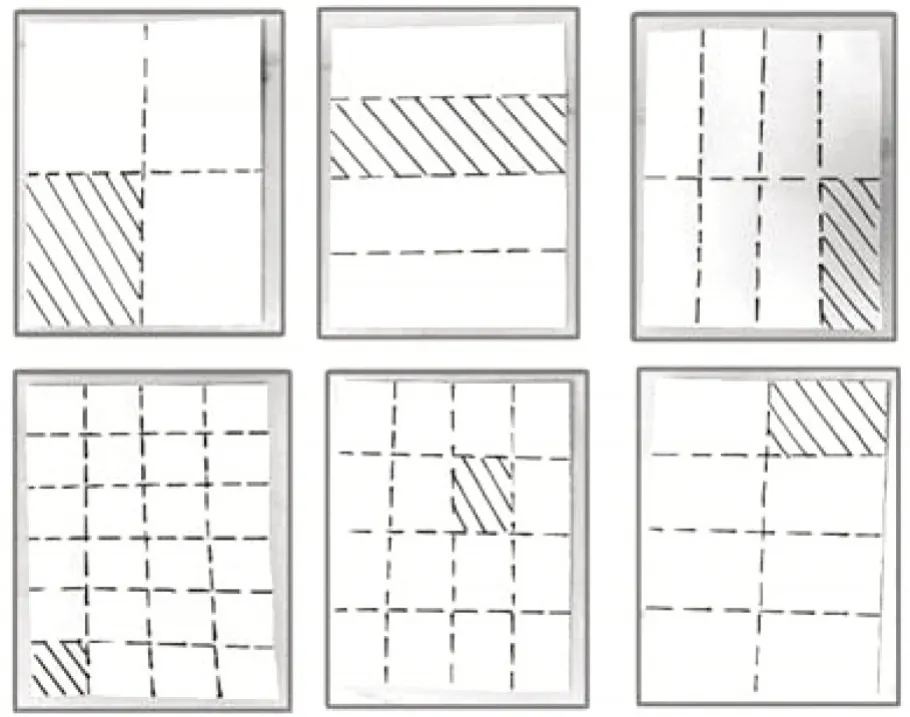
图13
任务三:对接经验——与生活对接,揭示“率”的含义
“种子”的力量在于生长。对“种子课”中新概念的认知越全面,在之后的“生长课”教学中,学生就能够更高效地学习新知,进而实现“减负增效”的目标。
【教学片段5】关联“量”与“率”
生1:平均分得来的。
师:是的,把1 个月饼平均分成2 份,其中1 份就是半个,也就是几个?
师:也有小朋友说这1 份是月饼的一半,一半怎么表示呢?
(教师出示练习,如图14、图15所示。)

图14

图15
从“量”到“率”的过渡,一直是整个教学设计中的难点。生活中,将一个月饼平均分给2 个人,通常会说每人得到“半个”或者是“月饼的一半”。“半个”对应分数中“量”的含义,即“个”;而“一半”则对应“率”的含义,即“月饼的”。教学从学生的生活出发,自然实现“量”“率”的衔接。
任务四:超越经验——由“1”及多,助推“率”的生长
学生是发展中的人,教学中要关注学生的发展,要用发展的眼光看待学生。要想学生“跳起来摘桃子”,那么适当的拓展就必不可少。如从“一个物体”延伸至“一些物体”,学生就能感知每一个“率”都有其对应的“量”,“量”和“率”是相辅相成的。
【教学片段6】拓展延伸
师(出示图16):把2 个月饼平均分给2 个人,每人得到了1 个,那么这1 个是2 个月饼的几分之几?
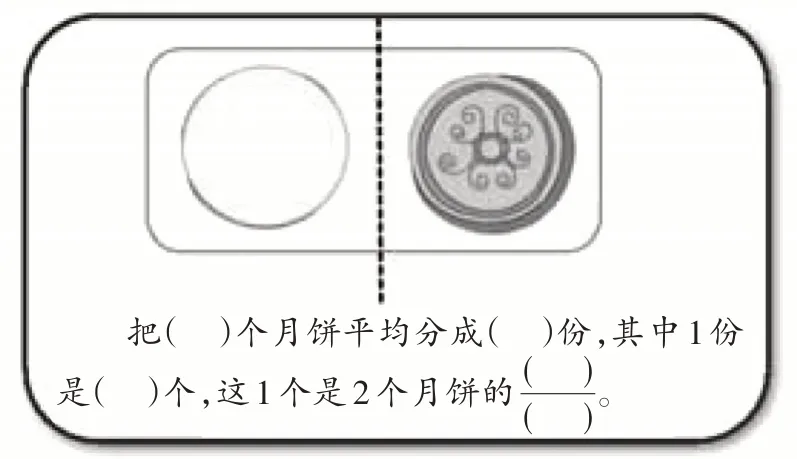
图16
师(出示图17):4 个月饼,平均分给2 个人,每人得到2个,这2个是4个的几分之几?

图17
师:分数不仅可以在分1 个月饼时用,在分2个、4个等多个月饼时也可以用。
师:回答以下几个问题。
此拓展环节中,由平均分1 个月饼回到平均分2 个、4 个月饼,与教学初环节相似却更进一步,让学生从“1”走向“多”,建立起“一个整体”的概念,帮助学生打通理解“量”与“率”的节点。因此,在认识“一个整体”的几分之一时,表示“量”和“率”的分数含义得以真正凸显,学生也就能够清晰感知分数的两层含义。
●反思:“量”“率”并进也能“行”
“量”“率”并进效果如何?笔者对试教的两个班级进行了后测,问题如图18-1 所示,结果如图18-2所示。
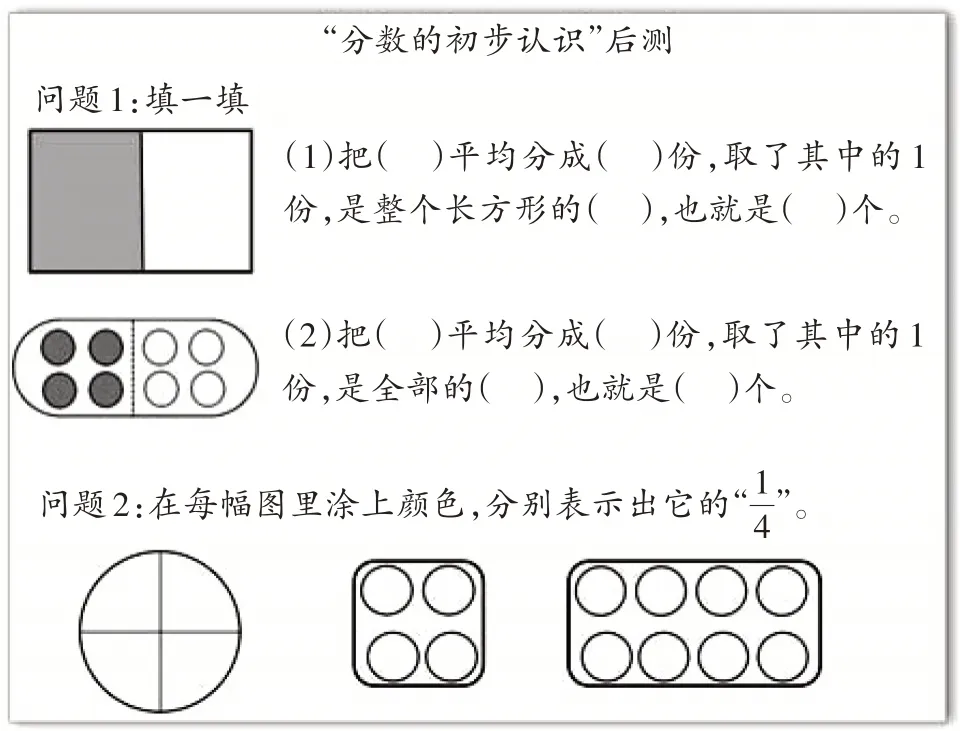
图18-1 后测问题

图18-2 两个班级的后测结果
后测结果显示,三年级学生具备了辨析分数“量”“率”双重含义的能力,“量”“率”并进是可行的。
“量”“率”并进的整体教学思路,不仅能丰富分数认识的维度,同时也解决了学生后续学习“小数的初步认识”中的认知断层问题,学生在今后学习分数时不再“望而却步”,同时增强了学习自主性。综上所述,“量”“率”并进有需求,有基础,也有方法。“量”“率”本一体,无须先后行。
“权威的教材也要敢于动刀。”这是成尚荣先生对新一轮基础教育课程十年改革的概括和判断,这样坚定回答的底气来源于“以生为本”的教学理念。当然,对分数“量”“率”并进的可行性进行实践尝试,不能仅停留在“种子课”的实践中,在后续的教学中也应一以贯之。
