结构生长:思维从“分化”走向“融合”
——“认识周长和面积”教学实践与思考
2024-04-12江苏如皋市外国语学校226500
江苏如皋市外国语学校 (226500) 丁 洪
周长和面积是测量专题教学的两个重要内容。事实上,物体表面的周长和面积同时存在,如数学书封面一周边线的长就是它的周长,数学书封面的大小就是它的面积;封闭平面图形的周长和面积兼而有之,如长方形一周边线的长就是它的周长,长方形内部的大小就是它的面积。应该说,对于同一个测量对象而言,周长和面积显然“和谐共生”,不可分割,但是它们明显“合而不同”。
考虑“怎么教”之前首先要考虑“教什么”。就周长和面积而言,先教周长,后教面积,是现行大部分教材编排的选择。从知识本位角度来看,这样的编排遵循了知识的内在逻辑,它较为理性地从“一维的线”逐步过渡到“二维的面”,专题教学似乎试图通过时间差,努力实现知识点的个别强化和稳步推进,线性处理的痕迹一览无余。但是,从学生本位角度来看,这样的编排有人为割裂之嫌,一方面它忽视了知识的整体建构,使得周长的教学对面积“视而不见”,面积的教学也对周长“避而不谈”,学生获得的只是单个的知识点,而非是对测量对象的结构把握;另一方面它忽视了学生的认知特点,因为小学生空间观念的建立存在特殊性,根据“混而不错”的现实路径,学生完整经历的是体—面—线—面—体的体验过程,进一步说,学生对面积大小的感觉要比对周长长短的感觉更为强烈,如果单纯学习周长而压抑对面积的认知,或者是单纯凸显面积不去关联周长,教师的教会显得不自由,学生的学会显得不自在,空间观念的渗透会显得不自然。
想要走出现实困境需要付诸行动。教学先从学生熟悉的平面图形入手,以“外描线段”引出周长,以“内刷表面”引出面积,然后紧扣周长和面积的本质内涵,通过看、数、悟等不同层次的链式对比,有序“生长”出相关的概念、判断和推理的能力,最终在变与不变的思辨中实现智慧学习。
一、联中比——生长出概念
(一)猜一猜
师(出示积木):仔细观察,你看到了哪些熟悉的立体图形?请说出它的名字和特征。
(学生辨认长方体、正方体、圆柱等立体图形,并用手势和语言描述各图形的特征。)
师(出示图1):如果像他们这样分别描出立体图形的一个面,你猜描出是什么平面图形?

图1
(学生在抢答中快速确认描出的是长方形、正方形、三角形和圆。)
(二)描一描
师:长方形是由几条线段围成的?正方形和三角形呢?描一描、数一数。
生1:长方形是由4条线段围成的。
生2:正方形也是由4条线段围成的。
生3:三角形是由3条线段围成的。
师:像这样,就能描出平面图形的所有边线(操作略)。
(三)刷一刷
师:这里有一把小刷子,咱们一起给长方形内部刷上颜色。
师(在长方形内部横着刷一部分,指着留白的地方):刷好了吗?
生4:没有。
师:为什么?
生5:还有空白,还要刷。
师:再刷一刷子,这样就——
生6:刷好了。
师(出示正方形和三角形):这两个图形的内部可以怎样刷色?
(学生回答略)
(四)理一理
师(出示图2):长方形所有边线的长度,就是它的周长。长方形整个表面的大小,就是它的面积。显然,长方形既有周长,也有面积。那正方形和三角形呢?

图2
生7:正方形既有周长,也有面积。
生8:三角形既有周长,也有面积。
师(出示其他平面图形,图略):这些平面图形也有周长和面积吗?
生9:都有。
师:看来,平面图形既有自己的周长,也有自己的面积。今天,我们就来认识它们。(板书课题:认识周长和面积)
【思考:概念的建立是理性认识的初级阶段。新概念往往表现出基础性、生长性和发展性的特征。首先,“描一描”调用了“长方形和正方形的直观认知”和“线段认知”,如果把“描”出的每一根线段看成是局部理解(有具体长度),那么“描出平面图形的所有边线”就为平面图形周长概念的建构做了铺垫。其次,“刷一刷”调用了“长方形和正方形的直观认知”和“面的大小感知”,“刷好了吗?”的追问是激活学生对图形大小的经验,而后续更换刷色对象则是迁移和强化认知体验,使得要求“刷出平面图形的整个表面”变得像呼吸一样自然。最后,“编筐编篓重在收口”,一方面直观地揭示了周长和面积的数学本质,实现了概念从“感性”到“理性”的必要切换;另一方面通过结构化定性“长方形既有周长也有面积”,驱动学生即时练习、迁移内化和形成表象,使学生经历概念从“特殊”到“一般”的螺旋上升的过程。】
二、看中比——生长出判断
(一)剥一剥
师(拿出一个长方形塑料板,请学生用手指描一描周长,用手掌刷一刷面积):接下来,老师要变个魔术——把长方形塑料板的一周边线全部“剥”下来,请仔细观察。
师:现在终于“剥”完了它的一周边线。把它拉直了,其实就是——
生1:一根长长的线段。
师:它里面包含几根小线段?
生2:4根。
师:这根线段的长度就是这个长方形的——
生3:周长。
(二)辨一辨
师(出示图3):大家表现得真好!给大家奖励一颗五角星。如果要将这颗五角星的周长描下来,这样描对吗?
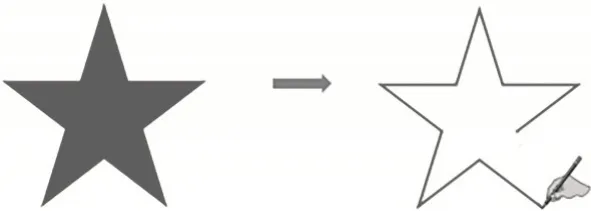
图3
生4:不对,少描了一条线段。
师:要想表示五角星面积,该怎么样去刷色?
生5:把它刷满,就像左边五角星的样子。
师:看来,周长就是一周边线的长度,一条边都不能缺(板书:一周边线的长)。面积就是图形内部的大小,一块面都不能少(板书:图形内部的大小)。
(三)比一比
师(出示图4):这里有两个长方形,用一种颜色的水彩笔描出它的周长,用另一种颜色的水彩笔涂出它的面积,请动手试一试。
图4
(在学生画完后,教师组织学生重点交流“周长在哪里”和“面积在哪里”。)
师:哪个图形的面积比较大?哪个图形的周长比较长?
师:借助所画作品,与同桌说清楚“周长怎么比?面积怎么比?”。
生6:面积比的是图形内部的大小,我能直接看出来,左边长方形的面积比较大。周长比的是一周边线的长,分别比上边、下边、左边和右边,一共比4次,我发现左边长方形的周长比较长。
生7:对于周长,我只要比2 次。先竖着比,发现它们一样长,再横着比,发现左边的长。这样左边长方形的周长就长一些。
师:无论是对应地比4 次,还是根据长方形对边相等的特点巧妙地比2 次,比周长都是在比什么?
生(齐):一周边线的长。
【思考:判断的运用是理性认识的第二阶段。一般概念形成之后,必然跟进相应的判断。具体来说,是否“剥”下了长方形的“一周边线”是第一次判断,其间的追问和互动都指向周长的本质内涵,即图形一周边线的长,不是一根或几根,而是所有边线的总和才能称为周长;五角星的周长“描得对吗?”是第二次判断,通过现场指认、示范修正和描述解释,周长的概念逐渐完整,从而深入人心;第三次判断发生在两个长方形之间的比较,对于“哪个图形的面积比较大?”“哪个图形的周长比较长?”都需要讲清楚“比哪里?”“怎么比?”,无论是一一对应比4次,还是简化之后比2次,其实都是基于概念的判断行为,看似形式不同,其实本质相通。】
三、数中比——生长出推理
师:有一面白色的墙面,需要贴上正方形的瓷砖,先贴上第1块,这一块瓷砖有周长和面积吗?
生(齐):有。
(师生互动,边贴边数第一排瓷砖。)
师(整体出示第二排到第四排瓷砖,并介绍两块花瓷砖,在出示第五排瓷砖之前追问):墙面贴满了吗?
师(出示图5):这两块花瓷砖,你还能一下子看出哪个周长比较长,哪个面积比较大吗?

图5
生1(用手比画):左边的花瓷砖横着长,竖着短;右边的花瓷砖横着短,竖着长,看不出来。
师:怎么办?
师:把小正方形的边长看成1 个长度单位,数一数并标出周长有几个小正方形边长;把小正方形的面积看成1 个面积单位,数一数并标出面积有几个小正方形面积。组内交流“怎么数”和“怎么比”。
生2:左边花瓷砖的周长有12 条小正方形边长这么长,右边花瓷砖的周长也有12 条小正方形边长这么长,它们的周长相等。
生3:左边花瓷砖的面积有8 个小正方形这么大,右边花瓷砖的面积有9 个小正方形这么大。右边花瓷砖的面积大。
师(出示图6):我们是先确定数的单位,再数出单位的个数,然后顺利比出结果。

图6
【思考:推理的介入是理性认识的第三阶段。具体来说,第一阶段是看着不好比,其实质是部分判断之间虽然有联系,但是对于整体“一周边线”而言,并不能将这些单个的判断有机整合而形成新的判断,换句话说,“推理”在这里难以进行;第二阶段是数着比,其实质是借助小正方形瓷砖的边长为1个长度单位,分别数出“周长有12 条小正方形边长这么长”,借助小正方形的面积为1 个面积单位,分别数出“面积有8 个小正方形这么大”和“面积有9个小正方形这么大”。这样,无论是周长,还是面积,因为有了联结的工具,即“相同单位”,所以可以产生新的判断,最终顺利推理出“它们的周长相等”和“右边花瓷砖的面积大一些”的结论。最后,借助动态演示和过程梳理,使得推理的要点和路径得以可视化、结构化和一般化。】
四、悟中比——生长出智慧
(一)初次变
师(出示图7):大正方形瓷砖由9 块小正方形组成。接下来,我要变魔术了,你说变,它就变!

图7
生(齐):变!变!变!
师(出示图8):与原来大正方形瓷砖相比,你能一下子判断下面瓷砖的面积和周长哪个变了吗?

图8
生1:面积肯定变了,因为都少了一些小正方形。
师:有道理。那么,周长到底变了没有?请沿着现在的瓷砖一周边线数一数和比一比。
生2:左边瓷砖的周长有12 条小正方形边长这么长。与原来相比,周长不变。
生3:中间瓷砖的周长有12 条小正方形边长这么长。与原来相比,周长也不变。
生4:右边瓷砖的周长有14 条小正方形边长这么长。与原来相比,周长变了。
师:看来,瓷砖面积都发生变化,但是瓷砖一周边线的长度,有的不变,有的变了。
(二)再次变
师:老师又要变魔术了,先将大正方形瓷砖平均分成两块小长方形,然后拼接;或者,将大正方形瓷砖平均分成两块小三角形,然后拼接。你说变,它就变!
生(齐):变!变!变!
师(出示图9-1、图9-2):与原来大正方形瓷砖相比,你能判断现在瓷砖的面积和周长哪个没有变吗?

图9-1

图9-2
生5:面积没有变,因为没有多一块,也没有少一块。
师:描一描现在瓷砖的一周边线,与大正方形瓷砖相比,哪一部分一样长,哪一部分变化了?
(学生先独立思考,再组内交流,最后汇报。)
生6:我来说图9-1 的瓷砖。它横着的4 条边线与正方形的4 条边线一样长,竖着的2 条边线是多出来的,所以周长变了。
生7:我来说图9-2 的瓷砖。它横着的2 条边线与正方形横着的2 条边线一样长,斜着的两条边线比正方形竖着的边线要长,所以周长变了。
师:先确定一样长的部分,再确定变化的部分,最后合起来推理得到结论。为你们点赞!
(三)终极变
师(出示图10):老师将大正方形瓷砖分割后变成——

图10
生(齐):七巧板。
师:七巧板可以拼接成有趣的图案,你看到了什么?
生(齐):小鱼、小鹅和小羊。
师:你猜,拼成的图案和原来正方形相比,面积变了吗?周长呢?这个问题留给同学们课后思考。
【思考:智慧的演绎是理性认识的综合阶段。只有在认知的最近发展区和稍复杂的境遇下,智慧才能找到迸发的土壤和契机。具体来说,图形第一次的变化较为“温和”,解决面积的变化问题时,有的学生根据“图形内部的大小在减少”,运用概念直接判断,有的学生借助“单位思想”逐步量化,间接地解决问题;解决周长的变化问题时,学生选择了“单位思想”,量化后再比较。这对于三年级的学生来说是可行的,毕竟智慧生长离不开方法的基础迁移。图形第二次的变化较为“剧烈”,原因不在面积(因为可以借助直观演示,运用概念直接判断),关键是周长的变化问题,在问题“与大正方形瓷砖相比,哪一部分一样长,哪一部分变化了?”的引导下,学生将“一周边线”解构成两个部分,先各个击破,然后再有机重构和推理。因为阶段结构认知和理解水平的局限,有时学生智慧的生长仍然需要教师的适时点拨。图形第三次的变化较为“深远”,与前面变化不同的是,七巧板的分割内容和拼接情况更为复杂,这里不需要学生即时回答,而是留下“未完待续”的活动,巧妙地将学习从课堂引向课外,鼓励学生动手操作、对比思考和感悟规律。显然,这样处理,智慧生长的空间已经从“有限精彩”走向了“无限可能”。】
