结构表征:思维从“内隐”走向“外显”
——“连除的实际问题”教学实践与思考
2024-04-12江苏如皋市外国语学校226500
江苏如皋市外国语学校 (226500) 丁 洪
“连除的实际问题”属于数与代数领域内容,主要聚焦“数量关系”和“数的运算”。苏教版教材将它编排在四年级上册第二单元,是在学生已经学习“连乘的实际问题”和“两、三位数除以两位数(不含调商)”等知识基础上教学的。从知识技能看,主要引导学生从不同角度理解、表征和解决连除的相关实际问题,提升“一题多解”的能力,丰富“殊途同归”的认知。从过程方法看,主要引导学生从条件想起,逐步推导出所需结论,唤醒“关系组合”的意识,渗透“由因导果”的策略。从情感态度看,主要激发学生直面问题的探究动能、创造潜能和结构智能,让学生树立“勇于突破”的信心,涵养“理性思维”的品质。
为了提高课堂教学实效,需要关注和思考以下问题。一是为什么这时候学?对此要处理好学生的阶段需求与连除知识的价值,突出关系理解和变式重组,避免“就事论事”和“浅尝辄止”;二是怎么去学?对此要处理好学生除法经验的新旧对接与多元表征,辩证自主探究和共性概括,避免“居于一隅”和“短视行为”;三是学到什么程度?对此要处理好学生除法意义的理解程度与可视表征,建构思维场域和全局视野,避免“碎片思考”和“单向体验”。最终,助力学生建构连除实际问题中“类型不同,结构相通”的横向认知,以及连乘连除实际问题中“方向不同,结构相联”的纵向认知,提升连除运算能力,发展结构化思维素养。
一、自主探究,呈现结构
(一)选条件,提问题
师(出示主题图情境,如图1):通过交流,我们已经知道有三个条件(①一共放了224 本书;②2 个书架;③每个书架有4 层。)和一个问题(平均每个书架每层放多少本书?)。现在,请你选两个条件,说说解决问题时可以先算什么。
生1:根据条件①和条件②,可以先算平均每个书架的本数。
生2:根据条件②和条件③,可以先算两个书架一共的层数。
生3:根据条件①和条件③,可以先算两个书架同一层的本数。
师:看来,根据两个有联系的条件可以提出并解决一个一步计算的问题。
(二)画过程,明算理
师:顺着这些思路,怎么解决每个书架每层的本数的问题?(出示活动要求:将长方形看成总本数,选择其中一种方法,在图形中画出过程;比一比,看谁想得明白、画得清楚、算得正确;先独立思考,再在组内交流。)
生4(出示图2):先将长方形平均分成2 份,列式224÷2=112(本),算出每个书架的本数;再把一个书架上的本数平均分成4 份,列式112÷4=28(本),算出平均每个书架每层的本数。因此,就涂这样的一份。

图2
生5(出示图3):先算两个书架一共的层数,2×4=8(层),对应地将长方形平均分成8 份,涂出其中的一份;再用224÷8=28(本),算出平均每个书架每层的本数。

图3
生6(出示图4):先将长方形平均分成4 份,列式224÷4=56(本),算出2个书架同一层的本数;然后选择第一层再平均分成2 份,涂出其中的一份,列式56÷2=28(本),算出平均每个书架每层的本数。
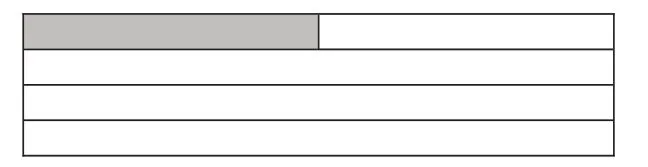
图4
师:能依次列出相应的综合算式吗?
生7:224÷2÷4=28(本)。
生8:224÷(2×4)=28(本)。
生9:224÷4÷2=28(本)。
(三)比异同,理结构
师:比较画图和列式的过程,你有什么有趣的发现?
生10:虽然运算的顺序不同,但是条件相同,所以结果一样。
生11:我发现图2 和图4 是一步一步地平均分的,而图3是先求“总层数”,然后一起平均分的。
生12:每种方法中画图顺序和列式顺序是对应的,都画了两次,也算了两次。
师:大家想象一下,图2、图3、图4 和图1 中书架的结构能完全重合吗?
生13:能。如果把图2 从左往右补全,图4 从上往下补全,那么三幅图形的结构与书架结构就是一样的。
生14:其实,书架个数对应图形竖排个数,书架层数对应图形横排个数,书架结构与图形结构刚好一一对应。
师:真好!通过实际问题的解决和比较,我们基本弄清了连除算理和思维关键,也初步体验到连除特点和结构联系,这就是我们今天研究的内容。
(板书课题:连除的实际问题)
【思考:“连除问题”是由两种简单的、关联的“一步除法”组合而成。其中,“等分除”可以细分为“连续等分”和“整体等分”两种情况,思维结构体现“一维线性”向“二维平面”的转变。由于例题中的数据较小,计算难度仅限于“两、三位数除以一位数”,所以教学重心不在于“算法技能”的娴熟精进,而在于“算理本质”的深度理解。首先,通过条件的自由选择和组合描述,引导学生感受“先算什么”的起点不同、条件关联和结果唯一,为连除问题“一题三解”奠定方法基础,指明操作路径。其次,借助“分步计算”和“画图示意”的同构活动,引导学生通过不同方式合理表征连除算理,强化“怎样算”与“怎样画”的程序对应、思维互动,并在此基础上,借助综合算式记录连除过程,进一步凸显问题的结构特征。最后,通过对比反思三种方法,驱动学生有序梳理条件和问题、着力分析思维过程,初步实现连除的外在算法与内在算理的认识融合,尤其是图形与书架的结构联结,更为后续结构化学习做好必要铺垫。】
二、灵活检验,对比结构
师:想一想,这题的结果可以怎样检验?
(学生先独立思考,再组内交流。教师巡视,提醒学生用联系的眼光看问题。)
生1:可以用不同的方法再做一次。
生2:因为用三种方法解题,虽然先算的内容不同,但是最后的结果必须一样。
师:还有其他检验方法吗?
生3:我们组认为,可以把“商28本”代入原题,倒过来用乘法算一遍,看一看“2 个书架是不是一共有224本书”。
师:请具体说说怎么想和怎么算的。
生4:先算一个书架的本数,再算总本数,列式28×4×2=224(本)。
生5:先算两个书架的总层数,再算总本数,列式2×4×28=224(本)。
生6:先算两个书架同一层的本数,再算总本数,列式28×2×4=224(本)。
师:回顾检验的过程和方法,你有什么发现?
生7:我发现“一共有224 本书”从条件变成问题,而“每个书架每层28本”从问题变成条件。
生8:我发现“总本数”“架数”“层数”和“每个书架每层的本数”这些信息之间有联系,知道其中的三个信息,就可以求出剩下的信息。
生9:连除和连乘的运算顺序变化了,同一种方法的图形结构没有变化,但是观察的方向相反。
师:看来,“被除数÷除数÷除数=商”,既可以交换除数位置,顺向思考,用除法检验除法,也可以用“商×除数×除数=被除数”,逆向操作,即用乘法检验除法。
【思考:验算是连除学习中的重要环节。验算不是机械地摘抄数据凑答案,而是经验的有效连接和习惯的品质培育和认。具体来说,一方面是“顺向经验”的激活,通过“怎么想到”的方法溯源,对比“数位置”与“式结构”,进一步体验连除运算“不同方法”的外形结构、思维特点和内涵实质。另一方面是“逆向经验”的激活,通过说清楚“先算什么”和“再算什么”,列综合算式感知“连乘结构”,并在对比、联系和发现中,进一步感悟“连除算”与“连乘算”之间的思维互逆、结构统一和认知平衡。】
三、多向实践,迁移结构
(一)求单量,悟等分
1.排队问题
出示情境(如图5):四年级168 学生去参观科技馆,平均分成4队,每队平均分成3组。每组有多少人?

图5
师(出示图6):先用结构图梳理条件和问题,再说说怎么想和怎么算。
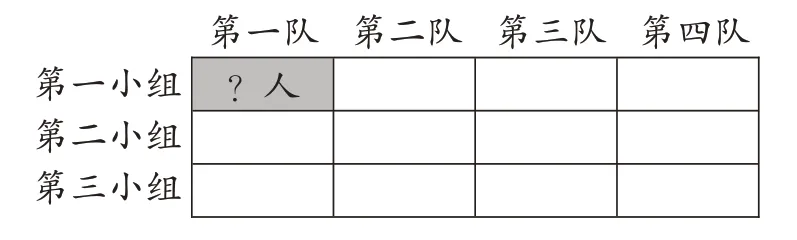
图6
师:请具体说说怎么想和怎么算的。
生1:我先竖着看,用168÷4=42(人),算出每个队的人数,再横着看,用42÷3=14(人),算出每组人数。综合算式为168÷4÷3=14(人)。
生2:我是整体看的。先用4×3=12(组),算出小组的总数,再用168÷12=14(人),算出每组人数。综合算式为168÷(4×3)=14(人)。
生3:也可以先横着看,用168÷3=56(人),算出4 个队同一组的人数;再竖着看,用56÷4=14(人),算出每组人数。综合算式为168÷3÷4=14(人)。
师:其实,先等分“队数”再等分“组数”,或者先等分“组数”再等分“队数”,都是连续等分除。而先算“总组数”再算“每组人数”,则是整体等分除,殊途同归。
2.吃虫问题
出示情境(如图7):三只燕子一个星期吃924只害虫。平均每只燕子每天吃多少只害虫?

图7
师(出示图8):先用结构图梳理条件和问题,再说说怎么想和怎么算。
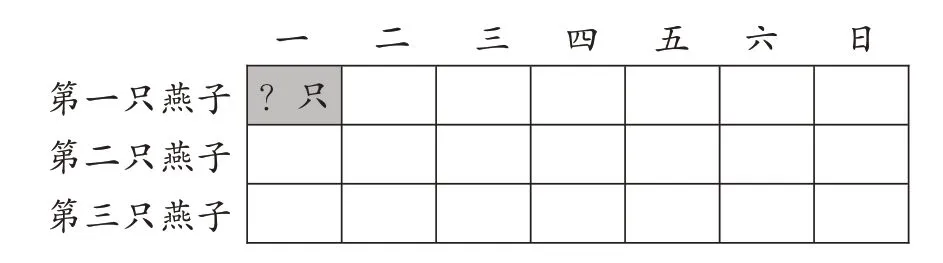
图8
生4:我先竖着看,用924÷7=132(只),算出3只燕子1天吃害虫的总只数,再横着看,用132÷3=44(只),算出平均每只燕子每天吃害虫的只数。综合算式为924÷7÷3=44(只)。
生5:我先横着看,用924÷3=308(只),算出1只燕子7天吃害虫的总只数,再竖着看,用308÷7=44(只),算出平均每只燕子每天吃害虫的只数。综合算式为924÷3÷7=44(只)。
生6:也可以整体看,先用7×3=21(只),算出7天里燕子出现的总只数,再用924÷21=44(只),算出平均每只燕子每天吃害虫的只数。综合算式为924÷(7×3)=44(只)。
师:其实,先等分“天数”再等分“只数”,或者先等分“只数”再等分“天数”,都是连续等分除。而先求“7 天里燕子出现的总只数”再算“平均每只燕子每天吃害虫的只数”,则是整体等分除。它们的道理是相通的。
(二)求数量,悟包含
1.吃药问题
出示情境(如图9):一瓶药共150片,王大伯每日吃3次,每次2片。这瓶药可以吃多少天?
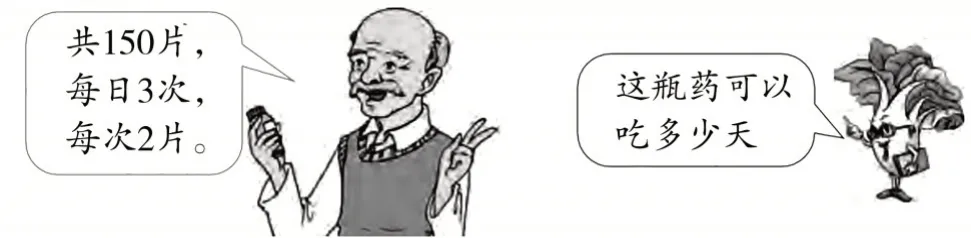
图9
师(出示图10):先用结构图梳理条件和问题,再说说怎么想和怎么算。

图10
生7:我先竖着看,用2×3=6(片),算出一天吃的片数,再横着看,用150÷6=25(天),算出这瓶药片包含几个6 片,也就是吃的天数。综合算式为150÷(2×3)=25(天)。
生8:我是从整体看的。先用150÷2=75(次),算出吃的总次数,再用75÷3=25(天),算出以3 次为一天吃的天数。综合算式为150÷2÷3=25(天)。
生9:也可以先横着看,用150÷3=50(片),算出所有早上吃的片数,再竖着看,用50÷2=25(天),算出吃了几个早晨,对应的就是几天。综合算式为150÷3÷2=25(天)。
师:其实,先算“一天吃的片数”再算“天数”,是整体包含除;而先算“总次数”或“同一时段吃的总片数”,再算“天数”,则是连续包含除,目标一致。
2.包装问题
出示情境(如图11):有一种面包的包装是2个装一袋,4袋装一盒。104个面包一共可以装多少盒?
图11
师(出示图12):先用结构图梳理条件和问题,再说说怎么想和怎么算。

图12
生10:我先竖着看,用2×4=8(个),算出一盒面包的个数,再横着看,用104÷8=13(盒),算出一共装的盒数。综合算式为104÷(2×4)=13(盒)。
生11:我是从整体看的。先用104÷2=52(袋),算出包装的总袋数,再用52÷4=13(盒),算出一共装的盒数。综合算式为104÷2÷4=13(盒)。
生12:也可以先横着看,用104÷4=26(个),算出每盒中第一袋位置上的总个数,再用26÷2=13(盒),算出包含几个第一袋,对应的就是几盒。综合算式为104÷4÷2=13(盒)。
师:其实,先算“一盒个数”再算“盒数”,是整体包含除;而先算“总袋数”或“同一位置上的总个数”,再算“盒数”,则是连续包含除。这两种算法同样精彩。
【思考:“等分除”和“包含除”的运算基础都是“平均分”,思维结构必然关联,但学生对除法意义的体验有所区别。具体来说,一是借助“排队问题”和“吃虫问题”,顺势迁移解决“书架问题”时的表征结构、观察角度和思考流程,明确“连续等分”和“整体等分”的外在算式差异,凸显“一题三解”的内在结构统一,侧重“等分除”的原始模型,即“总量÷数量=单量”的认知生长和有序建构。二是借助“吃药问题”和“包装问题”,顺势呈现“连续包含”和“整体包含”的连除结构,促使学生感受到连除类型虽然发生变化,但是其算理和算法依然统一,凸显“包含除”的原始模型,即“总量÷单量=数量”的认知生长和有序建构。显然,这样的结构表征能够助推学生思维外显,增强学生结构思维的意识激发,帮助学生的整体理解和认同策略。】
四、反思概括,内化结构
师(出示所有的图形结构,如图13):千金难买回头看。观察和对比这些图形结构,你有什么体会?
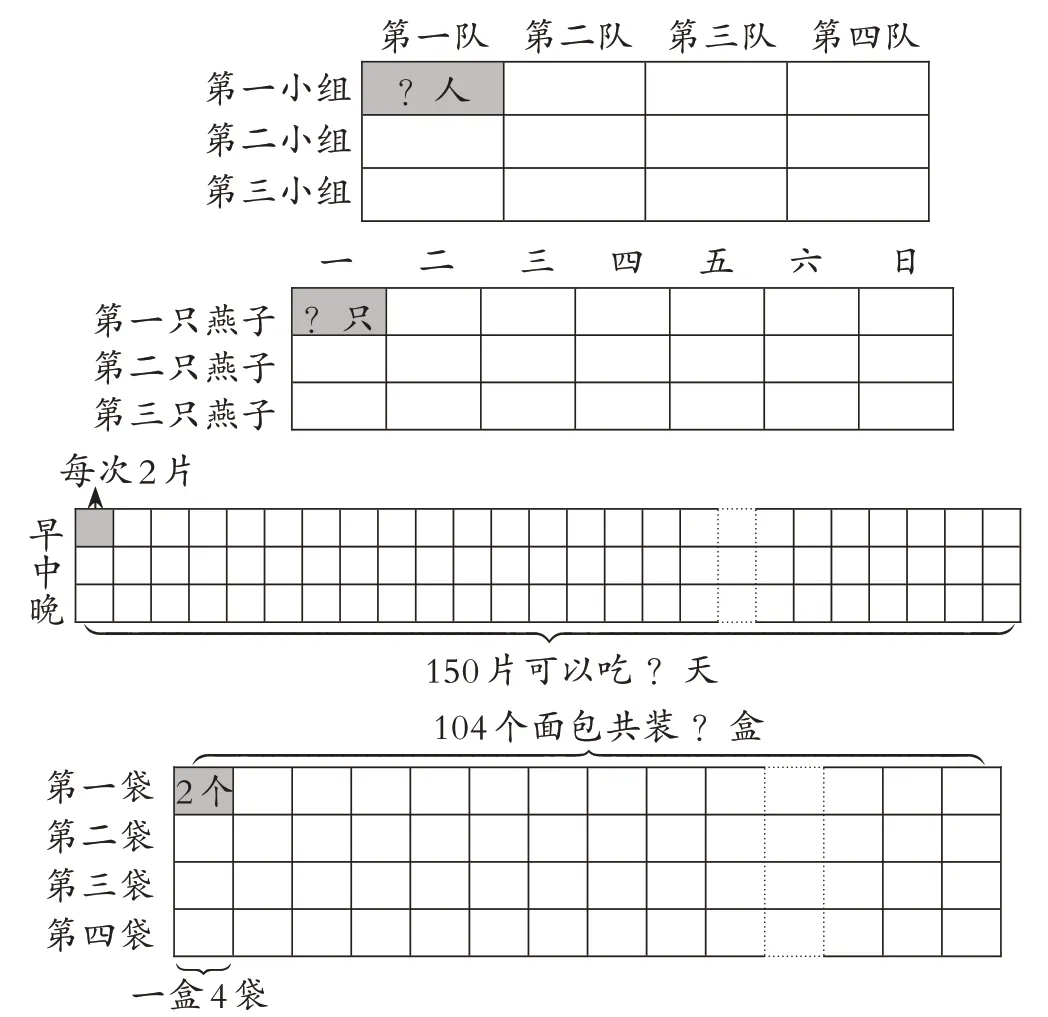
图13
生1:我觉得这类问题从条件想起比较方便。
生2:我发现连乘是求“总量”,需要把“单量”合起来,连除是求“单量”或者“数量”,需要把“总量”平均分。
生3:我来补充。连除中求“单量”是等分除,可以“连续等分”或“整体等分”;连除中求“数量”是包含除,可以“连续包含”或“整体包含”。
师:爱动脑,会思考,为你们点赞!在解决连除的实际问题中,角度“怎么看”与条件“怎么选”同步,图形“怎么画”与算式“怎么列”同构,有了结构图的呈现、连接和助力,我们的思维才能变得有抓手、有方向和看得见。
【思考:反思是基于知识又超越知识的能动行为。具体来说,一是对连除的实际问题解决过程的反思,主要建构策略介入、算式表征和检验方法的一般性,“就事论事”的意味较浓;二是对连除的实际问题的认知提炼,主要建构图形结构、程序推演和思维双向的一致性,“深入浅出”的诉求明显。显然,两种反思都有价值、融合共生,助推学生数学精神、思想和方法的有序生发与有效沉淀。】
