钢中不同形状夹杂物在超重力场中上浮模拟研究

2024-04-12段禹奇郭占成

工程科学学报 2024年5期

段禹奇，郭磊，张帅，郭占成

北京科技大学钢铁冶金新技术国家重点实验室，北京 100083

提升钢的洁净度一直是钢铁冶金领域研究的重点，而非金属夹杂物则是洁净度的重要影响因素. 相关研究表明[1-2]，致使轴承钢发生滚动接触疲劳失效的内因是夹杂物引起的疲劳裂纹. 不同形状、类型的夹杂物其对钢的破坏机理与有害程度存在明显区别[3]. 目前传统的钢液精炼除杂方法，多数因产生搅动而导致返混，而单纯利用密度差使夹杂物自然上浮去除虽可以避免返混，但其需要的上浮时间过长，且对小尺寸夹杂物的去除效果不佳[4].

不同的夹杂物的来源、形状、密度、构成、尺寸以及变形性都有所不同，其对钢材性能的影响也各不相同，因此需要从多种角度对夹杂物进行分类、解释以及总结[3,5-13].

超重力是一种非接触的体积力，当两相间存在密度差时，超重力能够强化两相分离. 将超重力技术应用于去除金属熔体中的杂质目前已有基础研究成果[14]，718合金中的氮的质量分数去除至0.001425%[15]、GCr15轴承钢中氧的质量分数最低可去除至0.00017%[16]，充分说明了超重力去除钢液中夹杂物的可行性.

许多学者通过数值模拟研究夹杂物在金属溶体中的上浮行为. Liu等[17-18]使用流固耦合模型建立了常重力条件下钢中非金属夹杂物上浮去除模型，讨论了夹杂物尺寸对其上浮速度及去除行为的影响. 宋高阳[19]利用DPM离散相模型首次建立了超重力场下夹杂物上浮富集模型. 杜伊诺[20]将超重力应用于流固耦合模型中，揭示了钢液中不同尺寸夹杂物在不同超重力系数下的上浮行为.

钢中夹杂物构成成分不同，其形状也不同. 郭洛方[21]依据分形理论建立了不规则形貌夹杂物的分形维数和动力直径与其上浮速度之间的定量关系. 王敏[22]通过水模拟实验对不同形态夹杂物上浮速度进行排序，并获得了对应的修正系数，同时发现复杂粒子在上浮过程中的运动方式差异会对其上浮速度产生影响.

在前人所做的数值模拟研究中，DPM离散相模型不考虑颗粒体积，无法通过模拟确定到夹杂物上浮行为是否会因为颗粒形状而产生变化；流固耦合模型则会考虑颗粒的体积及形状. 流固耦合模型可以跟踪计算固体边界，根据这一模型特性，可自由构建夹杂物形状进行数值模拟研究；但前人使用流固耦合对夹杂物的上浮研究中均简单地将夹杂物视为球形，并未考虑夹杂物形状对其上浮行为产生的影响，未能完全利用该模型特性.因此，本文首次将夹杂物形状、超重力技术、流固耦合模型相结合，分析讨论不同类型夹杂物在超重力场中的上浮行为.

1 建模方案

1.1 控制方程

对于流体流动过程，对应的控制方程为Navier–Stokes方程和连续性方程，前者描述动量守恒，后者表示质量守恒.

式中：ρ为流体密度，为流速，为单位矩阵，μ为流体黏度，p为压强，t为时间，g为重力加速度，F为作用在流体上的外力.

当夹杂物尺寸较小时，方程中的黏性力远大于惯性力，此时流体流动被称为蠕动流（斯托克斯流），方程（1）可简化为：

流固耦合（Fluid–solid interaction，FSI）用来计算流体与固体之间的相互作用力，流固耦合基于一种任意拉格朗日–欧拉（Arbitrary Lagrangian–Eulerian，ALE）方法，使用ALE公式计算流体与固体间相互作用力，并根据固体边界的移动控制流体域的几何变化：

1.2 几何模型与网格划分

为了研究夹杂物形状对其上浮行为的影响，在二维纵切面中构建了如下三种形状的夹杂物，并分别将三种形状夹杂物命名为A、B、C，如图所示. 非球形的夹杂物拥有较高的形态比（长度/宽度）[23]，本文选取夹杂物的长度dl作为夹杂物的颗粒尺寸. 本研究中所涉及到的夹杂物尺寸dl为1、2.5、5、10及20 μm（夹杂物在求解器内计算时尺寸略有误差，误差约为dl的3%～5%，在可接受范围内）. 夹杂物应能够充分上浮并拥有足够的空间在水平方向上自由移动，设置模拟的相场范围为125dl高、100dl宽的矩形区域，如图1所示.

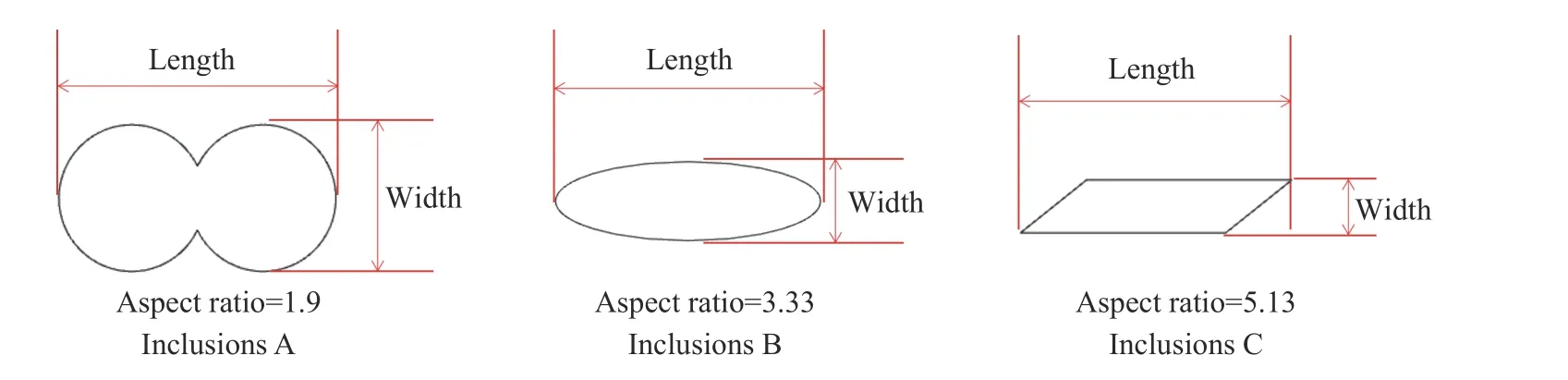
图1 模拟使用的三种夹杂物形状及编号示意图Fig.1 Schematic of the three inclusion shapes and numbers used in the simulation

为了提升求解收敛性的同时节省计算量，使用COMSOL Multiphysics多物理场仿真软件依据物理场自动划分三角形网格. 模型应用了动网格，夹杂物移动时其周围网格会被拉伸，导致计算收敛性下降，因此设置求解器跟踪检测网格的失真度，当检测到失真度高于给定值时，求解器自动重新划分网格以保证夹杂物周围网格始终细密，如图2所示. 整个相场重力方向竖直向下，失真度根据不同尺寸及夹杂物形状在0.1至0.5之间调整以保证求解器能够正常计算；在正式计算前已进行网格失真度（0.1至0.5范围内）对数据无关性验证.

图2 模型计算域与网格划分示意图Fig.2 Schematic of the model computational domain and mesh division

1.3 物理原理及参数

在自然环境中，物体受到的重力为常重力，定义常重力G=1，重力方向始终竖直指向地面. 获得超重力则可以使用旋转离心法[4]，转子绕轴高速旋转产生离心力，该离心力可看做超重力. 在实际工程应用中采用连续式处理方法，设备原理示意图如图3所示，该设备通过转筒旋转提供离心力，钢液由设备上方入口进入，下方入口排出，夹杂物则沿超重力相反的方向移动并聚集在钢液表面. 重力系数G的公式为：

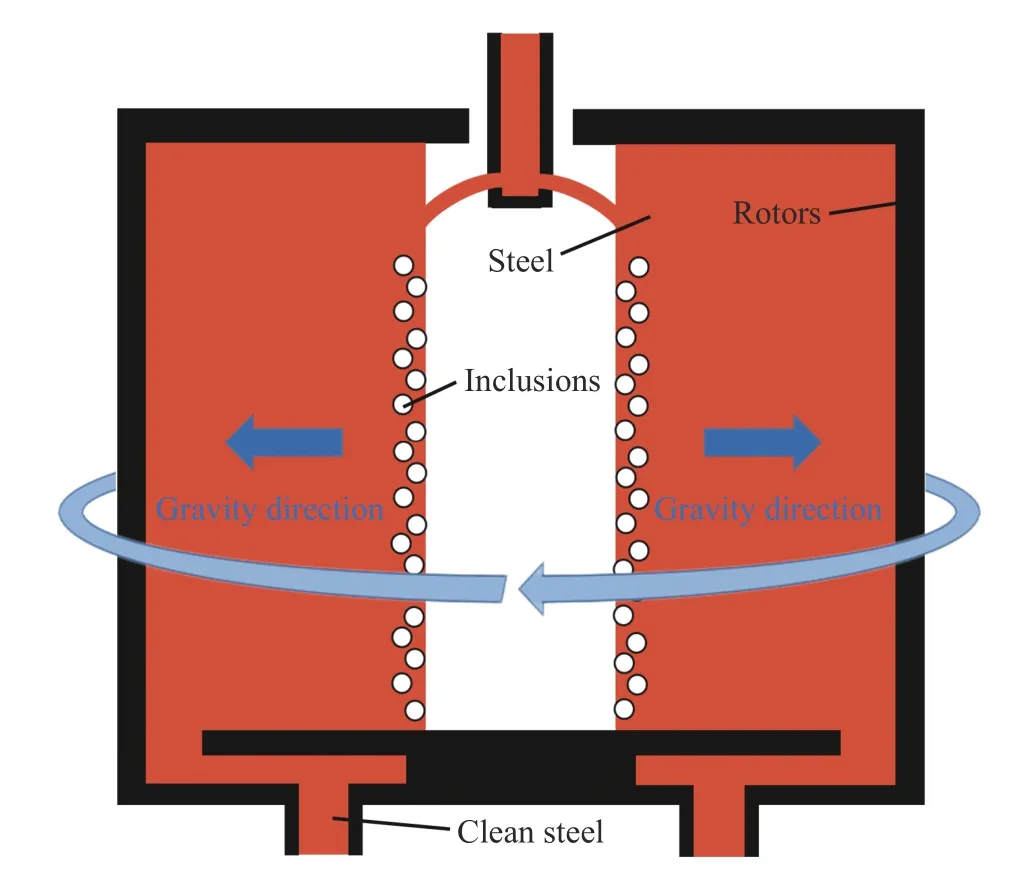
图3 离心装置示意图Fig.3 Schematic of the supergravity device

式中：w为转速，r为离心半径，g为重力加速度.

夹杂物在钢液中的上浮行为本质上即是浮力克服重力及钢液对夹杂物的阻力在与重力相反的方向上做功. 而浮力的产生则是由于夹杂物与钢液存在密度差. 超重力场同时作用于钢液和夹杂物之上，放大了浮力与重力之差，使夹杂物有更大的合力上浮. 模拟所需的物性参数如表1所示.

表1 模型中使用的材料与其参数Table 1 Materials used in the model and their parameters

1.4 边界条件及求解方案

相场的上边界设置为压力为0的开放边界，相场底部和两侧设置为无滑移壁面. 设置夹杂物颗粒为刚体，可自由移动，钢液相区域为动网格的变形域，夹杂物与钢液需分别施加重力系数. 夹杂物初速为0，且以三种不同的角度（0°、45°、90°）放置在钢液中，用以研究初始角度对夹杂物旋转行为影响. 在研究几何形状对夹杂物上浮速度的影响时，将夹杂物以0°水平放置并限制夹杂物的旋转与水平方向的位移，这是为了避免夹杂物细微旋转及水平方向移动对上浮速度产生的影响（夹杂物形状影响旋转及水平方向移动的程度，前期测试约束条件对上浮速度的影响约1%～3%）. 其余研究则会解除限制使夹杂物能够自由旋转与移动.当夹杂物颗粒较小（dl≤10 μm），或重力系数较低时（G≤200）使用蠕动流流体模型进行计算以节省算力，其余则使用层流流体模型运算.

夹杂物自t=0时刻开始上浮，上浮至80dl时停止计算，计算的时间步长为0.0001 s. 模拟采用COMSOL Multiphysics求解器进行求解计算，流固耦合模型设置为双向耦合，运算时流体会对固体（颗粒）边界施加作用力致使颗粒发生移动，而固体颗粒的移动会反作用于流体，继而影响流体状态. 求解器通过迭代计算流场速度、位移场与空间网格位移，计算时根据不同尺寸下模型收敛性的不同调整求解器的最大迭代次数，保证计算正常运行.

2 模拟结果与分析

2.1 不同几何形状对夹杂物上浮速度的影响

在本小节研究中，夹杂物以水平初始姿态开始上浮. 假设夹杂物在上浮过程中只发生垂直方向上的位移，且夹杂物本身不会有自转行为. 在G=1000的重力场下，分别对颗粒尺寸dl=1、2.5、5、10 μm的A、B、C三个形状的夹杂物进行模拟，在上浮80dl距离时采集夹杂物周围流场矢量图像，详见图4. 夹杂物上浮时，带动周围“8”字型区域内的钢液以相同方向运动，夹杂物两侧流场出现低速区（图中深蓝色区域），被夹杂物排开的钢液在低速区回流. 相同尺寸下，虽夹杂物的形状不同，但其周围钢液速度场分布基本相同. 随着夹杂物尺寸的增加，夹杂物的上浮速度加快，其两侧的低速区逐渐后移，尺寸对夹杂物周围流场的影响更大.

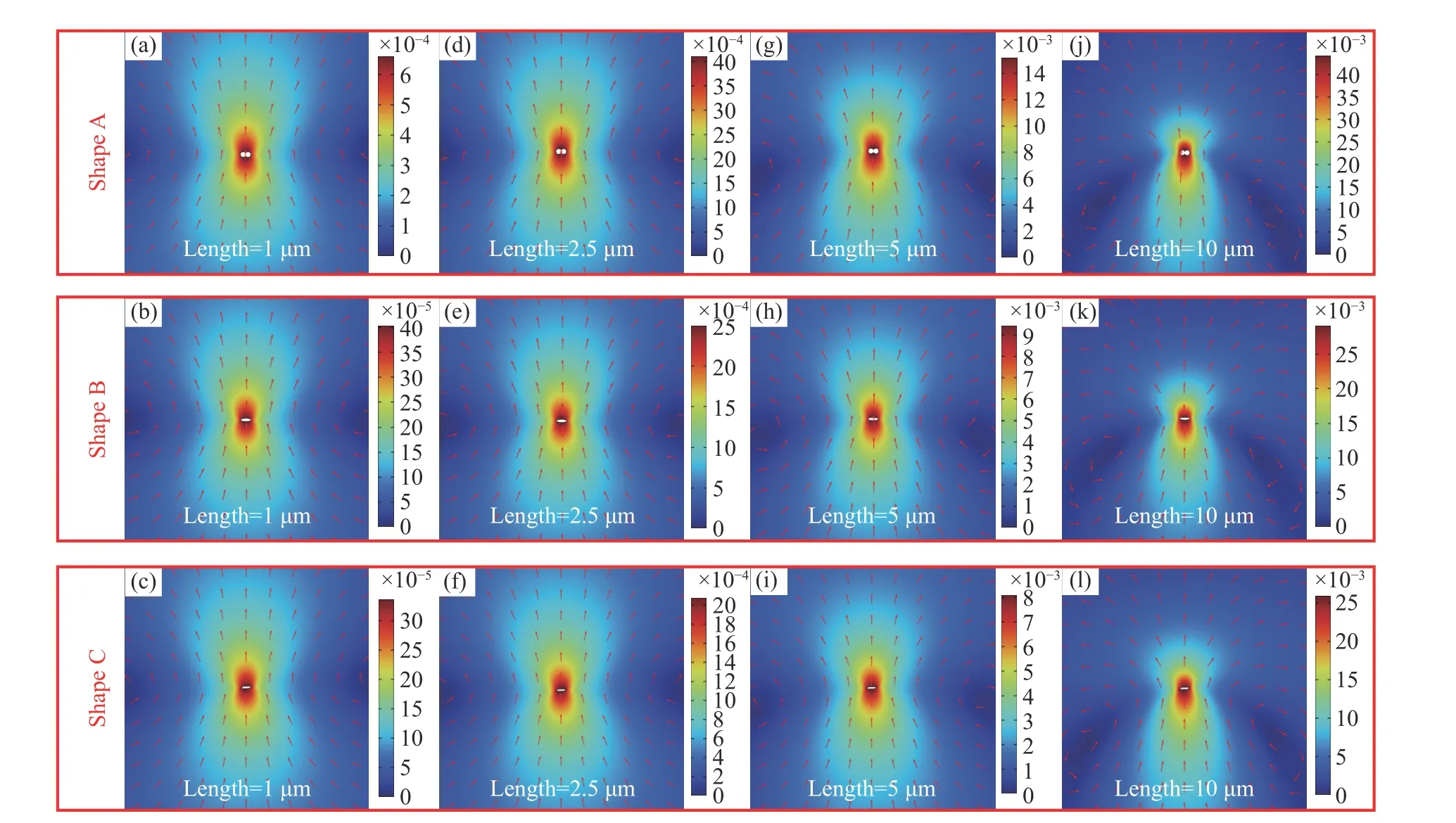
图4 G=1000超重力场下不同形状夹杂物上浮速度场云图（单位：m·s–1）Fig.4 Floating velocity field cloud map of different shapes of inclusions in a G = 1000 supergravity field (Unit: m·s–1)

夹杂物上浮时会先经历一段加速过程，随后由于重力、阻力之和与浮力平衡，夹杂物进入匀速上浮阶段. 不同形状夹杂物的上浮速度不同，本文在夹杂物长度dl相等的基础下，采用形态比和当量直径分别描述颗粒形状对夹杂物的上浮速度的影响. 形态比即夹杂物的长度与其宽度的比，在一定程度上可以描述夹杂物的细长程度；当量直径则是与颗粒表面积相等的圆的直径，由于本模型是二维纵切面的数值模拟，因此在本文中当量直径dr定义为与颗粒截面积相等的圆的直径，公式为

式中：S为颗粒截面积，C为颗粒周长.

取不同尺寸下夹杂物上浮平衡时速度做图5（a），做表2，并将G=1000，dl=10 μm条件下的夹杂物上浮速度与表中参数作图5（b）.

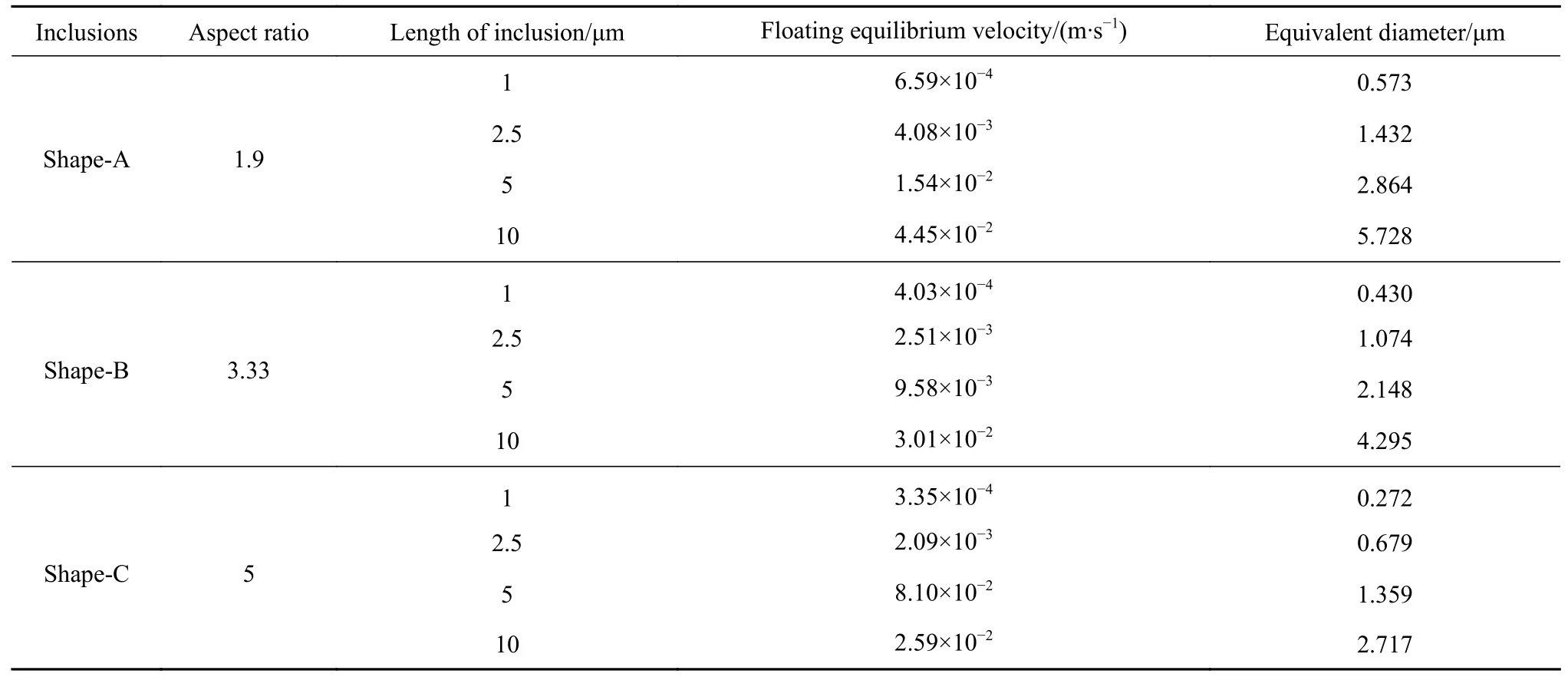
表2 不同形状夹杂物的长度、上浮平衡速度与当量直径Table 2 Length, floating equilibrium velocity, and equivalent diameter of differently shaped inclusions

图5 不同形状夹杂物的上浮平衡速度曲线和速度–形状参数关系曲线. (a) G=1000重力场中不同形状夹杂物在不同尺寸下的上浮平衡速度;(b) G=1000，dl=10 μm夹杂物形态比、上浮平衡速度与当量直径关系Fig.5 Floating equilibrium velocity curve and velocity–shape parameter relationship curve for different shapes of inclusions: (a) floating equilibrium velocity of inclusions of different shapes and sizes in a gravity field of G = 1000; (b) morphology ratio, floating equilibrium velocity, and equivalent diameter relationship of 10 μm inclusions when G = 1000

在模拟的三种夹杂物形状中，夹杂物的当量直径由大到小依次为A>B>C；上浮平衡速度由大到小依次为A>B>C；形态比由大到小依次为C>B>A. 夹杂物形态比数值越大，其形状越细长，上浮速度也越慢；相同dl下，A、B、C三种夹杂物的当量直径越大，形态比就越小，当量直径大的夹杂物通常可以在上浮阻力近似的情况下获得更多的体积，也就能受到更大的浮力以提升上浮速度.文献[24–25]中通过超重力法去除金属溶体中的杂质，304钢在80g的超重力下处理15 min，总氧质量分数最低为0.0093%，去除率为38%；718合金在210g的超重力下处理10 min，总氧和总氮的质量分数分别为0.00087%和0.00341%，去除率分别是74.7%和74.4%. 结果表明，夹杂物的数量密度与平均尺寸沿超重力的方向呈梯度分布. 也就是说，若超重力系数及上浮时间都不变，尺寸较大的夹杂物上浮距离更长，上浮速度更快，这与模拟的结果相吻合.

2.2 夹杂物形状对上浮行为影响分析

为研究非球形夹杂物在钢液中的运动行为，将A形状夹杂物以0°（水平）、45°（倾斜）、90°（垂直）的初始角度开始上浮，如图6（a）、（b）、（c）所示，并解除刚体运动约束，允许夹杂物在钢液中自由运动. 模拟了dl=1、10、20 μm的A形状夹杂物在G=1000的重力场下的上浮过程，并将上浮至80dl时夹杂物周围流场图像作图6，取0～80dl区间内夹杂物的速度作图7. 当夹杂物长度在1 μm时，夹杂物并未出现明显的旋转行为，随着长度的提升，在dl=10 μm时，初始角度为45°及90°的夹杂物发生旋转行为，并最终稳定在0°继续上浮.

图6 G=1000超重力场下不同尺寸A形状夹杂物的上浮行为速度场云图（单位：m·s–1）Fig.6 Velocity field clouds of the floating behavior of A-shaped inclusions of different sizes under a G = 1000 supergravity field (Unit: m·s–1)

图7 G=1000超重力场下不同尺寸A形状夹杂物的上浮速度变化曲线. (a) dl=10和20 μm时上浮速度与上浮距离/夹杂物长度关系曲线; (b) dl=1 μm时上浮速度与上浮距离/夹杂物长度关系曲线Fig.7 Variation curve of the floating velocity of differently sized A-shaped inclusions under a G = 1000 super gravity field: (a) floating velocity versus floating distance divided by inclusion length for inclusions with lengths of 10 and 20 µm; (b) floating velocity versus floating distance divided by inclusion length for inclusions with lengths of 1 µm

dl=1 μm夹杂物没有出现明显的旋转迹象，此时夹杂物的上浮平衡速度存在差异，以垂直姿态上浮的平衡速度最快、45°时次之，水平上浮速度最慢；垂直与水平的上浮速度差距约为5%.

dl=10、20 μm的夹杂物在初始角度为45°、90°时出现了旋转行为. 初始角度为90°的夹杂物首先以垂直姿态进行加速上浮，当达到平衡速度后开始逐渐旋转，整个旋转行为持续到夹杂物呈水平姿态上浮后停止，上浮速度随夹杂物的旋转产生变化，如图7（a）所示. 初始角度为45°的夹杂物自上浮开始阶段就存在旋转行为，当上浮速度达到平衡段时已基本完成旋转，因此上浮速度变化曲线与水平上浮时基本一致.

夹杂物的尺寸增大，旋转过程发生越快.dl=10 μm夹杂物以90°初始角度完成旋转需要上浮约50～60dl距离，而dl=20 μm完成同样的旋转行为只需要30～40dl距离，旋转整个用时约0.004 s.

垂直上浮时受到的阻力最小，随着颗粒尺寸的提升，夹杂物上浮速度的加快，夹杂物两侧受力更易出现不均匀发生旋转行为，且垂直上浮时夹杂物的重心较高，旋转至水平后获得了最低的重心，因此最终以水平姿态稳定上浮.

颗粒雷诺数是描述流体流动状态的重要指标，使用夹杂物的当量直径及上浮平衡速度计算夹杂物在不同时间段的雷诺数，计算出的数据总结于表3. 其中，颗粒雷诺数的计算公式为：

表3 A形状夹杂物的长度、当量直径与雷诺数Table 3 Length, equivalent diameter, and Reynolds number of Ashaped inclusions

式中：dr为当量直径，u为颗粒速度，ρ为钢液密度，μ为钢液黏度.

dl=1 μm的夹杂物颗粒雷诺数远小于1，属于蠕动流区域，不会产生旋转行为；dl=10 μm夹杂物的雷诺数小于1时，上浮属于层流区，发生了旋转行为；夹杂物雷诺数大于1小于100时，夹杂物进入过渡区，同时夹杂物也发生了旋转. 由此可见，旋转行为的发生与颗粒雷诺数有关，夹杂物周围流场处于蠕动流区不发生旋转行为，而层流区和过渡区则会发生. 此外，对夹杂物形状B和夹杂物形状C进行了相同条件的模拟验证，同样出现了旋转行为，说明具有较高长宽比的夹杂物均会产生类似的上浮特征. 文献[22]中指出，夹杂物受形状影响会在上浮时会发生翻转行为，夹杂物运动取向变化会导致夹杂物受到的阻力发生改变，与模拟出的结果相类似.

2.3 重力系数对A形状夹杂物上浮行为影响分析

在实际生产中，超重力设备提供的离心力可以通过转速控制，因此讨论重力系数对夹杂物上浮行为的影响十分重要. 取dl=20 μm的A形状夹杂物分别以800g、600g、200g、50g重力系数进行模拟，该尺寸可以通过调整重力系数使夹杂物周围流场分别位于层流区以及过渡区. 初始角度分别选取90°及45°，取夹杂物周围流场作图8，取0～80dl区间内夹杂物的速度作图9. 随着重力系数的减小，夹杂物周围流场开始从过渡区逐渐移动至层流区，夹杂物均出现了旋转行为，但重力系数较小时夹杂物并未完全旋转至水平状态. 同时，初始角度对夹杂物的旋转有一定影响，45°角的夹杂物更易完成旋转过程.

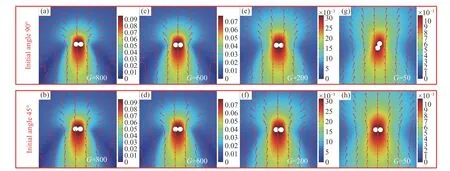
图8 dl=20 μm的A形状夹杂物在不同重力场中的上浮行为速度场云图（单位：m·s–1）Fig.8 Velocity field clouds of the floating behavior of the A-shaped inclusions with length = 20 μm in different gravity fields (Unit: m·s–1)

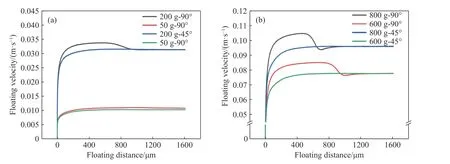
图9 dl=20 μm的A形状夹杂物在不同重力场中的上浮速度变化曲线. (a) G=200和50时上浮速度与上浮距离关系曲线; (b) G=800和600时上浮速度与上浮距离关系曲线Fig.9 Variation curve of the floating velocity of A-shaped inclusions with length of 20 μm in different gravity fields: (a) floating velocity and floating distance relationship curve when G = 200 and 50; (b) floating velocity and floating distance relationship curve when G = 800 and 600

夹杂物的在不同重力场下的上浮速度不同，但对夹杂物的周围流场及旋转行为的影响与尺寸带来的影响在一定条件下基本相同，如G=200，dl=20 μm和G=1000，dl=10 μm，二者虽夹杂物尺寸和重力系数不同，但夹杂物周围流场和运动行为基本相同.

在实际生产中，钢中夹杂物形状各不相同，若想通过超重力技术制得近零夹杂物钢，则需要让可去除范围内上浮速度最慢的夹杂物有足够的时间上浮去除. 从本研究结果可知，对于具有一定长宽比的夹杂物，上浮发生旋转的过程极快（G=1000，dl=20 μm，旋转需要约0.004 s），其绝大部分上浮时间都是以水平姿态进行上浮. 因此，在通过模型预估夹杂物离心处理时间应以水平姿态上浮时的平衡速度进行考虑. 基于此结论，以G=500、dl=1、2.5、5 μm的A、B、C形状夹杂物的水平状态上浮速度、50 cm上浮距离为基本参数，计算上浮时间于表4，用于实际工程应用装置参数的确定与设计时进行参考.

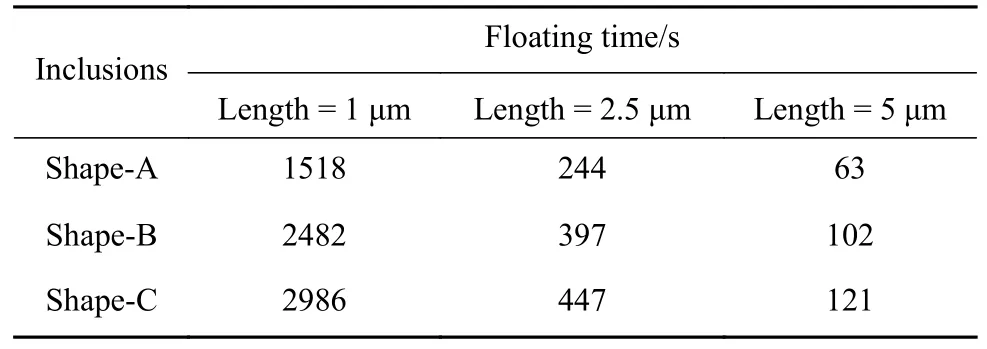
表4 G=500、dl=1、2.5、5 μm不同形状夹杂物上浮50 cm所需时间Table 4 Length, floating equilibrium velocity, and equivalent diameter of differently shaped inclusions

2.4 夹杂物取向对材料性能的影响讨论

具有较高形态比的夹杂物按相同朝向存在于在钢基体中会导致钢的性能出现各向异性[26]. 该类型的小尺寸夹杂物在钢液中可认为基本不出现旋转的行为或旋转行为发生极为缓慢，因此小尺寸的夹杂物虽易残留在钢液中，但其朝向各不相同，不会引起钢材性能出现各向异性. 对于较大尺寸的夹杂物，虽会出现旋转行为，但其上浮速度快，去除较为彻底，因此也不会导致钢材性能各向异性. 因此，超重力法去除钢中的夹杂物没有明显负面影响.