基于SPH方法的围油栏仿真研究

刘家齐　焦培刚　许云涛

摘要：为解决计算流体动力学（computational fluid dynamics，CFD）方法在模拟围油栏围控溢油时流-固耦合、水-油液体两相流中的不稳定性、计算效率差、将自由表面视为滑移壁且不考虑围油栏移动等问题，基于光滑粒子流体动力学（smoothed particle hydrodynamics，SPH）方法建立适用于围油栏围控溢油的固-液耦合、液体两相流数值模型，将5种不同裙摆结构的围油栏导入两相液体相互作用的数值仿真模型中，通过SPH代码设定数值模拟相关参数，提高计算效率，得到较精确的围油栏滞油长度与溢油失效步长。结果表明：围油栏围控溢油能力与上、下裙摆高度比及裙摆角类型有关，上裙摆高度占比越大，围油栏的滞油表现越好；前折角型围油栏的滞油表现优于前转角型围油栏；滞油长度与油品性质有关，油品的密度和黏度越小，围油栏的滞油长度越大。

关键词：SPH方法；围油栏；固-液耦合；水-油两相流；滞油长度；失效步长

中图分类号：U698.7;O359；TE 991文献标志码：A文章编号：1672-0032（2024）01-0116-08

引用格式：刘家齐，焦培刚，许云涛.基于SPH方法的围油栏仿真研究［J］.山东交通学院学报，2024，32（1）：116-123.

LIU Jiaqi， JIAO Peigang， XU Yuntao. Simulation study on oil containment boom based on SPH method［J］.Journal of Shandong Jiaotong University，2024，32（1）：116-123.

0 引言

海上开采石油和运输石油时易发生石油泄漏和溢出事故。全世界每年因航运而泄漏到海洋中的石油污染物高达200万t[1]。溢油污染海洋环境，造成海洋生物大规模死亡，给沿海地区造成巨大经济损失，且持续时间较长。如何在石油泄漏后限制其外溢，防止石油大范围扩散是海洋工程中非常重要的课题。围油栏是石油泄漏应急响应中的重要工具，可有效遏制石油扩散，防止海洋环境污染加剧[2-3]。

学者通过水槽试验研究溢油围控机制和围油栏失效情况。Brown等[4]在室外流水通道中观察油品的围控和围油栏失效案例，获得有关围油栏失效机制的数据。Amini等[5]通过试验研究围油栏失效的不稳定机制。Yang等[6]采用改进的多相光滑粒子流体动力学（smoothed particle hydrodynamics，SPH）方法模拟使用移动围油栏控制油泄漏，研究油的类型、围油栏的移动速度、裙摆角度、水波等因素对滞油效果的影响。围油栏的深度和类型是影响围油栏附近流速的主要因素。随计算机硬件、软件和数值方法的迅速发展，溢油数值模拟的应用越来越广泛。Gotoh等[7]采用亚粒子尺度（sub-particle scale，SPS）表示运动粒子半隐式（moving particle semi-implicit，MPS）模型中湍流的影响。水域溢油问题涉及水-油两相流动的自由表面，围油栏对溢油的控制涉及复杂的流-固相互作用，处理两相流动、自由表面流动及流固相互作用是数值模拟的重要任务，基于网格的传统数值方法在同时追踪固体的运动、变形及自由表面、流体界面方面存在困难。溢油数值模拟主要依赖计算流体动力学（computational fluid dynamics，CFD）軟件FLUENT和CFX，将自由表面视为滑移壁，且不考虑围油栏移动的数值结果与实际结果存在一定差距[8-10]。

本文设计4种围油栏裙摆结构，分析其对围油栏滞油长度及失效时间的影响，采用改进的SPH方法，将溢油视为非牛顿流体，采用改进的亚粒子尺度（sub-particle scale，SPS）湍流模型，建立水-油两相流模型和流-固相互作用模型，对围油栏进行仿真研究，以期提高数值模拟的精度和效率，为围油栏裙摆结构设计提供理论依据。

1 SPH方法

SPH方法是基于粒子的数值方法，最初用于天体物理学领域中天体的演化计算，主要思想是将流体连续体划分为大量的离散粒子，通过核函数对粒子进行平滑化处理获得流体的速度、压力等物理量，后逐渐应用于流体力学、物理学、材料科学等领域[11-13]，相较于传统有限体积法（finite volume method，FVM）和有限元法（finite element method，FEM），SPH方法无需网格、可处理复杂边界和变形流体、可自适应地改变粒子密度等[14-15]。

围油栏防溢油涉及复杂的水-油两相流和流-固耦合问题，SPH方法适用于处理流动的复杂边界和多相流问题。可将流体视为1组质点，每个质点都有一定的质量、速度、密度等属性。计算质点间的相互作用，得到流体的运动状态和压力分布[16-17]。建立不同的裙摆形状模型模拟围油栏的失效。

1.1 非牛顿流体

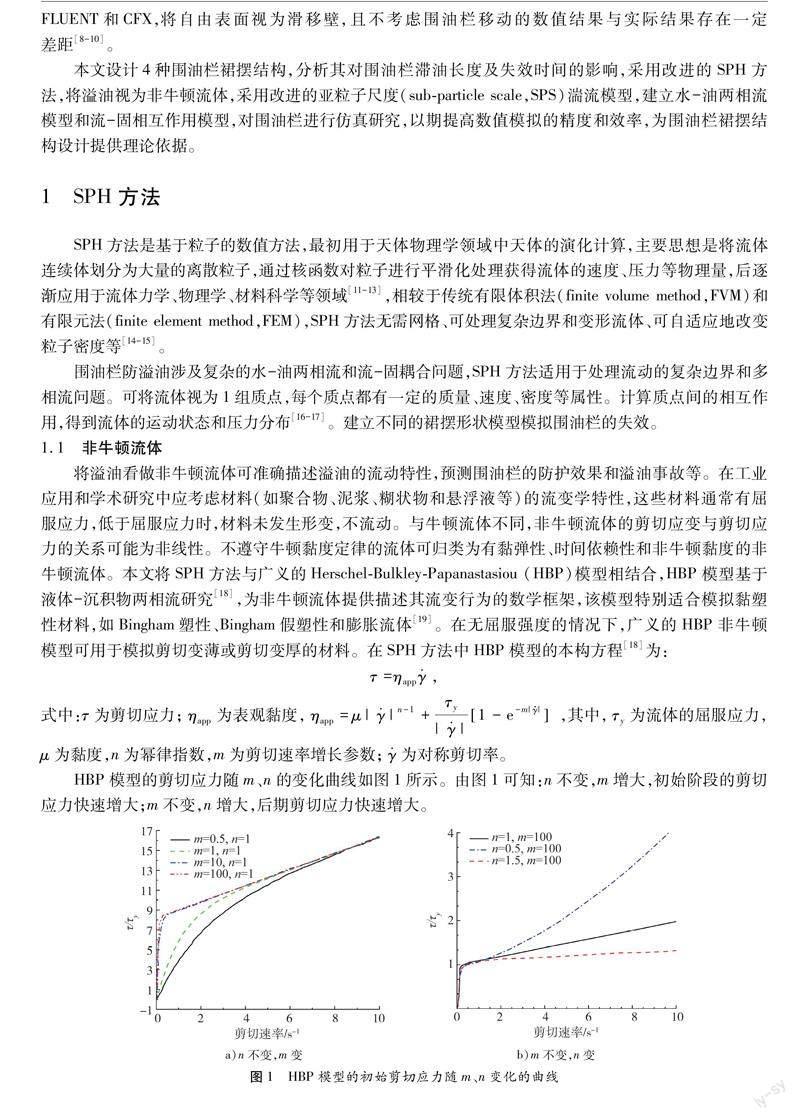
将溢油看做非牛顿流体可准确描述溢油的流动特性，预测围油栏的防护效果和溢油事故等。在工业应用和学术研究中应考虑材料（如聚合物、泥浆、糊状物和悬浮液等）的流变学特性，这些材料通常有屈服应力，低于屈服应力时，材料未发生形变，不流动。与牛顿流体不同，非牛顿流体的剪切应变与剪切应力的关系可能为非线性。不遵守牛顿黏度定律的流体可归类为有黏弹性、时间依赖性和非牛顿黏度的非牛顿流体。本文将SPH方法与广义的Herschel-Bulkley-Papanastasiou （HBP）模型相结合，HBP模型基于液体-沉积物两相流研究[18]，为非牛顿流体提供描述其流变行为的数学框架，该模型特别适合模拟黏塑性材料，如Bingham塑性、Bingham假塑性和膨胀流体[19]。在无屈服强度的情况下，广义的HBP非牛顿模型可用于模拟剪切变薄或剪切变厚的材料。在SPH方法中HBP模型的本构方程[18]为：

1.2 计算方法

SPH方法通过1组物质点或粒子离散连续介质。在流体动力学模拟中，SPH方法根据周围粒子的速度、压力等物理属性，在每个粒子位置对离散的Navier-Stokes方程进行局部积分。由基于距离的二维函数或三维函数确定这组粒子的邻近性。在每个时间步内，计算每个粒子的新速度、新压力等物理量，粒子根据更新的计算结果移动[20]。

1.2.1 SPH近似

采用基于插值函数的积分方程，将连续流体动力学的守恒定律从偏微分方程形式转化为适于基于粒子的模拟形式，给出特定点的估计值。这种插值或加权函数被称为核函数W，基本原理是用积分插值近似任何函数，积分函数[21]

2 数值模型

为验证试验效果，在数值水槽模型[6]中加入SPS湍流模型及非牛顿流体溢油。数值水槽如图2所示。水槽长19.80 m，水深2.25 m，水槽左侧设置造波器，制造一阶规则波，右侧设置消波区，围油栏在拖船的控制下以恒定水平速度vb向左移动，在垂直方向上可自由移动。

研究不同裙摆形状对围油栏拦油效果的影响，探索如何优化浮体结构，提高防溢油能力，设计4种改进裙摆固体浮子式围油栏，结构参数如表1所示。

A为未改进围油栏，B、C、D、E为改进后的围油栏。围油栏结构包括吊杆、臂架和裙摆组，裙摆分为前折角型（图3a））和前转角型（图3b）），围油栏类型如图4所示。B、D型围油栏的H1=H2，C、E型围油栏的H1=2H2。裙摆高0.75 m，裙摆角α为裙摆与竖直方向的夹角，B、C型围油栏的裙摆角均为45°。在围油栏前布置厚0.01 m，长2.00 m的薄油层。围油栏移动速度不小于0.50 m/s时，围油栏拦油失效，围油栏的临界速度[24]为0.25～0.50 m/s。

分析浮子式围油栏裙摆形状对滞油效果及失效时间的影响，主要包括不同结构围油栏在移动速度为0.30 m/s下的滞油效果和在移动速度为0.50 m/s时的失效时间。为使数值模拟结果更精确，将模拟时间30 s划分为300个步时。

3 数值模拟结果分析

采用SPH代码，对更改裙摆形状后的围油栏防溢油进行数值模拟，时间积分采用Symplectic Position Verlet数值积分格式，其优势为可在长时间积分中较好地保持能量和动量守恒，计算简单且高效。采用修正动态边界条件（modified dynamic boundary condition，mDBC）的边界处理方法，边界粒子的排列与内部粒子一致，在边界界面处设置半个粒子间距的界面。采用虚拟节点和校正的SPH算法可更准确地计算流体属性，尤其是边界角落和复杂几何形状[24]。

采用非牛頓流体对溢油进行数值建模，使模拟结果更准确，更方便观察溢油控制的物理过程。在自由曲面、移动界面和流固相互作用的广泛应用中，已证明SPH代码与改进算法的有效性[25]，可用于研究不同因素对溢油控制的影响，其他数值模拟参数如表2所示。

3.1 滞油长度

设定围油栏的移动速度为0.30 m/s，进行数值模拟的全过程中未出现临界现象。轻油、重油、水的滞油密度分别为850、950、1 000 kg/m 运动黏度分别为3.32×10-6、3.00×10-2、1.00×10-6 m2/s。波速相同、不同围油栏结构下，围油栏对重油、轻油的滞油长度如表3所示。

由表3可知：改进围油栏结构后，围油栏对重油、轻油的滞油长度均增大。重油情况下，B、C、D、E型围油栏的滞油长度比A型分别增大0.110、0.124、0.100、0.078 m；轻油情况下，B、C、D、E型围油栏的滞油长度比A型分别增大0.113、0.126、0.083、0.058 m。B、C型围油栏中，H1=2H2的围油栏的溢油长度大于H1=H2的围油栏，C型围油栏结构优于B型；D、E型围油栏的前转角越大，滞油长度越大，防溢油效果越明显，D型围油栏结构优于E型。H1=H2时，B型围油栏的滞油长度比D型大0.010 m；H1=2H2时，C型围油栏的滞油长度比E型大0.046 m，前折角型围油栏结构的滞油效果优于前转角型。5种围油栏对重油的滞油长度小于轻油，表明滞油长度与油品性质有关，油品的密度和黏度越小，围油栏的滞油长度越大。

溢油为重油时，5种围油栏结构的滞油效果如图5所示。

由图5可知：随围油栏向左侧恒速移动，溢油在围油栏左侧聚集，5种围油栏结构对溢油的聚集长度及形状不同；改进后的围油栏的滞油长度比A型围油栏大，折角型和转角型围油栏均可提高围油栏的围油性能；H1与H2之比影响围油栏的滞油效果，B、C、D、E型围油栏的滞油长度随H1的增大、H2的减小而增大，滞油效果提高；C型围油栏左侧的溢油分布更均匀，B型围油栏左侧出现溢油聚集增厚现象；D型围油栏左侧溢油分布更均匀，E型围油栏左侧出现溢油聚集增厚现象， C、D型围油栏的溢油集聚效应弱，溢油从围油栏下方逃窜的概率更小，失效的可能性更小。

3.2 失效时间

在重油、有波、围油栏速度为0.50 m/s时，A、B、C、D、E型围油栏的失效步长分别为122、155、175、148、143 步时，改进后围油栏的失效步长均增大，防溢油效果明显提高。在有波、围油栏速度为0.50 m/s时，B、C型围油栏的失效时间比A型延长33、53 步时，H1=2H2时的围油时间比H1=H2长，C型围油栏结构设计优于B型；D、E型围油栏的失效时间比A型延长26、21 步时，D型围油栏结构设计优于E型，前转角越大，防溢油时间越长，防溢油效果越明显。H1=H2时，B型围油栏的防溢油时间比D型围油栏延长7 步时；H1=2H2时，C型围油栏的滞油时间比E型围油栏延长32 步时，前折角型围油栏结构设计优于前转角型。

水流速度大于0.50 m/s时，A型围油栏最早出现石油逃逸现象，B、C、D、E型围油栏出现石油逃逸现象的时间有所增加。有波、围油栏速度为0.50 m/s时，5种围油栏的失效临界情况如图6所示。由图6可知：溢油聚集到一定程度时出现逃逸现象，相对于A型围油栏，改进后的B、C、D、E型围油栏改变了失效形式。A型围油栏失效时溢油沿围油栏裙摆下移后逃逸，改进后的围油栏是在溢油聚集到一定程度时，在溢油左侧下移到围油栏底部逃逸。受结构、运动惯性和流体力学影响，C型围油栏的溢油聚集程度大于B型，E型围油栏的溢油聚集程度大于D型，折角C型、转角E型围油栏的溢油聚集效果较好。

4 結束语

采用光滑粒子流体动力学方法对改进的围油栏防溢油过程进行数值模拟，克服基于网格的传统数值方法在同时追踪固体物体运动、变形及自由表面和流体界面时的困难，精准模拟围油栏围控溢油的过程，仿真结果更精确。与传统围油栏结构相比，改进裙摆结构的围油栏的围油效果更好。

目前的观察结果是定性分析，下一步可与试验数据对比，进一步验证数值模拟结果的准确性，研究更多影响因素对围油栏围控溢油的影响。

参考文献：

[1]周正，郑鲁，马斌.固体浮子式橡胶围油栏的产品特点及其技术局限性[J].珠江水运，2021（19）：111-113.

[2]张勤，孙永明.海上溢油围油栏研究现状[J].绿色科技，2015（4）：284-285.

[3]王姣.触目惊心的海洋污染[J].世界环境，2019（3）：55-58.

[4]BROWN H M， GOODMAN R H， AN C F， et al. Boom failure mechanisms：comparison of channel experiments with computer modelling results[J].Spill Science & Technology Bulletin， 1996， 3（4）：217-220.

[5]AMINI A， DE CESARE G， SCHLEISS A J. Velocity profiles and interface instability in a two-phase fluid：investigations using ultrasonic velocity profiler[J].Experiments inFluids， 2009， 46：683-692.

[6]YANG X F， LIU M B. Numerical modeling of oil spill containment by boom using SPH[J].Science China Physics， Mechanics and Astronomy， 20156：315-321.

[7]GOTOH H， IKARI H， YASUOKA T. Simulation of armor blocks in front of caisson breakwater by DEM-MPS hybrid model[C]//Proceedings of the Nineteenth （2009） International Offshore and Polar Engineering Conference. [S.l.]：ISOPE， 2009.

[8]AMINI A， SCHLEISS A J. Numerical modeling of oil-water multiphase flow contained by an oil spill barrier[J].Engineering Applications of Computational Fluid Mechanics， 2009， 3（2）：207-219.

[9]CHENGN. Numerical simulation of oil-boom failure with CFX 4. 3[J].Journal of Beijing University of Chemical Technology（Natural Science Edition）， 2002， 29（5）：25-29.

[10]FENGX， WU W Q， WU W F. Numerical simulation technology of oil containment by boom[J].Procedia Environmental Sciences， 2018：40-47.

[11]杨秋足， 徐绯， 王璐， 等. 一种基于黎曼解处理大密度比多相流 SPH 的改进算法[J].力学学报， 2019， 51（3）：730-742.

[12]杨彩虹，管延敏，康庄，等. SPS湍流模型在SPH模拟黏性流动问题中的应用[J].华中科技大学学报（自然科学版），2024，52（1）：59-65.

[13]VIOLEAU D， BUVAT C， ABED-MERAIM K， et al. Numerical modelling of boom and oil spill with SPH[J].Coast Engineering， 2007， 54（12）：895-913.

[14]LUCY L B. A numerical approach to the testing of the fission hypothesis[J].The Astronomical Journal， 1977， 82（12）：1013-1024.

[15]GINGOLD R A， MONAGHAN J J. Smoothed particle hydrodynamics：theory and application to non-spherical stars[J].Monthly Notices of the Royal Astronomical Society， 1977， 181：375-389.

[16]YANG X F， PENG S L， LIU M B， et al. Numerical simulation of ballast water by SPH method[J].International Journal of Computational Methods， 2012， 9（1）：1240002.

[17]沈雁鸣，陈坚强.SPH方法对气液两相流自由界面运动的追踪模拟[J].空气动力学学报，2012，30（2）：157-161.

[18]FOURTAKAS G， ROGERS B D. Modelling multi-phase liquid-sediment scour and resuspension induced by rapid flows using smoothed particle hydrodynamics （SPH） accelerated with a graphics processing unit （GPU）[J].Advances in Water Resources，2016，92：186-199.

[19]乔成， 潘华利， 欧国强. 两相光滑粒子流体动力学方法在动床溃坝问题中的应用[J].中国科学院大学学报， 2017， 34（5）：625-632.

[20]TAGLIAFIERRO B， MANCINI S， ROPERO-GIRALDA P， et al. Performance assessment of a planing hull using the smoothed particle hydrodynamics method[J].Journal of Marine Science and Engineering， 2029（3）：244-261.

[21]LIU G R， LIU M B. Smoothed particle hydrodynamics[M].[S.l.]：World Scientific Publishing，2003.

[22]LIND S J， ROGERS B D， STANSBY P K. Review of smoothed particle hydrodynamics：towards converged Lagrangian flow modelling[J].Proceedings of theRoyal Society A：Mathematical， Physical and Engineering， 2020， 476（2241）：20190801.

[23]MONAGHAN J J. Simulating free surface flows with SPH[J].Journal of Computational Physics， 1994， 110（2）：399-406.

[24]CORMACK D. Response to marine oil pollution[M].[S.l.]：Springer Science & Business Media， 1999.

[25]SHAO J R， LI H Q， LIU G R， et al. An improved SPH method for modeling liquid sloshing dynamics[J].Computers Structures， 2012，100：18-26.

Simulation study on oil containment boom based on SPH method

LIU Jiaqi， JIAO Peigang*， XU Yuntao

Abstract：A numerical model for solid-liquid coupling and two-phase flow is developed based on the smoothed particle hydrodynamics （SPH） method to address issues such as flow-solid coupling， instability in two-phase flow of water and oil， poor computational efficiency， and the assumption of a slip wall with no consideration of oil barrier movement in traditional computational fluid dynamics （CFD） methods for simulating oil spill containment using oil booms. Five different skirt structures of oil booms are incorporated into the numerical simulation model of two-phase liquid interaction. By setting relevant parameters in the SPH code， the computational efficiency is improved， and accurate values for the length of oil retention by the oil boom and the oil spill failure step were obtained. The results show that the effectiveness of oil spill containment by the oil boom depends on the ratio of upper and lower skirt heights and the type of skirt angle. A higher ratio of upper skirt height leads to better oil retention performance. The oil boom with a forward folding skirt angle performs better than the one with a forward turning skirt angle. The length of oil retention is influenced by the properties of the oil; smaller density and viscosity of the oil result in a greater length of oil retention.

Keywords：SPH method; oil boom; solid-liquid coupling; water-oil two-phase flow; length of oil retention; failure step

（責任编辑：王惠）

收稿日期：2023-04-20

基金项目：山东省重点研发计划项目（2019GNC106032）；山东交通学院研究生科技创新项目（2022YK085）

第一作者简介：刘家齐（1998—），男，山东临沂人，硕士研究生，主要研究方向为智能制造，E-mail：499610733@qq.com。

*通信作者简介：焦培刚（1974—），男，山东聊城人，教授，工学博士，硕士研究生导师，主要研究方向为机械工程、虚拟现实、光滑粒子流体动力学，E-mail：jiaopeigang@126.com。