均载组合式小轮径货车转向架车轮型面优化设计研究
2024-04-11曹玉峰张卫华祁亚运池茂儒王洪昆
曹玉峰, 张卫华, 祁亚运,3, 池茂儒, 王洪昆
(1.西南交通大学 轨道交通运载系统全国重点实验室, 成都 610031; 2.国能铁路装备有限责任公司,北京 100011; 3.重庆交通大学 机电与车辆工程学院,重庆 400074)
由于铁路运输具有环保节能和安全可靠的特点,驼背运输是将长距离公路运输转化为铁路运输,能够有效减少碳排放。开展铁路驮背运输是实现“门到门”运输的最好方式之一,能够有效实现公铁联运的快速转换[1-2]。开展驮背运输符合我国节能减排和货运改革的需求,同时由于我国铁路现有条件符合开展驮背运输的条件[3]。百分百低地板面驮背车对站场配套装备要求不高,仅需要硬化地面和公路货车与驮背车连接渡板,较低的地板面设计使得公路货车可以通过渡板直接开上开下驮背车,实现公路货车的快速装卸作业,车辆运用可靠性较高,丰富了我国驮背运输的发展模式。驮背车的关键技术在于小轮径转向架技术,典型的小轮径转向架如图1所示。但小轮径转向架磨耗主要集中在踏面区域和轮缘根部区域。随着磨耗增大,轮轨接触关系进一步恶化。而车轮磨耗使得车轮镟修里程缩短,而小轮径转向架由于半径较小,其车轮磨耗限值也较小,需要进一步通过型面设计减小车轮磨耗[4]。

图1 小轮径货车转向架Fig.1 Small diameter wheelfreight wagon
铁路货车车轮磨耗问题长期以来备受关注,很多学者开展了重载货车车轮磨耗的研究。崔大宾等[5]通过建立重载货车车辆模型和型面优化的方法减小磨耗。王璞等[6]利用UM动力学软件,对重载货车车轮磨耗进行预测。李亨利等[7]通过建立重载货车动力学模型,探究了重载货车车轮磨耗对车辆动力学性能的演变规律的影响。丁军君等[8]通过建立半Hertz接触模型和车辆动力学模型,对重载货车车轮磨耗展开预测。李春胜等[9]建立了重载货车模型,探讨了一系悬挂系统对其运行性能的影响。杨春雷等[10]通过采用数值方法建立重载货车车辆动力学模型,并对曲线通过性能进行分析。以上学者对重载货车车轮型面磨耗开展相关预测和动力学研究,而车轮磨耗可以通过型面优化进行控制。
目前对轨道车辆型面优化,有大量的学者进行研究。Choi等[11]利用对小曲线上的轮缘磨耗和表面接触疲劳为优化目标,进行型面优化设计。Lin等[12]利用NURBS曲线设计了地铁车辆薄轮缘型面,建立地铁车辆动力模型对型面进行评估。Qi等[13]提出了基于高斯函数修正的钢轨型面优化设计方法。Shen等[14]利用轮轨接触角反向设计车轮型面。Polach[15]提出了以共形接触为目标的车轮型面设计方法,干锋等[16]利用反向设计的方法对高速动车组型面进行设计。Qi等[17-18]利用了RSFT(rotary-scaling fine-tuning)型面设计方法对地铁车轮型面和动车组车轮型面进行优化设计,提升了车辆动力学性能并减小磨耗。以上研究都是针对重载货车或地铁车辆的相关型面设计研究,但针对小轮径低地板驮背车车轮型面优化的研究目前还尚未研究,需要进一步提升小轮径转向架的服役性能。
本文通过首先建立小轮径低地板驮背车动力学模型,然后以减小轮轨接触应力为优化目标,利用轮径差反向设计法设计车轮型面,最后利用动力学模型和磨耗模型对优化前后型面的动力学性能和磨耗特性进行对比分析。
1 均载组合式小轮径驮背车动力学模型建立
在建立该车模型时作出如下假定:①对动力学性能影响不大的零部件将其质量折合到与其相邻或有依附关系的大部件上;②轮对、侧架、摇枕和车体等部件的柔度比悬挂系统的柔度要小得多,均视为刚体,即忽略各部件的弹性变形;③不考虑车辆牵引工况和相邻车的影响,即只考虑单节车辆模型。根据计算要求,采用SIMPACK程序,进行该车动力学系统的建模和计算, 动力学模型考虑1个车体、2个构架、8个侧架、8个轮对和16个轴箱共计35个刚体,车体、构架、侧架和轮对均考虑纵向移动、横移、浮沉、侧滚、点头和摇头6个自由度,轴箱为点头1个自由度,全车共计130个自由度,动力学模型如图2所示。采用TB/T 449—2003《机车车辆车轮轮缘踏面外形》中规定的LM型车轮踏面[19]。轮对内侧距为1 353 mm,钢轨型面采用60 kg/m钢轨型面。
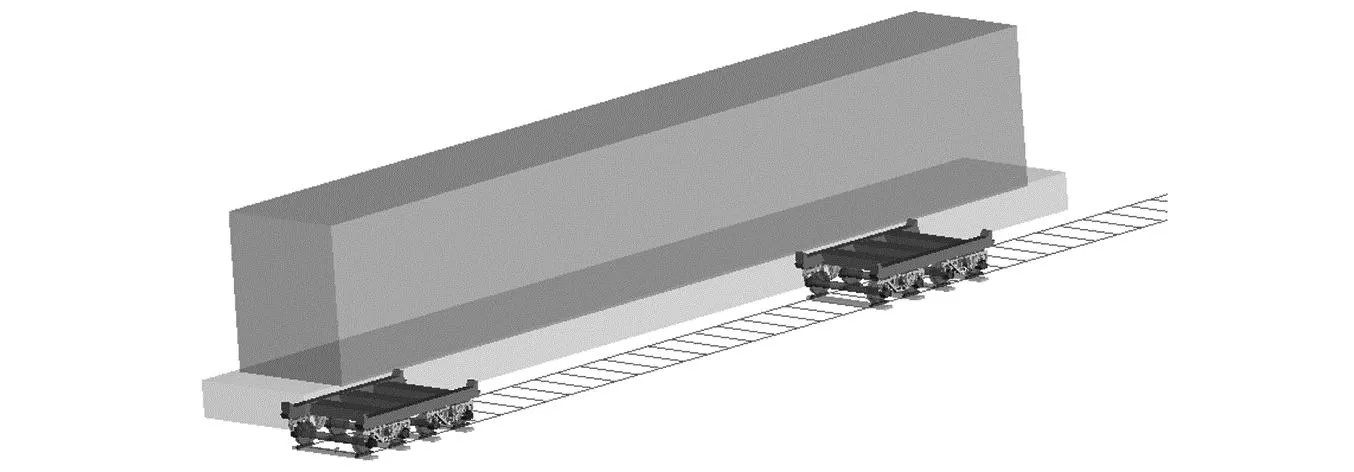
图2 车辆动力学模型Fig.2 Vehicle dynamics model
车辆的动力学方程可写成如下一般形式
(1)
式中:X为130维向量,表征系统模型的130个自由度;M为系统的惯性矩阵;F为非线性力函数向量,包括系统的弹簧阻尼力、轮轨力、离心力等;α为表征系统变化参数的向量;f(t)为系统的激扰。
模型中考虑了悬挂系统的非线性,包括各种间隙、止档、斜楔减振器、心盘及旁承的摩擦力和力矩等。其中车体与转向架之间的连接采用心盘和常接触双作用式弹性滚子旁承联合承载方式。心盘除起连接和传递垂直载荷外,还要传递纵向力和横向力,并提供车体和转向架之间的部分回转摩擦力矩。旁承为双作用弹性旁承,上下旁承始终接触,承担部分车体载荷,并提供一部分回转摩擦力矩。另外,旁承滚子与上旁承面有间隙。旁承的摩擦力矩可通过旁承刚度和预压缩量以及磨耗板的摩擦因数来进行调整。
对于心盘的回转摩擦力矩的计算,由于心盘销的直径与心盘的直径相比要小得多,可忽略其影响。因此,心盘的回转摩擦力矩的计算公式为
(2)
式中:Pc为心盘的承载;A为心盘面积;r为心盘半径;μc为心盘面摩擦因数。
对于旁承的回转摩擦力矩的计算,需考虑滚子间隙的影响,其具体算式为
(3)
式中:Ps为旁承的承载;kz为旁承的垂向刚度;Δc为旁承滚子间隙;μs为旁承面摩擦因数;ds为旁承距转向架中心距离。
由式(3)可见,采用双作用弹性旁承,当间隙压死后,摩擦力矩不会因接触刚度的增大而进一步加大,有效限制了摩擦力矩的过度增大以保证曲线通过能力。转向架侧架与摇枕间的垂向刚度和阻尼、横向刚度和阻尼均由钢弹簧和斜楔摩擦减振器提供。
2 车轮型面优化设计
由于踏面外形有部分区段不会与轨面相接触,用轮径差进行型面反向设计时,踏面不接触区域将无法进行设计,因此需要与参考型面相结合才能组成完整的车轮型面外形。也就是说反向设计出的型面由参考型面、设计的型面和二者之间的过渡段组成,如图3所示。在不同设计参数下过渡段的位置不固定,需要根据设计的型面的大小进行调整。
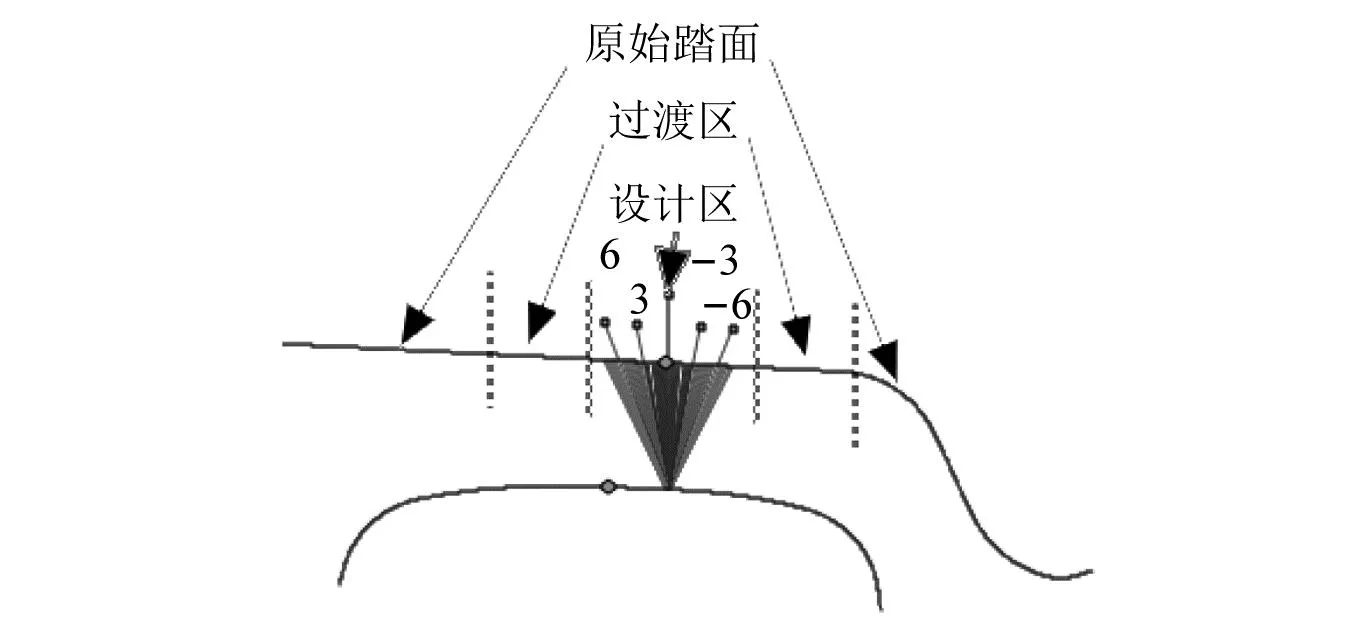
图3 车轮型面外形区域划分Fig.3 Division of wheel profile areas
为了得到较好的型面设计方法,将踏面反向设计转化为一个优化问题。设给定的踏面外形为fD,w(x),设计的踏面外形为fD,w(x),则设计误差函数为
Δfw(x)=fw(x)-fD,w(x),xmin≤x≤xmax
(4)
优化的目标函数可写成
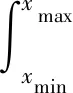
(5)
(6)
令η为给定的轮径差变化量ΔR(s)在左右踏面中的分配比例,即
(7)
由于轮对横移是一个连续的过程,且轮对踏面与轨面接触时沿轨面切线方向,则从s-Δs移动至s时ΔRL(s)和ΔRR(s)可表示为
(8)
点pL,s和pR,s的斜率分别为KR(xL,s)和KR(xR,s),点pL,s-Δs和pR,s-Δs的斜率分别为KR(xL,s-Δs)和KR(xR,s-Δs)。
在实际踏面反向设计时,需采用循环迭代的数值计算方法。计算过程为:首先在一定的给定轮对横移量s、横移步长Δs和参数ξ下,以给定轮轨初始接触点位置为起点,按照该轮对横移量s下的轮径差的要求得到此时的踏面外形点;然后依次循环迭代轮对横移量s,得到设计的踏面外形;最后调整参数ξ以获得最优的踏面外形。
轮轨接触应力计算结果如图4所示,随着轮径的减小,轮轨接触应力增大;随着轴重的减小,轮轨接触应力减小。针对LM踏面,把轮径从840 mm减小到500 mm后,即使把轴重从25 t降低到21 t,如图4(a)所示,轮轨接触应力仍然比原车状态(D=840 mm,P=25 t)大;因此需要对小车轮进行踏面优化设计,来降低轮轨接触应力。
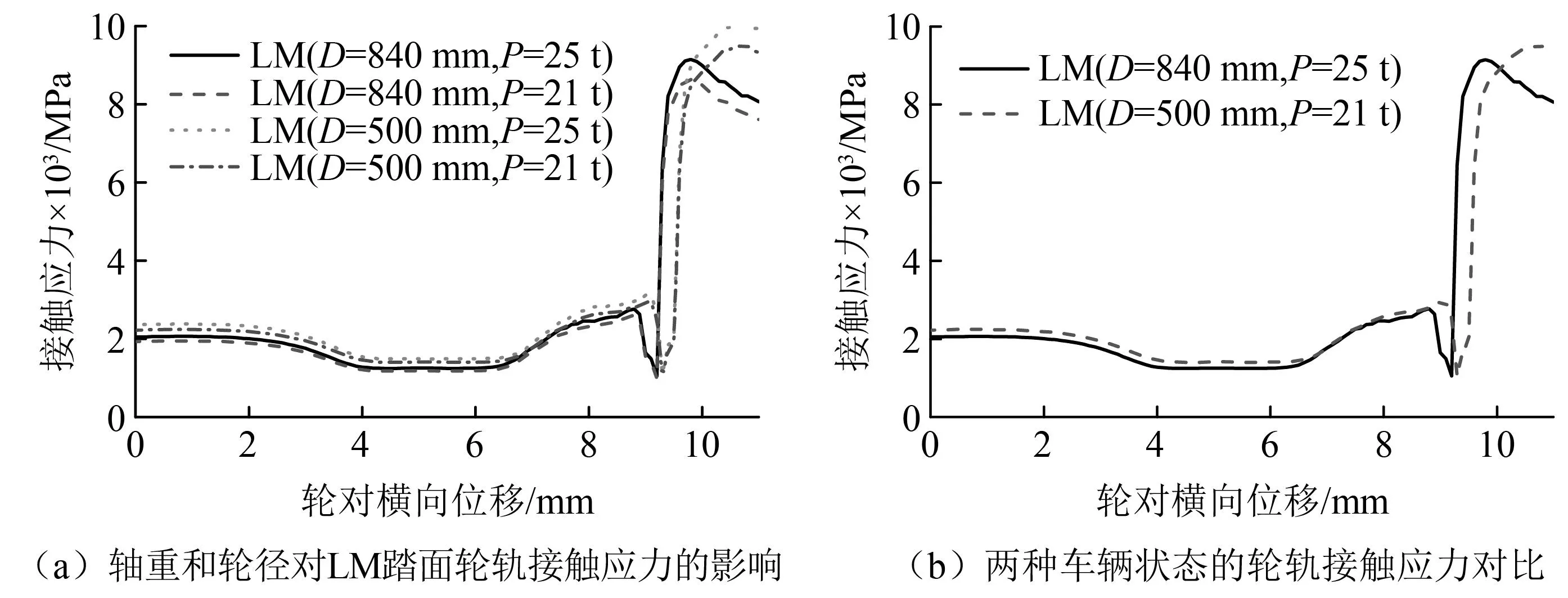
图4 轮轨接触应力对比分析Fig.4 Comparative analysis of wheel-rail contact stresses
以轮轨接触应力为目标函数,优化设计的车轮型面命名为LMG,其车轮型面如图5所示。经过优化设计的踏面LMG(D=500 mm,P=21 t)确实比LM(D=840 mm,P=25 t)的轮轨接触应力小,如图6(a)所示。优化型面LMG与原型面LM的轮轨接触关系(等效锥度和重力刚度)存在较大区别,如图6(b)和图6(c)所示,可以看出优化后型面有效减小了等效锥度和接触角差,下一步需要对LMG踏面的动力学性能展开计算分析。
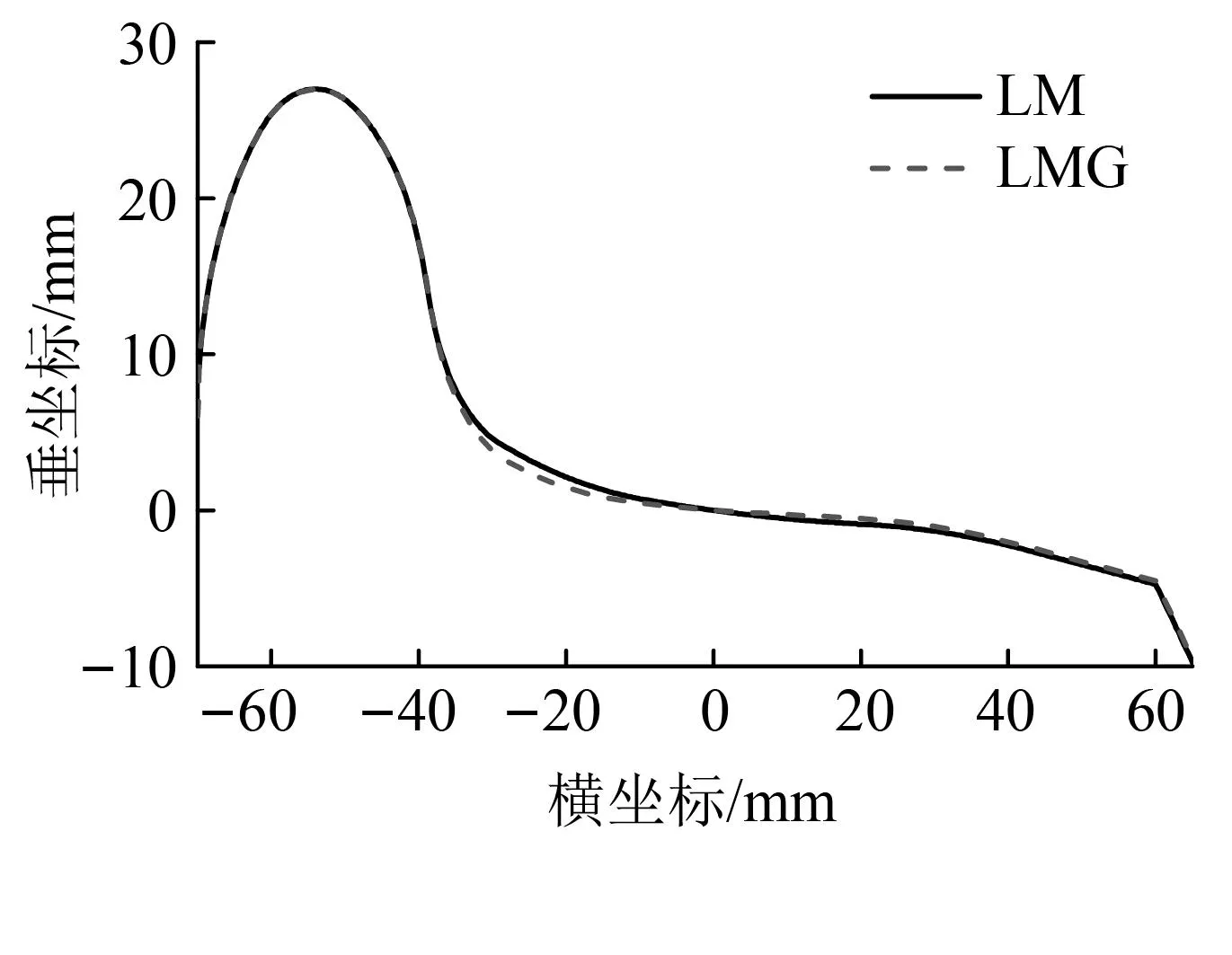
图5 优化型面LMG与型面LM的对比Fig.5 Comparison of optimized profile LMG with LM profile
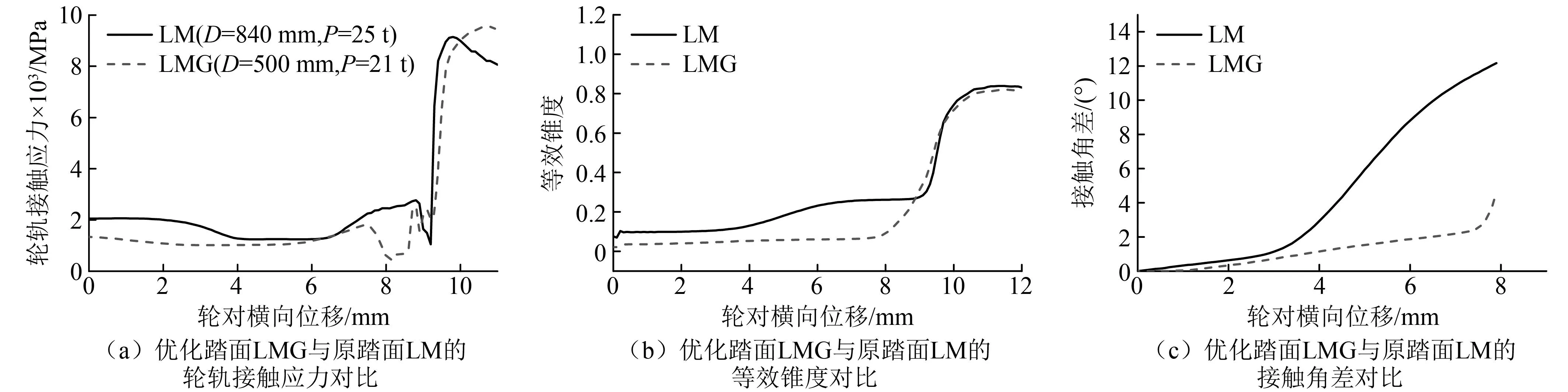
图6 优化前后轮轨参数对比Fig.6 Comparison of wheel rail parameters before and after optimization
3 优化前后动力性能分析
3.1 运行稳定性
运动稳定性是研究车辆在一定速度下运行时各部件的运动状态是否收敛,即判定车辆系统的运动是否稳定。车辆在正常运行速度下要避免出现蛇行失稳现象,这就要求车辆系统具有高于其构造速度一定裕量的蛇行失稳临界速度。对于本次计算车辆的蛇行失稳临界速度,要求高于其设计速度70 km/h,并且应具有足够的余量。在计算转向架的蛇行失稳临界速度时,先让低地板驮背车在一段美国5级线路谱为激扰的直线轨道上运行,然后让车辆再在一段理想光滑轨道上运行,看该车各部件的运动能否趋于平衡位置从而确定该车的蛇行失稳临界速度。
根据该方法计算出的小车轮低地板驮背车的临界速度如图7所示,根据计算结果可得到以下规律:随着等效锥度的增加,临界速度逐渐降低,由于LMG型面的等效锥度较小,LMG的等效锥度为0.05,LM的等效锥度为0.1, LM磨耗后型面的等效锥度为0.5。所以LMG型面的临界速度最高,空车临界速度为196 km/h,较LM型面提高23.3%,重车临界速度为209 km/h,较LM型面增大17.54%。LM型面磨耗到后期(等效锥度达到0.5),空车临界速度为96 km/h,重车临界速度为115 km/h。
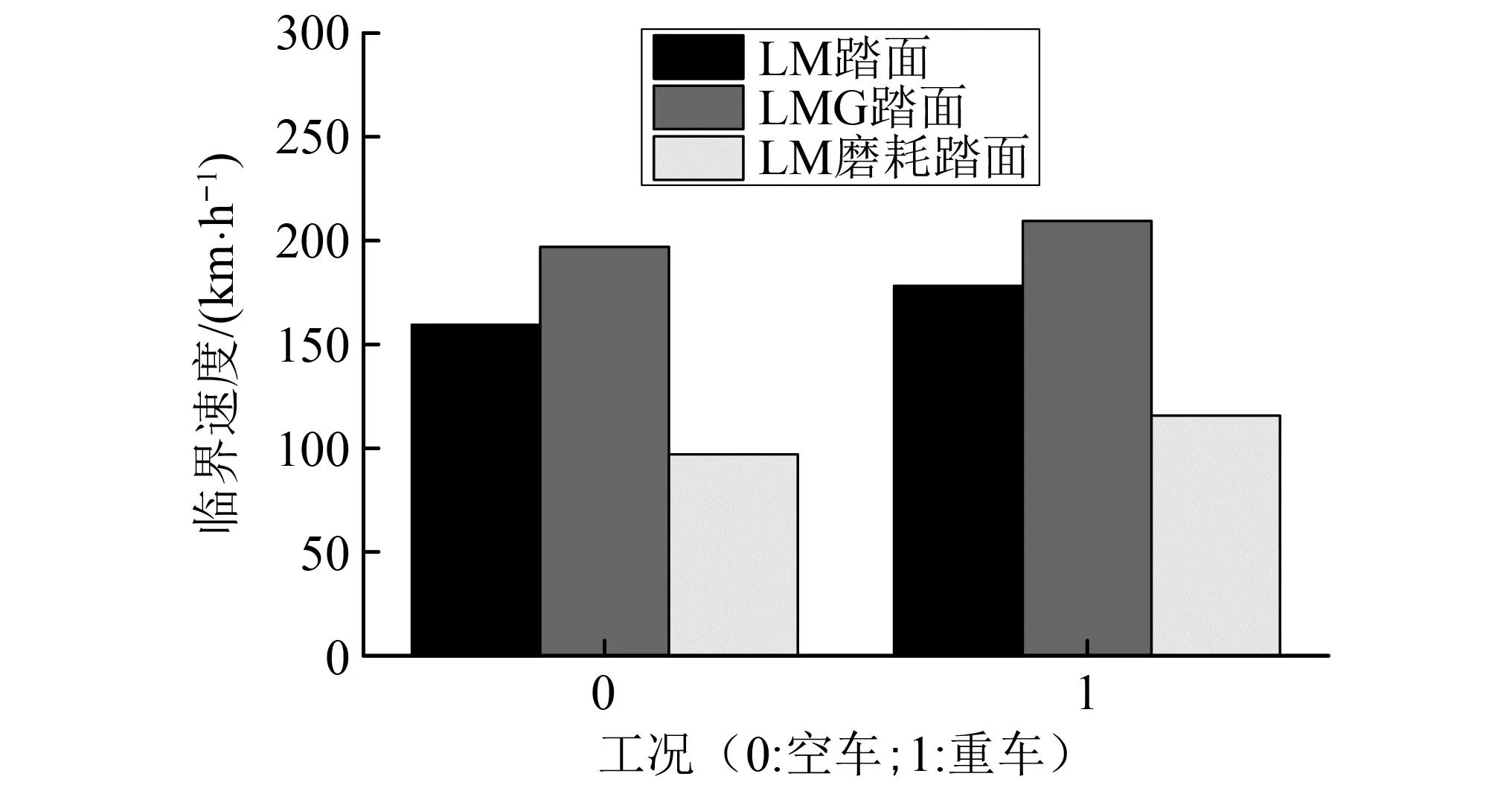
图7 不同型面空重车稳定性分析Fig.7 Stability analysis of empty and heavy vehicles with different types of wheelprofile
3.2 平稳性分析
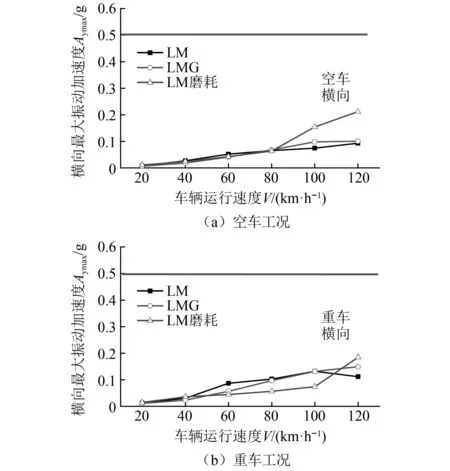
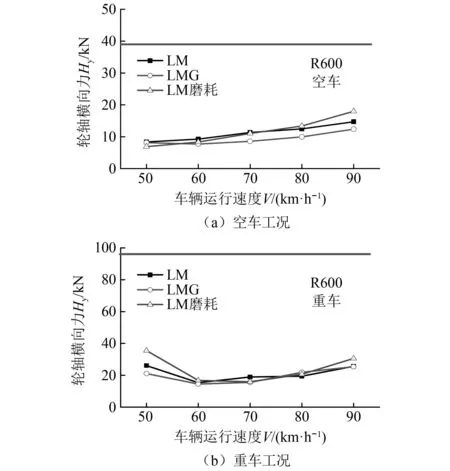
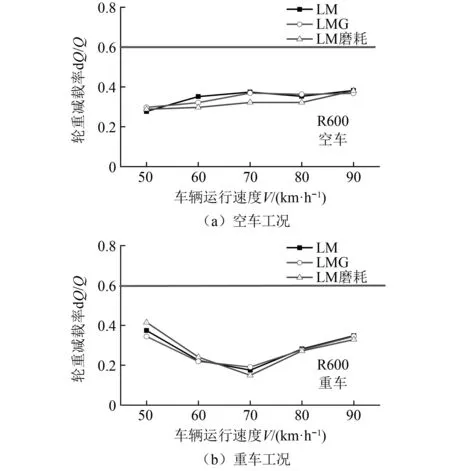
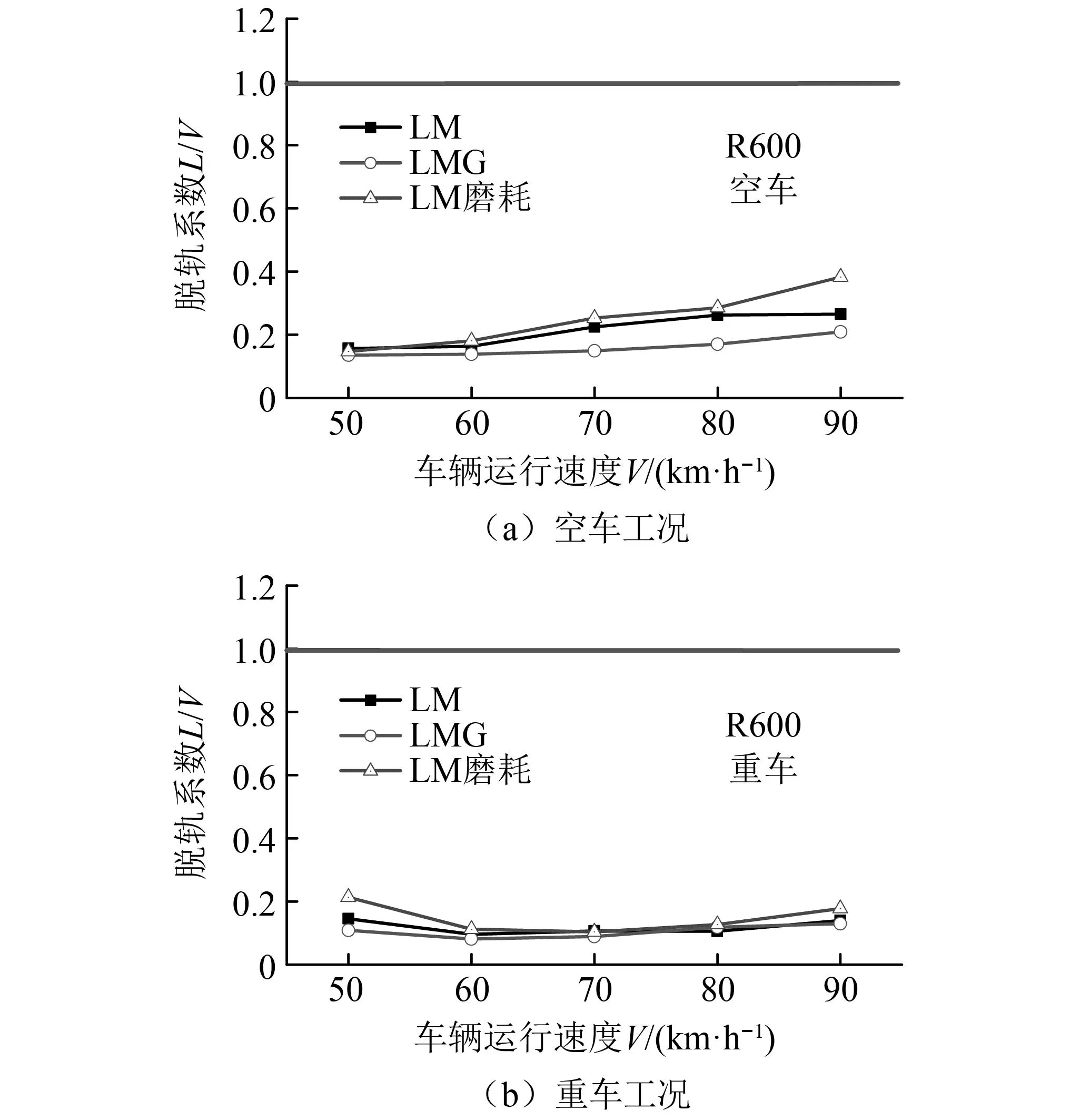
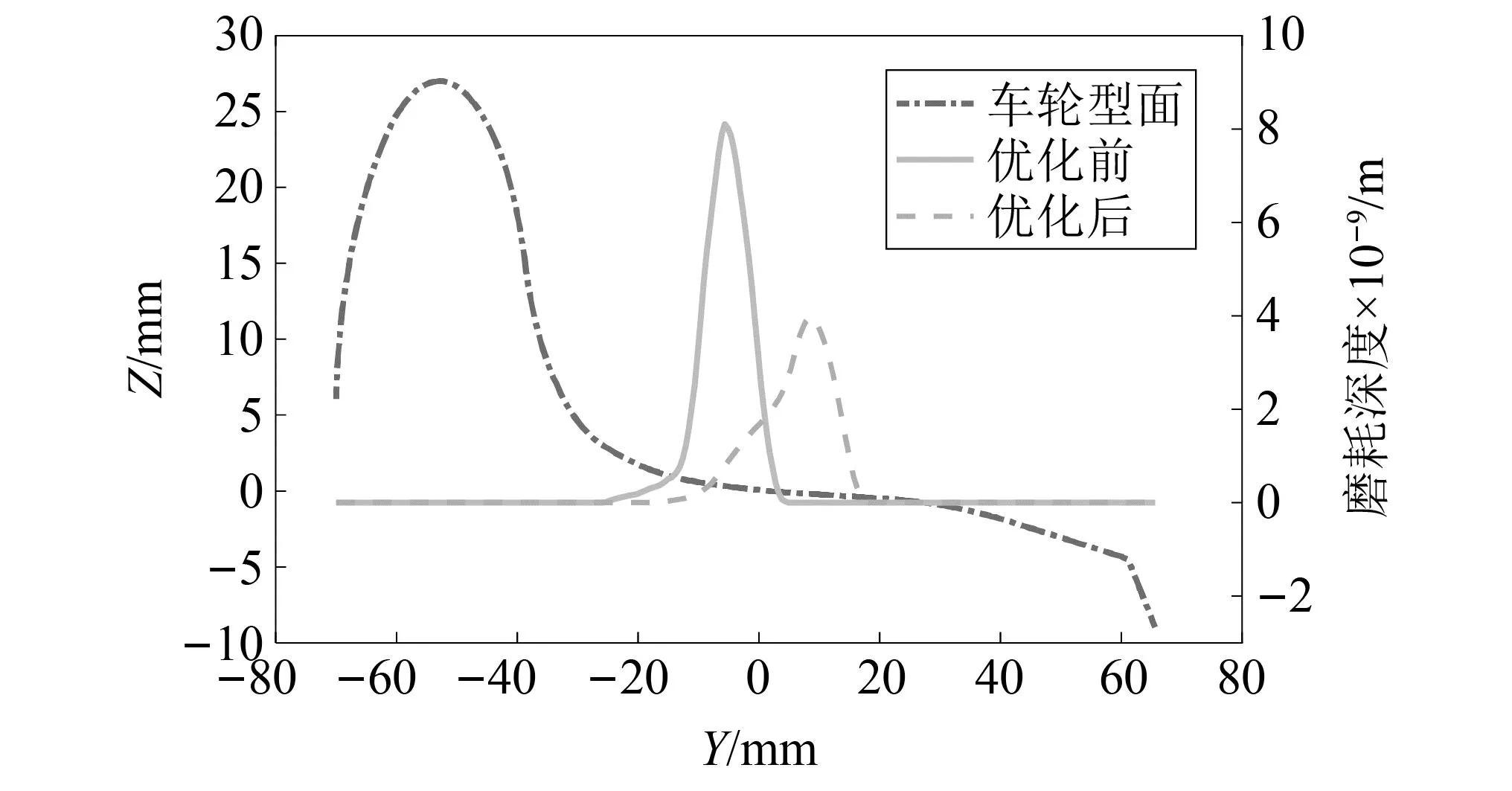
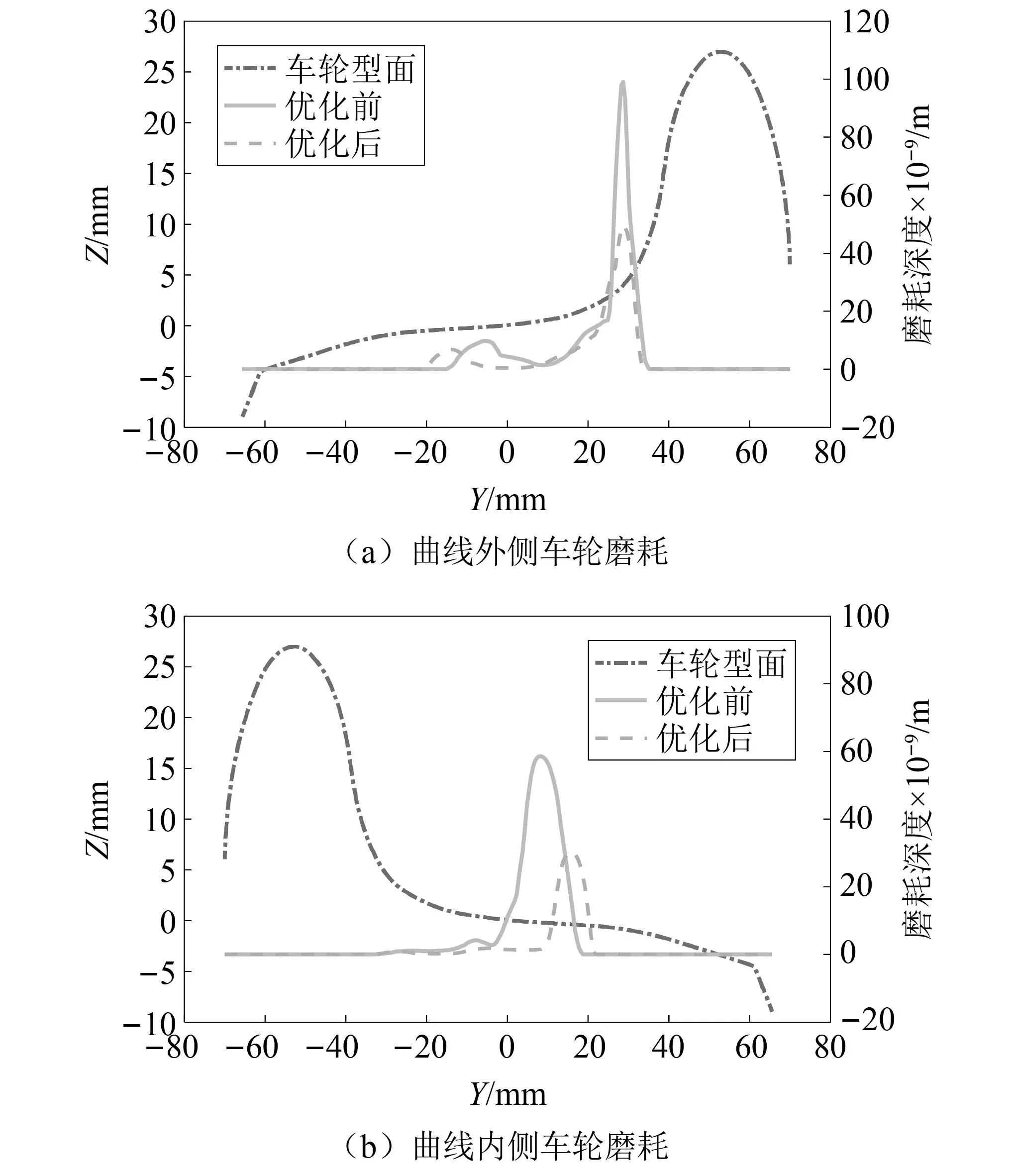
运行平稳性方面,根据GB/T5599—2019《机车车辆动力学性能评定及试验鉴定规范》规定[20],运行平稳性(确保运送货物的完整性)分别按平稳性指标、最大振动加速度评定。(1)平稳性指标:W<3.5(优),3.5 计算车辆系统的运行平稳性时,采用美国5级线路谱作为激扰,计算的速度级别为20~120 km/h。图8~图9是小轮径驮背车在20~120 km/h的速度内的平稳性指标。从图8、图9可以看出,随着运行速度的提升,横向平稳性指标、横向振动加速度均呈增大趋势;在80 km/h速度内,3种踏面的平稳性和振动加速度差别不大;平稳性都能达到GB/T 5599—1985《铁道车辆动力学性能评定》规定的优秀等级标准,振动加速度都没有超过GB/T 5599—1985《铁道车辆动力学性能评定》规定的限度值。当运行速度高于80 km/h后,LM磨耗型面的平稳性和振动加速度突然增大(主要是因稳定性不足造成的)。 图8 三种车轮型面横向平稳性的对比Fig.8 Lateral ride index of the three wheel profiles 图9 3种车轮型面横向振动加速度对比Fig.9 Comparison of lateral vibration acceleration of three wheel profiles 曲线通过运行安全性主要包括脱轨系数,轮重减载率和横向力,具体限值如下。 (1)脱轨系数Q/P 第一限度 第二限度 式中:Q为车轮作用于钢轨上的横向力;P为车轮作用于钢轨上的垂向力。 (2)轮重减载率ΔP/P 第一限度 第二限度 (3)横向力 轮轨横向力允许限度采用以下标准。 道钉拔起,道钉应力为弹性极限时的限度 Q≤19+0.3Pst 轮轴横向力允许限度采用以下标准 (9) 式中,Pst1、Pst2为左右车轮静载荷(轮重)。 该车在直线和曲线轨道上运行时,轮轴横向力的限度值根据上面公式可计算如下 空车 Q=23.68 kN,H=26.00 kN 重车 Q=33.79 kN,H=54.66 kN 图10~图11分别是小轮径低地板驮背车以50~90 km/h的速度通过R600曲线时的安全性指标。通过对比可以看出:当低速通过R145的小半径曲线时,大锥度踏面的曲线通过性能总体趋势略优于小锥度踏面;当高速通过R600的较大半径曲线时,小锥度踏面的曲线通过性能总体趋势略优于大锥度踏面。3种踏面(LM、 LMG、LM磨耗踏面)在空、重车状态下以不同速度通过不同半径曲线的轮轴横向力Hy(kN)、轮轨横向力Fy(kN)、脱轨系数L/V和轮重减载率dQ/Q都没有超出标准规定的限制值。 图10 3种车轮型面轮轴横向力的对比Fig.10 Comparison of lateral axle forces for three wheelprofiles 图11 3种车轮踏面轮重减载率的对比Fig.11 Comparison of wheel unloading rate for three types of wheel profile 图12 3种车轮踏面脱轨系数L/V的对比Fig.12 Comparison of derailment coefficient for three types of wheel profile 磨耗预测时采用以下模型车轮磨耗模型采用基于硬度修正的Jendel磨耗模型[21],该模型是在Archard磨耗模型[22]的基础上,假定黏着区不发生磨耗,只在滑动区域发生磨耗。 结合Hertz+FASTSIM算法计算时,通过法向力计算获得椭圆接触斑,把接触斑划分为网格,网格长度分别为Δx和Δy,则可以将每一个网格内磨耗量表示为 (10) 式中:kw为磨耗系数;H为车轮表面硬度;Δd为相对滑动距离。接触单元上的法向力为 (11) 相对滑动距离表示为 (12) 式中:Δvx为纵向相对滑动速度;Δvy为横向相对滑动速度;vx为通过接触点的速度。 磨耗深度为 式中:pz(x,y)为接触网格上的法向力分布;a、b为接触斑长轴、短轴一半。磨耗系数是与接触斑单元上法向力和滑动速度相关的一个无量纲常数,磨耗系数直接决定着磨耗量的大小。 利用以上磨耗模型计算了车辆通过直线段的车轮磨耗,如图13所示,可以看出直线段速度为70 km/h,通过直线段时车轮型面优化前后的磨耗深度分别为8.1×10-9m和3.9×10-9m,减小51.8%,可以看出在直线段磨耗区域增大,主要接触区域在滚动圆附近。 图13 直线段车轮磨耗预测对比Fig.13 Comparison of wheel wear predictions for straight tracks 利用以上磨耗模型计算了车辆通过曲线段的车轮磨耗,如图14所示,曲线设置如下:直线段长100 m,缓和曲线90 m,圆曲线长200 m,超高100 mm。曲线外侧车轮磨耗如图14(a)所示,可以看出优化前后车轮磨耗深度分别为99.04×10-9m和44.71×10-9m,减小54.8%,曲线内侧车轮磨耗如图14(b)所示,优化前后车轮磨耗深度分别为58.58×10-9m和30.38×10-9m,减小48.13%,可以看出型面优化可以有效减小小轮径低地板驮背车直线段和曲线段和车轮磨耗,为抑制小轮径车轮磨耗,提升服役性能具有重要作用。 图14 曲线段车轮磨耗预测对比Fig.14 Comparison of wheel wear predictions for curved tracks 本文通过首先建立小轮径低地板驮背车转向架动力学模型,然后以减小轮轨接触应力为优化目标,利用轮径差反向设计法设计车轮型面,然后利用动力学模型和磨耗模型对优化前后型面的动力学性能和磨耗特性进行对比分析,主要得到以下结论: (1)本文采用轮径差反向设计法对小轮径低地板驮背车车轮型面进行优化,优化后型面进一步降低了车轮等效锥度,同时减小了轮轨法向接触应力。 (2)优化后车轮型面有效提升了小轮径低地板驮背车的车辆动力学性能,LMG踏面的临界速度最高,空车临界速度为196 km/h,较LM踏面提高23.3%,重车临界速度为209 km/h,较LM踏面增大17.54%;有效提升了车辆的横向平稳性指标和曲线通过性能。 (3)利用Jendel模型计算了直线段和曲线段车轮磨耗深度,优化后的车轮型面有效减小了小轮径转向架车轮磨耗可以在直线段减小51.8%,磨耗区域进一步增大。有效提升了小轮径转向架曲线通过性能,曲线外侧最大磨耗深度减小54.8%。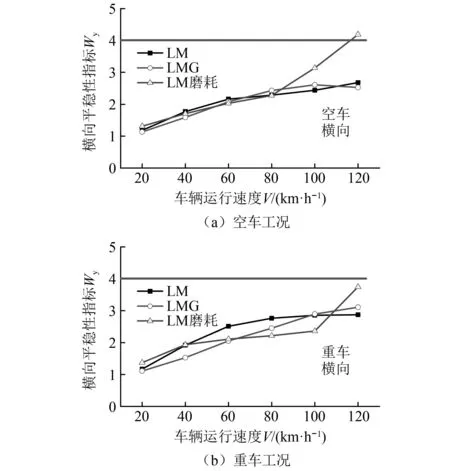
3.2 曲线通过性能
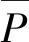
3.4 车轮磨耗性能
6 结 论
