基于声学黑洞波动控制技术的槽型轨动力吸振器减振降噪特性研究
2024-04-11师多佳赵才友张明凯
师多佳, 赵才友, 易 强, 张明凯, 高 鑫, 王 平
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,成都 610031;2.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100044)
有轨电车系统是公共交通的重要组成部分,被国际铁路联盟和各类能源与环境组织广泛推崇[1]。有轨电车轨道的建设成本低、周期短,同时具备较强的运输能力。因此,它既可以作为大城市内部现有轨道交通网络的补充线路,也可用于扩展地铁轨道交通网络至郊区,此外,它还能充当中小城市和大城市郊区的公共交通骨干线。有轨电车系统有效地填补了常规公交和轨道交通之间的空白,因此在一定程度上代表了现代城市轨道交通的发展趋势。然而,由于有轨电车系统运营在城市内部,对其振动和噪声产生的要求相对较高。根据以往的研究,在城市轨道交通系统噪声中,轮轨噪声占主导地位[2]。而从声源贡献角度来看,轨道是轮轨噪声中最重要的辐射源[3-4]。具体的减振降噪措施包括钢轨截面优化[5]、重型化和无缝化[6]、打磨维修[7]、施加约束阻尼材料[8]以及安装动力吸振器[9-10]等。这些措施旨在减少钢轨振动和噪声的产生,从而改善轨道交通系统的减振降噪效果。而相对于传统的轨道交通线路通常为左右对称结构的短平轨,现代有轨电车往往采用左右非对称结构的槽型轨,因此钢轨动力吸振器结构简单、安装维护方便、可进行形状设计的优势可以得到充分的发挥。尽管现有的钢轨动力吸振器在宽频内具有良好的减振降噪效果,但对于有轨电车更为严苛的噪声限值要求,仍然有望做进一步的提升。
声学黑洞(acoustic black hole, ABH)是一种新型振动控制技术,近年来在研究人员和工程师中引起了广泛的关注[11]。该技术的主要实现方法是通过调整结构组件的厚度,改变结构的阻抗,进而对结构的相位、群速度等特性产生影响。通过这种方式,能够将振动能量集中在特定的区域,并且只需要很少的阻尼材料就能够有效地将能量消耗掉,从而达到减振降噪的效果[12]。声学黑洞能够通过调控弹性波的传输,从而对局域能量的转移与损耗产生影响。相对于常规的主、被动控制方式,控制效率更高、频率范围更广[13-15]。目前声学黑洞波动控制技术已经在船舰、机械、航空航天等领域得到了广泛的应用,如金星等[16]针对船体板结构的振动控制,提出了一种带隙频段为78~115 Hz的新型幂指数棱台局域共振型声子晶体构型;赵楠等[17]在研究中提出了一种声学黑洞结构的分布式浮筏隔振系统,旨在进一步提高浮筏系统的隔振效果,从而达到更好地抑制舱室的机械噪声的目的。而万志威等[18]则将压电式分流阻尼的概念引入到声学黑洞梁式结构中,用半解析方法研究了该结构的振动特征,为声学黑洞结构在低频减振中的应用开辟了一条新途径。Zhou等[19-21]首次提出将ABH结构作为动力吸振器部件用于能量耗散和宽频振动控制,并将其连接到寄主结构的想法,以上这些研究拓展了声学黑洞技术的应用领域,并为改进振动控制效果提供了有益的方法和思路。在ABH结构声振耦合特性的数值研究方面,Deng等[22-24]提出了一种利用波和Rayleigh-Ritz的方法来计算复杂的频散曲线,并分析了ABH结构的带隙范围,发现ABH实现了显著的波衰减。然而,由于轨道系统与轮轨噪声的多样性、复杂性,声学黑洞波动控制技术运用到城市轨道交通减振降噪领域的研究并不多见。除此之外,声学黑洞效应主要通过减小主体结构的厚度来实现。然而,这样做会显著降低结构的强度和刚度。此外,受尺度、工艺等因素的影响,声学黑洞的有效起始频率往往很高,这给低频振动控制带来了很大的挑战。虽然动力吸振器能有效地抑制低频振动,但由于其控制频段窄、鲁棒性低,并且需要复杂的参数调整,限制了动力吸振器的应用范围和性能。因此,实现低频振动的有效控制仍然是一个具有挑战性的任务,需要进一步的研究和创新来解决这些问题。
本研究针对槽型轨振动噪声控制问题,将声学黑洞波动控制技术与动力吸振原理相结合,提出了一种新型的槽型轨动力吸振器。动力吸振器的振子采用橡胶材质,并且在上、下面分别贴上了等厚度的阻尼层,以实现高阻尼水平的同时尽量减小附加质量。研究成果将对有轨电车轮轨系统的振动和噪声控制具有一定的指导意义,并为未来类似工程的设计与优化提供指导。
1 声学黑洞型动力吸振器结构设计
1.1 声学黑洞型动力吸振器原理
动力吸振器(dynamic vibration absorber,DVA)的工作原理是在主体结构上附加有共振特征的次级结构。利用阻尼层的弹性-阻尼调谐效应,主结构的振动将传递到附加质量上。当附加质量的谐振频率与主结构的激励频率相匹配时,附加质量会吸收主结构振动的能量,从而有效减少主结构的振动响应。弹簧和阻尼层的参数也需要适当选择,以确保在特定频率范围内实现较好的振动控制效果。动力吸振器是由黏弹性元件和附加质量组成的附加系统。钢轨动力吸振器利用质量块的振动和阻尼材料的吸振特性来减少钢轨的振动。当钢轨受到外部激励时,动力吸振器通过谐振效应与钢轨一起共振,从而吸收和消耗钢轨的振动能量。阻尼材料在动力吸振器中起到重要的作用,通过吸收和分散振动能量,降低钢轨的振动响应。这样,钢轨动力吸振器实现了减振降噪的功能,有效地改善了钢轨系统的振动和噪声水平。
如图1所示,针对槽型轨设计了一种基于声学黑洞阻尼振子的动力吸振器。具体做法是将设计好的钢轨动力吸振器中的质量块挖出部分空腔,在每跨动力吸振器的中间位置建立连接构件,连接构件两端建立声学黑洞阻尼振子。新型声学黑洞阻尼(acoustic black hole damping, ABHD)结构通过连接构件与外部动力吸振器的钢振子进行刚性连接。该结构通过安装于连接构件两端的ABHD,通过声学黑洞效应和动力吸振原理,对外部动力吸振钢振子的弯曲波能量进行吸收与耗散,从而达到轨道系统减振的效果。该动力吸振器兼具了声学黑洞的宽带吸能特性和动力吸振器的单频减振能力,不但能在较宽的频带上实现减振,还可对特定的频率范围进行控制与调节。通过将这两种机制结合起来,该新型动力吸振器能够更有效地减小槽型轨的振动水平。

图1 声学黑洞型动力吸振器结构简图Fig.1 Structural diagram of ABHD-DVA
1.2 声学黑洞阻尼振子结构设计
图2展示了ABHD的结构简图,它由两个部分组成,一个是ABH结构,另外一个是阻尼层。在ABH结构的上、下面分别贴上了一层阻尼材料,起到了吸能和补偿ABH效应的作用。声学黑洞结构包括变宽度区域和宽度保持区域,其中变宽度区域的长度为x1-x0,宽度变化函数为幂函数;由于实际加工的限制,边缘宽度无法逐渐减小到零,因此在逐渐变窄的截面边缘处有一个截断宽x0,同时为保持这个截断宽度的连续性,应当延伸出一个宽度为h0/2的均匀的平台。从一维声学黑洞的对称性出发,可以得到ABH的半截面厚度与位置的对应关系式。
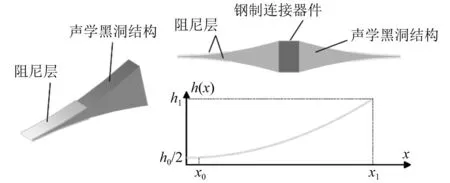
图2 ABHD振子结构简图Fig.2 Structure diagram of ABHD vibrator
(1)
式中:h(x)为截面厚度;h0为截断厚度;x为位置坐标;x0为平台长度;a为常数系数;x1为声学黑洞结构长度;m为指数。
2 振动噪声预测模型
2.1 附加ABHD-DVA的槽型轨有限元模型
COMSOL Multiphysics多物理场仿真软件为研究ABHD-DVA的振动特性和降噪效果提供了强大的多物理场建模和仿真模块。动力吸振器主体采用钢材,ABH结构采用PA6(polyamide 6)橡胶,阻尼层为VHB(very high bond)阻尼材料,各部件的材料物理参数如表1所示。为兼顾模型计算的准确性与计算效率,本文建立了20跨槽型轨标准轨道,为了降低计算结果受弹性波反射影响的程度,在钢轨的两端采用了低反射边界条件。这些边界条件的设置旨在减少弹性波在边界处的反射,以提高计算结果的准确性。将设计的ABHD-DVA固定在钢轨的两侧,如图3所示。钢轨用59R2型槽型轨,ABHD-DVA结构由钢轨橡胶层、盒式连接器件(钢振子外壳和连接构件)和ABHD振子组成。其中,所述钢振子外壳的总体尺寸为300 mm×20 mm×35 mm,并且具有2 mm的厚度。中间连接构件的大小为20 mm×16 mm×31 mm。两个同样大小的ABHD振子分别安装在连接构件的两边,其几何参数如表2所示。阻尼层尺寸为50 mm×15 mm×1 mm。在槽型轨的下部设置离散面弹簧支座,扣件间距设为0.6 m,扣件垂向刚度为4×107N/m,垂向阻尼为3.2×106N·s/m,扣件纵向长度为0.3 m。激励点作用于跨中位置的钢轨截面最高点处,激振力F为简谐单位力。

表1 材料物理参数
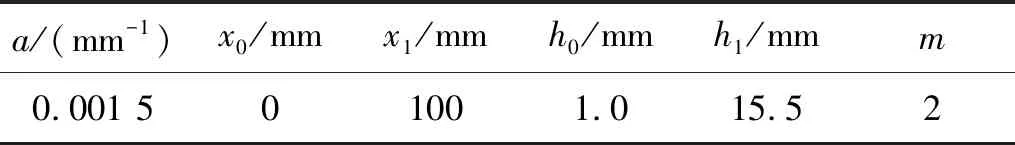
表2 声学黑洞结构几何参数
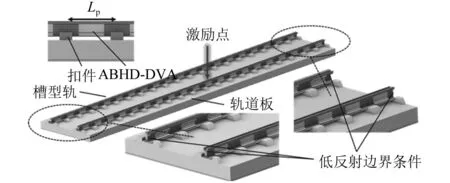
图3 附加声学黑洞型动力吸振器的槽形轨三维实体有限元模型Fig.3 3D solid finite element model of channel rail with acoustic black hole type dynamic vibration absorber
为了评估ABHD-DVA的振动特性以及降噪效果,本文建立了3种不同的动力吸振器模型:ABHD-DVA是指在钢制连接器件的两边附加声学黑洞阻尼振子,如图4(a)所示;等质量阻尼动力吸振器(equal mass damping-DVA,EMD-DVA)是指在钢制连接器件的两端附加等质量阻尼的悬臂梁振子,并经过结构设计获得与ABHD振子相同的质量、长度、阻尼和材料特性,如图4(b)所示;传统动力吸振器(traditional dynamic vibration absorber, T-DVA)为了保持对比效果,连接构件不附加振子,如图4(c)所示。3种不同的槽型轨动力吸振器局部示意图如图4所示。
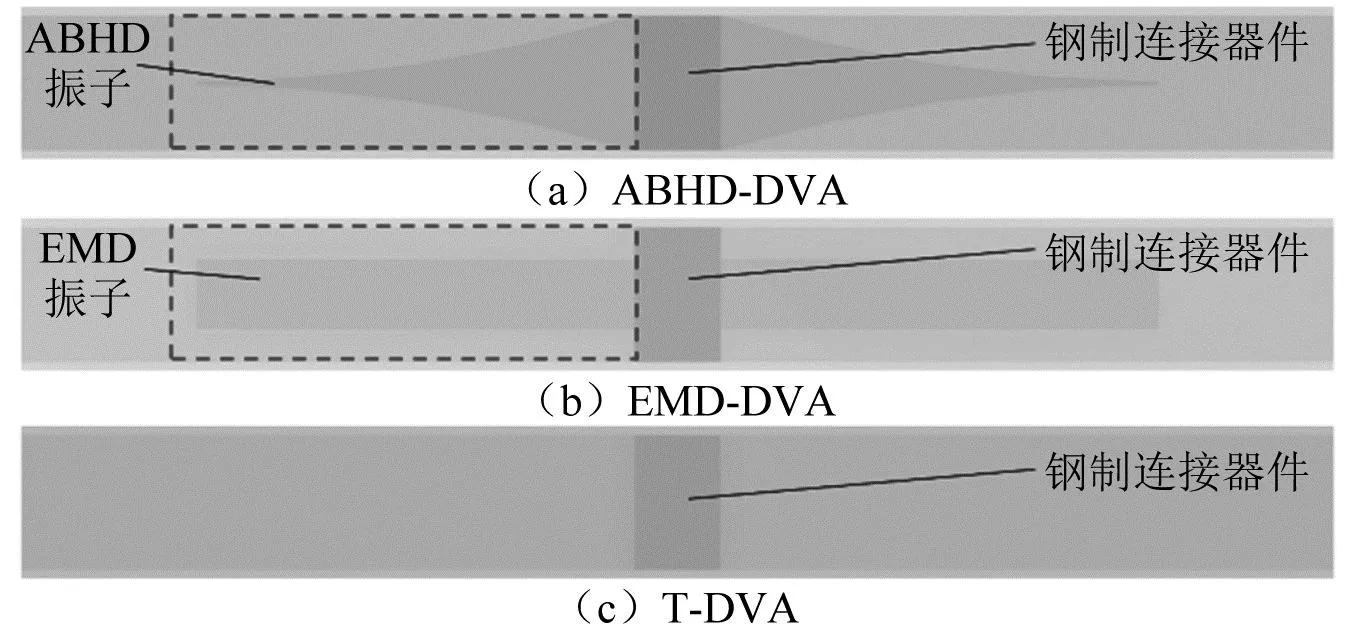
图4 3种不同动力吸振器的局部示意图Fig.4 Partial schematic of three different DAVs
2.2 导纳特性与表面振动加速度
为研究槽型轨的振动噪声特性,需要对其模态进行分析,求解出其共振频率。这是进一步进行减振降噪研究的基础。如图5所示,利用多物理场仿真软件COMSOL Multiphysics对59R2槽型轨进行模态分析。采用ARPACK特征频率求解器,对建立的单跨槽型轨的纵向端面施加周期性边界条件,同时对槽型轨底部扣件作用位置施加离散面弹簧支座,在特征频域模块下进行参数化扫描。在通常车速下,钢轨辐射噪声的有效频率在3 000 Hz以下,故本文仅计算3 000 Hz以下频段的槽型轨模态。
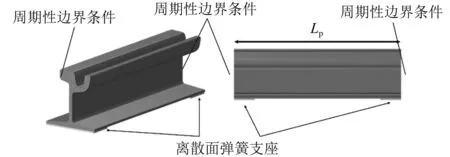
图5 槽型轨周期子结构的波导模型Fig.5 Waveguide model of channel rail periodic substructure
频率响应表征了系统受单位力作用时的动态响应,能较好地反应系统的振动特征。故分别计算附加3种不同动力吸振器的槽型轨的频响函数,并与不附加钢轨吸振器的槽型轨频响函数进行对比,以分析ABHD-DVA的减振效果。计算频率为0~3 000 Hz,步长为10 Hz。频域分析得到槽型轨的垂向振动位移幅值及速度幅值,通过谐响应分析再得到槽型轨垂向振动位移导纳及速度导纳。在此基础上,将垂向速度导纳乘以轮轨相互作用力,从而得到钢轨垂向振动速度,该振速可应用于轨道辐射噪声分析。
2.3 导纳特性与表面振动加速度
振动衰减率是描述钢轨垂向或横向弯曲波的振幅衰减随钢轨纵向位置变化的函数。它可以通过计算单位脉冲激励下各位置的振动频率响应函数来确定。通过测量1/3倍频程每个中心频率处的一系列测点上的频响函数,可以计算得到钢轨的振动衰减率[25]。
(2)
式中:A(x0)为激励处的速度导纳;A(xn)为测点n处的速度导纳;Δxn为测点n距离激励处的距离。
2.4 槽型轨声辐射特性
钢轨受到单位荷载作用时发生振动,进而沿着钢轨纵向传播并辐射噪声。通过基于槽型轨振动计算模型得到槽型轨垂向振动位移/速度响应,可以进行声辐射特性的计算分析。
2.4.1 槽型轨声辐射效率
声辐射效率,也被称为辐射系数或辐射比,是结构振动与声辐射之间的关键参数。它表示结构向半空间辐射的声功率与置于无限大障板上的活塞辐射的声功率之比。声辐射效率的物理意义在于衡量结构振动转化为声辐射的效率,即结构振动能量向声波能量的转换程度。通过计算声辐射效率,可以评估结构的声辐射特性并优化结构设计以降低噪声辐射[26]。
本节联合有限元法和边界元法计算槽型轨声功率辐射效率。有限元模型计算得到响应后,利用声学软件LMS Virtual.Lab建立钢轨的边界元模型。边界元法与有限元法在思想上有所不同。有限元方法是对连续区域进行单元划分,而边界元方法只在定义区域的边界上进行单元划分,如图6(a)、图6 (b)所示。在钢轨的边界元模型中,只在钢轨的表面边界上进行单元划分。边界元网格划分对分析精度具有重要影响,声学边界元模型的单元尺寸应服从“最小分析波长至少要有6个单元”的基本原则,即计算频率最短波长的1/6要大于最大单元的边长[27]。通过将轨道结构的三维有限元模型计算得到的钢轨振动响应作为边界条件应用于钢轨的声学边界元模型中,可以计算出槽型轨表面的辐射声功率,并同时计算出槽型轨振动的声辐射效率,如图6(c)所示。从图6(c)中可以看出,在低频范围(1 000 Hz以下),槽型轨的声辐射效率与频率基本成正比关系,在1 000 Hz以上的较高频范围内,钢轨的声辐射效率接近于1,而附加ABHD-DVA后槽型轨的声辐射效率在重点关注的500~1 500 Hz的控制频段得到了很大程度的降低,这是因为ABH内弯曲波速度较慢,降低了声辐射效率,从而无法向远处贡献声能量。

图6 槽型轨边界元模型和ABHD-DVA槽型轨边界元模型及声辐射效率Fig.6 Acoustic boundary element model of channel rail and acoustic boundary element model of channel rail with ABHD DVA and sound radiation efficiency
2.4.2 槽型轨声功率级
轨道声功率是指钢轨声能的变化程度,其与轨道的振动衰减率等诸多因素相关,而与受声点的位置无关。在本节中,采用理论分析方法与2.4.1小节的边界元仿真模拟相结合,分析钢轨振动衰减率与原点速度导纳,从而获得单位简谐荷载作用下的声功率级。这一计算结果可以用来评估钢轨在不同频率下的声辐射水平。
无限长钢轨的声功率W可表示为
(3)
式中:v(x)为钢轨在x位置处的振动速度幅值;ρ0c0为空气声特性阻抗,ρ0=1.225 kg/m3为空气密度,c0=340 m/s为声音在空气介质中的传播速度;σ为槽型轨声辐射效率;P为一个截面的周长,对于槽型轨的垂向振动,该值为钢轨截面轮廓线在水平方向上的投影总长度[28],即0.558 m。
假设钢轨的垂向振动沿着线路纵向呈现指数的衰减传播
|v(x)|=v(0)e-β|x|
(4)
式中:v(0)为基准点上的振动速度幅值;β为轨道频响函数振幅的衰减系数。由于线路纵向的对称性
(5)
将衰减系数转换成dB/m为单位的衰减率形式,Δ=8.686βdB/m,则
(6)
基准声功率W0=1×10-12W,将声功率转换为声功率级
(7)
式(7)说明了随着衰减率和导纳幅值越高,其声功率级逐渐降低。通过计算得到的各频率下声功率级后,可以根据式(8)进行叠加,从而得到钢轨的总声功率级
(8)
3 数值仿真与分析
3.1 槽型轨模态分析
研究槽型轨的模态特性对于分析轨道系统的振动和噪声具有重要意义。通过分析槽型轨的固有频率和振型,可以了解系统的振动行为、寻找共振频率,并设计相应的减振措施来降低振动和噪声水平。
由于槽型轨不同于其他型号的钢轨,其轨头两侧呈现不对称的特点,它的各向模态尤为复杂。在237.8 Hz、256.0 Hz、295.9 Hz、449.3 Hz、1 489.1 Hz、1 874.9 Hz等频率下均会产生垂向共振,槽型轨模态会发生拱起,截面并无明显变形。一阶pinned-pinned共振频率为983.3 Hz。在这种情况下,当槽型轨受到激励时,纵向机械波在轨枕之间形成驻波,节点正好位于扣件支承处,波峰处于跨中位置的1/2处,振型图如图7(a)所示。二阶pinned-pinned共振频率为2 360.9 Hz。在这种情况下,跨中以及扣件节点处均为驻波节点,波峰分别位于跨中的1/4处和3/4处。振型图如图7(b)所示。
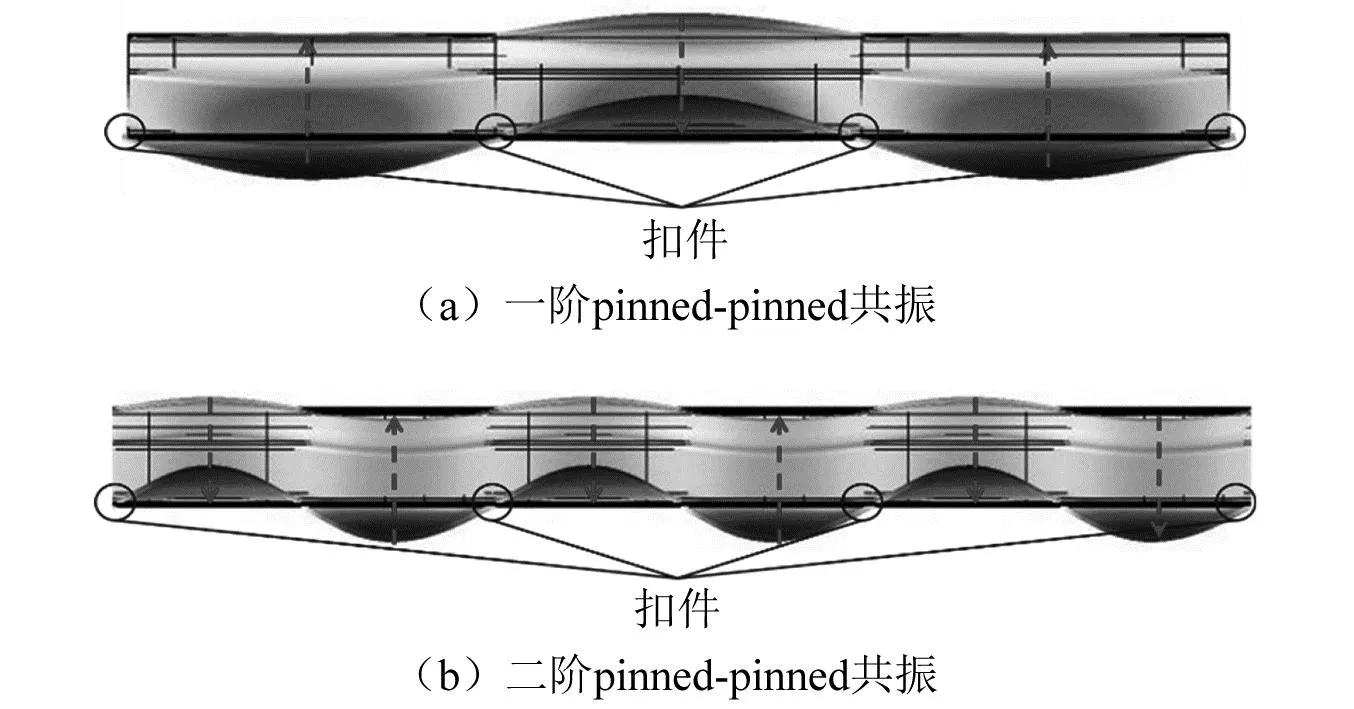
图7 槽型轨垂向弯曲模态Fig.7 Vertical bending modes of channel rail
3.2 不同动力吸振器减振降噪性能对比
本节探讨不同动力吸振器的减振降噪性能,减振效果通过原点位移导纳和振动衰减率描述,降噪效果通过槽型轨垂向振动声功率级和总声功率级描述。
3.2.1 减振效果
图8(a)为不同动力吸振器与标准槽型轨的原点位移导纳。可以看出,在400 Hz与1 500 Hz附近存在着明显的峰值,与Ⅰ、Ⅲ处的垂向共振频率对应。同时,在983.28 Hz与2 360.9 Hz附近存在着的共振峰则与Ⅱ、Ⅳ处的槽型轨前两阶pinned-pinned共振峰频率对应。同样在槽型轨跨中节点施加单位简谐荷载,对比分析标准槽型轨、T-DVA、EMD-DVA和ABHD-DVA的位移导纳区别。由于附加质量弹簧阻尼系统的存在,轨道结构整体质量增加,这会导致原点位移导纳的共振峰向低频移动,并呈现不同程度的下降。这意味着在频率响应中,原本位于高频段的共振峰向低频偏移,振幅减小。在120~670 Hz、890~1 160 Hz频段内槽型轨的振动位移导纳减小,槽型轨在这一频率范围内的振动能得到很好的抑制。Ⅰ、Ⅱ处位移导纳的共振峰可以看出,传统动力吸振器通过提高质量来将共振峰向低频移动,以避免在原有频段上出现槽型轨的共振峰。然而,当槽型轨发生共振模态时,传统动力吸振器并不能有效地抑制钢轨的振动。观察可发现附加ABHD-DVA的槽型轨位移导纳相比于附加T-DVA的槽型轨位移导纳在Ⅰ、Ⅱ、Ⅲ处均有较大削减,特别是在Ⅰ和Ⅱ处;而附加EMD-DVA时,位移导纳在各个频段与T-DVA相比并无明显削减。这是EMD-DVA中的EMD振子仅具有有限的作用频率范围所致,与T-DVA的原理相似。而ABHD-DVA中的ABHD振子不仅具有动力吸振的作用,还具备ABH宽频能量吸收器的功能,可以实现更广泛的频带减振效果。图8(b)表明了标准槽型轨和附加3种不同动力吸振器的槽型轨对振动衰减率的影响频段集中在800 Hz以上,在800~1 000 Hz内,一阶pinned-pinned振动响应较大。在这个频段内,无动力吸振器的标准槽型轨的振动衰减率为0.68 dB/m。然而,安装ABHD-DVA后,振动衰减率增加到1.80 dB/m,提高率达265%
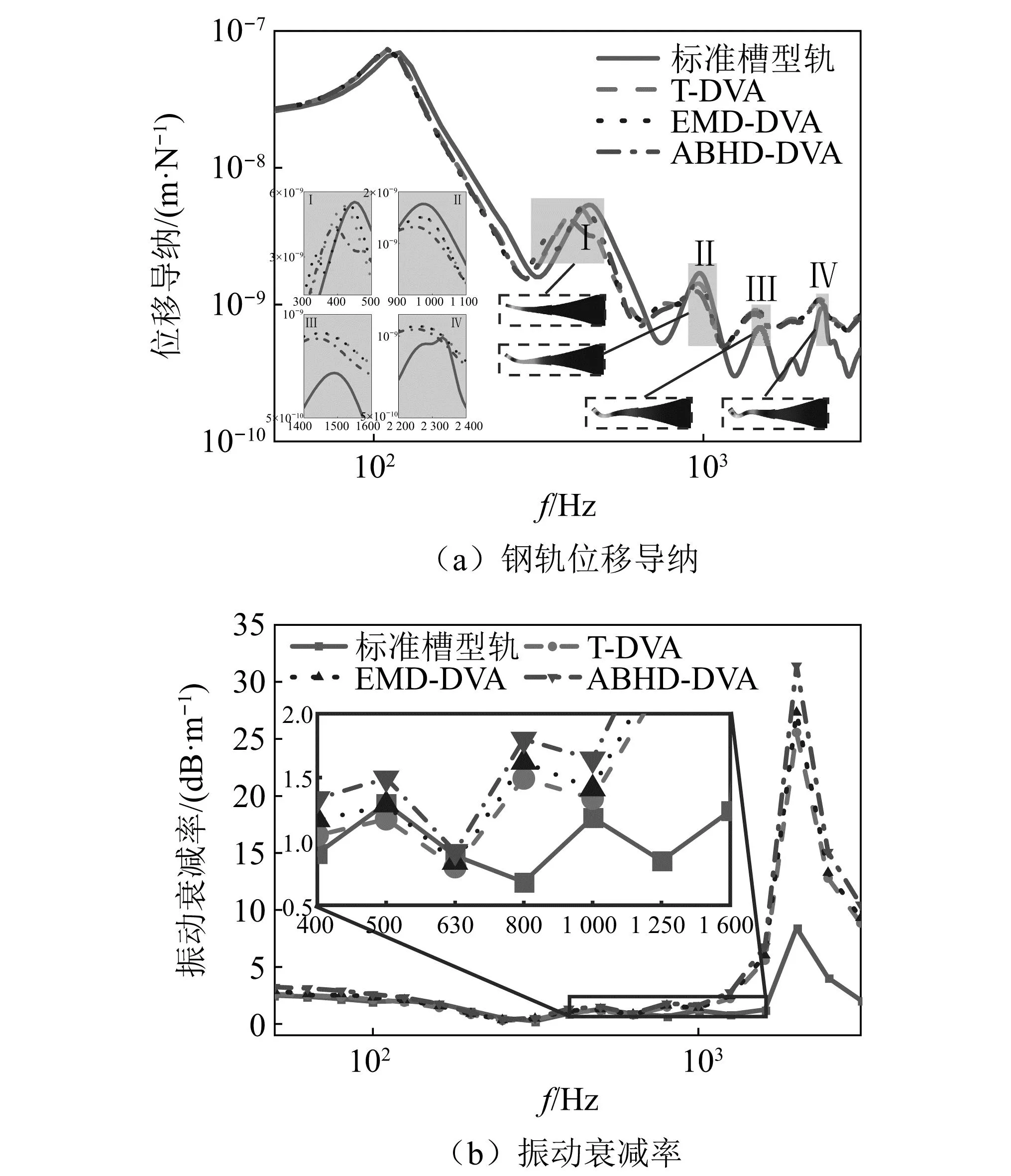
图8 槽型轨和3种动力吸振器对位移导纳和振动衰减率的影响Fig.8 The influence of channel rail and three DVAs on displacement admittance and vibration attenuation rate
3.2.2 降噪效果
图9(a)描述了槽型轨的声辐射特性,槽型轨在500~3 000 Hz的频段内声功率级较高,这也是轮轨噪声重点关注的频段。由图10可知在1 000 Hz频段附近,ABHD-DVA相较于EMD-DVA和T-DVA的降噪效果更为突出,将钢轨噪声从44.28 dB降低到38.04 dB,降低了6.24 dB。由图9(b)可知:ABHD-DVA将总声功率级降低了4.9 dB;相较于T-DVA总声功率降低了0.96 dB;相较于EMD-DVA降低了0.64 dB。
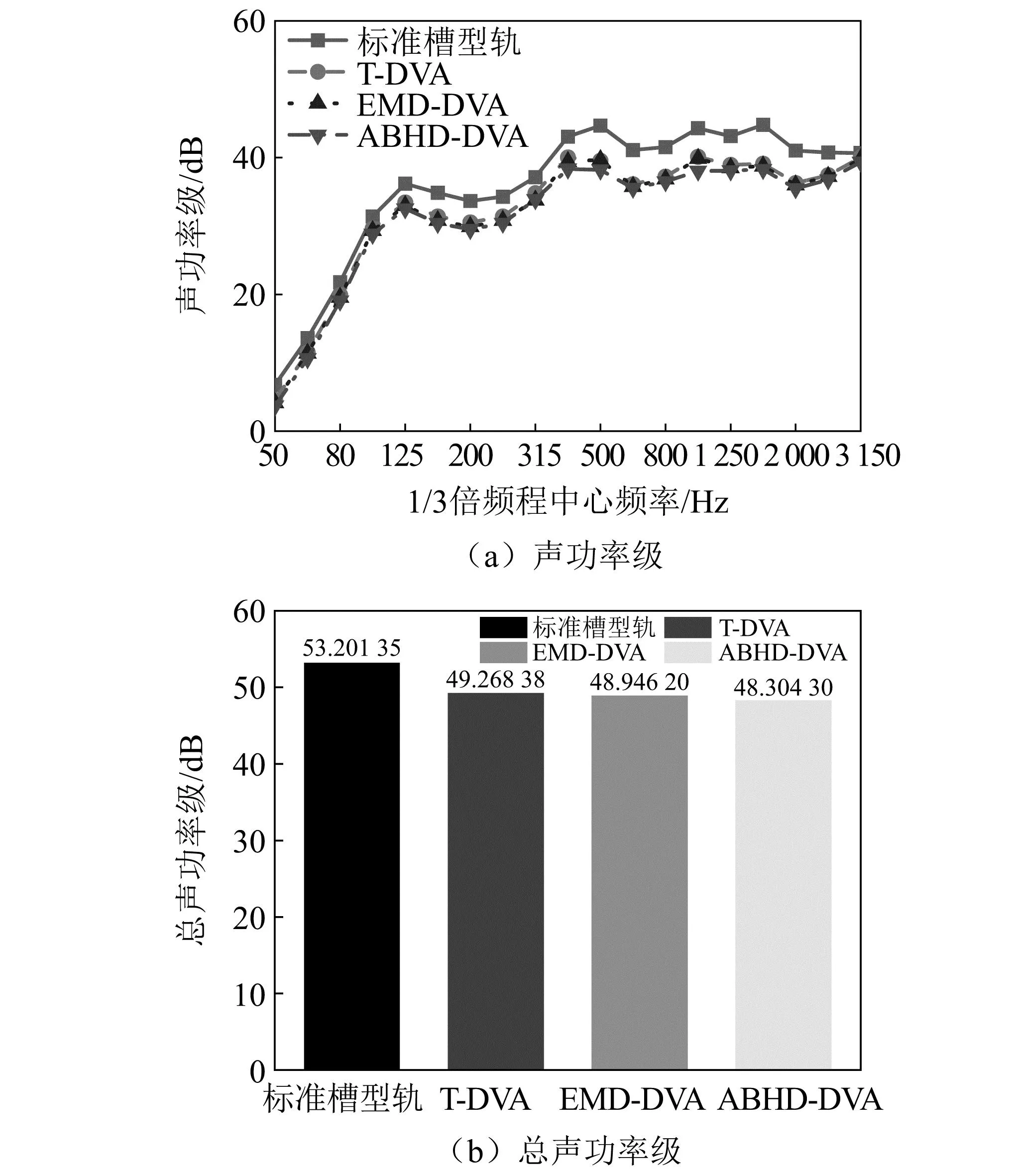
图9 槽型轨和3种动力吸振器对声辐射功率的影响Fig.9 The influence of channel rail and three DVAs on the radiated sound power
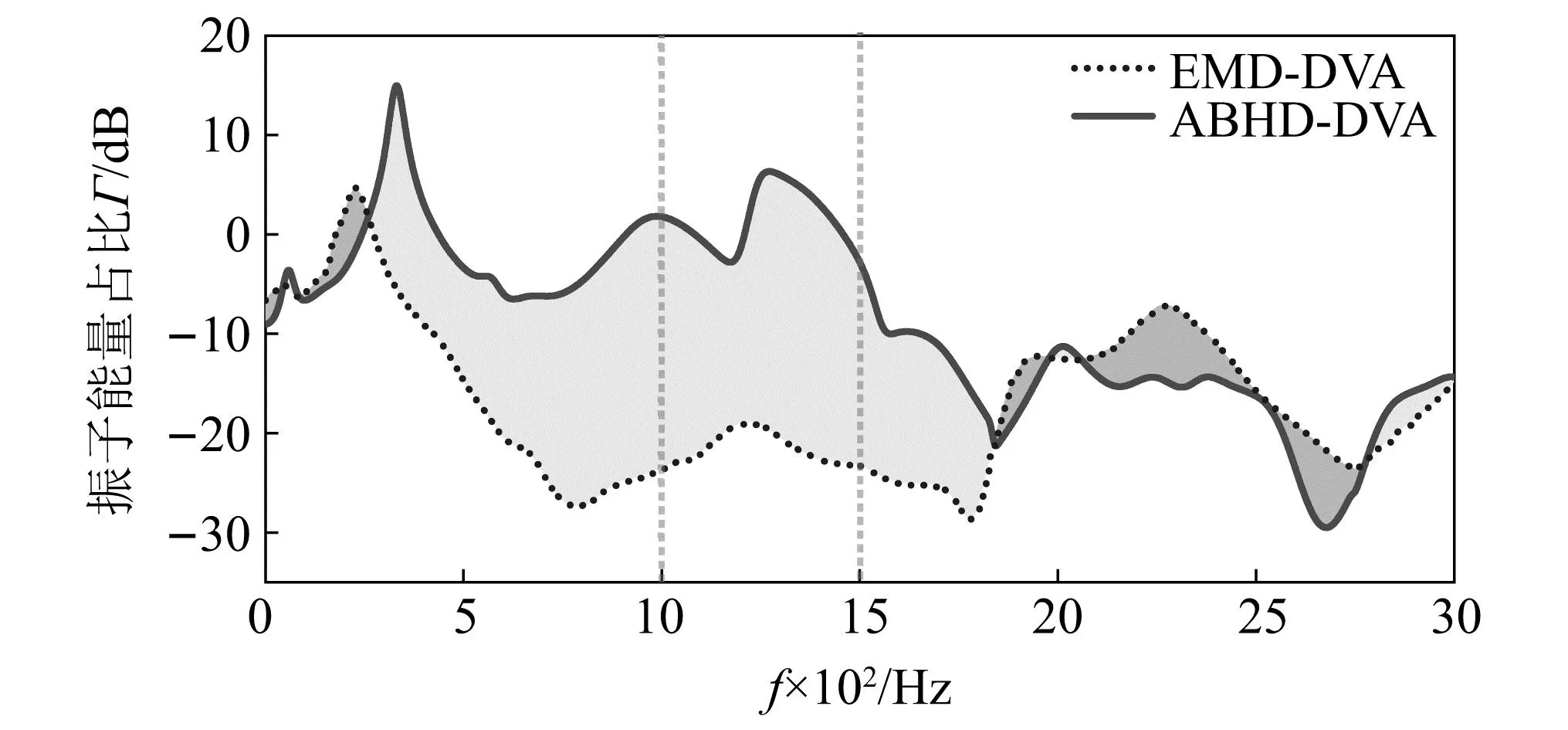
图10 不同动力吸振器的振子能量与整个系统能量占比Fig.10 Proportions of vibrator to whole-system energy in different DVAs
3.2.3 原理分析
在3.2.1节及3.2.2节的基础上,通过对ABHD-DVA和EMD-DVA振子能量占比水平的比较,深入挖掘两种结构的减振降噪机理。为表示转移到振子上的振动能量的程度,定义ABHD振子和EMD振子上的振动能量占整个系统振动能量的比值为η
η=10lg(Evibrator/Esystem
(9)
式中:Evibrator为振子的动能与弹性应变能之和;Esystem为系统的动能与弹性应变能之和。比较ABHD-DVA和EMD-DVA的振子能量占比时,假设它们具有相同的约束条件和荷载激励方式,且阻尼层的能量损耗因子均设为0.1。从图10中可以清楚地看到,与传递给EMD振子的振动能量相比,系统转移到ABHD振子更为显著。尽管由于两种振子的共振频率差异,在某些频率处振动能量占比曲线的峰值出现偏移,然而在重点关注的500~1 500 Hz共振峰激增频段,ABHD-DVA振子振动能量占比明显高于EMD-DVA。造成这一现象的根本原因在于振子和动力吸振器之间的相互作用,在系统自振频率接近的情况下,振动能量会向连接器两边的振子处聚集,从而产生峰值。
与EMD振子相比,ABHD振子同时具有动态振动吸收和宽频带能量吸收的功能,即ABH效应。然而,这种效应通常发生在中频段和高频段,见图6(a)。ABHD振子的变形主要集中在振子顶端区域,这使得更多的弯曲波能量集中在振子顶端,导致系统能量损失系数的显著增加。此外,ABHD振子具有更灵活的动态特性,增强了ABHD振子与动力吸振器之间的频率匹配能力与振动吸收性能,并在更宽的频率范围内高效的将振动能量从DVA系统转移到ABHD振动器上。
3.3 ABHD-DVA参数影响分析
3.3.1 阻尼层厚度的影响
在ABHD-DVA振子阻尼层损失因子为η=0.1时,计算阻尼层厚度分别为0、1 mm、5 mm,如图11所示。由图11(a)可知,没有阻尼层的ABHD-DVA会增加槽型轨的共振频率和响应峰值,对减振降噪不利。阻尼层厚度为1 mm时的位移导纳峰值小于阻尼层为5mm时的峰值,说明当阻尼层厚度过大时,ABHD振子无法有效发挥减振作用;图11(b)中,在800~1 000 Hz频段附近,阻尼层厚度为1 mm时振动衰减率明显大于阻尼层厚度为0和5 mm时,同样说明阻尼层厚度不宜过大。由图11(c)可知,当ABHD振子阻尼厚度适中(1 mm)时,降噪效果好于不施加阻尼层,且与阻尼层厚度较大(5 mm)时的降噪效果相当,图11(d)同样证明这一点,采用合适的阻尼层厚度可以降低钢轨总声功率级达1.34 dB。
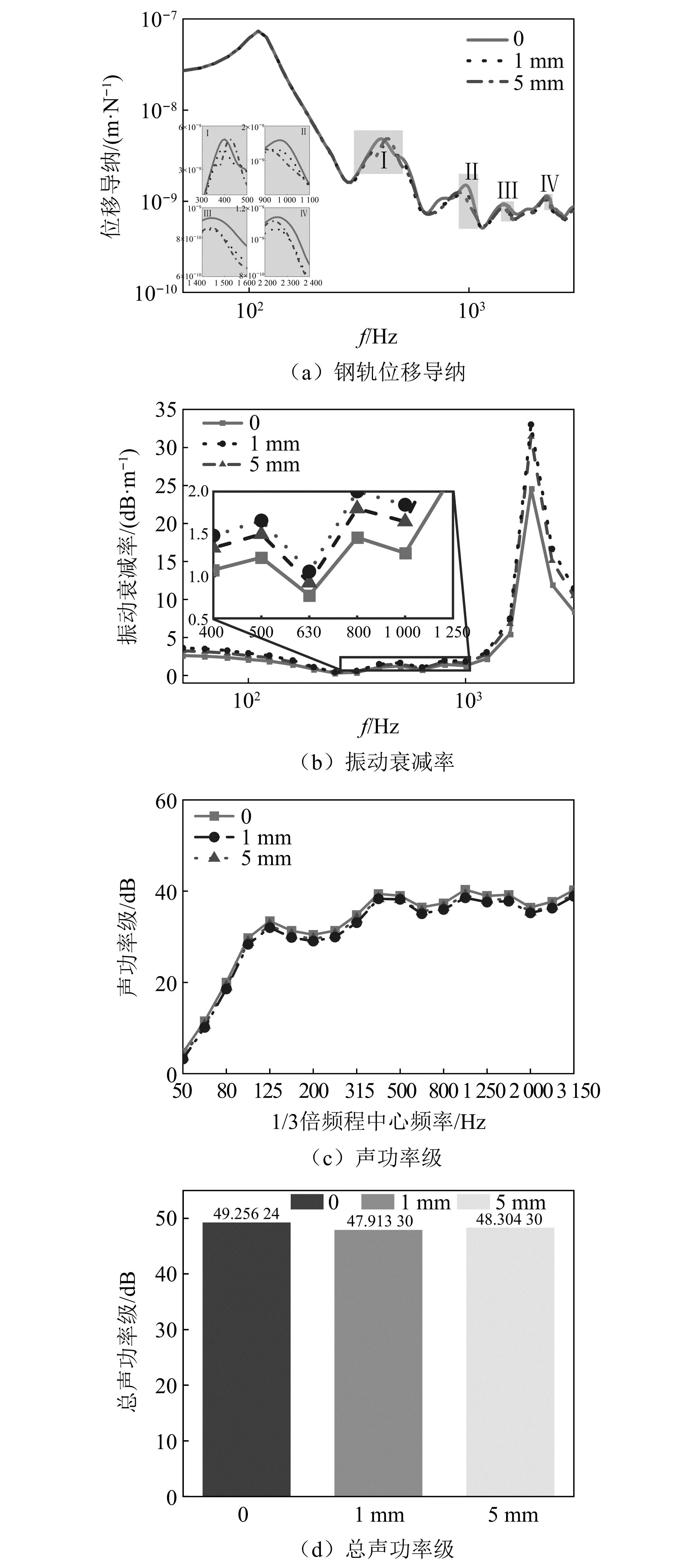
图11 阻尼层厚度的影响Fig.11 Influence of damping layer thickness
3.3.2 阻尼层损失因子的影响
在ABHD-DVA振子阻尼层厚度为1 mm时,计算阻尼层损失因子分别为0.005、0.1、0.5,如图12所示。由图12(a)和图12(b)可知,阻尼层损失因子越高,钢轨位移导纳越小,振动衰减率越高,由此可见,ABHD振子阻尼层损失因子越大,为了扩大ABHD-DVA的调谐频段,需要增加阻尼系数,但在仿真计算中应考虑阻尼层材料的实际限制。由图12(c)和图12(d)可知,阻尼层损失因子的增大会对钢轨噪声起到部分抑制作用,当阻尼损失因子从0.005增至0.1时,钢轨总声功率级降低了0.95 dB,但当阻尼损失因子从0.1增至0.5时,钢轨总声功率级仅降低了0.50 dB,由此可知过度的增大阻尼层损耗因子虽可以降低钢轨总声功率级,但其降低幅度过小,得不偿失,故在后续结构设计中将阻尼层损失因子取得适中值0.1。
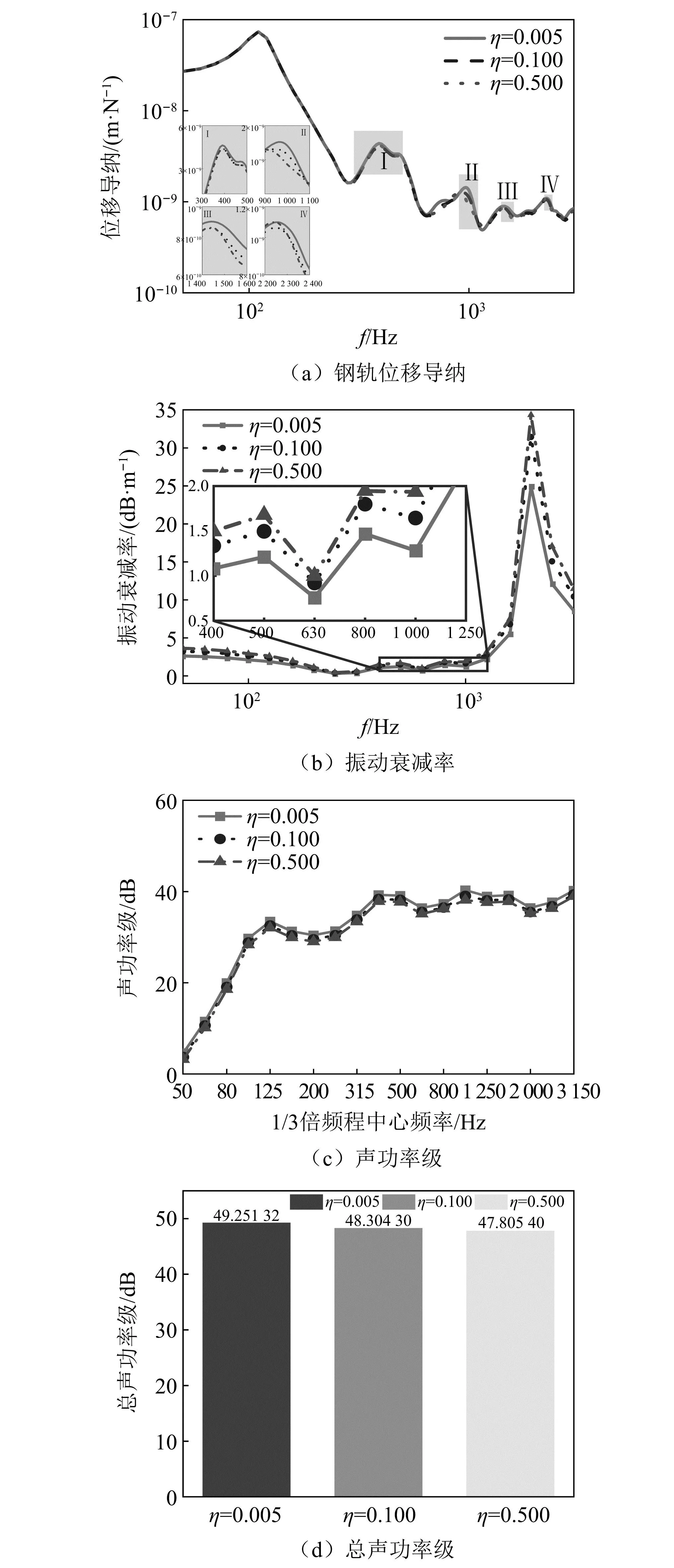
图12 阻尼层损耗因子的影响Fig.12 Effect of damping layer loss factor
4 结 论
在本研究中提出了一种新型的槽型轨道动力吸振器,将声学黑洞波动控制技术与动力吸振原理相结合。该吸振器设计的目标是保证主结构强度与刚度的前提下,采用附加的声学黑洞阻尼振子作为吸能单元,对主结构的振动能量进行传递、吸收与耗散。此外,为了研究声学黑洞型动力吸振器对槽型轨道振动特性和声辐射特性的影响,利用仿真分析对不同类型的动力吸振器下槽型轨道的导纳和振动衰减率特性进行了评估。最后,使用滚动噪声预测模型对ABHD-DVA的降噪效果进行了计算和分析,并研究了ABHD-DVA参数对轮轨振动和噪声的影响规律。主要结论如下:
(1)利用仿真分析对不同类型的动力吸振器下槽型轨道的位移导纳和振动衰减率进行了评估,验证了ABHD-DVA在能量聚集和耗散方面的高效性,这为动力吸振器在振动和噪声控制方面开辟了一条新途径。
(2)在800~1 000 Hz内,一阶pinned-pinned振动响应较大。在这个频段内,无动力吸振器的标准槽型轨的振动衰减率为0.68 dB/m。然而,安装ABHD-DVA后,振动衰减率增加到1.80 dB/m,提高率达265%。ABHD-DVA相较于EMD-DVA和T-DVA的降噪效果更为突出,将钢轨噪声从44.28 dB降低到38.04 dB,降低了6.24 dB。
(3)没有阻尼层的ABHD-DVA会增加槽型轨的共振频率和响应峰值,对减振降噪不利。阻尼层厚度为1 mm时的位移导纳峰值小于阻尼层为5 mm时的峰值,说明当阻尼层厚度过大时,ABHD振子无法有效发挥减振作用。当阻尼层厚度为1 mm时可以降低钢轨总声功率级达1.34 dB。
(4)ABHD振子阻尼层损失因子的增大会对钢轨噪声起到部分抑制作用,当阻尼损失因子从0.005增至0.1时,钢轨总声功率级降低了0.95 dB,但当阻尼损失因子从0.1增至0.5时,钢轨总声功率级仅降低了0.50 dB,由此可知过度的增大阻尼层损耗因子虽可以降低钢轨总声功率级,但其降低幅度过小,在结构设计中将阻尼层损失因子设为0.1最为合适。
