不确定性简谐激励下连续体结构可靠性拓扑优化
2024-04-11时元昆
王 选, 时元昆, 陈 翔, 龙 凯
(1. 合肥工业大学 土木与水利工程学院,合肥 230009; 2. 天津大学 机械工程学院,天津 300072;3. 华北电力大学 新能源电力系统国家重点实验室,北京 102206)
在航空航天、汽车、船舶等领域中,结构系统或机器中的振动和噪声主要来源于旋转部件引起的谐波力。为了保证结构系统或机械装置的使用安全性和舒适性,通常对结构的动力学性能要求很高。一方面,要求结构的低阶固有频率远离外激励频率,防止发生共振现象,造成结构破坏[1-2];另一方面,要求结构尽可能降低振动强度,将振动对装置和人员的损害降到最低[3-4]。因此,为了改善结构的动力学性能,开展结构动力学拓扑优化研究具有重要意义。早期关于动力学拓扑优化问题的研究主要以结构的固有频率为约束或目标,或者优化给定阶数的两个相邻高阶特征频率之间的间距等[5-6]。而考虑简谐激励下的动响应分析可帮助设计人员预测结构的持续性动力特性。简谐激励下的结构优化设计对于抑制其振动响应具有重要意义。
近年来,简谐激励下结构动响应拓扑优化受到越来越多的关注。Ma等[7]基于均匀化方法研究了简谐激励下无阻尼结构的动柔度最小化问题。龙凯等[8]基于独立连续映射方法建立了以结构体积最小化为目标,以关注自由度振幅平方和为约束的确定性优化模型,并研究了激励频率、阻尼系数和激励振幅对优化结果的影响。Liu等[9]针对谐响应下大规模拓扑优化问题,讨论了模态位移法、模态加速度法和全分析方法的计算效率。房占鹏等[10]基于渐进结构优化法实现了指定频带简谐激励下的约束阻尼结构布局优化设计。Niu等[11]针对简谐激励下振动响应最小化问题,总结和比较了一些常用的目标函数,包括动柔度、局部结构位移响应、结构加速度等。Zhao等[12]将模态叠加法与模型降阶法相结合,研究了谐波激励下具有比例阻尼的大尺度结构的拓扑优化问题。徐家琪等[13]基于自然单元法研究了谐波激励下结构动柔度最小化问题。Long等[14]基于二次规划算法实现了简谐激励下应力约束拓扑优化问题的求解。Montero等[15]提出了一种基于密度加权范数的目标函数解决连续体结构在谐波激励下的拓扑优化问题。Zhao等[16]提出了一种自适应混合展开法并验证了其在谐波激励下求解拓扑优化问题的有效性。Wang等[17]采用拓扑优化方法实现了谐响应下结构的保形拓扑优化设计。Wang等[18]提出了一种结合二阶Krylov子空间和多重网格法的降阶方法,用以求解简谐激励下多相材料结构的拓扑优化设计问题。
不难看出,上述简谐激励下结构动响应拓扑优化的研究都是在确定性条件下开展的[19],忽略了简谐激励振幅和频率等不确定性因素对优化结果的影响,可能会导致结构动力学性能对不确定因素的影响过于敏感,结构的可靠性水平较低。目前考虑不确定性的结构拓扑优化可分为两类:鲁棒性拓扑优化[20]和可靠性拓扑优化(reliability-based topology optimization, RBTO)[21-22]。鲁棒性拓扑优化旨在增强结构抵抗不确定性因素干扰的能力。可靠性拓扑优化旨在设计满足指定可靠性水平的结构。目前已有一些学者尝试将考虑不确定性因素的鲁棒性设计理论整合到谐响应拓扑优化中,以提高动响应结构抵抗不确定性激励干扰的能力。Zhang等[23]研究了未知但有界的简谐激励下的结构鲁棒拓扑优化问题,其中优化目标是最小化最坏情况的动柔度。王栋[24]基于变密度方法研究了简谐激励作用位置不确定性情况下结构动态鲁棒性拓扑优化设计,以降低结构对载荷作用点随机扰动的影响。Valentini等[25]采用分层抽样的蒙特卡罗模拟方法对结构动力响应的期望值和标准差进行建模,研究了考虑激励频率不确定性的最小化结构动态响应的鲁棒性设计。
与上述鲁棒性拓扑优化工作不同,本文旨在将考虑不确定性的可靠性分析理论整合到谐响应拓扑优化问题中,针对不确定性简谐激励下连续体结构的可靠性设计问题,提出了一种考虑简谐载荷振幅大小和频率不确定性的可靠性拓扑优化方法,以设计满足指定可靠性水平的动响应结构,确保结构在不确定性简谐激励下的失效概率小于或者等于指定的失效概率。
1 简谐激励下确定性拓扑优化
1.1 谐响应有限元分析
简谐激励下结构的动力学有限元方程为
(1)
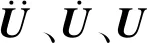
结构整体刚度矩阵和质量矩阵可分别通过组装对应的单元刚度矩阵和单元质量矩阵得到,其表达式为
(2)
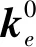
本文采用工程中常见的比例阻尼,故阻尼矩阵可表示为刚度矩阵和质量矩阵的线性组合
C=cmM+ckK
(3)
式中,cm和ck为比例阻尼系数。
令U=ueiωt并将其代入式(1)可得
(K-ω2M+iωC)u=F
(4)
进一步简化式(4)可得
Kdu=F
(5)
式中:Kd为阻尼系统的等效刚度矩阵,即动刚度矩阵,Kd=K-ω2M+iωC; 这里位移振幅u为一个复向量。
1.2 简谐激励下确定性拓扑优化模型
由于简谐激励下结构的振幅反映了结构的振动强度,为了抑制结构在简谐激励下的振动行为,以所关注自由度对应的振幅平方和为约束,以结构相对于初始状态的体积比为目标,建立简谐激励下确定性拓扑优化(deterministic topology optimization,DTO)模型为
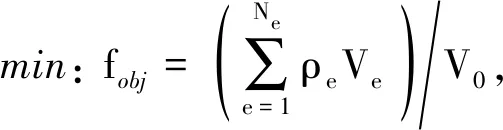
(6)
2 不确定性简谐激励下可靠性拓扑优化
2.1 简谐激励下可靠性拓扑优化模型
目前关于简谐激励下连续体结构拓扑优化的研究基本是在确定性条件下进行的,忽略了简谐激励的振幅和频率的不确定性对优化结果的影响。为了提高谐响应下结构的可靠性,设计满足指定可靠性水平的结构,本文在谐响应拓扑优化中考虑载荷振幅和频率的不确定性,建立了不确定性简谐激励下连续体结构可靠性拓扑优化模型,其数学列式为
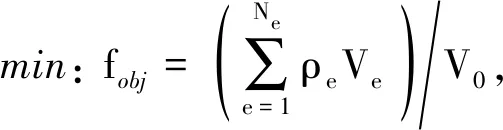
(7)
式中:X为不确定性简谐激励的振幅大小或频率随机变量;F(X)为随机简谐激励的振幅函数; 需要强调的是在式(6)定义的确定性优化模型中,结构的动刚度矩阵Kd和位移振幅u仅与设计变量ρ相关,而在式(7)定义的可靠性优化模型中,结构的动刚度矩阵Kd和位移振幅u为设计变量ρ和随机变量X的函数,受其二者影响;G(ρ,X)为用来度量结构可靠性的极限状态函数,定义为G(ρ,X)=Alimit-A,G(ρ,X)≤0表示结构失效;Pf为结构的失效概率,要求其小于或等于指定的失效概率Pf,t。可靠性模型中其他参数均与式(6)定义的确定性优化模型相同。
2.2 基于PMA的可靠性分析
在实际问题中,基于蒙特卡罗的方法计算失效概率的成本较大,为此,一些基于Taylor展开的数值近似方法相继被提出来处理式(7)中的可靠性约束,包括功能度量法(performance measure approach, PMA)[26-27]和可靠性指标法(reliability index approach, RIA)[28-29]。与RIA相比,PMA具有更高的效率和稳定性,因此本文使用PMA。基于PMA的谐响应可靠性拓扑优化列式表示为
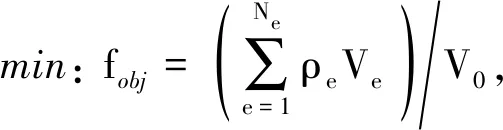
(8)
式中,Gp(ρ,X)为极限状态函数在目标可靠性曲面上的最可能失效点(most probable point, MPP)处计算的最小概率性能值,可以通过求解以下优化模型得到
min:G(ρ,Y)
s.t. ‖Y‖=βt
(9)
式中:Y为由随机变量X转化成的标准正态分布的随机变量;βt为目标可靠性指标,其与失效概率Pf,t之间关系为βt=-Φ-1(Pf,t),Φ-1为标准正态累积分布函数的反函数。通过求解式(9)得到的最可能失效点,记为Yp,则Gp=G(ρ,Yp)。
本文采用先进均值(advanced mean value, AMV)法查找求解式(9),寻找最可能失效点,其迭代格式为
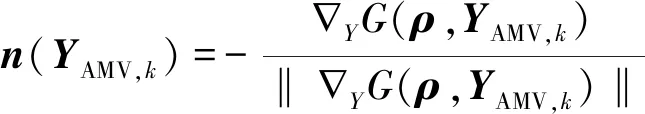
(10)
式中:YAMV,k+1为内层循环中使用AMV方法在第k+1次迭代中计算的随机变量值; ∇YG(ρ,YAMV,k)为极限状态函数关于随机变量Y的导数;n(YAMV,k)为G(ρ,Y)在YAMV,k处的归一化方向。
可以看出本文考虑简谐载荷振幅和频率不确定性的谐响应可靠性拓扑优化是嵌套的双循环优化算法,内层循环旨在寻找MPP,计算最小概率性能值Gp;外层循环更新设计变量ρ,形成新的结构。
3 灵敏度分析
由式(10)可知,寻找MPP需要计算极限状态函数对随机变量的导数。另外,为了能使用基于梯度的优化算法求解外层优化问题,需要计算极限状态函数对设计变量的导数,确定优化搜索方向。因此,本章实施灵敏度分析,详细推导极限状态函数关于设计变量和随机变量的导数。
3.1 极限状态函数对设计变量的导数
极限状态函数关于设计变量的导数可由链式法则推导得到
(11)
式中,导数项∂G/∂A可通过G(ρ,X)=Alimit-A直接求导得到
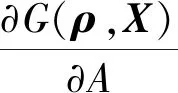
(12)
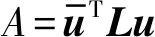
(13)
设随机简谐激励的振幅F与设计变量无关,式(5)两边同时对设计变量ρe求导可得
(14)
式(13)中导数项∂u/∂ρe可表示为
(15)
将式(15)代入式(13)可得
(16)
令伴随向量λ为式(17)定义的伴随方程的解
(17)
(18)
基于单元密度的拓扑优化方法通常会出现棋盘格现象。棋盘格现象是指单元密度为0或1的单元在设计域内交错布置的现象,使得优化后的拓扑结构的可制造性差[30]。为了避免棋盘格现象,获得清晰的黑白设计,本文采用以下敏度过滤方法对极限状态函数关于设计变量的导数进行过滤
(19)
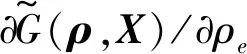
w(xj)=max(R-‖xe-xj‖,0)
(20)
式中,xe和xj分别为单元e和单元j的中心坐标。
3.2 极限状态函数对随机变量的导数
极限状态函数关于激励振幅随机变量z1和频率随机变量z2的导数由链式法则推导为
(21)
与导数项∂A/∂ρe的推导过程类似,导数项∂A/∂z1和∂A/∂z2可分别表示为
(22)
由于动刚度Kd与激励振幅随机变量z1无关, 载荷F与频率随机变量z2无关,式(5)两边分别对随机变量z1和z2求导可得
(23)
则式(22)中导数项∂u/∂z1和∂u/∂z2可分别表示为
(24)
将式(24)代入式(22)可得
(25)
同样令伴随向量λ为式(26)定义的伴随方程的解
(26)
(27)
本文采用Svanberg[31]提出的移动渐进线方法来求解式(6)和式(8)定义的优化问题。当内层迭代过程满足|Gk-Gk-1|≤10-6(Gk为极限状态函数在内层循环中第k次迭代的计算值)收敛条件时,内层迭代过程结束,进入外层拓扑优化,每一个拓扑优化迭代步都要进行内层逆可靠性分析循环,当外层拓扑优化达到最大迭代步数时,程序终止运行,本文算法的实施流程如图1所示。
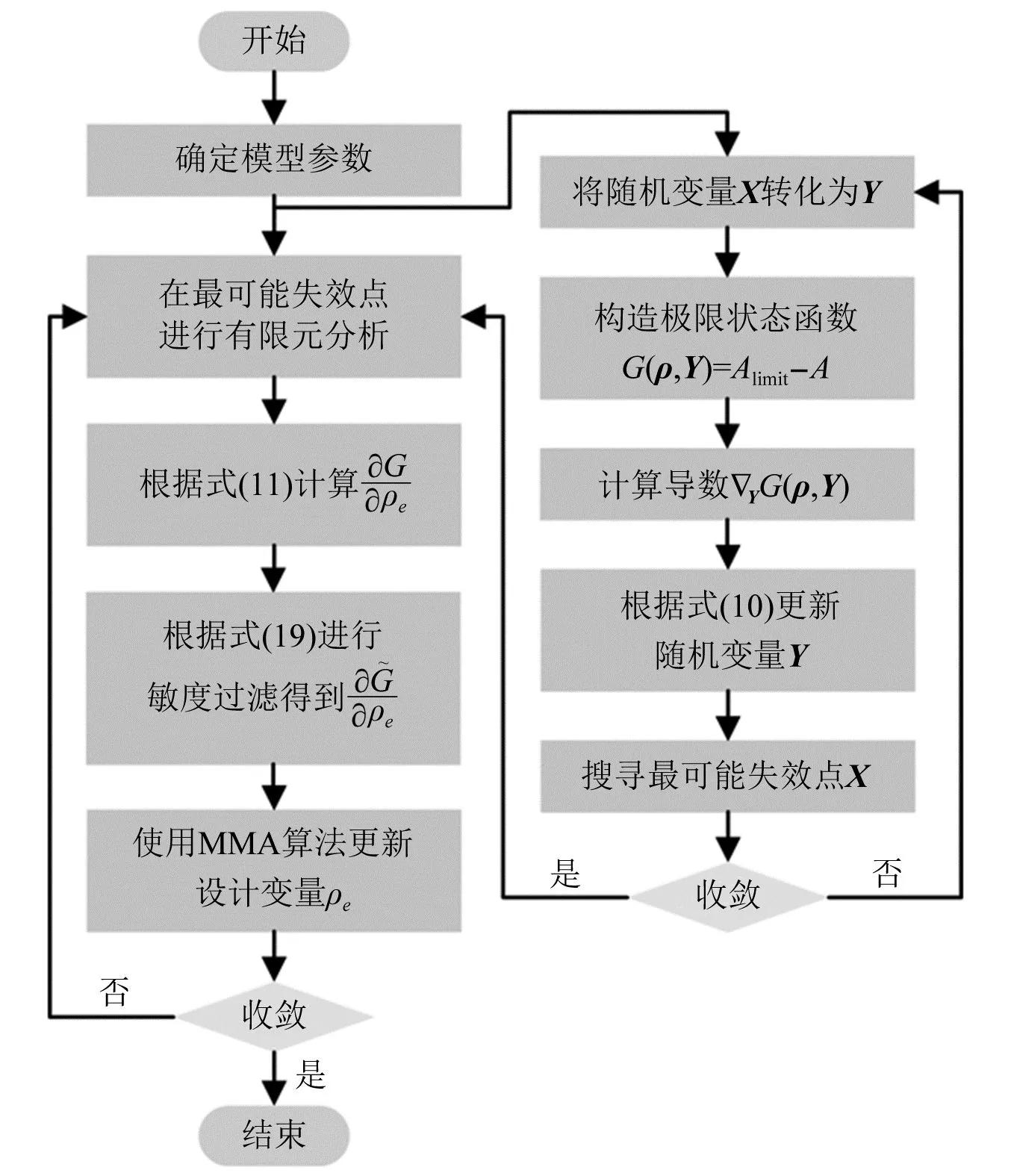
图1 本文算法的流程图Fig.1 Flowchart of the proposed algorithm
4 数值算例与讨论
本章通过两个算例来验证所提出的考虑简谐激励不确定性的谐响应可靠性拓扑优化方法的有效性。所有算例均使用相同的材料参数,假设材料弹性模量、泊松比和质量密度分别为210 GPa、0.3和7 800 kg/m3,阻尼系数cm=ck=1×10-4。简谐激励的振幅大小和频率均为服从正态分布的随机变量。设置所有设计变量ρe的初始值为1,最大迭代步数为300。
4.1 悬臂梁
悬臂梁结构尺寸如图2所示,设计域离散为240×80个边长为5 mm、厚度为1 mm的正四边形单元,左边界完全固支,右边界中部受竖直向下的随机简谐激励作用,振幅大小的平均值和标准差分别为1 000 N和100 N,频率的平均值和标准差分别为90 Hz和9 Hz。本算例将简谐载荷均匀分配到中间相邻的3个有限元节点上,以载荷作用点竖直方向的振幅平方和为极限状态函数来构造可靠性约束,设置约束限值为4.7 mm,过滤半径设为25 mm,目标可靠性指标为βt=2。
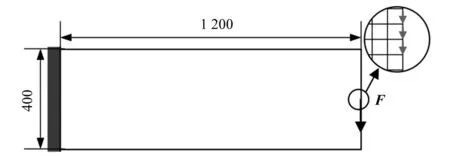
图2 悬臂梁结构示意图(mm)Fig.2 Illustration of cantilever beam(mm)
为了研究简谐激励的振幅大小和频率的不确定性对谐响应拓扑优化结果的影响,讨论以下4种不同情况。工况1:确定性载荷振幅大小和频率下的DTO结果,如图3所示,此时载荷振幅大小和频率分别为1 000 N和90 Hz。工况2:载荷振幅大小确定(取其平均值1 000 N),频率不确定下的RBTO结果,如图4所示。工况3:载荷频率确定(取其平均值90 Hz),载荷振幅大小不确定下的RBTO结果,如图5所示。工况4:载荷振幅大小和频率均不确定下的RBTO结果,如图6所示。
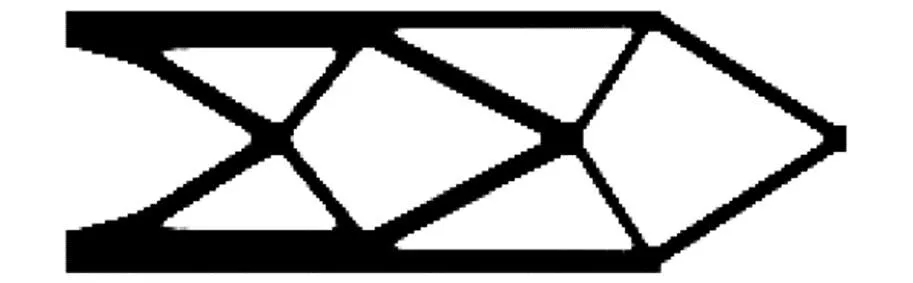
图3 确定性载荷振幅和频率下的DTO设计Fig.3 DTO design for deterministic load amplitude and frequency
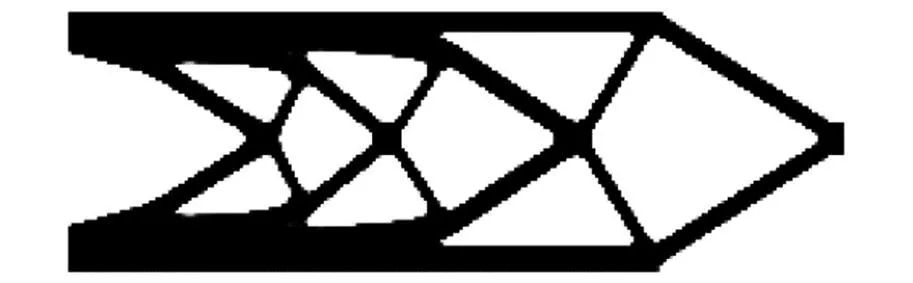
图5 确定性载荷频率、不确定性载荷振幅下的RBTO设计Fig.5 RBTO design for deterministic load frequency and uncertain load amplitude
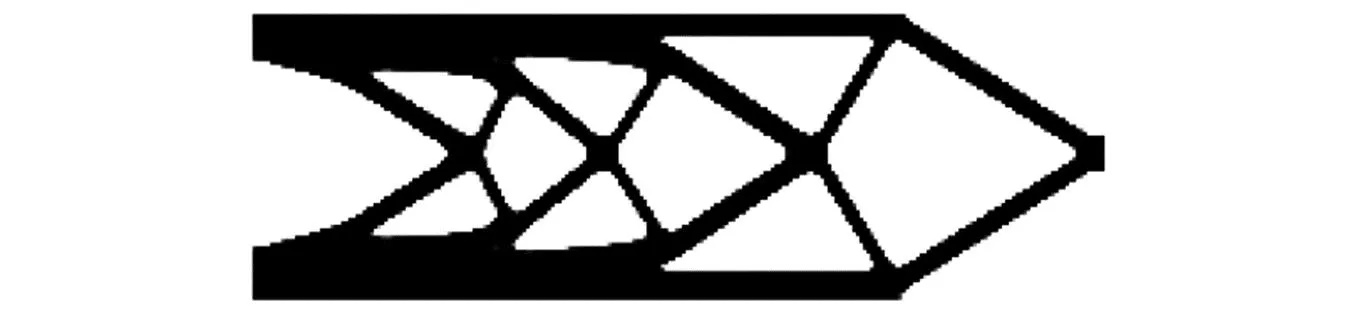
图6 不确定性载荷振幅和频率下的RBTO设计Fig.6 RBTO design for uncertain load amplitude and frequency
为了验证BRTO设计相对于DTO设计的优势,采用10 000个样本点对DTO和RBTO设计进行蒙特卡洛仿真。4种情况对应的结构体积比(目标函数),及蒙特卡罗可靠性指标,如表1所示。由表1可知:上述4种情况对应的结构体积比分别为31.90%、33.14%、39.20%和39.26%;对应的蒙特卡罗可靠性指标分别为-0.011 8、2.025 7、2.002 8和1.984 5。可以看出,3种RBTO设计均很好地吻合了目标可靠性指标βt=2,满足可靠性设计要求,最大相对误差不超过1.3%。与RBTO设计相比,DTO设计的可靠性水平(-0.011 8)相对较低。
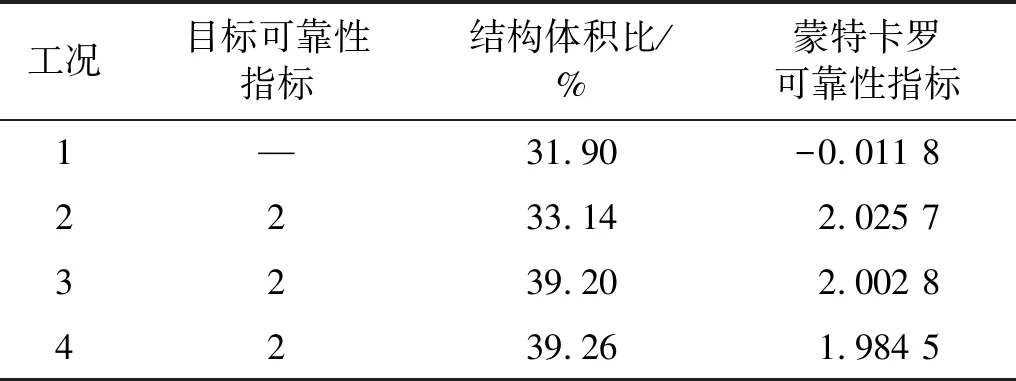
表1 不同情况下悬臂梁的优化结果
比较图3~图6可知,简谐激励下DTO设计与BRTO设计在拓扑构型上存在显著差异。与DTO设计相比,RBTO设计出现了更多的传力路径,材料消耗更多,更能满足可靠性设计要求。对比工况2~工况4可知,考虑载荷振幅不确定性的RBTO设计与只考虑频率不确定的RBTO设计相比,具有更大的结构尺寸和结构体积比。此外,考虑频率确定载荷振幅不确定的RBTO设计与考虑载荷振幅和频率均不确定的RBTO设计的拓扑构型基本相同,但后者结构体积比更大一点。
4.2 简支梁
简支梁结构尺寸如图7所示。设计域离散为320×40个边长为5 mm、厚度为1 mm的正四边形单元,底边两端点固支,上边缘中心位置处受到竖直向下的随机简谐激励作用。随机简谐激励的振幅大小的平均值和标准差分别为1 000 N和100 N,频率的平均值和标准差分别为100 Hz和10 Hz。以载荷作用点竖直方向的振幅平方为极限状态函数来构造可靠性约束,设置约束限值为0.5 mm,过滤半径设为15 mm。
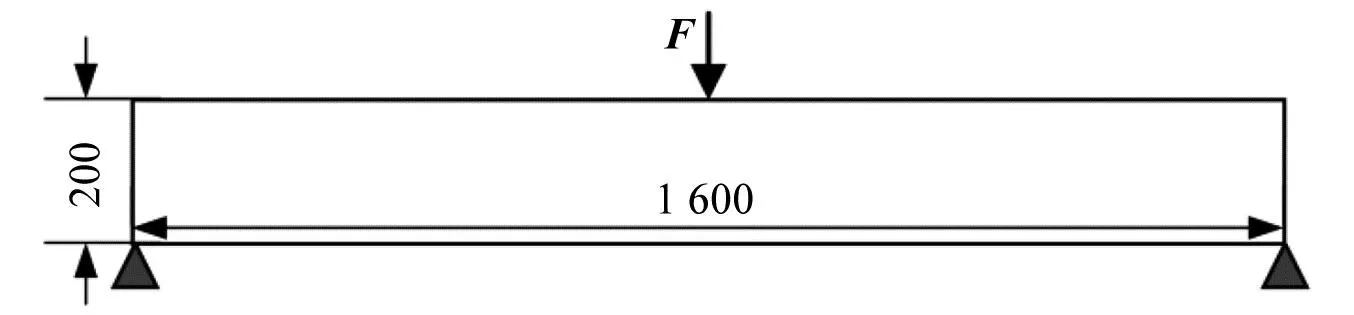
图7 简支梁结构示意图(mm)Fig.7 Illustration of simply-supported beam (mm)
为了研究不同目标可靠性指标对谐响应可靠性拓扑优化结果的影响,考虑载荷振幅和频率不确定性的谐响应可靠性拓扑优化方法在βt=1、2、3时的拓扑优化结果,如图8所示。由图8可知,3个不同目标可靠性指标对应的拓扑构型存在明显差异,其对应的结构体积比分别是37.14%、42.46%和49.07%。从优化结果来看,结构体积比随着可靠性指标取值的增大而增大,这说明谐响应下结构可靠性水平的提高需要消耗更多的材料。不同目标可靠性指标下固支梁的体积比迭代历史,如图9所示。由图9可知,3条迭代曲线都实现了稳定快速的收敛,证明了所提方法的稳定性。
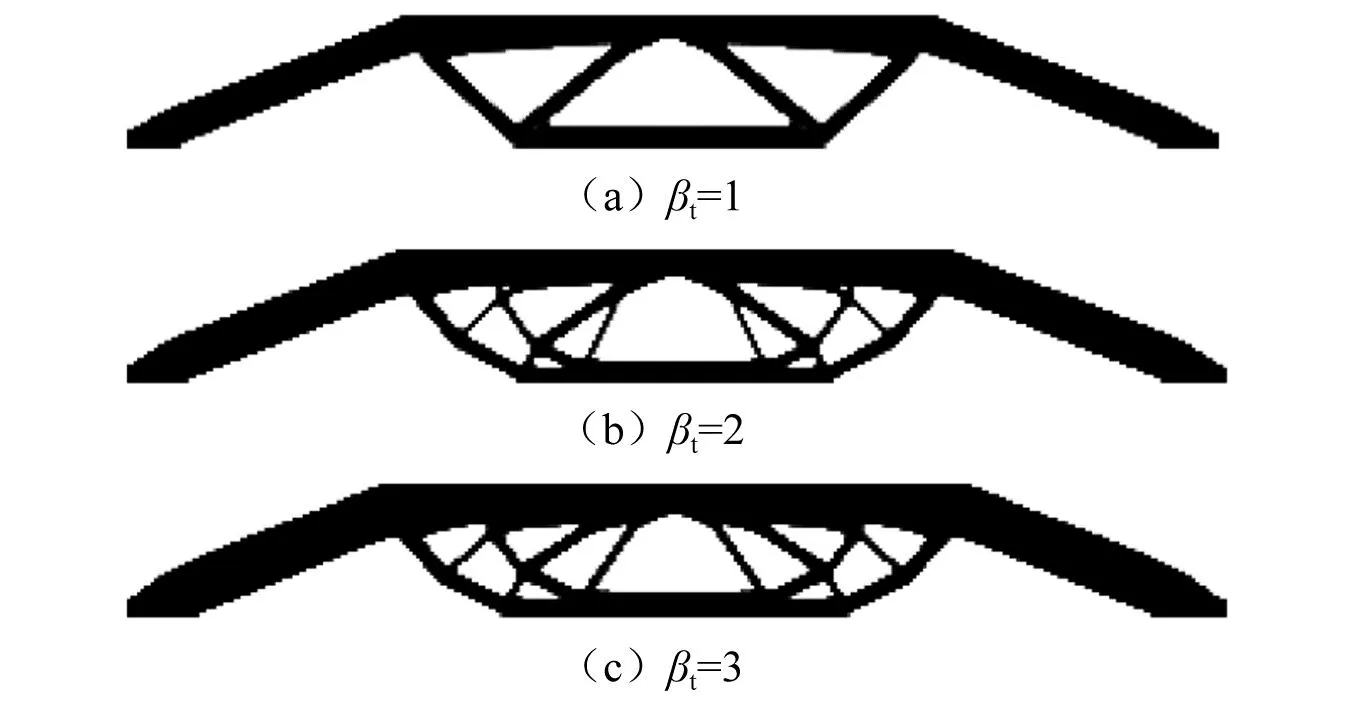
图8 不同目标可靠性指标下简支梁的RBTO结果Fig.8 RBTO results of simply-supported beam under different target reliability indexes
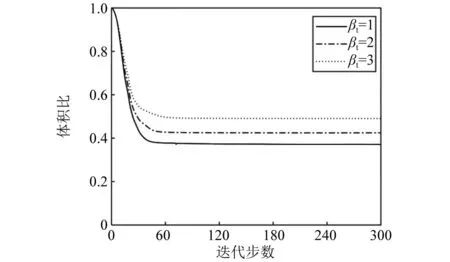
图9 不同目标可靠性指标下简支梁的体积比的迭代历史Fig.9 Iterative histories of volume fraction ratio of simply-supported beam with different target reliability indexes
为了验证本文谐响应可靠性拓扑优化方法的有效性,采用10 000个样本点对不同目标可靠性指标下的RBTO设计进行蒙特卡罗仿真,结果如表2所示。由表2可知,不同目标可靠性指标(βt=1、2、3)对应的蒙特卡罗可靠性指标分别为0.994 0、2.006 5、3.035 7,很好地吻合了目标可靠性指标,最大相对误差不超过1.2%。通过上述结果分析可知,考虑载荷振幅和频率不确定的谐响应可靠性拓扑优化方法能够有效设计出满足指定可靠性水平的拓扑结构。
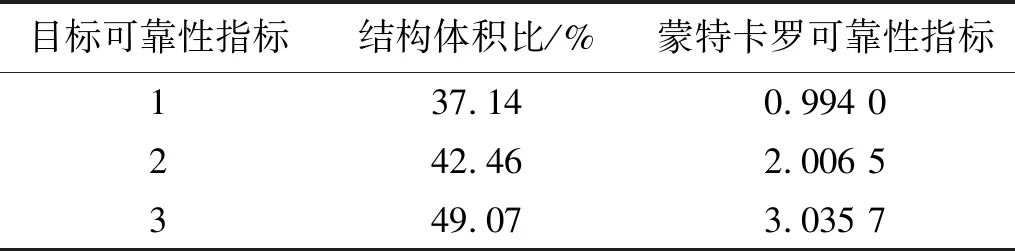
表2 不同目标可靠性指标下简支梁的优化结果
4.3 L型梁
L型梁的结构尺寸如图10所示。设计域离散为25 600个边长为5 mm、厚度为1 mm的正四边形单元,上边缘完全固支,右上端点受到竖直向下的随机简谐激励作用,振幅大小和频率的平均值分别为1 000 N和80 Hz。以载荷作用点竖直方向的振幅平方为极限状态函数构造可靠性约束,设置约束限值为1.7 mm,过滤半径R设为17 mm,目标可靠性指标为βt=2。
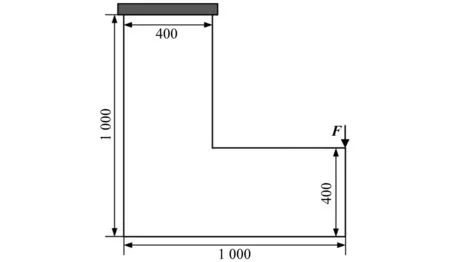
图10 L型梁结构示意图(mm)Fig.10 Illustration of L-shaped beam (mm)
为了研究随机简谐激励的振幅和频率的变异系数(coefficient of variations,COV)对谐响应可靠性拓扑优化结果的影响,考虑2个不同的变异系数(变异系数=标准差/平均值),即COV 取0.01和0.05。当COV为0.01和0.05时的RBTO结果,如图11所示。其对应的结构体积比分别是32.63%和35.65%。可以看出最终结构体积比随着随机变量的变异系数的增大而增大,这说明概率模型参数的变化对优化结果有影响。
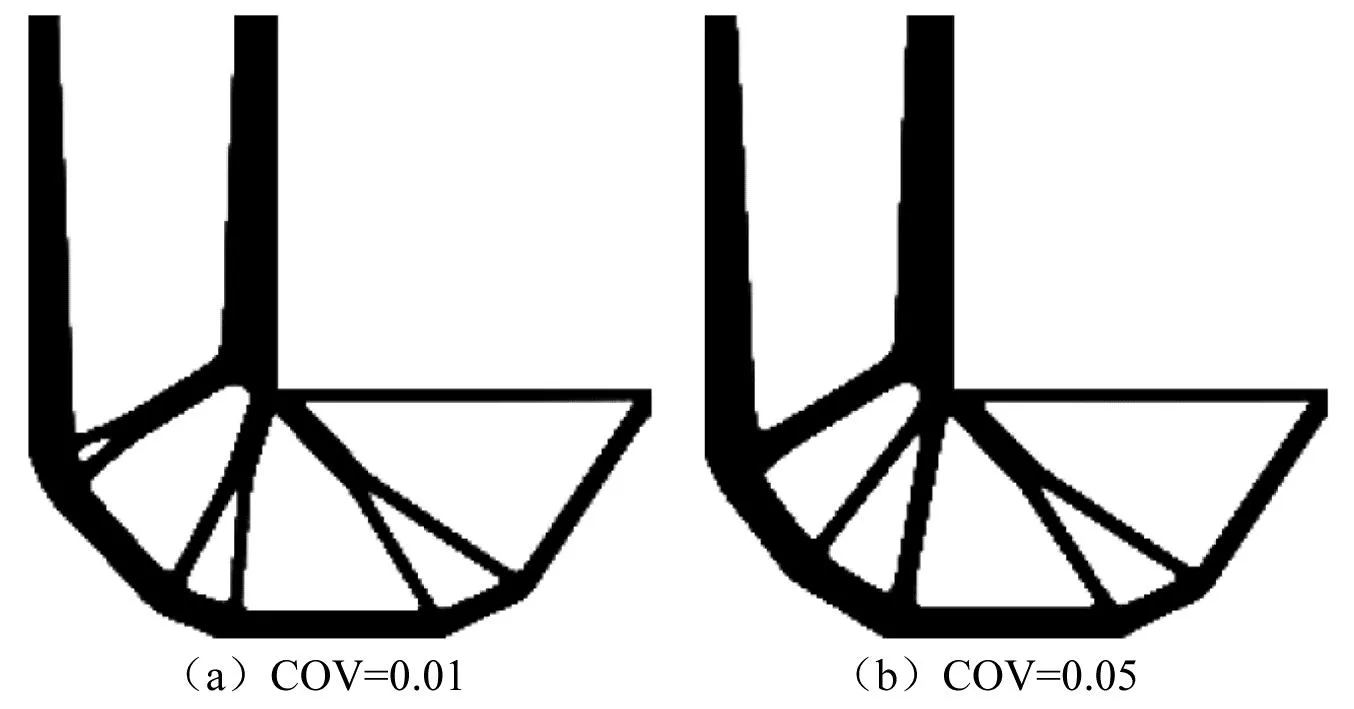
图11 不同变异系数下L型梁的RBTO结果Fig.11 RBTO results of L-shaped beam under different coefficient of variations
此外,采用10 000个样本点对L型梁在不同变异系数下的RBTO结果进行蒙特卡罗仿真,结果如表3所示。不同变异系数(COV为0.01、0.05)对应的蒙特卡罗可靠性指标分别为2.006 5和1.970 3,与目标可靠性指标βt=2的最大相对误差不超过1.5%,验证了RBTO结果的准确性,进一步说明了考虑载荷振幅和频率不确定的谐响应可靠性拓扑优化方法的有效性,可设计满足指定可靠性水平的动响应结构。
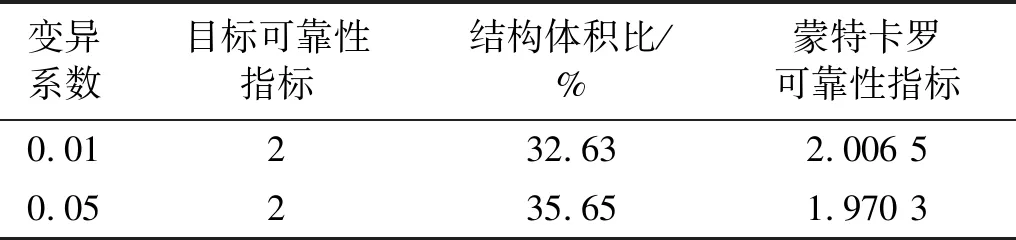
表3 不同变异系数下L型梁的优化结果
5 结 论
为了改善简谐激励作用下结构的使用安全性和可靠性,本文将考虑不确定性的可靠性分析理论整合到谐响应拓扑优化中,提出了一种有效的考虑载荷振幅和频率不确定性的谐响应可靠性拓扑优化方法。3个数值算例及蒙特卡罗仿真验证了所提方法的有效性,结果表明:
(1) 考虑不确定简谐激励的RBTO设计与DTO设计相比,结构拥有更多的传力路径,体积分数更大,可靠性水平更高,更能满足可靠性设计要求。
(2) 考虑载荷振幅和频率不确定性的谐响应可靠性拓扑优化方法能够有效设计出满足指定可靠度水平的结构。本文算例中,优化后结构可靠性指标与目标可靠性指标之间的最大相对误差不超过1.5%。
