智能阀门定位器非线性特性与建模问题研究

严涛

江苏圣泰阀门有限公司 江苏 盐城 224001

气动调节阀在工业生产中具有重要的作用，由于自身的结构特点，此类阀门的定位器在使用过程中存在非线性特性，即输入信号达到一定阈值后才能引起阀位动作，在一定程度上限制了阀门的调节性能。研究该特性的具体成因，建立相关的运动模型，有利于进行优化设计，故对其展开研究。

1 阀门定位器非线性特性测量与建模

1.1 饱和非线性特性建模

1.1.1 饱和非线性特性的表现形式

饱和非线性用于描述控制信号和输出信号的某种特定关系，假设存在一个阈值，当控制信号大于（小于）阈值时，输出信号发生变化，反之则输出信号维持不变，其形成条件较为特殊，仅短时出现，但是却能显著影响控制系统。

1.1.2 阀门定位器饱和非线性特性描述

研究过程以AVP301阀门定位器为分析对象，根据其结构特征，有可能引起饱和非线性特性的部位包括两个，其一为气动放大器，其二为力矩马达的喷嘴-挡板[1]。

喷嘴-挡板结构由背压腔、喷嘴、挡板以及感应磁体等组成，气源通过节流孔进入背压腔，再通过喷嘴射向挡板，当气源压力Ps保持不变时，气源压力和背压腔之间的压力比值满足公式（1）。

式中：Pb表示背压腔的压力；D为喷嘴的孔径；d为节流孔的孔径；Cf1、Cf2分别为节流孔和喷嘴的流量系数；a为喷嘴-挡板结构的空间距离。参数D、d为恒定值，当气源压力保持恒定时，Cf1、Cf2同样为定值，Ps保持不变，则Pb仅与参数a相关，虽然参数a具有一定的调节空间，但不能无限改变，因此压力Pb具有非线性特性。

气动放大器用于放大气源信号，当气体流量或者压力非常小时，可通过放大器输出放大后的信号，其组件包括阀芯、上腔盖、上膜片、中膜片、下膜片、下腔盖等[2]。式（2）为气动放大器进气或排气时的信号特征。

式中：Pb为式（1）中的背压腔压力；Ps为气源压力；Pout为输出气压；S1、S2、S3为上、中、下膜片的面积。S1、S2、S3为恒定值，不会引起Pout的变化，当气源压力Ps维持不变时，Pout的输出结果仅受到参数Pb的影响，由于参数Pb具有非线性特征，进而导致Pout也具备非线性特性。

1.1.3 阀门定位器饱和非线性特性测量

为了测量阀门定位器的饱和非线性特性，研究过程建立了专门的实验模型，称为CVM（Control Valve Model）模型，由气动放大器、I/P转换、智能控制器组成，其中I/P转换用于模拟喷嘴-挡板结构。为了提高CVM模型的精确性，进一步丰富了测量系统的组件，基于CVM模型的改进测量系统由气罐、AVP301阀门定位器、压力变送器、板卡、机箱组成。在该实验模型中，阀门定位器开环系统的工作原理如图1所示。

图1 阀门定位器饱和非线性特性测量开环系统框图

在上图中，Iop为设定输入的电流值，Ps为气源气压（保持稳定），Pb为模拟的背压腔压力，Pout为输出气压。

在实验过程中，通过Iop与Pout之间的关系判断Iop与Pb的关系，进而确定线性区域和非线性区域，电流信号Iop的取值范围在0.250～0.480mA之间，气源压力设定为三个取值，分别为200、350、500kPa，在给定电流区间内，以连续阶跃的方式提高电流信号的强度，持续时间为300s，观察Pout的输出结果。表1为200kPa时的实验数据。从数据可知，当Iop电流信号在0.250～0.275mA和0.450～0.480mA时，Pout基本维持不变，属于非线性特性区间；当Iop电流信号在0.300～0.425mA时，Pout呈线性增长，属于线性区间。另外两组实验中同样观察到了线性区间和非线性区间。

1.2 间隙非线性特性分析

当智能调节阀系统达到稳定状态之后，气室气压有可能缓慢减小，在这一过程中，阀位先维持稳定，当气压下降幅度足够大时，阀位才会出现明显的变化，以上过程称为间隙迟滞模型。间隙非线性特性是一个误差模型，用于描述输入值、间隙位置和输出信号之间的关系[3]。间隙特性的产生具有多方面的原因，包括喷嘴和挡板之间存在距离以及调节阀杆和填料之间存在摩擦作用力。以摩擦力的影响为例，当填料和调节阀杆的摩擦力过大时，填料会紧密地挤压填料盖，由此引起二者之间的粘滞现象，进一步引起间隙非线性特性。

2 调节阀实验平台摩擦力模型构建

2.1 摩擦力模型构建

调节阀要求密封阀体和阀杆，密封材料称为填料，通常可使用聚四氟乙烯进行密封处理，而填料的应用产生了摩擦力，成为导致间隙非线性特性的重要原因，智能阀门定位器可用于消除这一特性，提高调节阀的准确性[4]。调节阀气动执行机构的运动规律如式（3）。

式中：Pc为气动室的压力；A为气动室的截面积；Ftotal为各类摩擦力之和；K为弹簧的弹性系数；x为弹簧的运动距离；x'为弹簧的运动速度；x"为弹簧运动的加速度；m为阀杆和阀芯的总质量；b为间隙[5]。在以上关系式中，当阀杆运动速度不为0时，摩擦力Ff=fc+fv·c，其中fc为库仑摩擦力，fv为粘滞系数。当阀杆运动速度为0时，Fs=fs，此处fs表示阀杆受到的最大静摩擦力。在式（3）中，mx"可按照式（4）进行计算。

式中：Fr为弹簧的弹力；Fa为调节阀气室动力；Ff为阀杆受到的摩擦力；Fu为系统的不平衡力；Fp为预紧力。通过式（2）和式（4），可推导出实验平台摩擦力模型的数学表达式，见式（5）。

2.2 模型参数实验

为了提高模型的精确性，应该通过实验确定各个参数的取值。以最大静摩擦力试验为例，在实验装置中输入低频率的正弦电流信号，P1表示电流波峰处的气室压力，P2为电流波谷处的气室压力，X1对应电流波峰处的弹簧位移，X2为电流波谷处的弹簧位移，阀杆受到的最大静摩擦力fs=[（P2-P1）×A-（X2-X1）×K]/2，实验数据见表2，求出10次实验中fs的平均值，则有fs=131.585N。另外，经过实验，动摩擦力的均值为128.992N，弹簧刚度的实验结果为213295N/m。

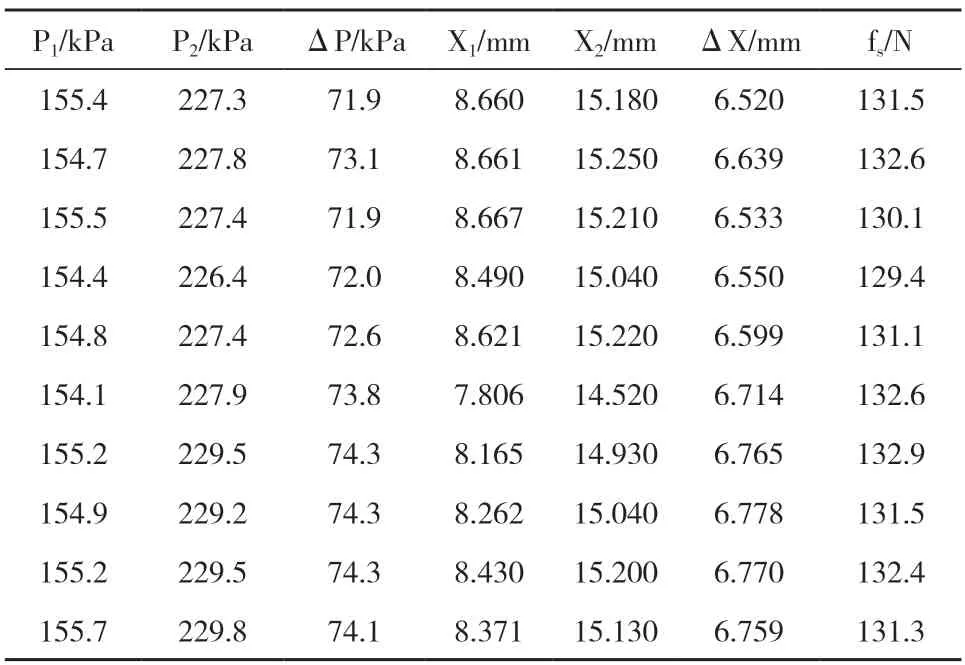
表2 阀杆最大静摩擦力试验数据

2.3 模型验证及结果分析

模型验证的目的是评价改进的CVM模型和真实的智能阀门系统的相似度，针对两套系统分别开展斜坡实验，电流输入信号先从0提高至0.8mA，再从0.8mA降至0mA，气源压力设置为350kPa，电流信号输入总时长为650s。对比观察CVM模型的阀位与真实阀位之间的误差，结果如表3所示。从数据可知，电流信号为0.310、0.315mA时，属于非线性特性区间，电流信号在0.320～0.390mA时，属于线性区间，电流信号为0.400、0.410mA时，再次进入非线性特性区间。改进CVM模型的阀位与真实阀位高度接近，误差也非常小。

表3 模型小阶跃信号实验结果

3 研究结果讨论

经过理论分析和检测，证明了智能阀门定位器确实存在非线性特性，对于此次所研究的AVP301型阀门定位器，非线性特性的产生与喷嘴-挡板结构的运行过程存在关联，气压放大器的输出压力受到背压腔压力的影响，也具有非线性特性。

研究过程设计了能够模拟调节阀执行结构运动规律的实验模型，上文中称为CVM模型，并对其进行了优化和改进。该改进的CVM实验平台为基础，建立了实验系统的总摩擦力模型，对其中的关键参数进行检测，从而确定了具体的取值，包括阀杆最大静摩擦力、弹簧刚度等。

针对优化的CVM模型，将真实的调节阀系统作为对照组，对比两种系统的偏差，发现改进的CVM模型与真实的调节阀高度接近，误差非常小，可作为研究调节阀的高精度模拟装置。

4 结语

针对智能阀门定位器的非线性特性，研究过程分析了饱和非线性特性和间隙非线性特性的具体成因，确定了气动放大器和动力马达的喷嘴-挡板机构是引起该特性的主要原因。为了进行模拟，设计出CVM模型，使用改进的CVM模型测量阀门定位器的饱和非线性特性，并且对比该模型与真实的智能气动调节阀对小阶跃信号的响应情况，结果显示，改进的CVM模型能够准确检验出非线性特性。