V-H-M复合加载模式下三桩基础的失效包络面研究
2024-04-11赵子豪张皓杜威张正飞张海旭
赵子豪, 张皓, 杜威, 张正飞, 张海旭
(1.沈阳建筑大学 土木工程学院, 辽宁 沈阳 110168;2.河海大学 岩土力学与堤防工程教育部重点实验室, 江苏 南京 210098;3.中冶沈勘工程技术有限公司, 辽宁 沈阳 110169;4.中建铁投路桥有限公司华中分公司, 江西 南昌 330038)
0 引言
大力开发和利用海洋风能是我国重要的能源战略选择。近年来,海上风力发电产业迅速发展,随着风电场场址水深与装机容量的不断增加,传统的单桩式基础逐渐不能满足承载力的需求,因而各类其他基础形式相继出现。采用三桩基础与上部导管架衔接可以提高结构物的整体性,增强其抗倾覆能力,被认为是一种高效的桩基础形式。
目前学者和工程师们对三桩基础的受荷行为进行分析设计时常常仅针对桩基础本身[1],而忽略了三桩基础地基失效破坏的可能性,然而很多基础结构的失稳破坏是由地基承载力不足引起的,三桩基础地基承载力的研究同样关键。Zhao等[2]采用数值分析方法和极限分析上限解法得到了水平荷载作用下三桩基础的极限土抗力平面应变解答,并考虑距径比的影响构建了适用于不同距径比条件的理论破坏机制,然而只考虑独立的水平荷载条件并不能反映三桩基础受力的复杂性。
由于海上风机塔筒通常体型巨大且高耸,其在海洋上所处的力学环境又十分恶劣,因此长期受到风、海浪等瞬时或循环的水平荷载作用。该水平荷载通过上部结构传至基础顶面,导致三桩基础在承受自身的竖向荷载V的同时,还要承受巨大的水平荷载H和弯矩荷载M作用,因此考虑不同的加载条件,开展复合加载模式下的三桩基础地基的承载力稳定性研究尤为重要。
破坏(失效)包络面理论[3-5]是反映复合加载模式下各类基础承载力大小的重要理论。在不同荷载分量组成的坐标空间内,可以根据荷载分量所对应的点与破坏包络面的相对位置关系判断基础的稳定性。刘润等[6]基于ABAQUS有限元软件讨论了海上风电筒型基础在复合加载模式下的地基承载力和破坏模式,并通过试验验证了数值分析结果的可靠性。李思琦等[7]针对非共面V-H-M复合加载模式下桶形基础的承载特性展开研究,其研究成果与范庆来等[8]提出的公式进行了比较,结果相近,并提出非共面V-H-M复合加载模式下破坏包络面的方程。Graine等[9]通过极限分析法研究了黏土中单桩在三维空间中的破坏包络面特性,得到在V-H-M空间中失效包络面和经验表达式,同时Graine等[10]、Leng等[11]还探讨了土的摩擦角、黏聚力、单位质量及桩的布置形式等因素对破坏包络面的影响。Zhao等[12]采取极限分析法对复合加载模式下的双桩基础的破坏机制进行了系统的研究,同时还确定了V-H-M共同作用下双桩基础的破坏形态及失效包络面,并根据失效包络面得到了判断承载特性的经验表达式。由此可见,运用数值手段对不同形式基础的失效包络面进行研究评价是一种切实有效的途径,然而遗憾的是,目前针对三桩基础复合加载模式下的承载力研究还不够完善,仅有刘冰雪[13]对V-H平面下三桩基础的耦合承载力进行了研究分析。
基于以上,本文将针对海上风机三桩基础,根据失效包络面理论采用有限元极限分析方法,对V-H-M复合加载模式下的承载力特性展开研究,讨论三桩基础地基的失效机制。同时考虑不同深径比与距径比条件对三桩基础失效包络面的影响,最终形成三桩基础三维失效包络面的经验表达式,为指导工程实际提供有效的依据。
1 问题描述
V-H-M复合加载模式下的三桩基础如图1所示。由图1可见,三桩基础呈等边三角形布置,置于均质黏土地基中,其中桩深为L,桩径为D,桩间距为s,黏土体的容重为γ,不排水抗剪强度为su。3根桩桩顶由刚性桩帽连接,桩帽距土体表面距离为1倍桩径。所有荷载(竖向荷载V、水平荷载H和弯矩荷载M,符号上标代表了荷载的作用方向,“+”代表沿坐标轴正方向,“-”代表沿坐标轴负方向)均施加于桩帽上并作用于同一平面内。本文所用到的荷载及符号约定与Gottardi等[14]文中保持一致,荷载符号规定见表1。黏土体采用基于Tresca屈服准则的理想弹塑性本构模型,桩身和桩帽则模拟为完全刚性材料并不考虑桩身自重,桩土界面处于完全粗糙状态。需要说明的是,在Tresca模型中材料的不排水抗剪强度su是唯一强度指标,后续分析对荷载结果进行了无量纲化处理(V/suD2、H/suD2、M/suD3),以考虑材料强度对极限荷载及失效包络面结果的影响。
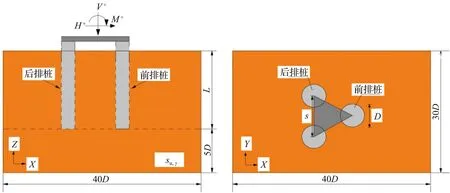
图1 V-H-M复合加载模式下的三桩基础Fig.1 Tripod pile foundations under combined V-H-M loading

表1 荷载符号规定Tab.1 Load symbol specification
2 有限元分析模型
有限元极限分析(finite element limit analysis, FELA)方法是一种能高效预测岩土结构稳定性的新型数值计算手段。该方法的优势在于它在满足极限分析上下限理论的基础上,结合了数值离散化的思想,对解决复杂几何条件和边界条件的问题有很好的适用性,同时,它还可以通过加密单元的方式使得上限解UB不断逼近下限解LB,得到更高精度的极限荷载解答。根据Graine等[9]的描述,最大分析误差Eerr定义如下:
(1)
2.1 模型尺寸及材料参数
本文中研究基于有限元极限分析软件OPTUMG3建立三桩基础复合地基的三维有限元模型(图2)。考虑到模型网格的对称性特征,此处仅选取模型的1/2进行展示。所有三桩复合地基统一采用长度为40D、宽度为30D、高度为L+5D的长方体模型进行描述。通过对模型尺寸的敏感性分析可知,所用模型尺寸可在保证计算效率的同时,有效避免边界效应对计算结果的影响。模型的边界约束采用标准边界条件,其中底面与侧面约束法向位移,而顶面自由。由于本研究中不考虑基础结构本身的变形与破坏,因此桩体与桩帽被简化为无自重的刚体材料,桩径D取值为1 m,深径比L/D取值分别为3、6、9,同时距径比s/D取值分别为2、4、6。土体被视为理想弹塑性材料,并服从Tresca屈服准则,其中土体容重γ取值为20 kN/m3,土体弹性模量Eu取值为30 MPa,泊松比υ取值为0.495,土体不排水抗剪强度su取值为50 kPa。本文在模拟桩-土接触面时采用了拉伸截断的Tresca模型,最大剪应力与土体的不排水抗剪强度保持一致,可以很好地模拟受荷中桩后空隙的出现。
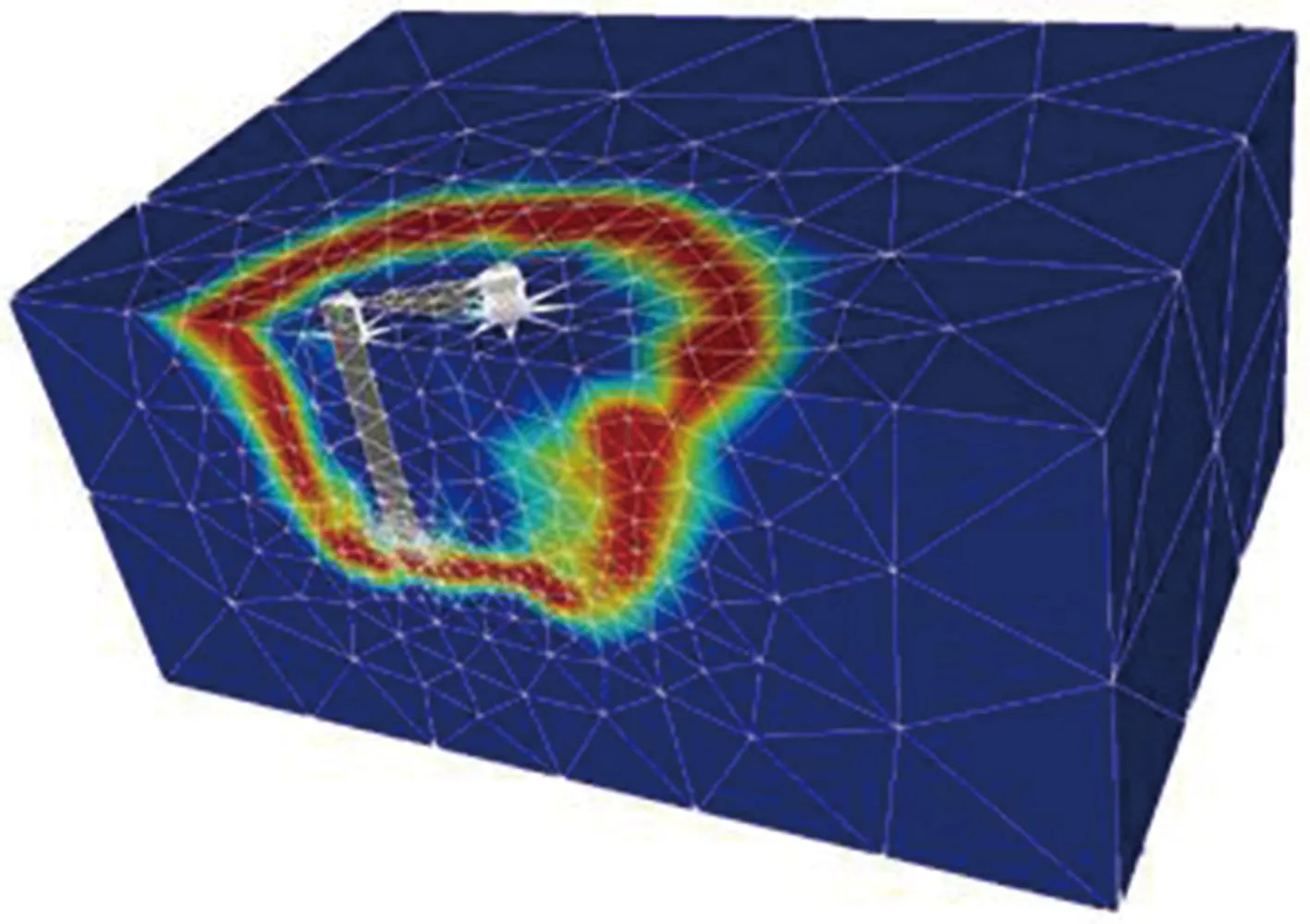
图2 复合地基的三维有限元模型Fig.2 3D finite element model of the coupled foundation
2.2 网格划分及自适应技术
三桩基础有限元模型中的桩身和土体均采用四面体实体网格进行划分(图2),顶部桩帽采用无厚度的刚性板单元进行模拟,而桩-土接触面则采用剪切节理单元进行描述。为了保证分析结果的精确性,本研究在进行数值计算时还启用了 OPTUMG3软件中自有的网格自适应技术。该技术可以在每个计算步内将网格自动加密,通过确定适当的初始网格数量和自适应计算步,可以得到精度满意的结果。网格数量对极限承载力的影响见表2。初始网格数量和优化网格数量越多,求解的结果精度越高,当初始网格达到3 000和优化网格达到15 000时,计算精度的提高并不明显,因此,在本研究中,三桩有限元模型将使用3 000个初始网格,经过3次自适应加密计算最终获得15 000个优化网格(如图2所示)。经测算该网格精度下的结果可以满足分析需要。

表2 网格数量对极限承载力的影响(L/D=9和s/D=6)Tab.2 Influence of grid number on ultimate bearing capacity(L/D=9 and s/D=6)
2.3 复合荷载加载方法
本文通过固定荷载比的加载方法获得三桩基础在V-H-M复合加载模式下的失效包络面。该加载策略在固定V条件下将H和M设置为乘数荷载,通过保持H/M比值(H/M=tanα)的大小不变加载至失效极限值,此时加载轨迹将收敛于H-M平面中失效包络线上的某点,然后通过改变H/M比值,进而获得多条加载轨迹和多个离散点,最终得到该V条件下的H-M平面失效包络线,如图3所示。
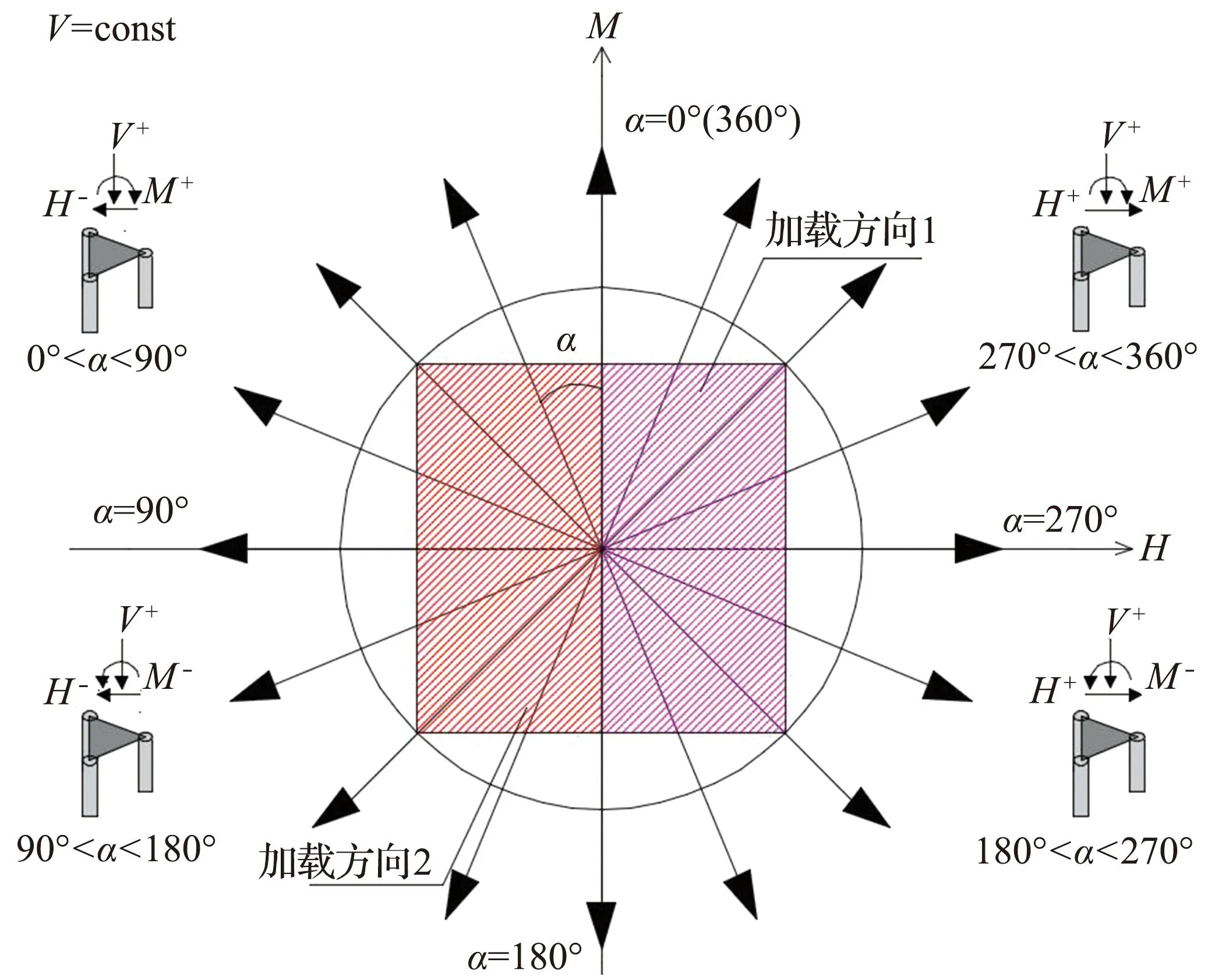
图3 固定V水平下的H-M平面加载路径Fig.3 H-M plane loading path at fixed V level
通过整合不同竖向荷载水平下的失效包络线,最终获得V-H-M复合加载模式下的三维空间包络面。为了保证包络面的完整性,本文共考虑了7种竖向荷载水平(即V=0、0.25V0+、0.50V0+、0.75V0+、0.85V0+、0.90V0+、0.95V0+),因此,三维空间内单个失效包络面需要进行约350次模拟才能完整获取。需要说明的是,由于三桩基础在实际服役时的竖向荷载主要来源于上部结构自重,因此本文只研究了压缩荷载对基础耦合承载行为的影响。同时考虑到自重荷载的大小相对固定,本文中所采用加载方法良好反映了三桩基础的实际受荷特性。
2.4 模型验证
为了验证有限元极限分析模拟方法及所建模型的可靠性,本文分别按照文献[15-19]和文献[13]中单桩和三桩基础的几何尺寸及土性参数建立了相应的数值模型。表3给出了本文单桩单向承载力结果与已有结果的对比,其中Vult、Hult分别表示单桩基础单向加载条件下的极限承载力。由表3可以看出:本文无量纲化处理后的竖向承载力结果与文献[15-19]的结果十分近似,最大偏差小于8%,满足对比分析的精度要求;本文水平承载力结果与文献[17,19]的结果相近,同时小于文献[18]得到的理论上限解,故产生的误差是可以接受的。基于以上分析可知,采用有限元极限分析方法模拟桩基承载力问题是可行的。三桩基础竖向及水平承载力与前人文献的对比见表4。从表4可以看出,本文获得的三桩基础的单向加载承载力计算结果与文献中[13]所记录结果之间的差异也在合理范围之内,进一步证明了所建三桩基础模型的可靠性。

表3 单桩基础竖向及水平承载力与前人文献的对比Tab.3 Comparison of vertical and horizontal bearing capacity of a pile foundation with the previous literature

表4 三桩基础竖向及水平承载力与前人文献的对比Tab.4 Comparison of vertical and horizontal bearing capacity of tripod pile foundation with the previous literature
3 三桩基础失效包络面
3.1 单向加载条件下的极限承载力
在构造三桩基础三维空间中的失效包络面之前,本文首先采用有限元极限分析软件OPTUMG3中不同的单元类型(上限解UB单元、下限解LB单元和混合解MG单元)对三桩基础在各单向加载条件下(V、H和M)的极限承载力进行求解。为了使分析结果具有普遍适用性,所得极限承载力均以无量纲化的形式进行表达,如图4所示。其中大多数工况下上限解与下限解之间的误差小于5%,最大误差小于8%,满足分析结果的基本精度需要。通过3种结果的对比分析可以看出,混合解均介于上、下限解之间,更接近极限荷载的真实解,因此,在之后复合加载模式下失效包络面研究中,分析结果均以混合解的形式呈现。另外,图4进一步考虑了三桩基础不同的几何尺寸(深径比L/D和距径比s/D)与加载方向(沿坐标轴正方向和反方向),可以发现,当深径比和距径比增大时,三桩基础的各单向承载力均不同程度地增大。此外加载方向对基础的横向(H和M)承载力有一定影响:在距径比较小时(s/D=2),沿坐标轴正方向和反方向加载时得到的极限承载力数值相差很小,随着距径比的增大,二者的差值相应增加。这是由于三桩基础在水平受力的正交方向上的几何特征是非对称的,因此当加载方向发生180°旋转时每根桩分配的极限土体抗力是不同的,进而得到了相异的横向承载力。由此可知,对于大距径比的三桩基础,加载方向对极限承载力的影响是不可忽视的。另外图4还包含了文献[11]关于其他形式群桩基础(例如双桩与四桩基础)极限承载力的分析结果,可以获得合理的变化规律:随着多桩基础中桩数的增加,极限承载力不断增大。



图4 单向加载条件下的极限承载力Fig.4 Ultimate bearing capacity under unidirectional loading
3.2 H-M平面失效包络线
复合加载模式下,三桩基础失效包络面在H-M平面坐标系中上的投影(即H-M平面失效包络线)可以反映固定竖向荷载水平下弯矩荷载对基础水平承载力的影响规律。本文首先不考虑竖向加载V作用对失效包络面的影响。
图5表示的是当V=0时对应L/D=6且s/D=4的三桩基础在H-M平面上的失效包络线。该曲线大致呈中心对称的一个倾斜椭圆,在第一、三象限中呈现为一条近似线性变化的直线,而在第二、四象限中呈现为包含极值点(P2和P2′)的曲线。失效包络线关于纵轴分割的两段曲线(图5中的实线与虚线)反映了加载方向(H>0与H<0)对三桩基础失效行为的影响。由图5可知,虽然两端曲线的变化趋势大致相同,但对应不同加载方向的曲线极值大小是有差别的,P2′所对应的最大水平承载力比P2所对应的值大约180 kN。
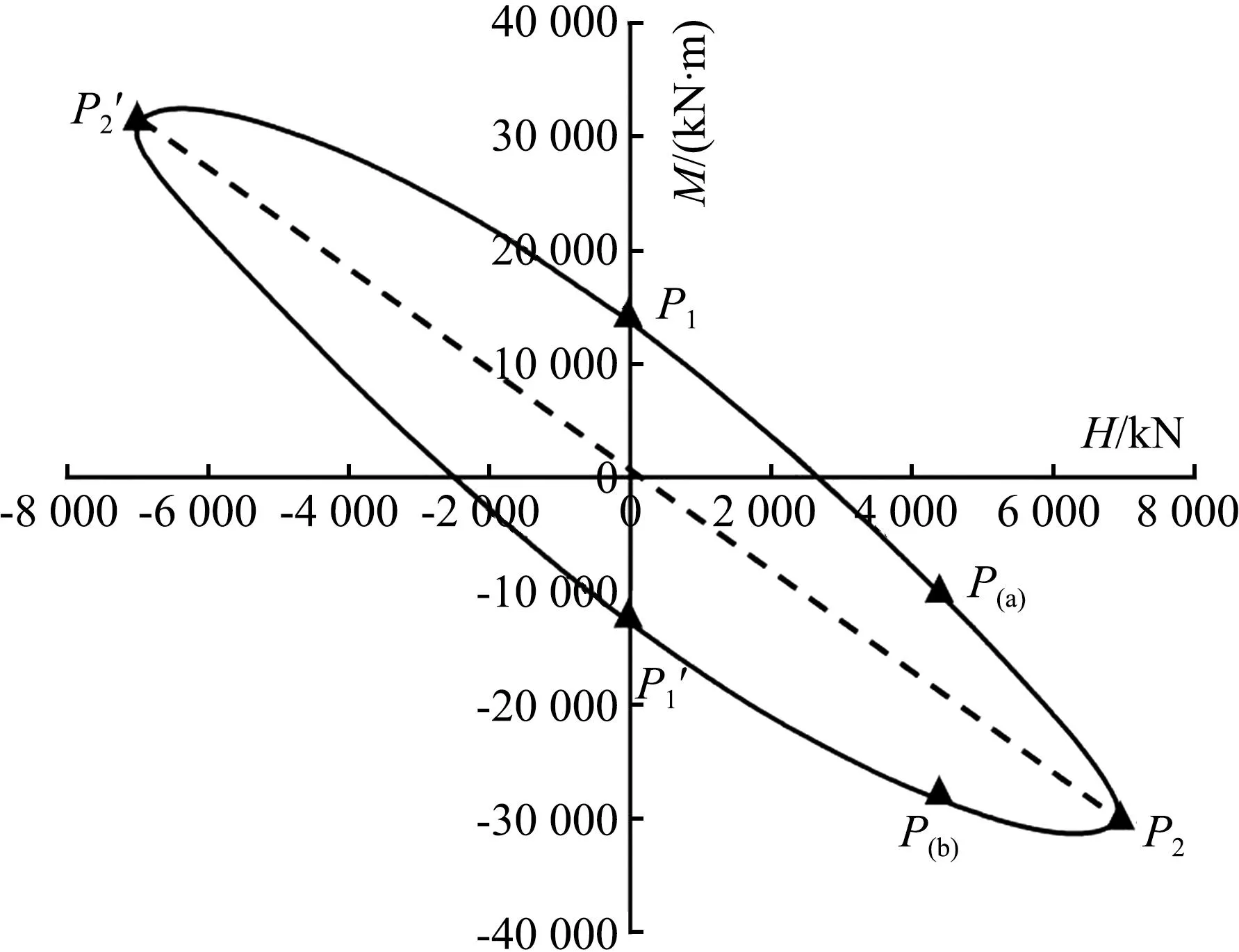
图5 L/D=6和s/D=4时,H-M空间失效包络线Fig.5 Failure surfaces in the H-M loading space for L/D=6 and s/D=4
当HM>0(即图5的第一、三象限)时,弯矩荷载与水平荷载的加载作用使桩基有相同方向的位移趋势,此时弯矩荷载的增加会加速桩-土体系的倾覆破坏,进而使体系所能承受的最大水平力减小。而当HM<0(即图5的第二、四象限)时,弯矩荷载与水平荷载的加载作用使桩基有相反方向的位移趋势。在此阶段桩-土体系所能承受的极限水平力随着固定加载比M/H的改变先增大后减小,体系的最大水平承载力在曲线转折点(P2与P2′)处获得。在转折点之前,由于加载比M/H偏小,此时水平荷载是决定三桩基础倾覆失效的主要荷载分量,而弯矩荷载的存在将会抵抗桩-土体系的倾覆移动趋势,因此M的增加会使体系的水平承载力增大。而在转折点之后,随着M/H的增大,弯矩荷载会逐步成为桩-土体系失效的主导荷载,因此体系所能承受的最大水平力分量减小。L/D=6和s/D=4时剪切耗散如图6所示。由图6可以看出,从桩-土体系的失效机制上看,在转折点之前,三桩基础的运动方向与H的加载方向相同,极限状态下桩体前侧的土体中将会产生较多的剪切耗散[如图6(a)]。而在转折点之后,受弯矩增加的影响三桩基础的运动方向发生倒转,与H的加载方向相反,极限状态下剪切耗散相对均匀地分布在三桩基础周围[图6(b)]。
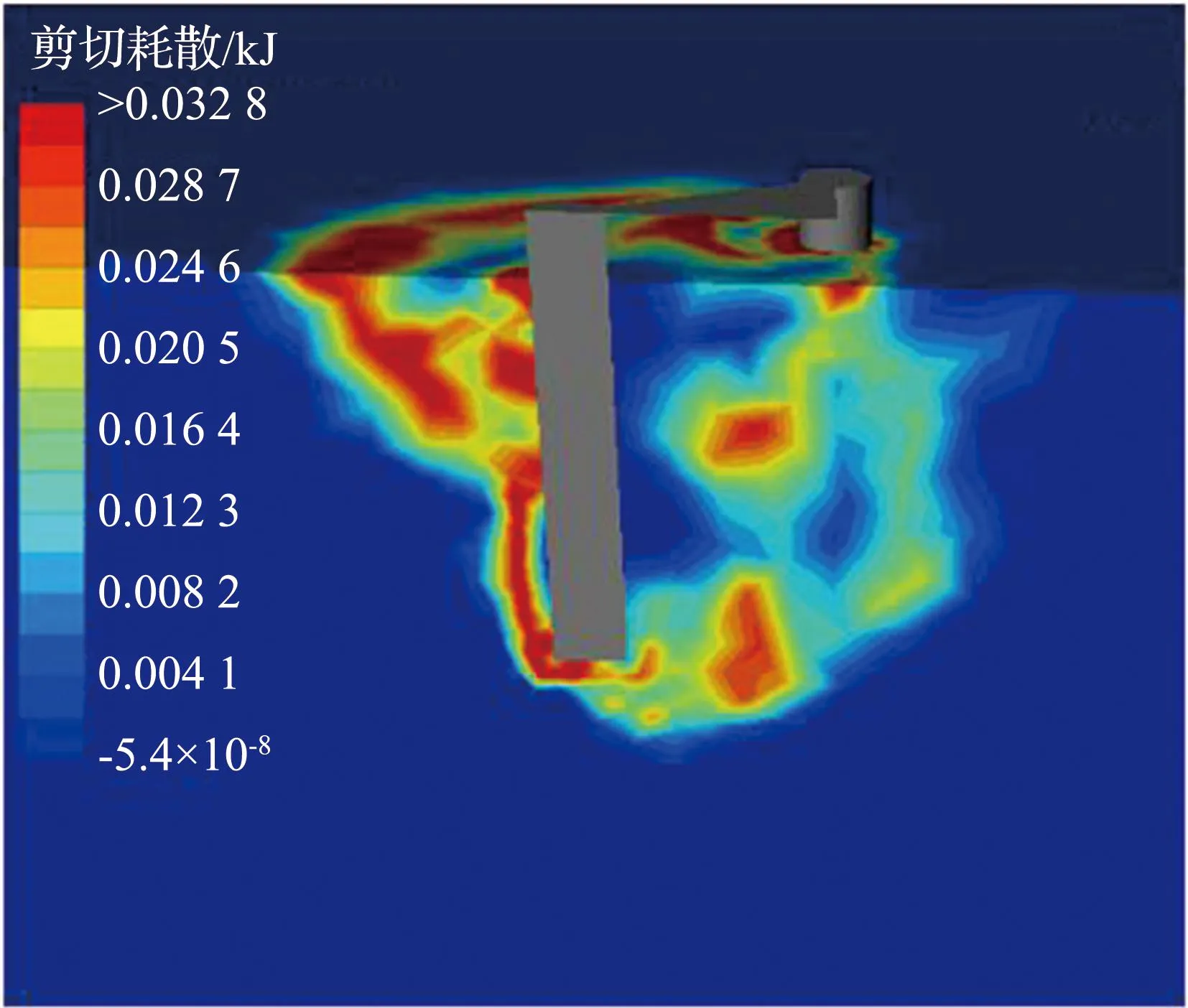
(a) P2以前
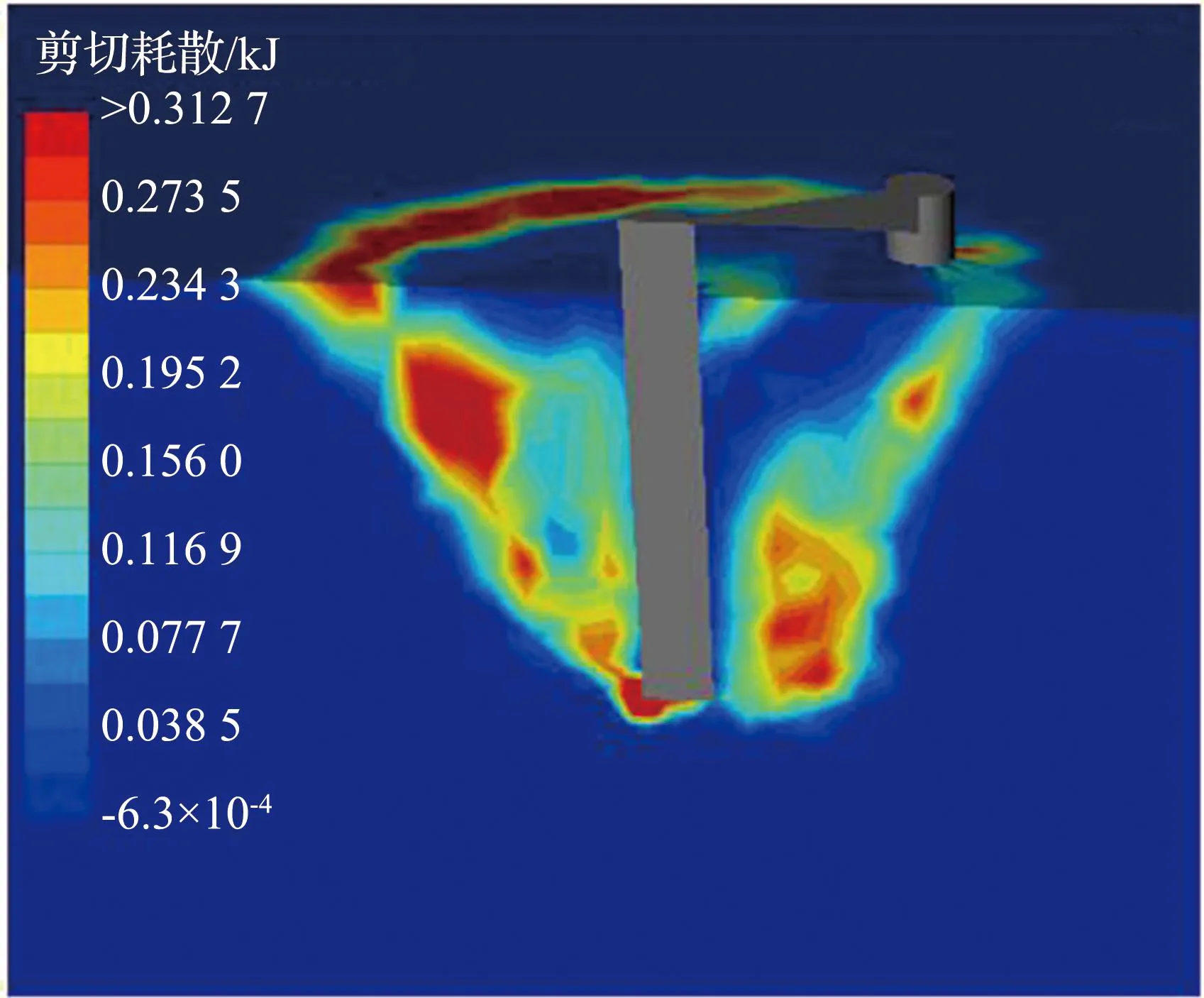
(b) P2以后图6 L/D=6和s/D=4时剪切耗散Fig.6 Shear dissipation patterns for L/D=6 and s/D=4
3.3 V-H-M空间中失效包络面
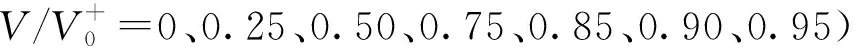
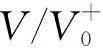
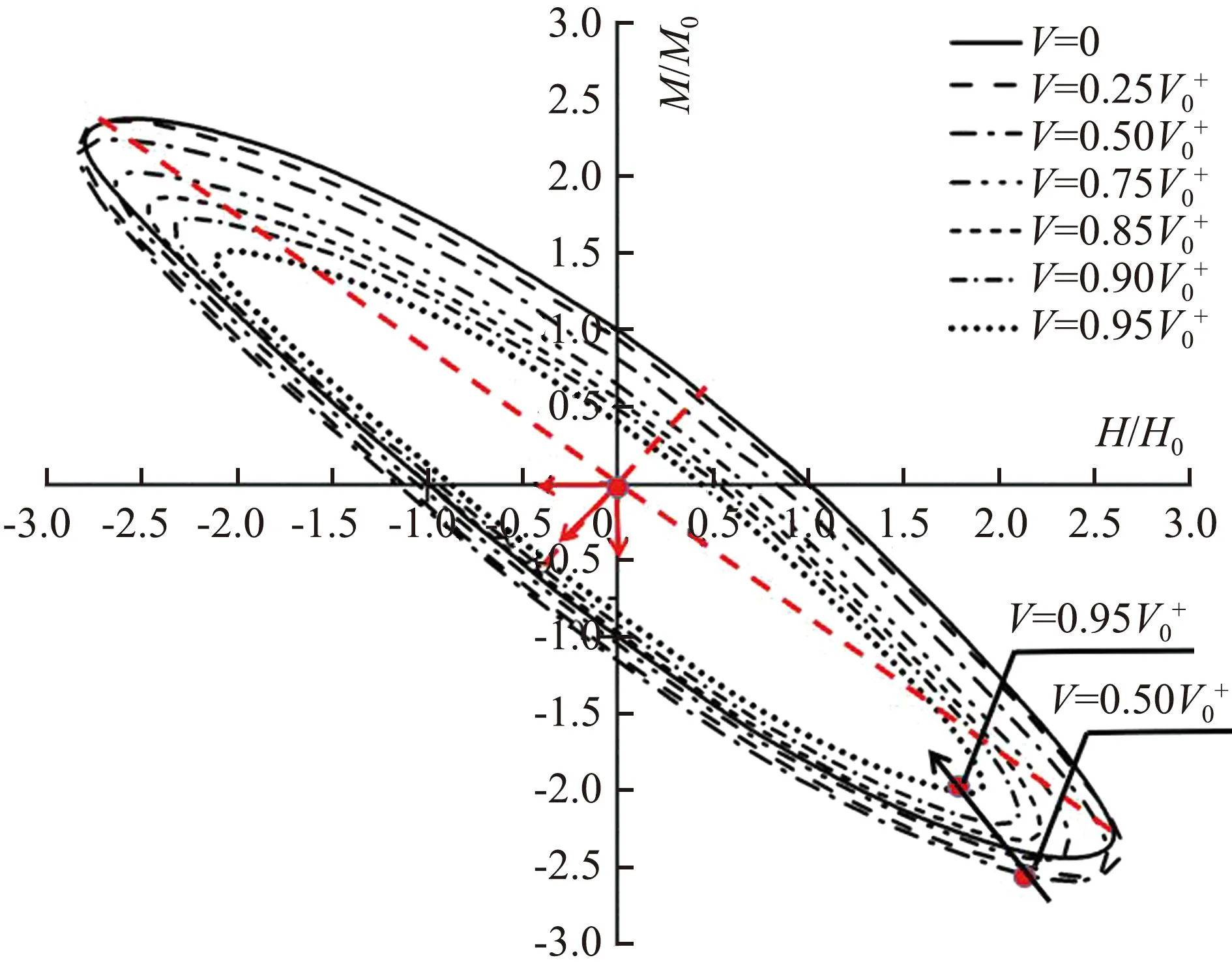
图7 L/D=6和s/D=4时竖向荷载对失效包络面的影响Fig.7 Effect of the vertical load on the failure surfaces for L/D=6 and s/D=4
除此之外,竖向荷载的大小也会影响三桩-土体系失效机制的变化。图8分别显示了当V/V0+=0.50和V/V0+=0.95时桩-土体系的失效机制。从图8中可以看出,在竖向荷载影响下桩-土体系的失效机制表现为倾覆-压入混合机制。当竖向荷载水平较低时(例如V/V0+=0.50),三桩基础主要受横向荷载影响发生侧向偏移,形成倾覆破坏,此时土体的剪切耗散多集中在靠近地表的浅层土体中[图8(a)];当竖向荷载较大时(例如V/V0+=0.95),基础主要受竖向荷载影响发生整体下沉,形成压入破坏,此时土体的剪切耗散面从桩底深层土体延伸至地面。
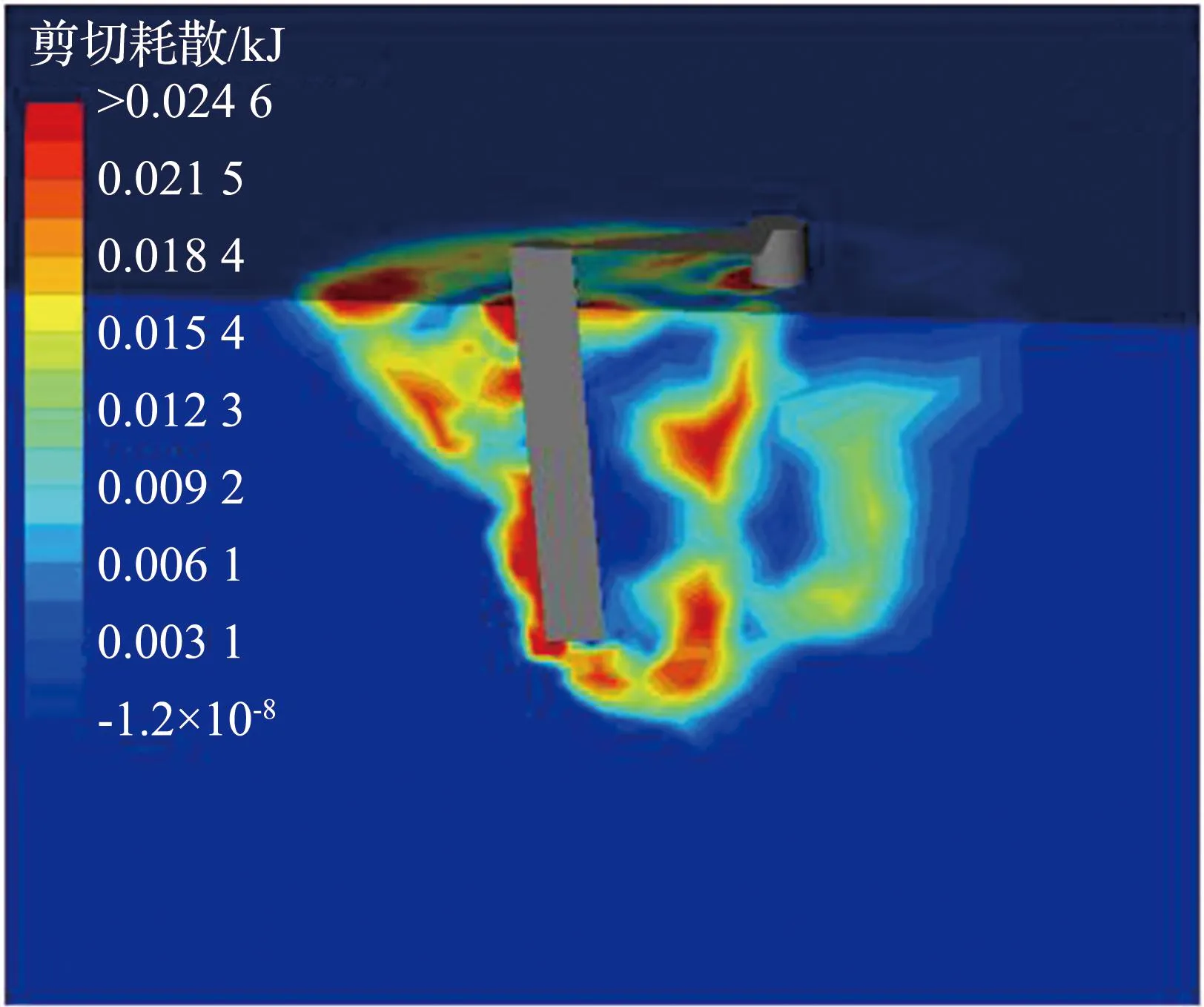
(a) V=0.50 V0+

(b) V=0.95V0+图8 桩-土体系的失效机制Fig.8 Failure mechanism for V=0.50V0+, V=0.95V0+
4 参数分析
4.1 深径比L/D
图9表示的是对应s/D=4的情况下,三桩基础深径比L/D对失效包络线的影响。图9(a)、(b)分别对荷载分量采用了无量纲化(H/suD2、M/suD3)和归一化(H/H0、M/M0)形式进行表示。由图9(a)可知,随着L/D的增大,三桩基础的复合承载力数值的增大十分明显,失效包络线上所对应的荷载分量最大值不断增加。同时对应最大值的固定加载比M/H绝对值也随着桩长的增加而增加。由图9(b)可知,当L/D增大时,三桩基础归一化承载力水平的增幅十分有限,失效包络线上所对应水平荷载分量的最大绝对值约为2.5。通过对其他距径比条件下的结果进行分析后得知,当距径比发生变化时,深径比L/D对失效包络线的影响规律也是类似的。
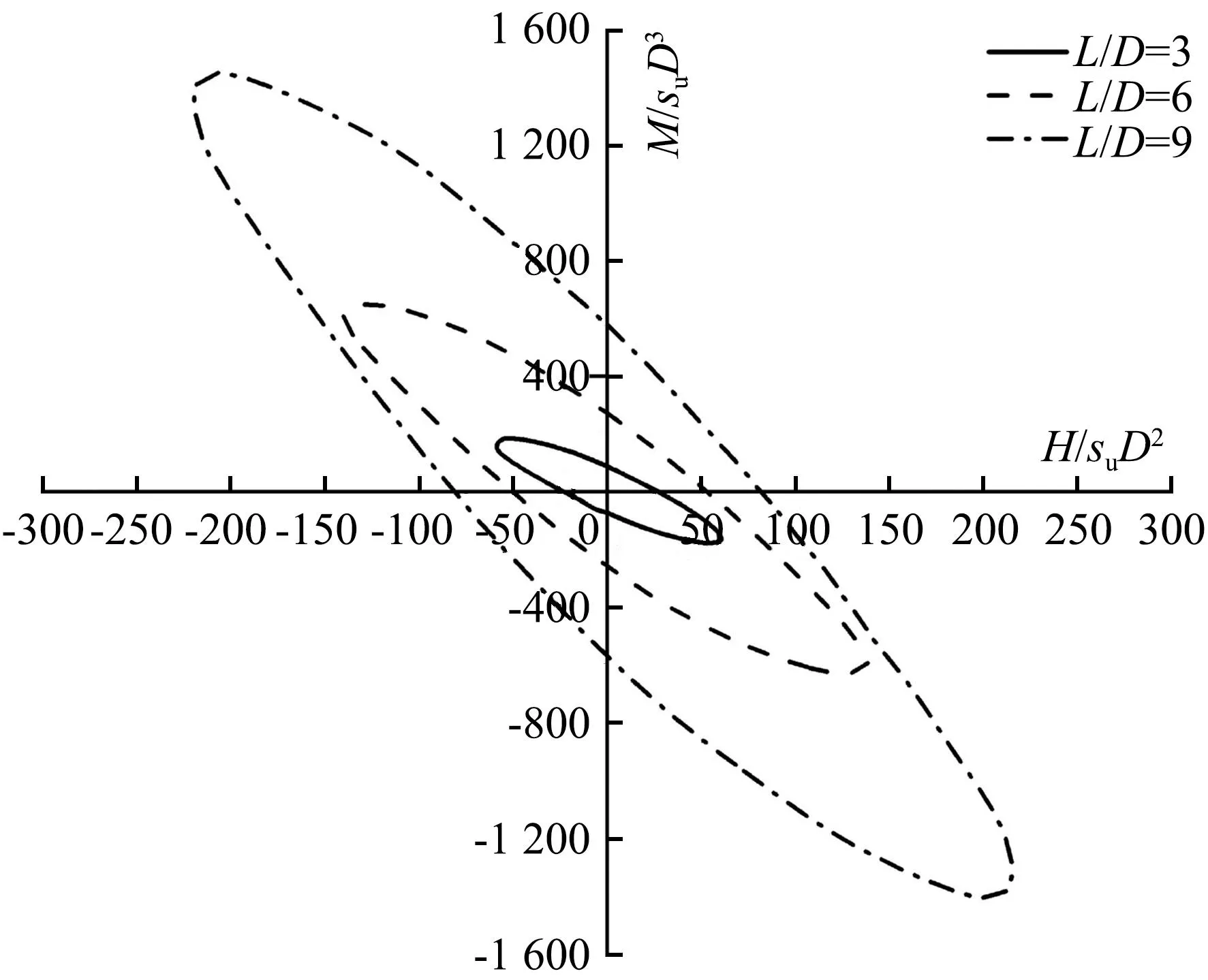
(a) H/suD2-M/suD3

(b) H/H0-M/M0图9 不同深径比下的失效包络线Fig.9 Failure envelope at different depth to diameter ratio
4.2 距径比s/D
图10表示的是对应L/D=6情况下,三桩基础距径比s/D对失效包络线的影响,图10(a)、(b)分别对荷载分量采用了无量纲化和归一化形式进行表示。由图10(a)可知,随着s/D的增加,三桩基础的复合承载力数值逐渐变大,失效包络线上所对应的荷载分量最大值也不断增加,但对应最大值的固定加载比M/H绝对值基本不变。由图10(b)可知,随距径比增加,归一化荷载(H/H0和M/M0)的最大绝对值反而会有所减小,说明相对于大间距情况,加载路径的改变使得小间距三桩基础复合承载力水平的显著增加。
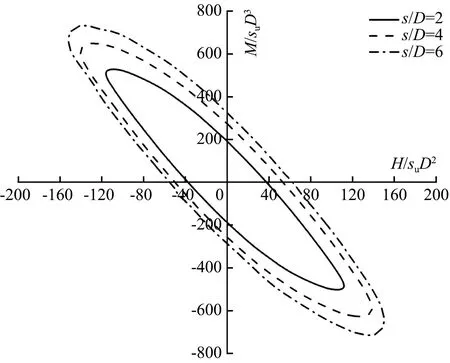
(a) H/suD2-M/suD3
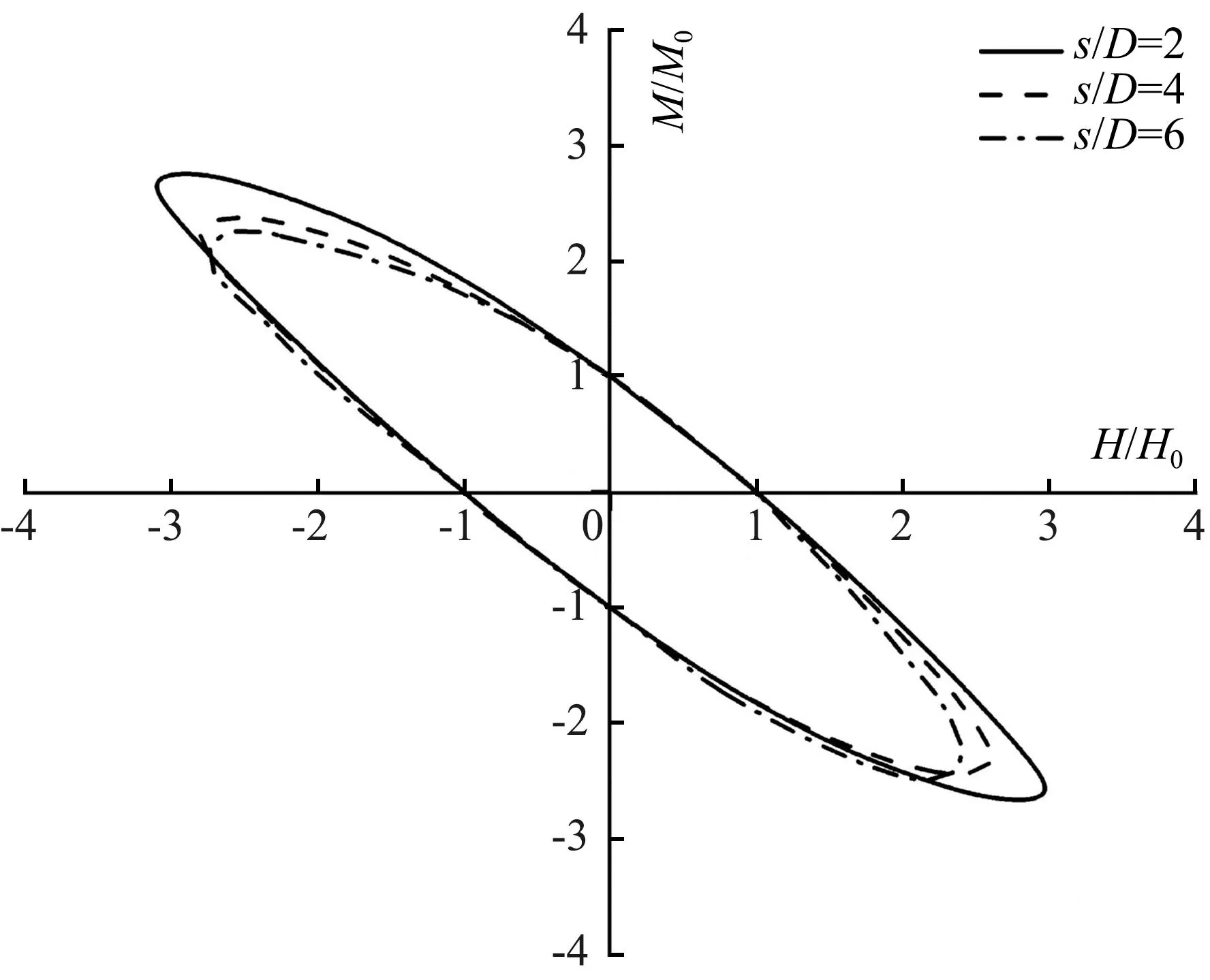
(b) H/H0-M/M0图10 不同距径比下的失效包络线Fig.10 Failure envelope at different pitch to diameter ratio
4.3 经验表达式
本研究根据H-M平面失效包络线位置与形状随竖向荷载的变化规律,采用超椭球体的特征表达式对三桩基础V/V0-H/H0-M/M0空间内的三维失效包络面进行拟合,具体公式为
(2)
(3)
(4)
(5)
(6)
(7)
经验公式中所有参数q、A、B、C的取值均考虑了不同的深径比L/D和距径比s/D情况。
图11展示了不同竖向荷载水平下(以V/V0=0与0.95为例),采用经验公式(2)对失效包络面的拟合效果。由图11可看出,在充分考虑三桩基础几何特征参数对失效包络面影响的前提下,通过经验公式中各参数的确定,式(2)可以较为准确地预测不同的深径比L/D和距径比s/D情况下三桩基础的失效包络面。
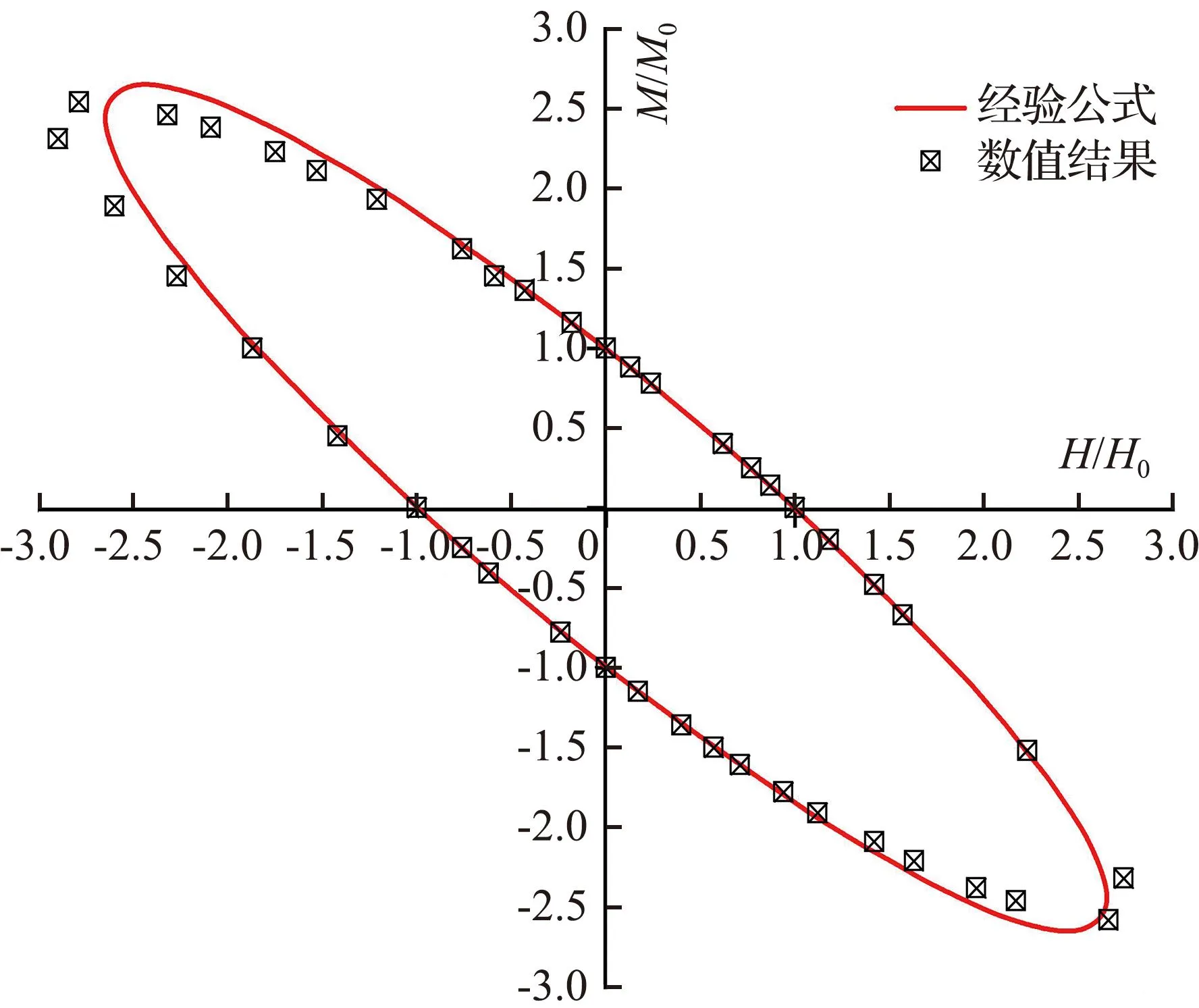
(a) L/D=3, s/D=2V=0
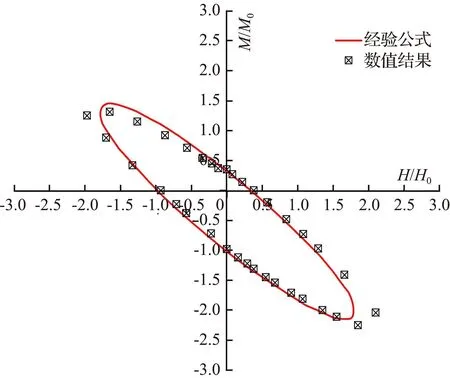
(b) L/D=3, s/D=2V=0.95V0
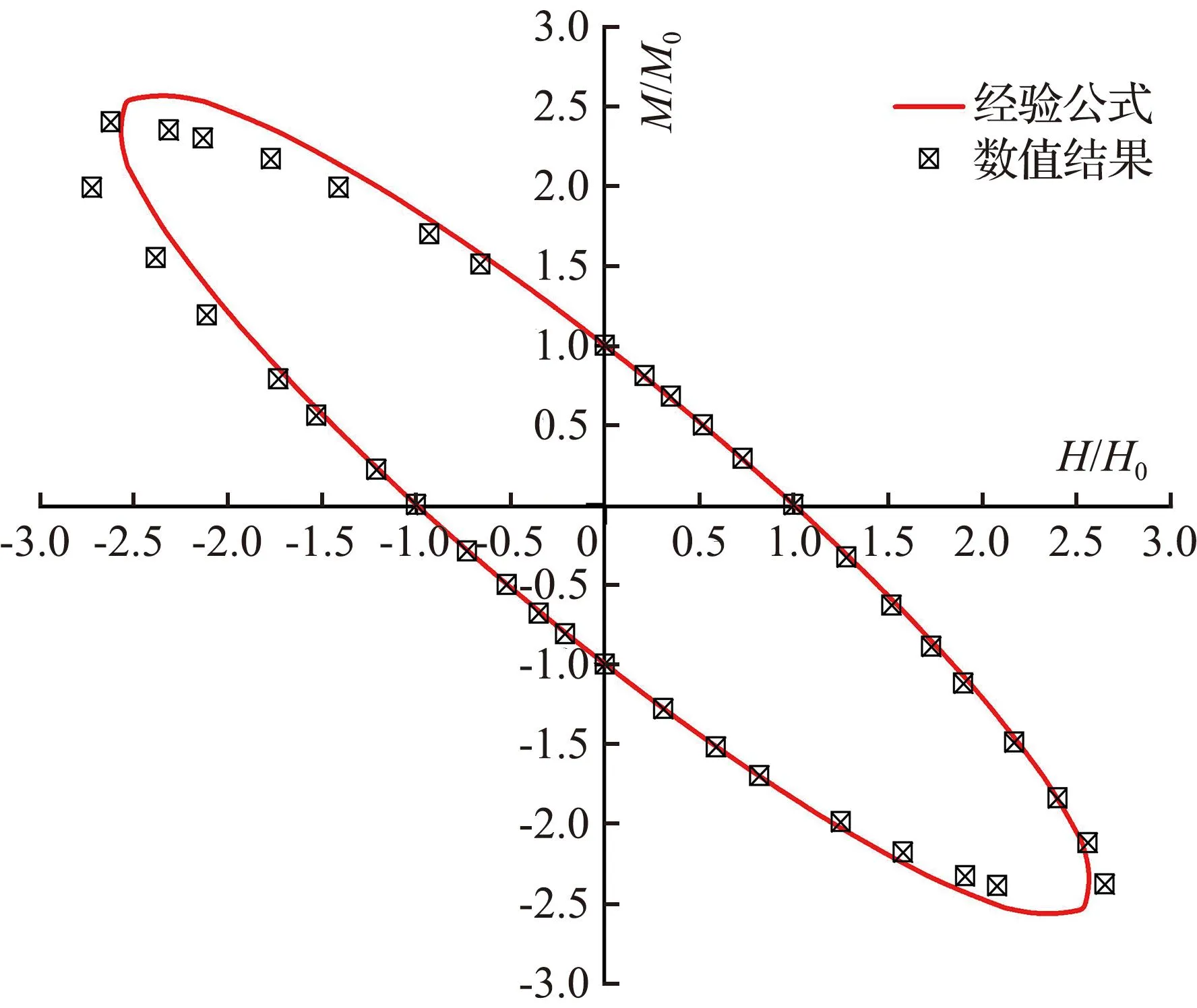
(c) L/D=6, s/D=4V=0
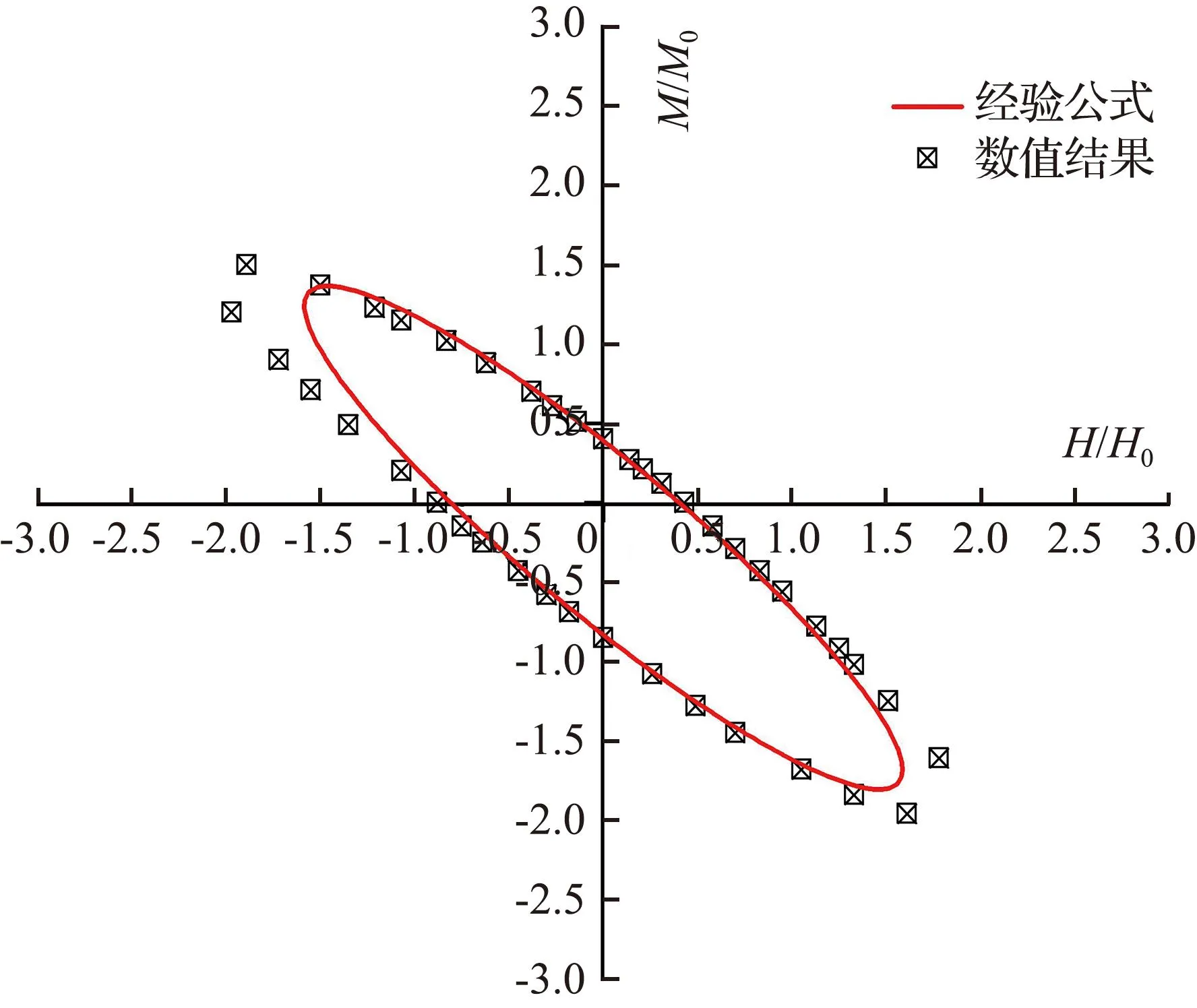
(d) L/D=6, s/D=4V=0.95V0图11 经验表达式提出的失效包络面与有限元极限分析结果的对比Fig.11 Comparison of the failure surfaces proposed by empirical equations with FELA result
5 结论
本文通过一系列数值分析对三桩基础在竖向荷载、水平荷载和弯矩荷载复合加载模式下的地基承载特性进行了研究,得到了基础在V-H-M三维空间内的失效包络面,得到的主要结论如下:
①H-M二维加载模式下三桩基础的失效包络线呈倾斜椭圆状,同时H、M的荷载分量最大值受加载方向的影响明显,P2′点的水平荷载极限值比P2极限值大约180 kN,基础的运动方向在最大值位置发生转变。

③ 深径比L/D和距径比s/D的变化对三桩基础H-M平面失效包络线的大小与形状会产生一定影响。当深径比L/D从3增长到9时,失效包络线发生明显扩大,同时其主轴顺时针转动,无量纲化水平荷载极限值从61.25增长到222.34。随着距径比s/D从2增加到6,失效包络线逐渐扩大,但其形状不发生变化,无量纲化水平荷载极限值从120.15增长到154.67。
④ 根据H-M平面失效包络线形状随竖向荷载水平及基础几何参数的变化规律,提出了描述三桩基础V-H-M空间内失效包络面的经验表达式,可用于评价复杂加载条件下三桩基础地基的承载力稳定性。
