一种用于辅助兵棋推演的快速决策框架研究

陈 健，赵建印，纪 红

(海军航空大学，山东 烟台 264001)

0 引言

现代兵棋是一种“两方或多方指挥员直接参与，依据一定数据、 规则，通过一系列对抗与裁决的过程，实现对行动过程模拟、逻辑研究、评估论证的工具”[1]。随着现代计算机技术与兵棋推演系统的融合发展，兵棋推演系统中的行为实体、行动过程、行为决策都会随着实际发展态势展现出不可预知的变化[2]。但是，现代兵棋推演系统在提高真实性的同时，也带来了另一个问题，即在推演过程中实施指挥决策的人员(指挥员)，不得不面对更复杂的实体构成和更不确定的推演环境，以及庞大的异构实体状态空间和行为空间。这使得在兵棋推演过程中，确定一个囊括己方所有实体的最优行动方案变得非常困难。加上信息技术的融合使用，模糊了传统兵棋回合制的概念，更快的推演节奏，要求双方指挥员在有限的时间内做出科学合理的决策部署。因此，构建一个相对通用、合理简化、反应迅速且具有较高准确性的快速决策框架，并基于该框架和具体的推演想定，实现推演的快速辅助决策系统，用来在复杂的推演环境中辅助指挥员优化各个阶段的行动策略，具有较高的现实意义。

1 研究现状及存在问题

目前，对兵棋推演中的辅助决策框架和决策系统有过很多研究。文献[3]将关注点聚焦在计算机兵棋博弈系统上，将知识规则与知识库作为核心，避免因为兵棋规则复杂而造成的决策困难，同时引入推理机构辅助知识推理，搭建了智能决策支持系统。文献[4]利用规则推理对具体类别的推演实体行为进行规划，将规划结果表示为行为树的节点，从而完成了实体行为树框架的搭建，实现动态决策。文献[5]提出了分层智能规划方法并搭建了完整模型。文献[6]同样使用行为树方法，研究了实体模型的外部自主决策过程。文献[7]在决策过程中引入了博弈的概念和机器学习中的决策树算法，建立了兵棋推演中的决策模型。上述研究存在两个共同的问题：一是决策模型(算法)大多较为复杂，适用于大型兵棋推演系统，但很难满足上文提出的合理简化和反应迅速的要求；二是大部分决策模型考虑的对象是计算机生成实体(CGF)或完全由计算机控制的智能体(Agent)，而不是兵棋推演过程中的指挥员。

2 快速决策框架设计

本文基于一般的决策和规划流程，提出了一个快速决策框架(Rapid Military Decision Framework，RMDF)，该框架针对异构实体模型和动态推演环境，基于一致性包算法实现任务分配，生成备选行动策略，通过简化的作用效果热图和概率模型实现行动策略的快速评估和决策辅助，能够在推演之前或推演期间，根据成功概率、生存能力提供行动方案的快速评估，可以有效地辅助兵棋推演指挥人员进行复杂态势下的兵棋推演。

本文提出的快速决策框架逻辑如图1所示。

图1 快速决策框架逻辑图

2.1 基于一致性包算法的任务分配策略

任务分配是制定行动方案的基础。任务分配指根据总的任务目标，将兵棋推演想定中的B方实体分配给A方实体(A、B互为对手)的过程，是一个典型的多实体任务分配问题。依据文献[8]提出的分类法，多实体协同任务分配问题等同于交叉调度的单任务多智能体时间 扩 展 任 务 分 配 问 题 (cross-schedule Dependent Single Task Multi-Robot Time-extended task Allocation，XDSTMRTA)，其中交叉调度是指想定中的实体是否执行某个任务受其他实体任务执行情况影响；单任务是指推演实体一次只能执行一个任务；时间扩展是指推演实体在执行任务之前需要预先进行任务规划。对于XDSTMRTA问题，常见的任务分配算法有集中式和分布式两类，相比集中式分配算法存在中央节点负荷大、系统鲁棒性差等缺点[9]，分布式算法可提供更好的稳健性以及负荷的均衡性，是目前广为采用的分配算法[10]。本文采用Choi等人提出的一致性包算法 (Consensus Based Bundle Algorithm，CBBA)作为推演实体任务分配算法。CBBA算法的特点是去中心化，同时可以很好地应用于异构实体模型和动态推演环境。文献[11]证明了CBBA算法可收敛到纳什均衡(Nash equilibrium)但非帕累托最优(Pareto optimal) 解，同时指出 CBBA算法可为单智能体单任务分配问题 (Single-Robot Single Task Task Allocation，SRSTTA)提供次优解决方案。当CBBA算法非负评分机制满足边际增益递减 (Diminishing Marginal Gain，DMG)的收敛特性时，CBBA算法相对于最优目标值可达到至少50%的最优性[12]，同时，由于CBBA算法运行时间为多项式时间，当推演实体和任务数量增多时，CBBA算法的可扩展性保证了其在实时动态环境下的适用性和快捷性[13]。

CBBA算法由任务包构建、冲突解决两个阶段构成，这两个阶段循环迭代直到完成任务分配，如图2所示。第一阶段采用基于市场的分布式拍卖策略作为任务选择机制，第二阶段使用基于局部通信的一致性策略作为冲突解决机制，结合分布式拍卖算法和一致性算法的优势，实现快速产生无冲突的可行解决方案。

图2 CBBA算法框图

2.1.1 任务构建

在RMDF框架中，推演实体采用贪婪的方式进行局部任务包的构建。每个推演实体绑定四个向量，分别是任务包bi，任务执行路径列表pi，获胜者列表zi以及获胜者出价列表yi。对于所有未分配的任务，推演实体将其连续添加到自身任务包中，并随着分配过程的进行不断更新上述四个向量，直到推演实体无法添加任务或任务全部分配完毕为止。

新任务添加到任务包中的方式为：计算各个推演实体执行各个任务的收益，从中选取收益最大的任务作为目标任务，相对应的推演实体作为目标实体。将目标任务的收益值与当前获胜者出价列表yi中对应的收益值进行对比，若目标任务的收益值更大，则将目标任务添加至目标实体的任务包中，并更新目标实体的四个向量。

(1)

边缘收益值是根据其添加到推演实体的任务包前后，推演实体的总收益值之差得到的。单个推演实体aj在tj时间完成任务j时的收益Jj(aj，tj)根据下式计算：

Jj(aj，tj)=e-λ·tjRj(aj)

(2)

其中λ为演实体aj的收益折扣因子。考虑到框架的便捷性，折扣因子可以根据推演实体的类型统一设置。

2.1.2 冲突解决

各推演实体完成自身任务包的构建后，进入CBBA算法的冲突解决阶段。在这个阶段中，推演实体通过局部通信共享各自的任务信息，实现任务冲突解决。相邻推演实体的共享向量包括：获胜者列表zi，获胜者出价列表yi以及新引入的时间戳集合si。

si表示推演实体i最后一次更新信息的时间，时间戳更新公式如下：

(3)

其中，τr是消息接收时间。

当同一任务出现在多个实体的任务包中时，收益值最高的实体竞拍到此任务，其余实体任务包的对应任务失效，同时获得目标任务的实体更新自身信息结构，即该推演实体会释放在目标任务之后添加的任务，并作为新任务由推演实体再次竞拍。

在本阶段，当实体i收到另一个实体k的zk、yk、sk时，实体i会根据自身zi和si来确定任务的最新信息。对任务i，实体i有三种可能的处理方式，决策规则如表1所示。

表1 推演实体冲突解决策规则表

2.2 评估决策

快速决策框架事实上是一个简化的推演评估系统原型。为提高框架的可扩展性和易修改性，本文采用了模块化的设计思想，根据决策流程特点和一般兵棋推演评估流程，将框架分为四个子模块，分别是：引擎模块、环境模块、实体模型模块和视图模块。

(1)引擎模块：引擎模块的核心作用是实现推演评估的驱动，包含推演流程控制、任务分配、路径控制、基础策略等将模拟过程向前推进的关键方法。其中任务分配使用上文介绍的CBBA算法。

(2)环境模块：环境模块包含一个经过简化的推演环境对象，为了支持快速决策，框架将复杂的推演环境简化为空中、地面、海上三个不同的环境层，每一层以环境网格的方式表示，同时在网格内附加任务、地形、敌方实体等信息。

(3)实体模型模块：实体模型模块包含有关兵棋推演期间使用的推演实体和任务的必要信息。为了创建异构的推演实体，框架支持包括地面实体(UGV)、水面实体(USV)、空中实体(UAV)和防空实体(CAD)等多种异构推演实体。

(4)视图模块负责以快速推演过程的可视化表示。

快速决策框架的总体框架如图3所示。

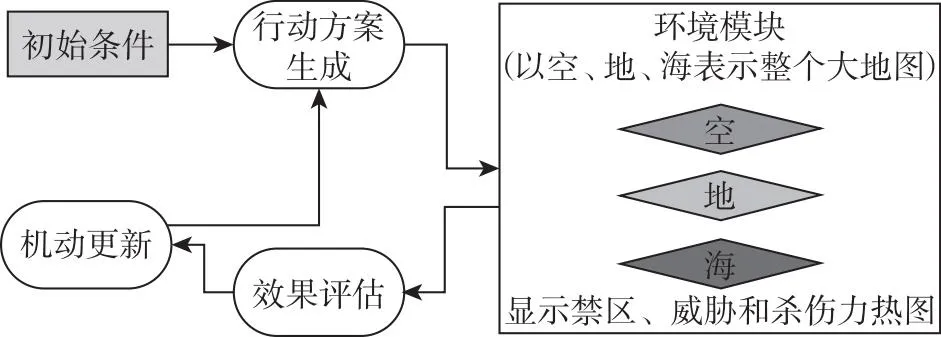
图3 快速决策模型总体框架

2.2.1 折扣因子与实体配置

实体配置是推演决策过程中的重要环节，推演实体配置与CBBA算法的收益函数密切相关，如上文所述，CBBA算法的收益函数如下：

Jj(aj，tj)=e-λ·tjRj(aj)

(4)

其中给出了推演实体aj在tj时间完成任务j时的收益。收益由两部分构成，第一部分是任务的标准收益Rj(aj)，该收益是一个与推演实体索引aj相关的函数；第二部分是折扣收益，它是任务j完成时间t的函数，考虑到在实际情况中，完成给定任务的收益与完成任务的时间具有负相关性，为了更贴近实际，在目标收益中引入了折扣因子-λ·tj，用于表示目标收益随时间递减的特性。

由于折扣因子是任务完成时间t的函数，因此，在设定折扣因子时，需要考虑推演想定中行动范围(地图)的大小，并据此设定合适的折扣因子或折扣因子取值区间。当折扣因子的区间确定后，可以通过CBBA算法来优化不同阶段的推演实体配置，提出了如图4所示的优化结构，从而基于折扣因子获得优化后的推演实体配置。

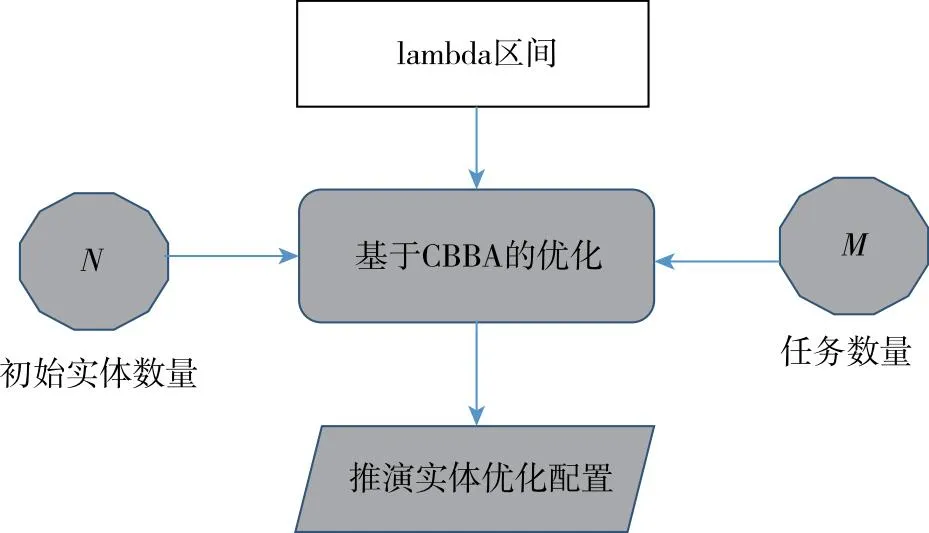
图4 基于折扣因子的实体配置优化

2.2.2 环境层与杀伤率

在模拟环境中，框架基于核密度估计(KDE)算法，通过估计地图上给定点相对于对手实体位置的危险级别(即对手实体单位的有效性级别)，将指定区域内对手实体的作用要素。在本文提出的快速决策框架中，假定推演实体的作用效果分布与其作用距离相关，采用Epanechnikov函数作为核函数。

(5)

(6)

其中d是推演实体与地图上指定点之间的距离。d=0时，推演实体的杀伤率取分布的最大值1。

首先，在地面层，空中实体、地面实体、水面实体和防空实体都可以在特定的作用区域对A方构成有效威胁。第二，在海上环境层，水面实体是主要威胁，但空中实体、地面实体和防空实体也作为有效的敌方实体加以考虑。第三，在空中环境层，A方的威胁主要来自于B方的空中实体和防空实体，如果在该区域存在B方的防空力量，则在该区域的作用效果上，将体现出对A方的重大威胁。

2.2.3 简化的行动模型与行动评估

行动建模抽象并简化了实体的行为和相互关系，本文提出的框架基于概率对行动模型进行简化，以健康度Hp、作用效果L、命中概率PH、探测概率PD、瞄准系统可靠性PT、设备可靠性PW和层效能系数EL作为HL系统F的影响因子。

F=Hp·L·PH·PD·PT·PW·EL

(7)

除此之外，推演实体的损伤效果建模对行动模型也非常重要，框架通过损伤矩阵定义推演实体在交战中对抗对手的有效性。在模拟环境中，框架采用如表2所示的作用矩阵。

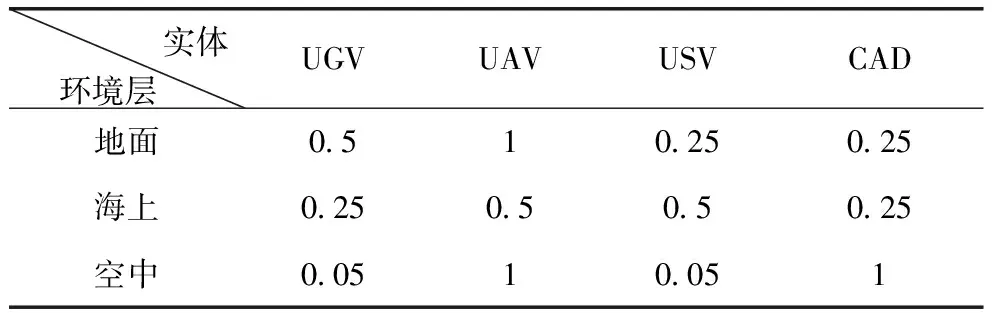
表2 不同环境层的推演实体作用系数

推演实体的能力按照下列公式给出的方式进行简化建模。

Fk=Fk-1-Fok

(8)

Mk=Mk-1-Mok

(9)

其中，Fk、Mk分别是k时刻推演实体的HL和机动性。Fok是时间k时对手实体的HL。

框架以双方推演实体的平均机动性和平均HL能力作为行动评估指标，平均机动性和平均HL能力的计算公式如下所示。

(10)

(11)

其中x表示A方和B方，t表示资产对应的环境层，F、M是推演实体交战后的机动性和HL能力，n是对抗后的幸存的推演实体数量。

3 仿真验证

为了验证本文所提出的快速决策框架的可行性和准确性，在试验环境中构建一个简单的推演系统对框架进行仿真。

在验证框架所使用的推演想定中，双方的实体是异构的，可用推演实体包括了无人飞行器、地面车辆和水面船只。无人飞行器建模时考虑了其中高空长航程能力；地面车辆基于通用运输车的性能进行建模，同时假设该地面车辆具有在任何地形下移动的能力；水面船只基于小型无人船的特点建模。由于推演实体的载油量和油耗特点对于任务的分配至关重要，因此这些参数在建模时予以特别考虑。异构实体模型的参数如表3所示。

表3 推演实体建模的核心参数

推演环境设定为一个小型的100×100的网格环境，推演任务是A方需要穿越B方防守区域，并竟可能多地消灭B方实体。初始的A方推演实体为2架无人飞行器，B方的推演实体为不同网格环境中的不同位置的1辆地面车辆以及2架无人飞行器。推演结果如表4所示。

表4 第一次推演结果

从表4数据中，可以看到即使选择了适宜的折扣因子λ，A方仍然没有能够完成任务。由于B方的空中实体仍然幸存，因此A方对推演实体的配置进行更新，针对B方空中存在幸存实体，增加A方的空中力量，即在相同的想定下，A方无人飞行器由2架增加到3架。B方实体部署不变。推演结果如表5所示。

表5 第一次推演结果

可以看出，在同样的场景中，A方通过调整决策，即调整A方的实体配置，确保了任务的完成。

4 结论

本文提出了一种面向兵棋推演的快速决策框架，来加速推演过程中的行动方案分析和决策优化。通过分层的网格环境来简化表示复杂的推演环境，通过推演实体的核心参数来确定其性能模型和行为模型。敌方实体的作用效果，简化为地面、海上和空中三个网格环境层次上的作用效果。通过一致性包算法实现推演实体的自动任务分配，通过快速仿真实现推演策略的优化。仿真表明，该框架具有较高的可行性和执行效率。

在确保效率的前提下，对一致性包算法进行改进，使其适应多实体联合任务分配是下一步的研究内容。在确保准确性的前提下，通过引入更多的随机分布，如增加实体间通信的不确定性、态势感知的不确定性来更好的模拟现实，也是下一步的重点研究内容。