依赖差分隐私：关联数据集下的高斯机制*

欧阳恒，陈洪超

(贵州轻工职业技术学院 信息工程系，贵州 贵阳 550025)

0 引言

在真实世界许多数据集中，数据集元组之间存在相互依赖关系，而非独立。Kifer和Machanavajjhala[5]发现，当数据元组有依赖关系时，DP存在一定的局限性。Zhu等人[6]提出关联元组的非交互式直方图发布方法，首次解决了元组间相关性带来的隐私泄露风险。Liu等人[7]提出ε-依赖性差异隐私(ε-DDP)，并使用拉普拉斯机制实现噪声扰动。Zhao等人[8]优化了Liu等人提出的拉普拉斯机制，添加更少的噪声来解决元组间的相关性引起的隐私泄露。然而，基于依赖差分隐私的高斯机制的研究还存在一定的空白。

本文主要贡献：一是提出了一种推理攻击，对手利用元组之间的依赖性从差分隐私查询结果中获取敏感信息，二是本文提出(ε，δ)-依赖差分隐私((ε，δ)-DDP)的定义，量化了二范数敏感度，并设计了一种高斯机制实现(ε，δ)-DDP的噪声扰动。

1 相关概念

定义1(相邻数据集[9])假设数据集D和D′具有完全相同的数据属性结构，如果数据集D和D′之间至多只相差一条记录，即|D-D′|=1。数据集D和D′是相邻数据集(Adjacent Datasets)。

定义2((ε，δ)-差分隐私，(ε，δ)-DP[10])设一个随机机制M：R→Y，满足(ε，δ)-差分隐私，则对于任意两个邻近的数据集D和D′，M(D)所有的输出E⊂T，有下列不等式成立：

P(D)∈E]≤eεP(D′)∈E]+δ

(1)

其中隐私预算ε是隐私保护程度的一个参数，平衡数据的安全性和可用性。δ(通常很小)是能够容忍不满足ε-差分隐私的部分，如果δ=0，那么满足ε-差分隐私。ε-差分隐私一般称为纯差分隐私，(ε，δ)-差分隐私一般称为近似差分隐私

定义3(全局敏感度[11])数据集D和D′至多相差一条数据，对于任意一个查询函数f：D→Rd，函数f的全局敏感度为：

(2)

定义4(隐私损失函数[12])设一个随机机制M，隐私损失函数LM，D，D′(Y)可以表示为M作用到相邻数据集D和D′，输出随机变量Y相同时两个概率之间的距离。定义如下：

(3)

其中FM(D)(Y)是输出随机变量Y=(D)的概率密度函数，如果选择高斯机制添加噪声，那么隐私损失函数同样服从高斯分布，即LM，D，D′(Y)=(Δ2f/2σ2，Δ2f/σ2)[13]。

2 差分隐私的隐私风险

由于在真实的应用领域中，数据集中的元组其实有着相互依赖的关系[14]，而差分隐私在提出之初就隐含着构成数据集的数据元组之间是相互独立的假设。事实上，这是一个薄弱的假设，尤其是因为由于用户之间的社会关系、行为习惯和基因相互作用[15-16]，导致元组依赖在数据集中必然存在。例如，在社交网络图中(节点代表用户，边代表“友谊”关系)，图中未明确连接的两个节点之间的“友谊”可以从其他节点之间存在的边推断出来[17]。对手可以访问扰动后的查询结果，并且知道用户的直系亲属是被查询数据库的一部分，因此很容易推断出用户对传染病的易感性。对手可以使用辅助信息通道访问这些依赖关系，并利用差分隐私中的缺陷，获取隐私数据，如图1所示。

图1 元组依赖的图例

一个数据集D=(Di，Dj)，其中Di和Dj具有概率依赖关系，设Dj=0.5Di+0.5X，考虑一个简单的推理攻击，其中一个对手发出一个和查询：f(D)=Di+Dj，此时对手可以推断出Di的值。

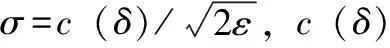
P[M(Di=1，Dj)∈E]/P[M(Di=0，Dj)∈E]≤eε

(4)

其中c(δ)≥1，不等式(4)恒成立。

P[M(Di=1，Dj)∈E]/P[M(Di=0，Dj)∈E]≤eε

(5)

式(5)将在1≤c(δ)≤1.5范围内不成立，存在隐私泄露的风险。

3 (ε，δ)-依赖差分隐私

传统的差分隐私，作用于元组相关的数据集时，并不能有效得防止上述攻击，存在隐私泄露得风险。

定义5(依赖相邻数据集[7])若数据集D(L，R)中一个元组值的变化，导致数据集D′(L，R)中最多有L-1其他元组的值产生变化，引起的变化大小关系为R，则数据集D(L，R)和D′(L，R)是依赖相邻数据集。

定义6((ε，δ)-依赖差分隐私，(ε，δ)-DDP)设一个随机机制M：→满足(ε，δ)-DDP，则对于任意两个依赖邻近数据集D(L，R)和D′(L，R)，M(d)所有的输出E⊂有下列不等式成立：

P[M(D(L，R))∈E]≤eεP[M(D′(L，R))∈E]+δ

(6)

其中L表示依赖大小，R表示数据元组之间依赖关系的大小。

3.1 DDP全局敏感度

(7)

其中，由于Di从di1到di2的变化，输出结果是有界的。

使用高斯噪声扰动查询结果。首先将式(7)进一步变换为下列等式：

(8)

等式(8)的右边第一项进一步计算，可以得到：

(9)

其中ΔDi是由于Di的变化而产生的最大差异。从等式(9)可以看出，与传统的差分隐私的噪声方差完全相同，因此(ε，δ)-DP只是在Di和Dj不相关时的一个特例。而式(8)的右边第二项包含Di和Dj的依赖关系，也就是相关性。

(10)

其中ρij表示Di的变化将引起Dj发生变化的依赖程度。最后，结合式(8)～(10)，可以得到：

(11)

(1)因为ρij是衡量两个元组的相关性的大小，因此ρij∈[0，1]。

(2)当ρij=0时，此时元组间没有相关关系，满足(ε，δ)-DP。

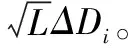
(4)是不对称的，即ρij≠ρji(例如：遗传病父母可以影响子女，而子女却不能影响父母)。

前面分析了两个元组依赖关系下，敏感度的度量，类似的可以推广到包含两个以上元组的数据集上的任意查询函数的场景。

定理1(依赖敏感度) 数据集D(L，R)和D′(L，R)是依赖相邻数据集，对于任意一个查询函数f：D→Rd，函数f的依赖敏感度为：

(12)

其中，j∈[1，2，…，L]表示有L个元组与第i个元组的相关程度，且ρij=1。

3.2 (ε，δ)-DDP高斯机制算法

根据依赖敏感度，本文设计了一个有效的高斯机制来实现(ε，δ)-DDP和支持依赖元组上的差分隐私扰动，并描述了基于现有高斯机制的依赖差分隐私高斯机制算法，该算法满足(ε，δ)-DDP。

定理2((ε，δ)-GMA-DDP)对于依赖数据集D(L，R)上的一个查询函数f：D→Rd，其依赖敏感度为Δ2fDS，随机机制M满足(ε，δ)-DDP，则需要满足下式：

M(D)=f(D)+(0，σ2)

(13)

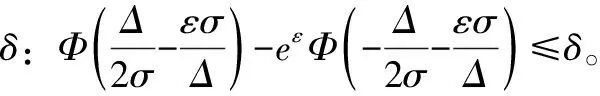
根据以上的噪声扰动机制，可以顺利对一个查询返回含有噪声的结果，并且满足(ε，δ)-DDP的隐私保证，然而在交互式查询中，通常需要回答多次查询，这种情况下，是否依然满足相应的隐私保证。因此，对于(ε，δ)-DP的组合定理，在(ε，δ)-DDP中同样适用。

3.3 (ε，δ)-DDP安全分析

本文采用Kifer等人[5]提出的两个隐私公理：变换不变性和凸性性质，分析(ε，δ)-DDP的安全性。任何完整的隐私定义都应该满足这两个公理。

定理3(变换不变性)对于任意一个随机算法M作用在依赖大小为L和依赖关系为R的数据集D(L，R)上，且M满足(ε，δ)-DDP，那么对于其他任何随机化算法A，Am(·)=A(M(·))也满足数据集D(L，R)上的(ε，δ)=DDP。

证明：P[A(M(D))=E|di1]

=∑DP[A(O)=E]P[M(D)=O|di1]

≤∑DP[A(O)=E]eεP[M(D)=O|di2]+δ

=eεP[A(M(D))=E|di2]+δ

定理4(凸性性质)对于任意两个随机化算法M1、M2作用在依赖大小为L和依赖关系为R的数据集D(L，R)上，且都满足(ε，δ)=DDP，设Mp表示一个算法，该算法以概率p运行M1，以概率1-p运行M2，那么Mp也满足数据集D(L，R)上的(ε，δ)=DDP。

证明：

P[Mp(D)=E|di1]

=pP[M1(D)=E|di1]+(1-p)P[M2(D)=E|di1]

≤eεpP[M1(D)=E|di2]+eε(1-p)P[M2(D)=E|di2]+δ

=eεP[Mp(D)=E|di2]+δ

4 实验结果

4.1 实验环境与数据集

该实验中所使用的软硬件具体参数如下：

(1)操作系统：Windows10；

(2)硬件参数：Intel(R)Core(TM)i7-10700F CPU，2.9 GHz，RAM内存16 GB；

(3)编译环境及工具：Python3.6，PyCharm。

本文采用Adult真实数据集IPUMS。从2022年的1 700条数据，选取了其中10 000条数据，其中每条数据包括以下4个属性：Total personal income，Total family income，Age，Sex。

4.2 实验结果分析

实验前将采用的数据集元组间的依赖程度设置为固定值：0.5。与Liu等人[7]在2016年提出的线性算法(Baseline)和依赖差分隐私的拉普拉斯机制(DDP-Lap)对比，设置查询为“平均个人总收入”，因为在上述数据集中，用户的个人总收入在0到100 000之间，所以敏感度为(100 000-0)/10 000=10。0<εi<1中随机采样，δ=0.1。

如图2所示，随着查询次数的增加，查询结果中的噪声之和逐渐累积，Baseline算法绝对误差与查询次数呈线性关系，这将使得添加的噪声非常大，导致查询结果不可用，正如预期的那样，GMA-DDP的噪声量明显低于Baseline算法与DDP-Lap，这表明GMA-DDP向查询结果中添加了更少的噪声，使查询结果更接近于真实结果，并达到了相同的隐私保护水平。

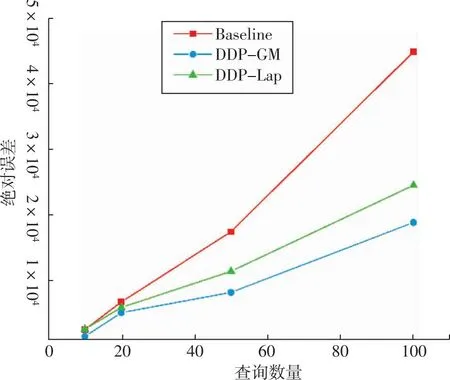
图2 GMA-DDP误差对比

如图3所示，本文也从(α，β)=Accuracy的角度来对比三个算法的隐私性与可用性的平衡，这是衡量隐私性与可用性的常用指标。实验表明，GMA-DDP在相同的隐私水平下具有更高的可用性，在相同的可用性下，降低隐私预算的开销，提供更强的隐私保护水平，尤其在隐私预算较小(高隐私水平)的情况下，GMA-DDP的可用性更高。

图3 GMA-DDP效用对比

5 结论

本文针对差分隐私定义应用到依赖数据集时，存在隐私泄露风险的问题，根据(ε，δ)=DDP的定义，量化了在依赖数据集下敏感度的大小。根据依赖敏感度，设计了满足(ε，δ)=DDP的噪声扰动机制—依赖高斯机制。最后在真实数据集上，将GMA-DDP的可用性与Baseline算法和DDP-Lap进行对比，实验结果表明GMA-DDP有较好的可用性。