负载口独立控制系统非线性滤波振动抑制方法
2024-04-10程敏侯严迪丁孺琦
程敏,侯严迪,丁孺琦
(1. 重庆大学高端装备机械传动全国重点实验室,400044,重庆;2. 华东交通大学载运工具与装备教育部重点实验室,330013,南昌)
由于具有高功率质量比、高负荷能力等优点,液压传动技术已在建筑工程、军事、农业、航空航天等领域得到广泛应用[1-2]。在传统电液比例方向阀控制系统中,采用单阀芯比例阀来控制液压执行器的进出油口,油口的负载口面积由阀体内的阀芯位移进行耦合调节,易于操作且鲁棒性强[3]。然而,单阀芯机械耦合会在负载口处产生不必要的损失,造成大约30%的能量消耗,导致能源利用率较低[4]。此外,单阀芯比例阀应对超负荷负载的灵活性较差,操作性能与节能性能难以同时达到最佳效果[5-6]。
负载口独立控制系统分别使用两个比例阀控制进油口与出油口,打破了进出口之间的机液耦合,从而得到广泛的研究与应用[7-8]。此控制系统不仅增加了控制自由度,可实现多种控制策略,还能降低系统的能耗[9]。在负载口独立控制系统中,可按照控制需求分别给定进出口阀信号,使执行器按照期望速度运行,并可通过增大出口阀开度,将背腔压力维持在一个较低水平[10]。然而,这样做的同时会降低系统阻尼,从而引起执行器速度振荡现象,导致系统出现平稳性差、机械设备寿命减少等问题[11-13]。此外,对于挖掘机、起重机等大多数工程机械,均是通过给定手柄信号控制执行器速度,但手柄信号的突变会导致液压缸两腔压力急剧变化,也会引起液压系统中的速度振荡,由于这种信号突变的存在范围涵盖了多种机械设备、工况环境以及操作对象,因此具有一定的广泛性和普遍性[14]。这时,需要采取措施避免信号突变造成的液压系统中的压力冲击[15],以降低系统的速度波动。
在液压控制系统中,通常利用阻尼补偿方法来提高系统阻尼,减少突变信号下的速度振荡。研究人员提出了多种利用反馈信号检测系统振荡并进行反馈的方法,如执行器负载力[16]、加速度[17]及两腔压力等[17-18]。Alexander等[13]提出了基于加速度反馈与压力反馈的主动阻尼减振方法,并定量比较了两种方法对系统阻尼的影响。Pedersen等[19]提出了压力直接、低通滤波、压力梯度及高通滤波4种压力反馈方法,指出不同的应用场景可能需要不同的反馈方案。Cheng等[20]利用加速度反馈与压力反馈的主动阻尼补偿方式抑制振荡,并比较了两种方法的阻尼补偿效果。Ding等[21]通过极-零点位置分析了由反馈增益和截止频率组成的控制参数的动态响应,并采用动态压力反馈与主动阻尼控制相结合的复合控制方法,对负载口独立控制系统的阻尼进行优化。
虽然上述阻尼补偿方法对抑制系统振荡具有一定效果,但根据文献[21]的研究结果,反馈增益过大或过小均会引起执行器更加剧烈的速度振荡。此外,合理选取反馈增益难度大且耗时长。与此同时,阻尼补偿方法也无法减小液压缸活塞惯性力在负载口信号突然变化时引起的速度振荡。因此,在负载口独立控制系统中,如何降低突变信号引起的速度振荡,是当前亟需解决的核心问题。
针对上述问题,本文基于负载口独立压力流量复合控制系统,首先分析了引发速度振荡与压力波动的原因;其次,提出了利用非线性滤波器修改手柄突变信号的控制方法,并给出了非线性滤波器边界选取原则;然后,设计了负载口独立系统的进出口阀控制器;最后,以挖掘机作为仿真对象,分析了不同控制方法和工况下挖掘机执行器的运动特性,验证了所提方法的有效性。
1 压力流量复合控制
在负载口独立控制系统中,常常使用两个比例方向阀控制液压缸的进出油腔,并通过手柄给定信号分别对执行器的速度与压力进行控制,使执行器的速度与背腔压力维持在一个定值。系统运行过程中,通常会给定进出口阀信号,使执行器按照期望速度运行,但突变的速度信号会引起系统压力冲击,从而产生执行器速度振荡现象。此外,由于挖掘机等工程机械的工作条件复杂,执行器速度需根据不同的工作要求频繁改变,且工作期间载荷波动较大,严重影响了系统运行的稳定性与操作舒适性[22-24]。因此,为提升液压系统的运行稳定性,研究给定速度信号下系统的稳态特性,探究影响其运行稳定性的因素,优化液压系统的控制信号并提升其工作稳定性,具有十分重要的意义。
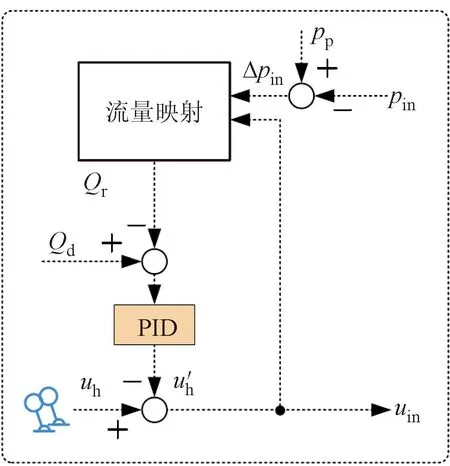
在负载口独立控制系统中:Qr为进油腔实际流量信号,Qd为进油腔期望流量信号,pin为进油腔的实际压力,pp为泵的出口压力,Δpin=pp-pin为进口阀的前后压差,uh为原进口比例阀信号,u′h为进口阀PID反馈信号,uin为进口阀的控制信号,po为实际背腔压力,pr为出口阀的阀后压力,pod为背腔期望压力,Δpo=po-pod为实际背腔压力与背腔期望压力的差值,uf为原出口阀控制信号,u′f为出口阀PID反馈信号,uo为出口阀的控制信号,up为泵的控制信号,Qin为进口阀的阀后流量,Qo为出口阀的阀后流量,A为液压缸无杆腔,B为液压缸有杆腔,mt为液压缸的等效负载质量。基于压力流量复合控制方法,阻抗伸出模式下负载口独立控制系统的液压原理图如图1所示。
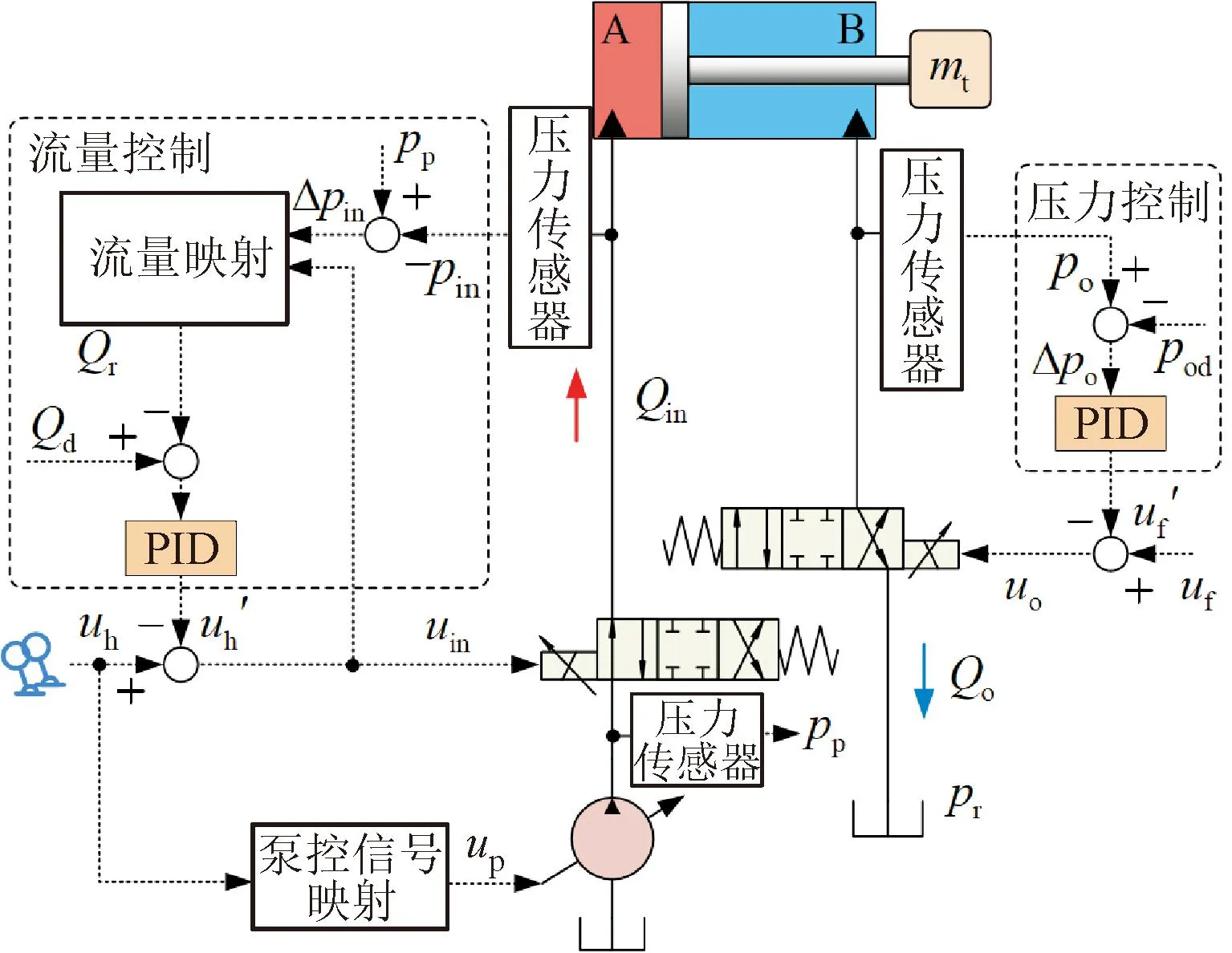
图1 负载口独立控制系统原理图Fig.1 Schematic diagram of independent metering control system
由于阀芯位移与负载口节流面积之间的非线性关系,以及各参数值在工作过程中都会随着工作点的变化而变化,从而导致流量控制精度低且影响系统的动态稳定性。因此,本文根据进口阀两端的压差给定比例阀的电压信号值,并结合标定好的比例阀压力流量特性曲线,实时在线计算通过进口阀的实际流量,再与期望的流量值进行比较,最后通过比例积分微分(PID)控制器调整负载口开度以减小实际流量与期望流量之间的误差。此控制系统的进口阀采用电子压力补偿的流量控制方式,可认为执行器的稳态速度不受负载变化的影响,出口阀采用电子压力补偿的压力控制方式。
采用压力流量复合控制的负载口独立控制系统具有多个阀芯的输入值,输出值为执行器速度和执行器压力,因而系统为双输入、输出系统。但由于液压系统中的速度与压力之间存在一定的耦合关系,因此会使两者之间互相影响,进而影响控制性能,引发系统振荡[9]。
2 非线性滤波控制器设计
上述分析表明,突变的速度信号会引发系统压力冲击,与此同时,液压系统的速度与压力耦合关系会影响系统控制的稳定性,进而造成执行器的速度波动与压力振荡。抑制系统振荡最直接的方法是引入加速度反馈感知振荡程度,并以此来动态调整负载口开度,从而提高阻尼特性并保证系统能效。然而,在实际作业工况中,由于成本较高或不方便安装等问题,位移、速度、加速度等传感器难以适用于挖掘机等工程机械的强冲击负载工况,且系统压力可能受到多种因素的干扰,包括液压系统的泄漏、摩擦和温度变化等,因此需要采取补偿措施确保控制的精度和稳定性。与传统阻尼补偿抑振方法相比,非线性滤波器无需额外传感器,降低了系统开发成本,且计算速度较快,能够在较短时间内对信号进行处理从而实现快速响应。在负载口独立控制系统中,快速响应性能够减少系统振荡时间,从而提高系统的动态性能。此外,利用非线性滤波器可避免参数整定的复杂流程,易于实现模块化编程。根据设定的机械臂关节力矩和速度边界,Gerelli等使用非线性滤波器在实现轨迹规划的同时降低了系统速度突变[25]。本文提出了采用非线性滤波器修改负载口独立控制系统的突变控制信号,以实现动态调整负载口控制信号,从而降低系统振荡。此外,所提出的非线性滤波抑振方法也可以适用于文献[26]中的工况对象,以解决负载口独立控制系统存在的普遍问题。
系统整体由控制信号、控制器以及控制对象组成,其总体控制框图如图2所示。由压力传感器采集进油腔的压力信号,采用流量控制使执行器的速度不受负载变化的影响,通过非线性滤波器减少突变信号引发的速度振荡;由压力传感器采集出油腔的压力信号,采用压力控制使背腔压力维持稳定。最终生成进口阀与出口阀的控制信号,控制执行器动作。
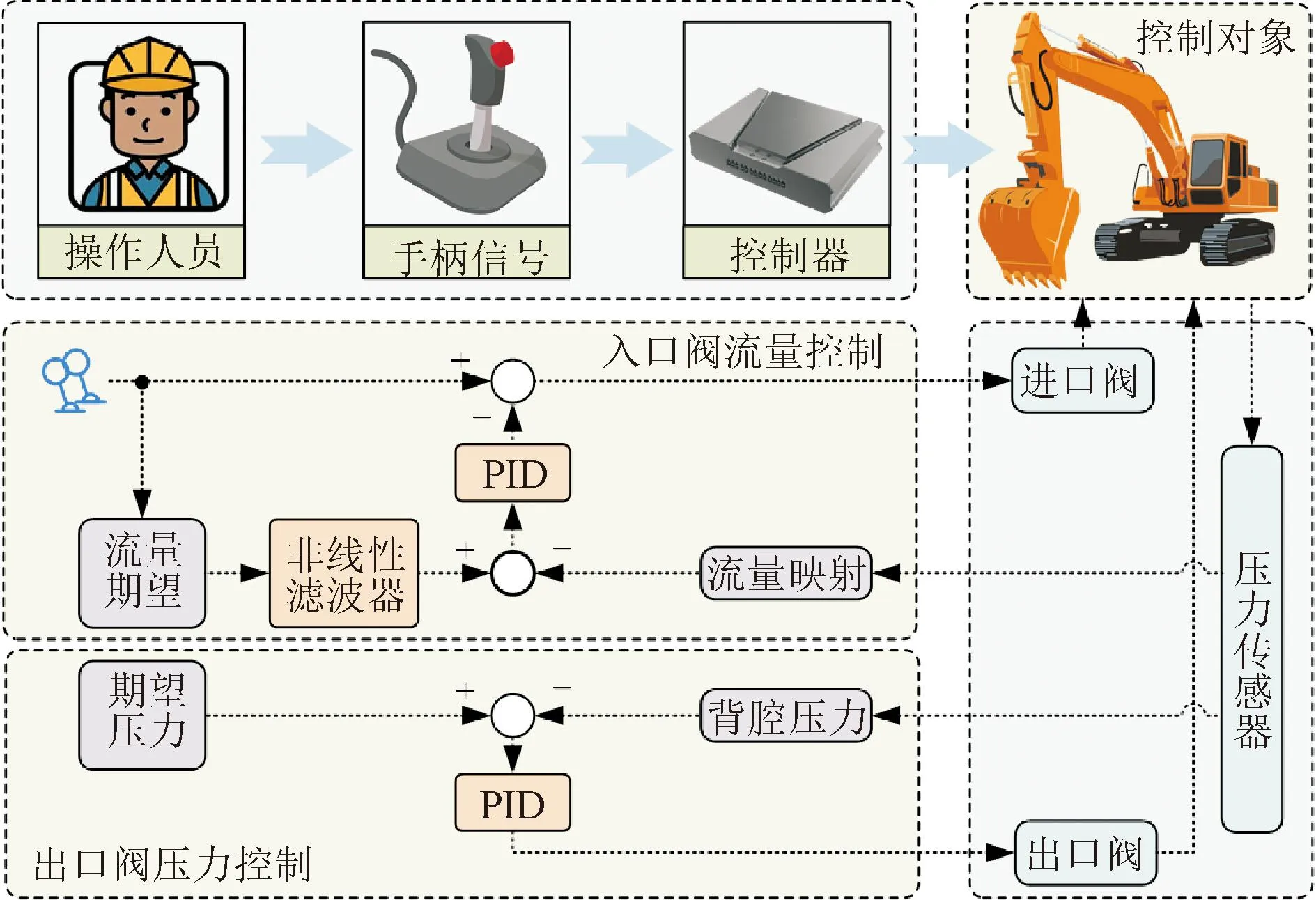
图2 具有非线性滤波器的负载口独立控制系统框图Fig.2 General block diagram of independent metering control system with nonlinear filters
2.1 基于流量的非线性滤波器
为降低突变的速度信号对系统振荡的影响,提出了利用非线性滤波器[25]修改参考流量信号的控制方法。根据参考流量信号及其一阶导数,结合设计流量信号的一、二阶导数边界,通过控制器得到修改后的流量信号。
定义参数y为修改后的流量信号与参考信号之差,表示如下
y=Qm-Qd
(1)
(2)
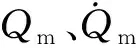
(3)
(4)
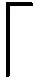
(5)
(6)
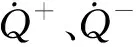
通过上述定义,可得到不同情况下输入信号的二阶导数边界值α、β,表示为
(7)
(8)
定义计算步数中间变量γ的表达式
(9)


(10)
(11)

(12)
(13)
(14)
(15)
式中:μ为系统状态与滑膜面之间的差值;u为非线性滤波器输出的控制信号;sat(μ)为饱和函数。
结合上述推导方法,可得到非线性滤波器的控制原理框图,如图3所示。
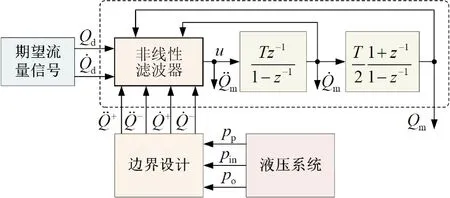
图3 非线性滤波器控制原理框图Fig.3 Block diagram of nonlinear filter control
根据式(14),可得到修改后流量信号的二阶导数,对其进行两次积分,即得到修改后的流量信号,表示为
(16)
式中:下标t表示第t个采样时刻。
2.2 流量导数边界设计
为了得到各执行器流量的一阶导数边界,需要计算关节加速度边界,通过映射关系得到流量信号的一阶导数向量。不考虑摩擦力和末端的接触力,机械臂的动力学方程可写为
(17)
R=diag[r1,r2, ,rk, ,rn]
(18)
式中:rk为液压缸相对于关节的力臂,可将液压缸输出力映射为关节扭矩,下标k表示第k个关节(k=1, 2, ,n)。
执行器结构图如图4所示。其中:lj为关节j到活塞杆末端的距离,下标j表示第j个连杆 (j=1, 2, ,m),且k=j,m=n;lj1为关节k到基座的距离;lj2为活塞杆位移为零时液压缸两端铰点的距离;活塞位移xp∈ [0,lj2];θk为基座和关节k连线与水平方向的夹角;qk为机械臂关节角;mc为末端负载质量。
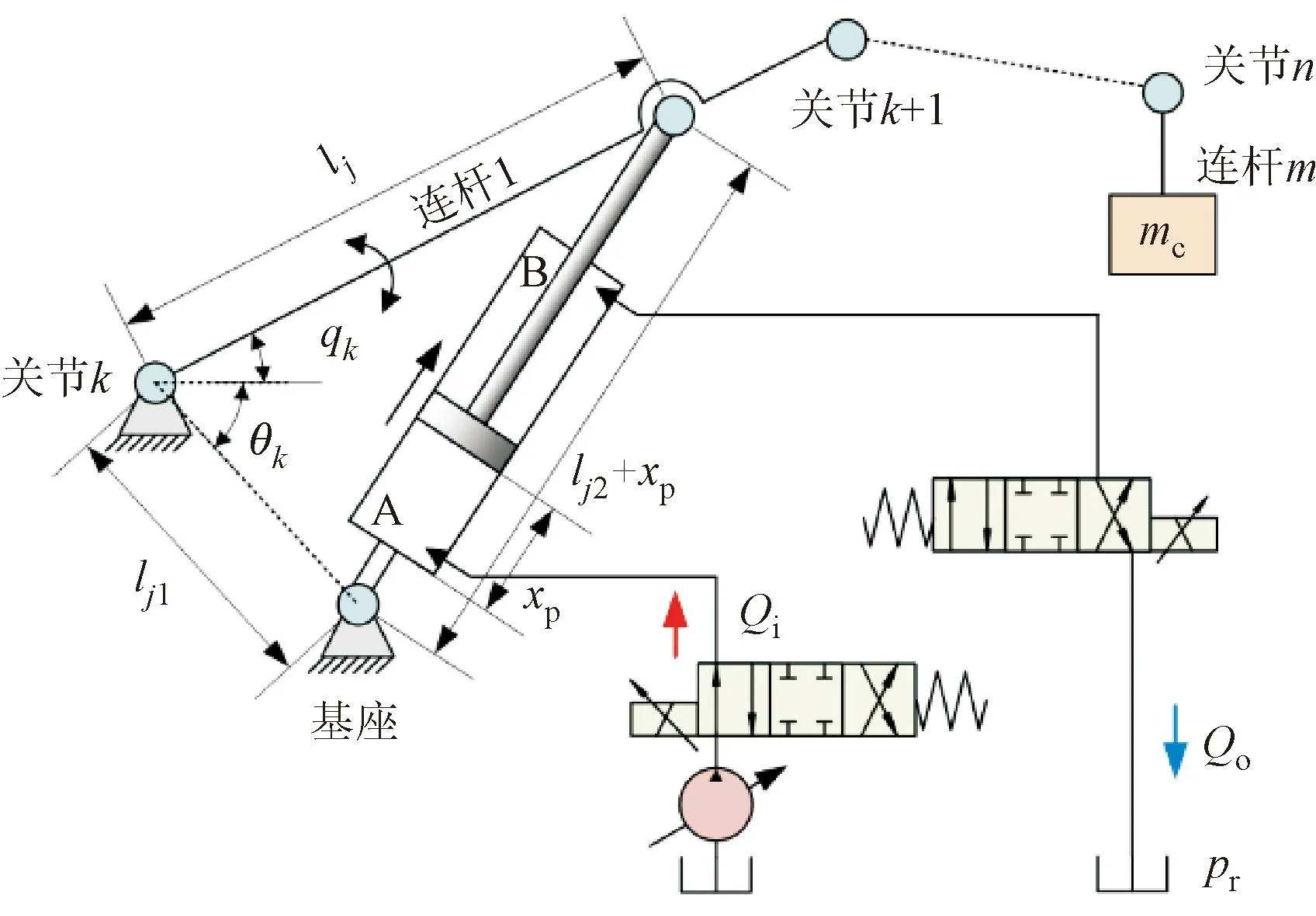
图4 执行器结构图Fig.4 Actuator structure diagram
由图4,机械臂关节角q与液压缸活塞位移xp的关系可表示为
(19)
(20)
根据式(19),液压缸速度与关节角速度的关系可写为
(21)
(22)
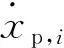
F=[F1,F2, ,Fi, ,FN]T
(23)
Fi=pin,iSin,i-po,iSo,i
(24)
式中:Fi为根据两腔压力计算得到的第i个液压缸的驱动力;pin,i、po,i分别为第i个液压缸的无杆腔和有杆腔压力;Sin,i、So,i分别为第i个液压缸的无杆腔和有杆腔面积。
根据式(17),关节角加速度的下边界与上边界可定义为
(25)
(26)
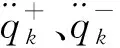
根据式(23),设计液压缸的最大、最小驱动力矢量分别为
Fmax,i=[F1,F2, ,Fmax,i, ,FN]T
(27)
Fmin,i=[F1,F2, ,Fmin,i, ,FN]T
(28)
式中:Fmax,i、Fmin,i为第i个液压缸的最大和最小输出力,可分别表示为
Fmax,i=
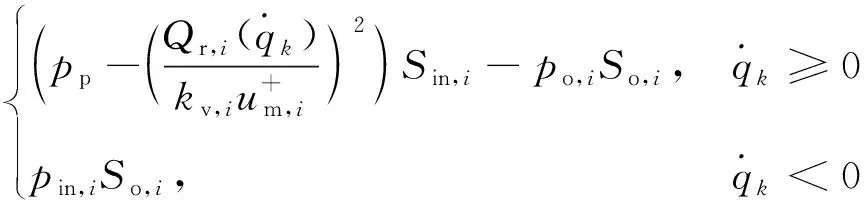
(29)
Fmin,i=
(30)
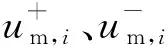
根据求得的关节加速度边界,通过映射关系可得液压缸的加速度边界,表示为
(31)
(32)

最后,根据液压缸加速度边界,可求得流量信号的一阶导数边界向量,表示为
(33)
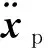
流量的二阶导数边界可定义为
(34)
(35)
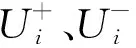
通过所设计的非线性滤波器边界选取原则,能够限制流量信号的一阶导数边界及二阶导数边界,修改期望流量信号,进而降低控制信号突变的影响,从而减小系统的速度振荡。
3 进出口阀控制器设计
3.1 进口阀控制
液压系统进口阀采用电子压力补偿的流量控制方式,从而使执行器的速度不受负载变化影响,通过计算流量反馈的方法控制执行器的速度,可使比例阀动态流量对应的压差增益与其稳态增益不一致,能够在获得流量控制高精度的同时提高系统的稳定性。
加入PID控制后的进口比例阀控制信号uin可表示为
uin=uh+u′h
(36)
式中:u′h为进口阀PID反馈信号,可写为
(37)
式中:Kp为比例系数;Ki为积分系数;Kd为微分系数;ΔQ=Qm-Qr,Qm为经过非线性滤波器的期望流量信号,Qr为实际流量信号,可表示如下
(38)
式中:kv为流量系数。
此外,为实现节能目的,本文中的电比例变量泵采用开环排量控制方式。首先,根据手柄信号及负载信号前馈,计算执行器所需要的流量;然后,通过泵的流量特性及原动机的转速,计算泵的控制信号。同时考虑到变量泵存在内泄漏,需要进行相应的补偿,其控制信号up可写为
(39)
式中:Qv,i为第i个液压缸所需流量;Ck为变量泵的泄漏系数;kp为变量泵的排量增益;np为变量泵的转速。
3.2 出口阀控制
执行器出油腔采用压力控制方式,通过PID控制出口阀,将出油腔(背腔)压力维持在一个较低水平,以提高系统能量利用效率。出口阀控制信号uo可表示为
uo=uf+u′f
(40)
引入PID控制器,根据实际压力与期望压力的差值来实时调整出口阀开度,则出口阀信号反馈控制项u′f可写为
(41)
式中:Δpo=pod-po,即实际背腔压力与背腔期望压力的差值。
系统运行过程中,可根据修改后的进口阀流量信号Qm实时控制出口阀。当Qm为0时,出口阀关闭,此时式(40)可表示为
(42)
由此,结合上述非线性滤波器控制方法,得到系统的控制原理图如图5所示。
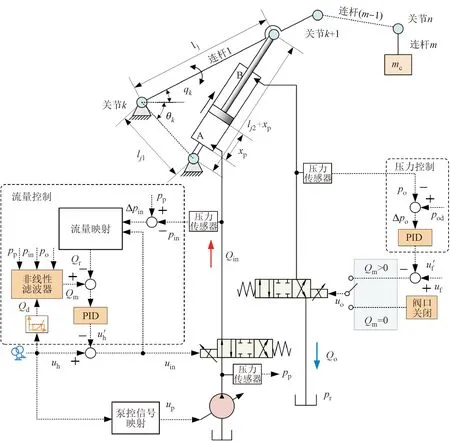
图5 非线性滤波器控制原理图Fig.5 Schematic of nonlinear filter control
4 仿真验证
为验证所提方法的有效性,在考虑比例方向阀动态特性、油缸黏性摩擦及泄漏的基础上,基于MATLAB/Smiulink平台搭建20 t挖掘机机电液仿真模型,并根据第2节中非线性滤波器边界的选取原则,得到不同工况下流量信号的一阶导数边界及二阶导数边界,并对非线性滤波器的抑振效果进行测试。挖掘机的模型参数如表1所示。与斗杆相比,动臂的载荷变化范围更大且等效负载质量更高,导致阻尼性能较差,且执行器速度波动更加剧烈。因此选择动臂液压缸作为控制对象,并以阻抗伸出模式为例进行仿真,与无抑振控制方法及传统阻尼补偿控制方法进行比较,通过对比执行器速度、进油腔压力、进口阀信号的仿真数据,验证本文所提出的非线性滤波抑振方法的控制效果。记无抑振控制方法为C1,传统阻尼补偿控制方法为C2,本文提出的非线性滤波抑振方法为C3,3种控制方法的控制原理框图分别如图6所示,3种方法的详细描述如下。
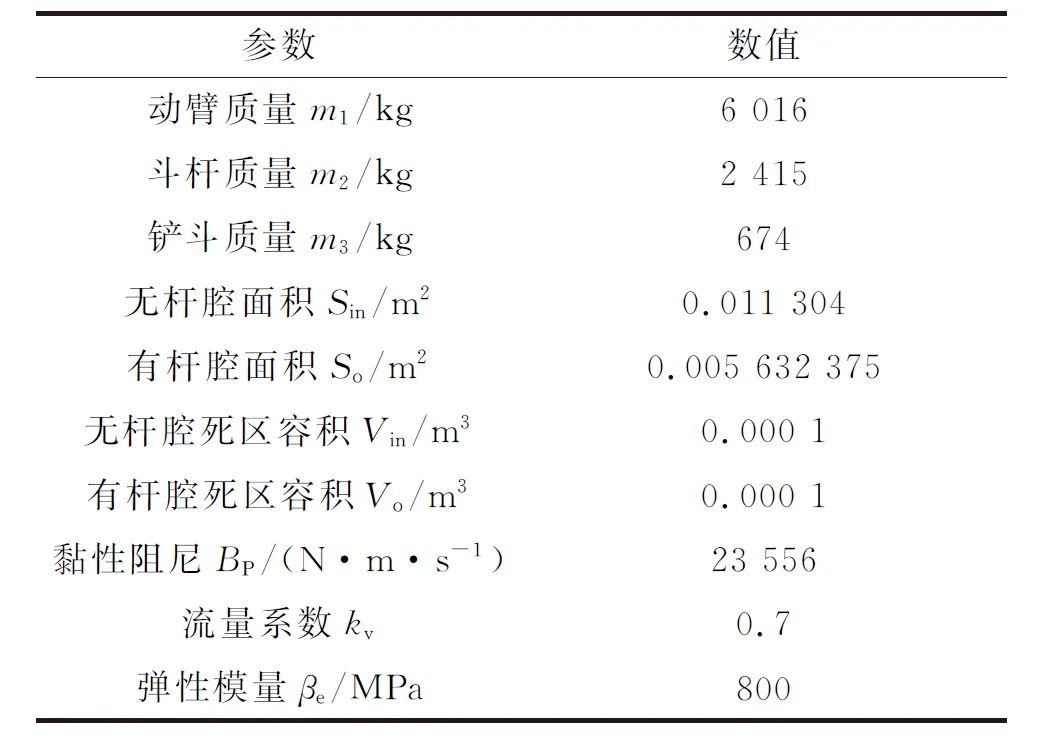
表1 挖掘机模型参数Table 1 Excavator model parameters
(a)方法C1
(1)方法C1:进口阀采用电子压力补偿的流量控制方式。
(2)方法C2:进口阀采用电子压力补偿的流量控制加阻尼补偿控制方式。
(3)方法C3:进口阀采用电子压力补偿的流量控制方式,在原进口比例阀信号后增加非线性滤波器。
此时,3种控制方法的负载口独立控制系统的出口阀均采用电子压力补偿的压力控制方式。由于所采用的研究方法具有普适性,所以该抑振方法同样适用于其他执行器。
工作中,20 t挖掘机的最大承载能力为1 116 kg,通过挖掘机实际参数,可计算出挖掘机的等效负载质量[11]。本文结合挖掘机在实际工作中的速度范围,设计了4种与实际作业条件相符的工况,以充分验证所提出控制方法的有效性。其中,工况1为斗杆液压缸全伸且动臂期望速度为0.02 m/s,此时铲斗为空载状态;工况2为斗杆液压缸全伸且动臂期望速度为0.06 m/s,此时铲斗为空载状态;工况3为斗杆液压缸全缩且动臂期望速度为0.02 m/s,此时铲斗负载为1 116 kg;工况4为斗杆液压缸全缩且动臂期望速度为0.06 m/s,此时铲斗负载为1 116 kg。
阶跃信号时,采集4种工况下执行器速度、进油腔压力及进口阀信号的仿真数据,如图7所示。

(a)工况1
由图7可见,与无非线性滤波器和阻尼补偿方法相比,在高速/低速条件下,采用增加非线性滤波器的控制方法,可使执行器的速度振荡与压力波动均明显降低。为更加直观地体现增加非线性滤波器的控制效果,定义速度振荡降低百分比
(43)
式中:vmax、vmin分别为无任何减振控制方法时执行器速度的最大值和最小值;v′max、v′min分别为有减振控制方法时执行器速度的最大值和最小值。
表2给出了4种工况下,采用不同控制方法时挖掘机动臂液压缸的仿真数据对比。由表2可知,采用非线性滤波器控制方法能使速度振荡降低32.5%~64.7%,而阻尼补偿控制方法仅能降低20.3%~35.3%。相较于阻尼补偿控制方法,非线性滤波器控制方法可大幅减小速度振荡与压力波动。

表2 4种工况下3种控制方法的动臂液压缸速度最大值、最小值及振荡比Table 2 Velocity oscillations of the boom actuator under different working conditions
为验证所提方法在不同信号突变时的有效性,对突变信号为斜坡信号时动臂液压缸的特性曲线进行了仿真模拟。由于挖掘机斗杆液压缸的初始位置为全缩状态时,其等效负载质量远大于斗杆液压缸的初始位置为全伸状态工况,此时产生的振荡更加剧烈,也更加考验抑振方法的有效性。选择动臂液压缸为研究对象,分别在斜坡信号、低速(0.02 m/s)(定义为工况5)以及斜坡信号、高速(0.06 m/s)(定义为工况6)下,采集执行器的速度、进油腔压力及进口阀信号的仿真数据,如图8所示。由图可知,斜坡信号下,采用非线性滤波器控制方法可使速度振荡降低45.9%~46.1%,而利用阻尼补偿控制方法仅可使速度振荡降低25.6%~29.0%。
综上所述,相较于无非线性滤波器与阻尼补偿方法,利用非线性滤波器可有效减小突变信号下的速度振荡,有效提高不同负载工况下挖掘机负载口独立控制系统动态性能。
5 结 论
本文基于负载口独立控制系统压力流量复合控制策略,提出了采用非线性滤波器修改参考流量信号的控制方法,改善了执行器的运动特性,得到主要结论如下。
(1)基于负载口独立控制系统压力流量复合控制策略,提出了非线性滤波器控制方法,给出了非线性滤波器边界设计原则,并通过修改参考流量信号降低了突变信号对执行器速度的影响。
(2) 采用20 t挖掘机开展仿真,结果表明:所提出的非线性滤波器修改期望流量信号的控制方法,可在不同负载及速度工况下有效降低控制信号突变时执行器的速度波动,动臂全伸、全缩工况下的速度振荡降低了32.5%~64.7%,速度收敛较快。相比于传统阻尼补偿方法,采用所提方法能够有效降低信号突变引起的执行器速度振荡与压力波动。
本文的研究对象为单执行器,对于复合动作而言,仅适用于进口阀为流量控制的执行器。当流量充足时,执行器间流量相互解耦,可应用此方法抑制执行器的速度振荡;对于欠流量工况,此方法仅适用于轻载执行器,而是否适用于重载执行器,则需要进一步研究。因此,未来还需进行更多测试,以验证此方法在复合动作下的有效性。
