采用AK-MCS的燃气轮机轮盘疲劳寿命预测及可靠性评估
2024-04-10罗宇轩李金星赵名星谢永慧张荻
罗宇轩,李金星,赵名星,谢永慧,张荻
(西安交通大学能源与动力工程学院,710049,西安)
燃气轮机是一种先进的动力装置,目前已经在船舰、电力、石油化工和分布式供能等诸多领域得到了广泛应用。轮盘作为燃气轮机的核心部件,其工作寿命与可靠性直接影响到整个机组的安全性能[1]。传统的寿命分析方法将燃气轮机轮盘所处的工作条件视为持续不变的理想工况,而受制于加工工艺、材料的不均匀性、复杂多变的工作环境等诸多因素,轮盘的材料参数、载荷难免存在一定的不确定性因素,由此直接导致传统方法预测出来的轮盘寿命精确度偏低。因此,充分地考虑轮盘运行时伴随的不确定性因素,对轮盘进行精确地疲劳寿命预测及可靠性评估具有重要的研究意义和工程价值。
国内外学者对轮盘低周疲劳寿命预测和可靠性分析展开了一系列研究,最常用的方法主要包括近似分析法、抽样分析法、基于代理模型的分析方法等[2]。其中,采用代理模型的分析方法因极大简化流程的复杂度、显著提高分析效率而得到快速发展。Bai等[3]提出了一种基于概率分析法的响应面技术,对轮盘结构进行了整体可靠性评估和灵敏度分析;Huang等[4]采用Kriging代理模型分析了轮盘的模糊失效概率,探究了输入变量对模糊失效概率的影响;Ji等[5]将Kriging模型与遗传算法相结合,完成了轮盘的结构优化设计,提高了转子结构的可靠性。
代理模型可精确描述输入与输出之间的关系,但往往需要大量工程数据进行拟合,计算效率低下, 尤其面对一些复杂的功能函数,搭建代理模型所需的成本非常高。因此,在确保可靠性分析精度的同时,需要尽可能减少建立代理模型所需样本数,提高模型搭建效率。
主动学习是一种在局部区域内逐步增加样本来提高拟合精度的有效手段。近年来,采用主动学习和代理模型结合的方法研究逐步深入,如基于Kriging模型的主动学习法(AK-MCS)[6-7]、基于交叉验证方差(CVV)的主动学习法[8]、基于神经网络的主动学习法[9]等。其中,以Kriging模型为代表的主动学习方法研究较多,该方法因构造代理模型成本较低,计算效率及准确性较高,能很好地适应疲劳寿命可靠性研究需求。
本文采用AK-MCS算法,充分考虑燃气轮机服役时轮盘伴随的多种不确定性因素,搭建了考虑多源混合不确定性的高精度轮盘低周疲劳寿命预测代理模型,建立了综合轮盘结构分析、低周疲劳寿命预测以及寿命可靠性评估及灵敏度分析一体的仿真流程,并以某型燃气轮机轮盘为例完成了轮盘的低周疲劳寿命预测及可靠性评估,为工程中燃气轮机轮盘的结构设计提供参考。
1 数值方法
1.1 低周疲劳基本理论
疲劳是材料在循环载荷的作用下,某个部位或多个部位造成累积损伤,经过一定周期后发生裂纹或完全断裂的现象[10]。当载荷水平较高时,材料循环应力较高,塑性变形为主,导致结构寿命较短,该情况称为低周疲劳或低循环疲劳。
燃气轮机轮盘在高速运转及承受复杂载荷的过程中产生应力集中,进而会发生较大变形。循环周次不断增加的过程中,轮盘表面会产生裂纹,逐步扩展直至断裂。
1.2 轮盘低周疲劳寿命预测方法
低周疲劳寿命预测是对零部件低周疲劳损伤前有效工作时间的量化。对于燃气轮机轮盘,主流的寿命预测方法包括名义应力法、局部应力应变法等[11]。名义应力法将材料、载荷、应力集中系数相同的结构视作寿命相同,在分析发生弹性变形为主的结构时预测值更加准确,因此更适用于高周疲劳寿命的预测[12]。而局部应力应变法将材料、最大应力、最大应变相同的结构视作寿命相同,将局部的应力、应变代替结构整体的应力、应变进行寿命计算,其流程如图1所示。燃气轮机轮盘的疲劳失效模式以低周疲劳为主,因此局部应力应变法更加契合低周疲劳寿命预测的适用场景。

图1 局部应力应变法轮盘疲劳寿命预测流程Fig.1 Process for predicting fatigue life of wheel discs using local stress-strain method
Manson-Coffin公式是目前应用范围最广的疲劳寿命预测模型,是局部应力应变法的应用代表[13]。该模型综合考虑了材料发生塑性变形和弹性变形两种情况时的疲劳过程,其具体表达式为
(1)
式中:Δεt为应变范围;Δεe为弹性应变;Δεp塑性应变;σf为疲劳强度系数;E为弹性模量;Nf为疲劳寿命;b为疲劳强度指数;εf为疲劳延性系数;c为疲劳延性指数。
Manson-Coffin公式结构形式简单,参数容易获得,但公式应用时并未考虑不同平均应力的影响。在此基础上,Gerber弹性应力修正模型表达式[14]为
(2)
文献[15]引入了材料常数γ,用来表述材料对平均应力影响的敏感程度。文献[16]提出了一种用来计算γ的模型公式,将γ通过材料的屈服极限σ0.2和抗拉强度σb的描述得到,并且通过实验对公式进行验证,γ的表达式为
(3)
将式(3)代入式(2),可得到寿命公式
(4)
1.3 低周疲劳寿命可靠性分析方法
1.3.1 可靠性分析方法
可靠性分析是判断轮盘寿命信度、衡量轮盘工作稳定性的重要一环,核心过程是以给定的不确定性输入来量化不确定性输出。常见的分析方法包括蒙特卡罗法、基于敏感度的方法、基于代理模型的方法、剩余强度法等。
采用商用软件进行有限元分析的方式成本高、耗时长,在算例较多的情况下效率低下。而代理模型可以精确地描述输入与输出之间的关系,通过建立代理模型将输入参数与输出数据有效拟合,构造高精度的函数关系,代替复杂耗时的数值分析模型,可极大缩短计算时间,提高分析效率。
燃气轮机轮盘的低周疲劳寿命Nf往往受到材料属性、工作载荷等多种随机因素的影响,随机变量的分布情况可以表示为
X=[X1,X2, ,Xn]T
(5)
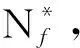
(6)
Pf=P{f(x)≤0}
(7)
(8)
式中:P{·}为概率算子[17];qx(x)为变量X的联合概率密度函数。
本文采用AK-MCS作为联接不确定性输入与输出的代理模型,并以有理二次核作为该模型的核函数。Kriging代理模型采用高斯回归过程模型[18],因该模型在提供预测位置点输出值的同时,还可提供不确定性的估计方差,具有精确插值与随机特征属性,预测精度高、适用性好,预测结果与真实值更为接近。
1.3.2 Kriging模型
Kriging模型采用高斯随机过程模型,是一种高效的插值方法,模型由多项式和随机因式两部分构成,即
y(x)=gT(x)β+z(x)
(9)
式中:g(x)为模型的基本函数;β为回归系数;z(x)为高斯随机过程。均值为0,协方差为
Cov[z(xi),z(xj)]=σ2R(xi,xj;θ)
(10)
(11)
式中:σ为z(x)的标准差;R(xi,xj;θ)为高斯相关函数;m为该向量内元素编号。
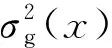
(12)
rT(x)R-1r(x)]
(13)
(14)
式中:G为回归矩阵;θ由极大似然估计获得
(15)
1.3.3 可靠性分析流程
本文采用基于AK-MCS轮盘低周疲劳寿命可靠性评估方法,可靠性分析流程如图2所示,具体步骤如下。
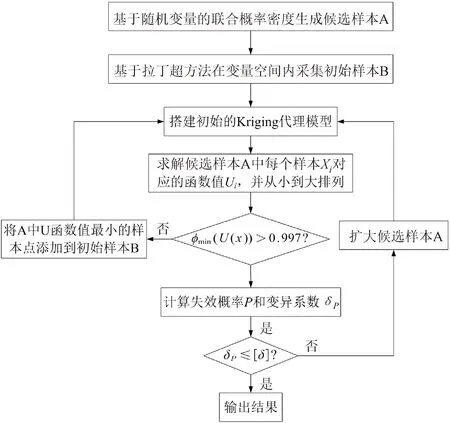
图2 基于AK-MCS的轮盘低周疲劳寿命可靠性分析流程图Fig.2 Flow chart of reliability analysis for low-cycle fatigue life of wheel disc based on AK-MCS
步骤1:基于随机变量的联合概率密度函数生成大量的候选样本A。
步骤2:采用拉丁超立方采样法在变量空间内采集少量样本B作为初始样本。
步骤3:根据初始样本B和其对应的功能函数值,搭建初始Kriging代理模型。
步骤4:根据主动学习函数
(16)
求解候选样本A中每个样本Xi的学习函数值Ui,将迭代过程中学习函数值最小的样本点作为插值依次添加到样本B中,满足插值结束条件φmin(U(x))>0.997时,加点停止,主动学习结束,确定最终样本集S。
步骤5:计算轮盘疲劳寿命的失效概率和变异系数,判断现有代理模型是否达到要求。若达到要求,则用该代理模型对轮盘寿命可靠性进行评估,并输出结果;若未达到要求,则重新插值迭代。
1.3.4 Sobol’灵敏度分析方法
2001年,俄罗斯学者Sobol’[19]提出了一种全局灵敏度分析方法。假设输入参数X为M维向量组,即X={x1,x2, ,xM},概率密度函数f(x)为
+f1,2,,M(x1,x2, ,xM)
(17)
(18)
式中:f0为f(x)在DX上的积分。
函数f(x)展开后的每一项为相互正交的关系,可以通过积分形式表达,即
(19)
f0-fi(xi)-fj(xj)
(20)
f(x)的总方差D为
(21)
偏方差为
Di1,i2,,is=
(22)
式中:1≤i1≤is≤M;s=1,,M。
则Sobol’灵敏度指数表达式为
(23)
该指数含义为每组随机变量对总方差D的影响程度。与一个输入变量相关的指数称为一阶Sobol’指数Si,f,它代表该输入变量单独的影响;与多个输入变量相关的指数被称为高阶Sobol’指数,高阶指数需要考虑多个变量之间的相互作用关系,而不能被分解为单一变量的影响。
全局Sobol’指数Si,t是涉及某个随机变量的Sobol’指数总和
(24)
式(24)的计算需要通过局部灵敏度计算单个随机变量的Sobol’指数。
若通过Si,n来表示除了变量xi以外的所有变量总体Sobol’指数,即
Si,n=Sv
(25)
式中:下标v=1,,i-1,i+1,,M。
全局Sobol’指数Si,t可以写为
Si,t=1-Si,n
(26)
2 结果与讨论
2.1 透平轮盘模型及有限元分析
本文研究的某型燃气轮机透平轮盘模型如图3所示。轮盘为周期循环对称结构,整圈轮盘的轮缘上包含90个轮槽用于固定透平叶片。选取整体模型的1/90扇形区域进行有限元分析,扇形角为4°,其中蓝色端面为扇形区域的旋转周期面。

图3 某型燃气轮机轮盘模型Fig.3 The certain type of gas turbine disc model
本文以GH4169材料作为透平轮盘的铸造材料,该材料是镍基高温合金中应用最多的材料之一,在高温条件下强度高、稳定性强、硬度高,常用于燃气轮机、航空发动机中透平轮盘、传动轴等核心部件制造[20]。GH4169材料的力学性能参数[21]如表1所示。
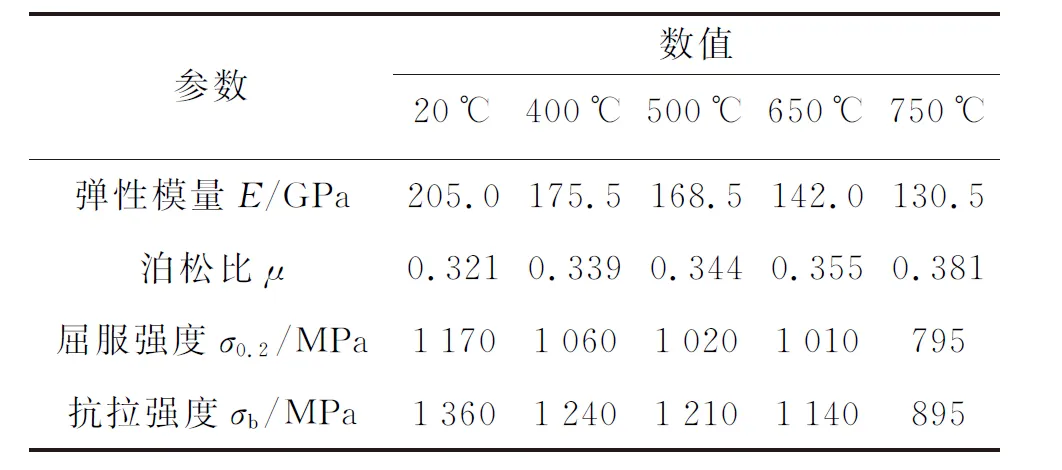
表1 GH4169材料力学性能参数Table 1 Mechanical performance parameters of GH4169
采用APDL软件对轮盘整体采用四边形网格划分,网格划分与边界条件如图4所示,具体设置如下:①在进气侧端面,轴向、周向位移约束;②在出气侧端面,周向位移约束,轴向位移耦合;③在轮毂下端面,径向位移约束;④在旋转周期面,周向位移约束。

(a)边界条件
透平轮盘的离心载荷、轮槽齿面接触压力、预紧压力等对轮盘的结构性能的影响起主导作用。轮槽齿面接触压力由透平叶片旋转产生的离心力FTHB作用在与叶根直接接触的3对轮槽齿面上产生,轮槽齿面及接触压力示意如图5所示,图中F1、F2、F3代表与叶根与直接接触的3对齿面产生的接触压力,且与轮槽底面的夹角为θTB。
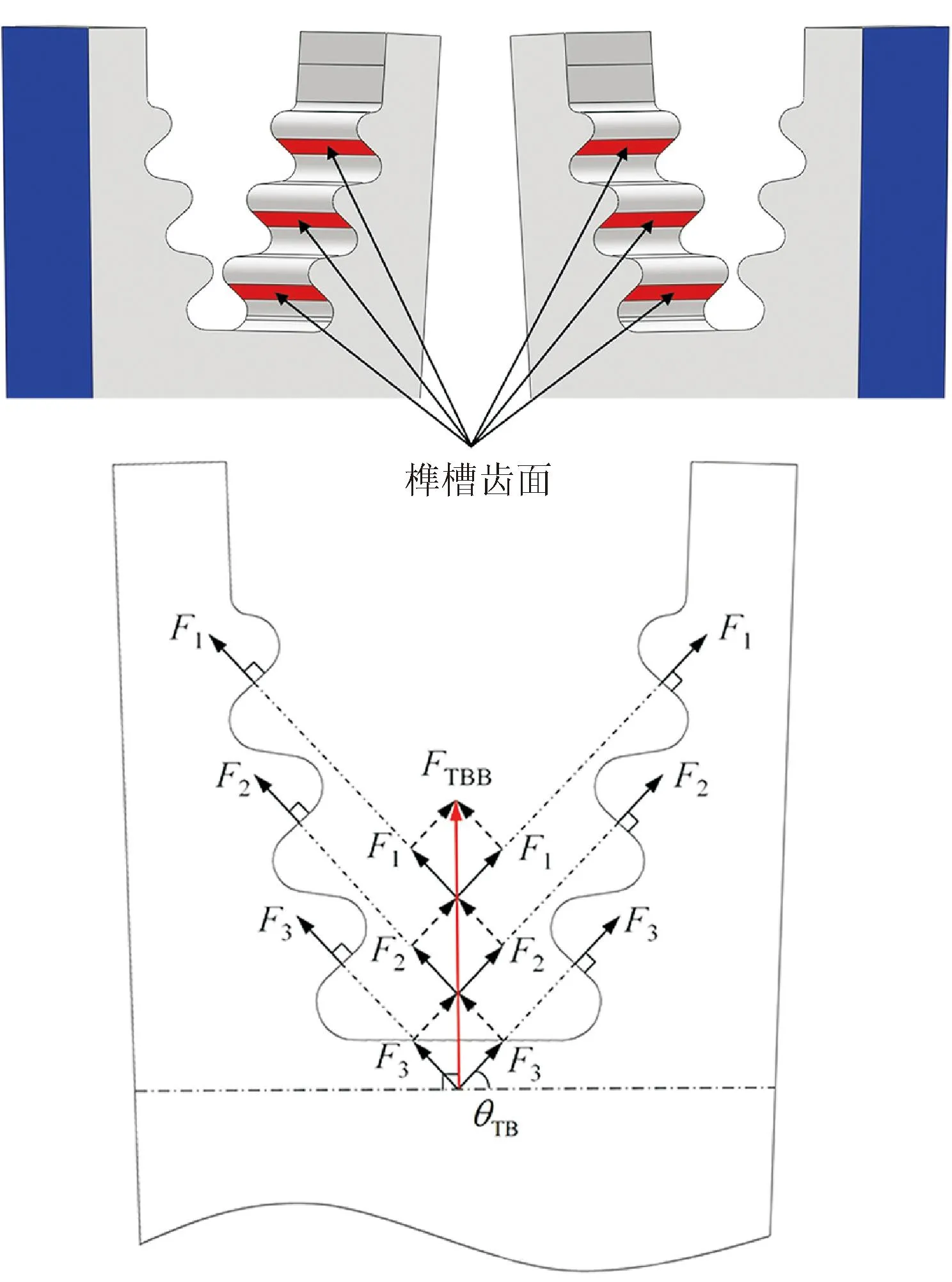
图5 轮槽齿面及接触压力示意图Fig.5 Schematic diagram of wheel groove tooth surface and contact pressure
考虑到燃气轮机透平的进气温度较高,透平轮盘整体温度也较高,因此本文在对透平轮盘进行有限元分析时,除了考虑离心载荷、轮槽齿面接触压力以及预紧压力的作用之外,还考虑了温度载荷的作用。轮盘的温度随半径尺寸的分布如图6所示,任一点温度T可由如下的经验公式[22]给出
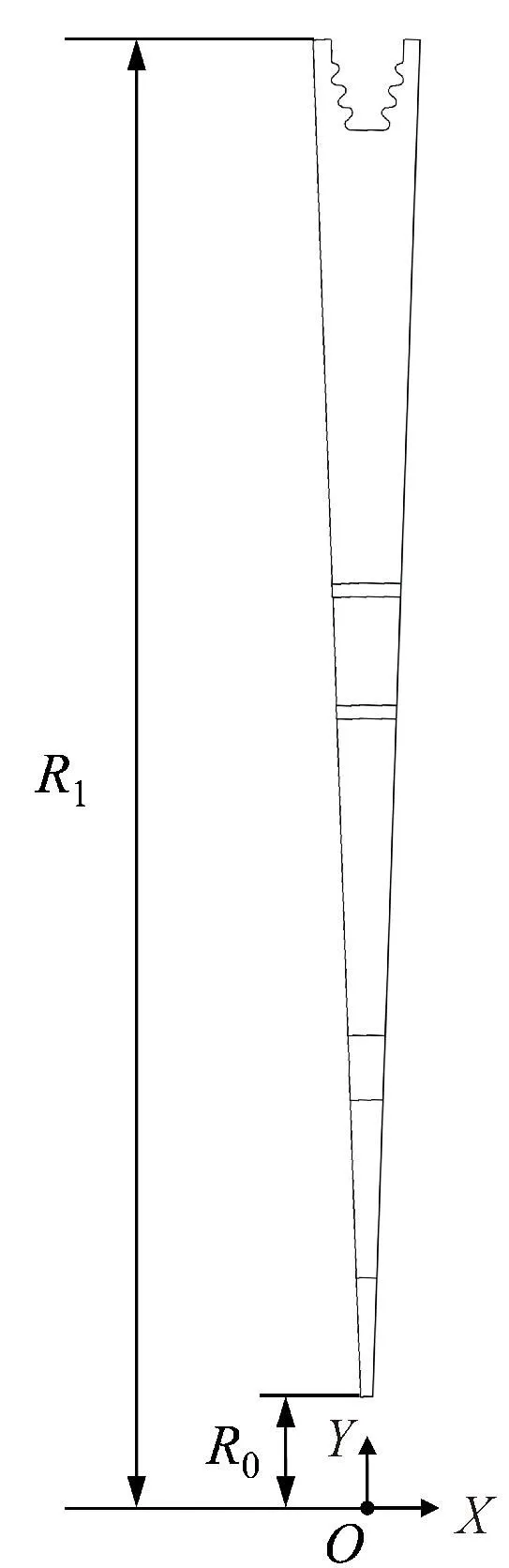
(a)轮盘尺寸
(27)
式中:T0为轮毂温度;ΔT为轮缘与轮毂的温度差;R为任一点轮盘半径;R0为轮盘内径;R1为轮盘外径。
轮盘载荷的具体数值如下:轮盘给定旋转角速度n=3 000 r/min;假定3对接触齿面的轮槽齿面接触压力相等,轮槽齿面接触压力PTB2=364.3 MPa;轮盘在装配过程中,受到多级轮盘的轴向挤压力,作用位置为轴向轮盘连接端面,本文假定轴向预紧力FTB1=80 MPa施加在透平轮盘进气侧端面。
图7展示了轮盘等效应力及应变分布的计算结果。从图7可以看出:轮盘透平轮盘的等效应力、应变整体呈现出轴向对称的分布特征;轮盘下方的圆角处、轮盘中段下端的圆角处均有明显的应力集中,这两处的等效应力相近,处于601.992~687.755 MPa之间;轮盘中段上端的圆角处也存在一定的应力集中,但应力水平不高。
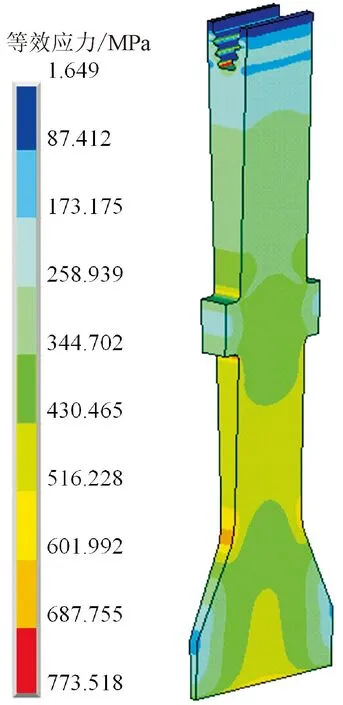
(a)等效应力
图8展示了轮盘轮槽局部位置的应力及应变分布。可知由于轮槽齿面接触压力的影响,3对齿面均存在明显的应力集中,该应力为透平叶片旋转挤压接触齿面而产生的压应力。由于第1对、第2对齿面下方的圆角在受到拉伸时,将应力传递给了第3对齿面,由此导致第3对齿面应力水平非常高。因此,将第3对齿面下方的圆角处视作透平轮盘疲劳失效的局部危险点。
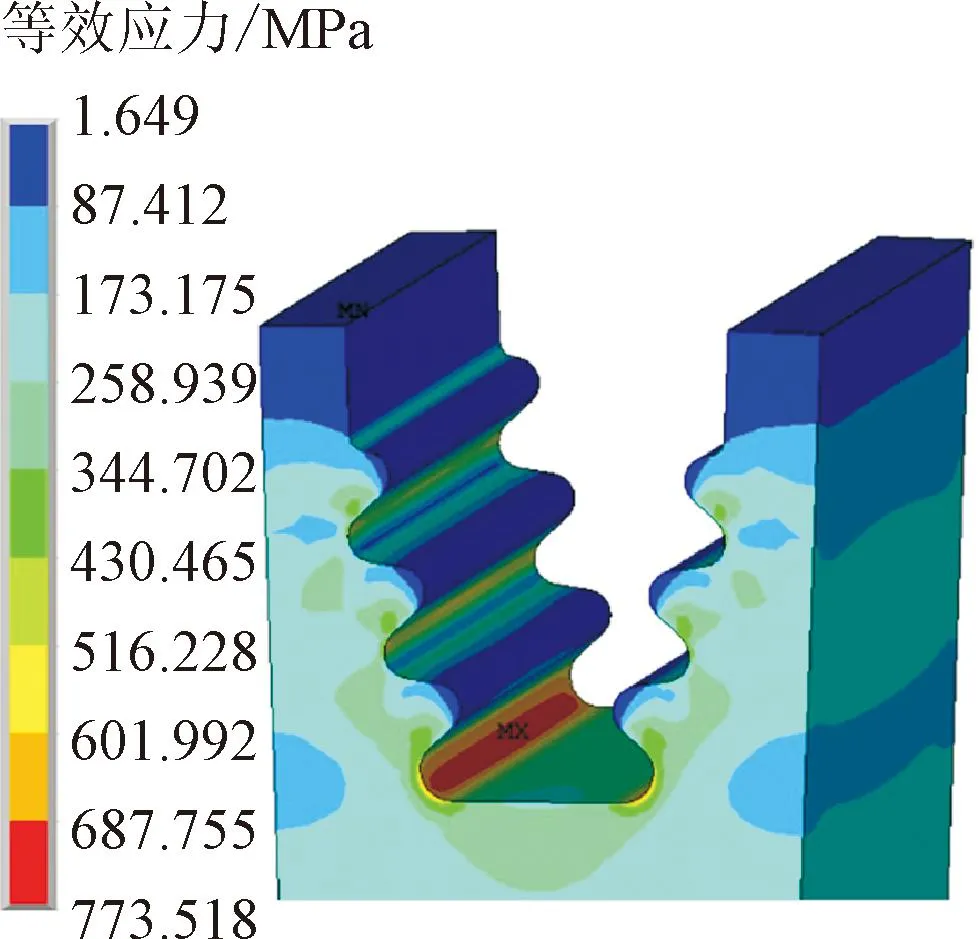
(a)等效应力
运用式(4)计算轮盘寿命,代入轮盘局部危险点的4个材料参数E、μ、σb、σ0.2及5个疲劳性能参数σf、εf、b、c。其中疲劳性能参数按照GH4169材料的经验参数给定,具体取为1 651 MPa,0.278,-0.09,-0.56。又由于透平轮盘温度较高,材料参数随温度变化太大,因此需要先根据式(27)计算得到局部危险点温度值,再带入透平轮盘局部危险点的旋转半径Rd,可以计算得到局部危险点温度Td=527.8℃,此温度下的材料参数无法直接获取,需要根据温度区间进行估值。
选取GH4169在温度T1=400℃、T2=500℃、T3=650℃的材料参数作为线性插值的端点,并按照表2进行参数符号的命名,各参数的具体数值参考表1。

表2 透平轮盘材料参数符号命名Table 2 Nomenclature of material parameter for the turbine disc
插值公式为
(28)
以T2、T3作为插值端点,图9给出了插值得到局部危险点温度Td下的材料参数的过程。
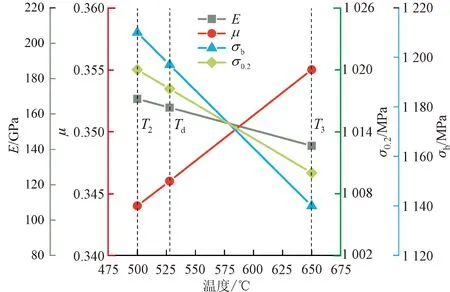
图9 轮盘局部危险点GH4169材料参数插值情况Fig.9 Interpolation of GH4169 material parameters at local danger points on the turbine disc
根据上述寿命预测模型及疲劳性能参数及插值得到的材料参数,在最大转速为3 000r/min的启停工况下,最终计算得到的透平轮盘Nt为1.177×104周。
2.2 不确定性因素分析
工程中,考虑影响燃气轮机轮盘工作寿命的不确定性因素主要包括几何尺寸、材料属性、工作载荷等类别。根据燃气轮机轮盘的工作特点,本文选取3类随机因素作为输入参数展开详细分析[23-24]。
(1)力学性能参数。由于材料加工误差及工作状态变化,材料的力学性能参数往往在一定的区间范围内变化。选取弹性模量、泊松比、抗拉强度3种具有代表性的力学性能参数作为随机变量开展研究,认为其服从正态分布[25]。
(2)疲劳性能参数。在计算轮盘疲劳寿命时所用到的4种疲劳性能参数是预测轮盘寿命要用到的重要参数,对轮盘寿命的可靠性评估有重要影响。本文选取该4种疲劳性能参数作为随机变量,认为其服从正态分布。
(3)载荷类参数。轮盘处于循环启停的变转速条件下工作,因此转速对于轮盘是一个重要的影响因素,通常情况可以将转速设定为正态分布[26];此外,轮盘受到较大的预紧压力载荷和轮槽齿面接触压力载荷,本文同样将其按照正态分布处理。
2.3 轮盘低周疲劳寿命可靠性分析
对于燃气轮机透平轮盘而言,本文选定GH4169在400℃下的弹性模量E1、泊松比μ1、500℃下的弹性模量E2、泊松比μ2、650℃下的弹性模量E3、泊松比μ3、抗拉强度σb、转速n、预紧压力PTB1、轮槽齿面接触压力PTB2、疲劳强度系数σf、疲劳延性系数εf、疲劳强度指数b、疲劳延性指数c共14种参数作为不确定性输入,均视为正态分布。采用变异系数ρ描述样本数据的离散程度,采样标准如表3~5所示。

表3 透平轮盘力学性能参数采集标准(ρ=0.01)Table 3 Standard for collecting mechanical performance parameters of turbine disc (ρ=0.01)

表4 透平轮盘疲劳性能参数采集标准(ρ=0.01)Table 4 Standard for collecting fatigue performance parameters of turbine disc (ρ=0.01)

表5 透平轮盘载荷参数采集标准(ρ=0.02)Table 5 Standard for collecting load parameters of turbine disc (ρ=0.02)
根据表3~5所示的采样标准,按照透平轮盘各输入参数的概率密度随机生成1×105组备选样本集;同时通过拉丁超立方抽样法在给定区间内完成20组初始输入参数采样,作为初始样本集。
初始样本采集完成后,在MATLAB控制器上通过自编程序实现ANSYS软件的调用,完成20组不同工况的轮盘强度计算,提取各个工况下局部危险位置对应的循环应力幅。采用基于U函数的AK-MCS算法,根据GH4169低周疲劳ε-N方程计算得到各个工况下的轮盘低周疲劳寿命,构建初始Kriging代理模型。
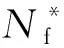
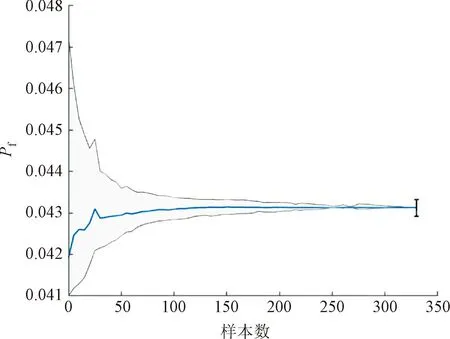
图10 失效概率的收敛曲线Fig.10 Convergence curve of failure probability
图11展示了备选样本集全部样本经由AK-MCS代理模型计算得到的透平轮盘疲劳寿命分布情况。其中,直方图表示的是计算得到的真实结果,可以发现,透平轮盘的寿命分布同样表现为中间集中、两侧不对称,且中间峰值偏向于左侧的分布特点,该分布特征与对数正态分布极其相似,因此采用对数正态累计分布函数(LogNormal)对寿命分布进行拟合,同样给出了LogNormal拟合曲线。
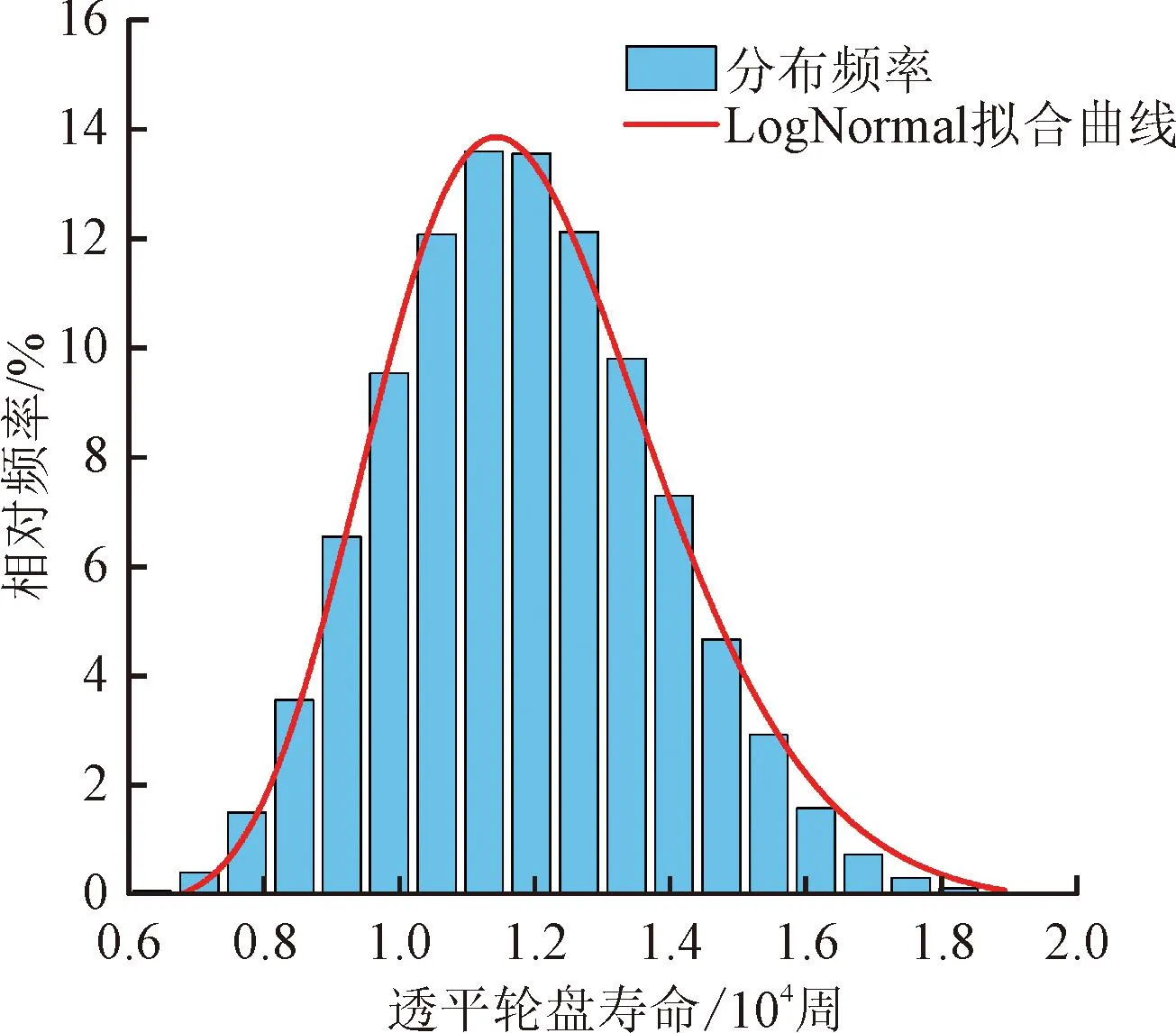
图11 透平轮盘寿命分布Fig.11 Life distribution of turbine disc
得到透平轮盘寿命的分布后,可由式(8)及失效概率与可靠度的互补关系计算得到透平轮盘失效概率及可靠度与寿命的分布。图12展示了失效概率、可靠度与寿命的累积分布曲线,图12中散点为透平轮盘在不同寿命取值下对应的失效概率、可靠度计算结果。

(a)失效概率分布
2.4 灵敏度分析
本文采用Sobol灵敏度分析方法对上述透平轮盘的14种随机输入参数进行了全局灵敏度分析,输入参数的分布情况与表3~5的采样标准一致。
图13、图14直观地给出了透平轮盘关于14种随机输入参数的Si,f及Si,t分布情况,透平轮盘的3类输入参数中,载荷类参数对轮盘的疲劳寿命影响最明显,其中影响程度最大的是PTB2,其次是n,PTB2和n的Si,f及Si,t计算结果要远高于其他参数,对轮盘的疲劳寿命起着决定性的作用。
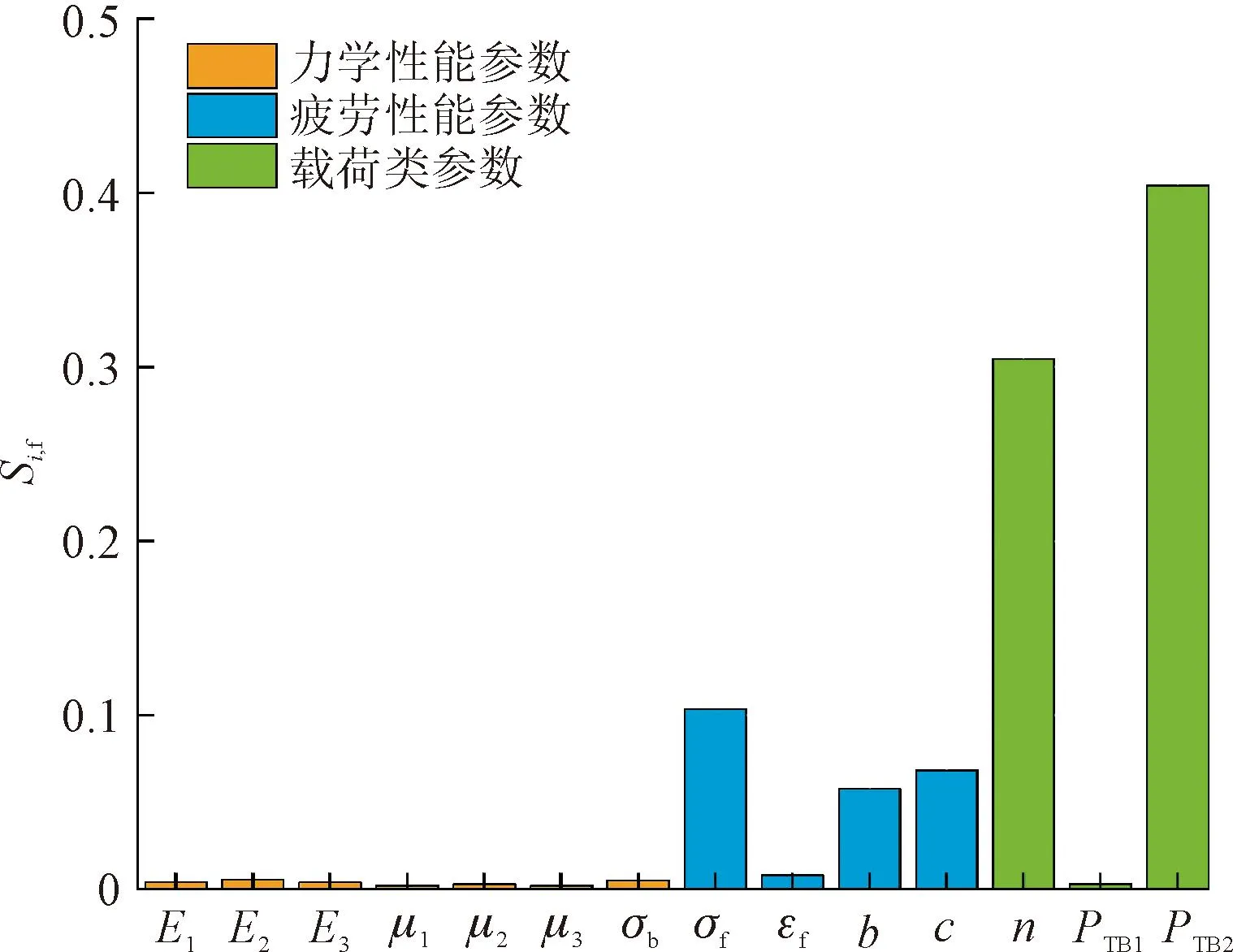
图13 一阶Sobol’指数Fig.13 First order Sobol’ index
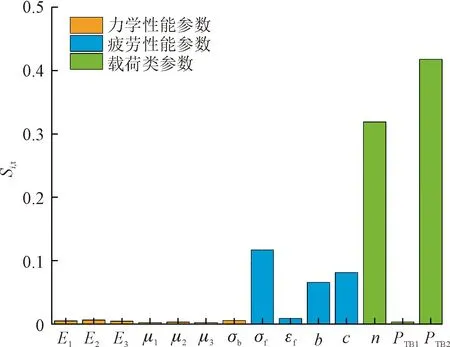
图14 Sobol’总指数Fig.14 Sobol’ total index
在4种疲劳性能参数中,σf、c和b对轮盘的疲劳寿命的影响程度要明显高于εf;其余参数的变化对透平轮盘的疲劳寿命影响程度很小。在透平轮盘的疲劳寿命可靠性研究中,必要情况下可以忽略灵敏度指标较低参数的影响。
3 结 论
本文以某型燃气轮机透平轮盘为研究对象,考虑实际工况下伴随的多元混合不确定性因素,对寿命的可靠性进行合理评估;基于主动学习代理模型,搭建了一套完整的轮盘低周疲劳寿命可靠性分析流程,完成了某型燃气轮机轮盘低周疲劳寿命可靠性评估及灵敏度分析,主要结论如下。
(1)对轮盘确定性结构分析的结果表明,在3 000 r/min 的工况下,轮盘应力整体呈现轴向对称的分布情况,其第3对齿面下方的圆角处产生了极其明显的应力集中,对应最大等效应力值为773.518 MPa,最大应变值为0.004 73,局部危险点位于轮槽第3根齿面下方的圆角处。
(2)通过自编程序完成了多源不确定性因素作用下的某型燃气轮机轮盘低周疲劳寿命预测以及寿命可靠性评估,得到轮盘的寿命预测结果为1.177×104周。
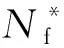
(4)通过对影响轮盘疲劳寿命的输入参数进行灵敏度分析,发现载荷类参数对轮盘的疲劳寿命影响最明显,其中影响疲劳寿命最大的输入参数是轮槽齿面接触压力。
