变压器全生命周期成本分析及优化

桂芳旭，陈衡，赵欣悦，潘佩媛，辛诚，姜雪

(1.华北电力大学，北京 102206；2.国网经济技术研究院有限公司，北京 102209；3.国网辽宁省电力有限公司经济技术研究院，辽宁 沈阳 110016)

电网设备的全生命周期评估涉及初始投资、运行、检修、故障处置及资产报废回收等各阶段。在电网设备全寿命周期评估方法中，应用较多的是基于LCC(life cycle cost，LCC)的评估方法。与此同时，电网设备LCC评估的主要依据是电网设备LCC的最小化[1-3]。电力变压器是电网中的核心能量转换设备，在电力系统中发挥着重要作用。近年来，我国电力需求快速增长，电网的高速建设和投资拉动了输变电设备的市场需求。巨大的电力建设投资给变压器行业带来了机遇和挑战，促使变压器行业得到快速发展。特别是西电东送、南北互联、跨区联网等工程的加快建设，带动了我国电力变压器行业的快速发展[4-5]。因此，如何优化变压器的LCC，提高电网的经济效益是当前人们关注的热点。

变压器的资产全生命周期管理需要庞大的数据支撑，数据之间关联密切，因此成本管理并不能一蹴而就，需要先建立变压器LCC的数学模型，再对变压器的成本进行分析，然后通过这些具体的成本分析对变压器LCC进行优化[6]。因此，如何建立一个科学精确的变压器LCC模型，并分析其成本获得规范合理的优化结果，已经成为近些年国内外学者讨论的焦点。

关于变压器LCC建模计算的研究，国内外学者已经取得了一定的成果。赵宇琪等[7-9]基于电力变压器的数据集构建了算法优化支持向量回归的电力变压器LCC预测模型，并对该模型进行了算例仿真。刘鹏飞等[10-11]从提高规划方案可比性入手，提出各类项目效益的识别方法、电网LCC和效益量化方法，进而建立成本计算模型和效益计算模型。何永秀等[12-13]提出基于变压器状态模拟的全寿命周期费用分析模型，在该模型中，将变压器的运行状态划分为可用与不可用两种。卞建鹏等[14-15]从LCC的角度出发，建立了役龄回退模型，并应用搜索算法对变压器检修成本模型进行了优化。Mohsen等[16-17]通过设置目标函数来优化电力设备的成本和寿命损失；Chen等[18-19]提出将环境成本适当地引入电力公司实施的生命周期成本计算中。Li等[20-21]对电力设备LCC进行建模，并进行了受其他成本因素变化影响的敏感性分析。

综上所述，国内外学者在变压器LCC模型的建立及应用方面做了大量的研究，提出了多种算法来优化成本。但是，一方面对变压器LCC分析的研究不够全面，许多案例中没有考虑到成本影响因素，例如电压等级等；另一方面，算法更新迭代的速度非常快，一些优化算法已经有一定的年份，优化精确度大大降低，不再适合继续用来优化变压器LCC模型。为了更加全面地分析变压器LCC，并获得更加科学的优化结果，本文通过整理和计算大量具体数据，对变压器不同电压等级下的成本变化规律及LCC的比例进行分析，同时采用最近几年新提出的鲸鱼优化算法(whale optimization algorithm，WOA)来优化变压器LCC模型，这对于实际工程中变压器成本管理决策有一定的指导意义。

1 变压器LCC建模

根据LCC理论，为明确资产全寿命周期的成本类型、实现生产成本量化分析应用，LCC计算将成本拆分为5个阶段进行计算：初始投资(C1)、运维成本(C2)、检修成本(C3)、故障成本(C4)与回收处置成本(C5)。本文成本建模采用的方法是现值法，考虑社会折旧率R和通货膨胀率r，可构建出变压器LCC[22]

CLCC=C1+C2+C3+C4+C5.

(1)

1.1 初始投资成本

初始投资成本C1可以分为3类：采购建设成本；财务成本；安装、调试、培训成本。采购建设成本包括对项目进行评估时土地、建筑咨询费和购买设备等费用；财务成本包括与资金替代效应有关的花费，一般是由贷款带来的利息支出；其他成本包括安装调试机器的费用和培训工人的费用[23]。

C1=Ccg+Ccw+Caz+Cts+Cpx.

(2)

式中：Ccg为采购建设成本；Ccw为财务成本；Caz为安装成本；Cts为调试成本；Cpx为培训成本。

1.2 运维、检修成本

以“项目+工单”为分析单元，“设备维修清册”为手段，采用归集为主、分摊为辅的设备层成本量化原则，实现设备层成本量化。因运维成本和检修成本统一核算、无法分割，将其合并计算，运维检修成本可分为变压器能耗成本C2和变压器运行人工维护成本C3[6]。

C2+C3=Cnh+Cwh.

(3)

式中：Cnh为变压器能耗成本；Cwh为变压器运行人工维护成本。

1.2.1 变压器能耗成本Cnh

变压器损耗包括空载损耗和负载损耗2个部分，因此变压器能耗成本

(4)

式中：a为电价水平，一般取0.47～0.5，本文具体取值为0.48；P0为空载损耗；Pk为负载损耗；AF为可用系数，一般取1；T为年运行小时数，取8 760；K为负载率，一般取0.5～0.65，本文具体取值为0.6[6]；R为社会折现率；r为通货膨胀率；N为计算时选取数据的年份总和。

1.2.2 变压器运行人工维护成本Cwh

(5)

式中：Cwh(t)为第t年设备的运行维护成本。

1.3 故障成本

故障成本C4可以分成3类：抢修成本、负荷损失费和重要用户赔偿。

C4=Cqx+Cfhss+Cyhpc.

(6)

式中：Cqx为抢修成本；Cfhss为负荷损失费；Cyhpc为重要用户赔偿。

故障成本C4通过借鉴生产成本量化成果，由近年同类设备发生的成本费用测算得来，因此故障成本C4和检修成本C3的相关作业被合并统计，成为无法分割的单位。在不影响结果准确的情况下，可以将故障处置成本C4合并至检修成本C3。

1.4 退役处理成本

变压器的退役处置成本C5包括变压器的报废成本和残值。报废成本是指设备在报废后所需要的用于处理废弃设备的费用，电气设备会保留有一定的残值，所以在正常回收后其成本可能为负数，需要结合历史数据进行分析考虑资金的时间效应[24]，所建模型为

(7)

退役处置成本C5可以被归集到企业资源计划(enterprise resource planning，ERP)、电子商务平台(E-commerce platform，ECP)系统的废旧物资处置模块，无法归集的按照初始投资成本的5%进行测算。

2 WOA

近年来，为了让变压器更加平稳、经济地运行，并最大限度地减少变压器的LCC，国内外学者使用不同的优化技术，包括遗传算法(genetic algorithm，GA)[25]、粒子群优化(particle swarm optimisation，PSO)[26-27]和帝国主义竞争算法(imperialist competitive algorithm，ICA)[28]等，以确保变压器组以最佳方式运行。本文采用WOA来优化变压器LCC，通过设置目标函数，确定约束条件找到LCC最佳值，并绘制图表便于直观地展现结果。

WOA是一种由国外学者Mirjalili[29]等提出的新型元启发式优化算法。与现有的元启发式算法以及传统方法相比，WOA具有很强的竞争力，受自然启发的元启发式算法通过模拟生物或物理现象来解决优化问题[30]。

3 算例分析

3.1 不同电压等级下变压器LCC变化规律

由解嘉彬等[31-32]提出的观点可以知道，电压等级对于变压器至关重要，它直接影响到电能的传输效率、电网的稳定性、设备的兼容性以及系统的安全性和维护成本。适当选择和配置变压器的电压等级对于实现高效、可靠和安全的电力系统至关重要[33]。以下将采用图表的形式，对数据深入分析，以便更专业地探讨这一问题。

图1对比了北方某地区多所变电站的5种变压器的LCC，可以明显看到不同电压等级对LCC的影响：在电压等级低于330 kV时，随着电压等级的提高，箱线图的箱宽越来越大，即设备LCC波动越来越大；在电压等级等于330 kV时，设备LCC波动范围达到最大，在60.82万元至677.83万元间波动，中位线位于均值下侧，小于均值，该数据集呈正偏态分布，即大部分330 kV变压器LCC都低于均值，但成本较高的数据对总体数据的影响效果较为明显；在电压等级达到750 kV时，箱宽变窄，即设备LCC更加集中，波动范围也较330 kV缩小近51%。四分位距(interquartile range，IQR)是一种通过将数据集划分为四分位数来实现异常值检测的统计方法。四分位数也称四分位点，是指在统计学中把所有数值由小到大排列并分成四等份，设3个分割点位置的数值为Q1(第1个四分位数)、Q2(第2个四分位数)和Q3(第3个四分位数)。四分位距的值用SIQR表示，将SIQR定义为Q3-Q1，位于Q3+1.5SIQR或Q1-1.5SIQR之外的数据被视为异常值，异常值越多说明尾部越重，自由度越小(即自由变动的量的个数)。偏态表示偏离程度，异常值集中在较小值一侧，则分布呈左偏态；异常值集中在较大值一侧，则分布呈右偏态。图1中：35 kV变压器异常值较少，自由度较大，工程实际中对35 kV变压器的应用比较多；750 kV变压器的异常值较多，自由度较小，工程实际中对750 kV变压器的应用比较少，分布呈左偏态。

图1 5种电压等级LCC对比Fig.1 Comparisons of LCCs for five voltage levels

图2清晰地体现了5种电压等级变压器的实际应用数目、LCC波动程度和平均波动范围，可以看到：35 kV和110 kV变压器的实际应用数目基本是其他电压等级变压器的3倍以上，在实际应用中使用最广泛，而且35 kV变压器的LCC的稳定程度高于其他电压等级，基本稳定在40万元上下，LCC平均值也相对最低。

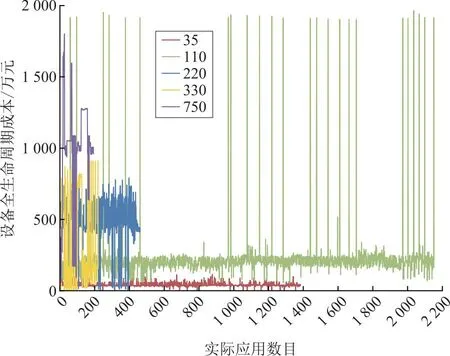
图2 5种电压等级LCC折线图Fig.2 Line diagram of LCCs for five voltage levels

图3采用箱线图和正态曲线拟合表现35 kV变压器LCC的更多细节，如实际应用数目、平均值、中位数和正态分布情况。对其余电压等级数据特点同样进行了图表绘制分析，但为避免篇幅堆叠重复，在表1中对5种电压等级数据特点进行了汇总，可以看到：随着电压等级的提高，实际应用数目整体上呈现下降趋势，110 kV变压器实际应用数目高达2 152个，LCC平均值整体上呈现出上升趋势，35 kV变压器成本平均值最低，为41.40万元；大部分电压等级的LCC中位线位于均值下侧，小于均值，呈正偏态分布，分布的高峰偏下，长尾从下端逐渐延伸于上端；110 kV变压器LCC中位线与均值基本重合，该数据集呈正态分布，大部分与均值基本接近，具有很强的稳定性。

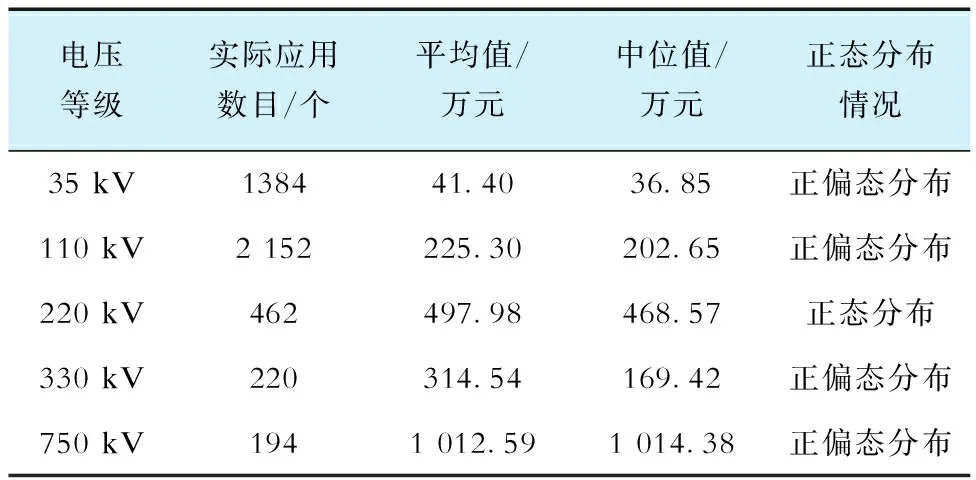
表1 5种电压等级变压器数据特点Tab.1 Transformer data characteristics for five voltage levels

图3 35 kV变压器LCC箱线图Fig.3 Box line diagram of 35 kV transformer LCC

通过5个不同电压等级的变压器LCC折线图、箱线图及拟合曲线，可以清晰地看到，随着电压等级的增加，变压器LCC也在提高，主要原因在于：变压器的核心、绕组、绝缘材料等都需要根据电压等级进行选择和设计，较高的电压等级通常需要更大尺寸和更高品质的材料，这会导致成本增加。

但是，为了降低成本，不考虑其他影响因素和现实条件的情况下，总是选择较低电压等级的变压器是不可行的。首先，较高电压等级的变压器LCC更加集中，波动范围更小，成本数据更加稳定，较高的电压等级可以减少输电线路上的电流，从而降低电线的电阻损耗和传输损耗，这有助于提高电网的效率，并减少能源的浪费；其次，较高的电压等级还可以减少线路电压降和电力系统中的电压波动，有助于保持电网的稳定性。从长远来看，较高电压等级的变压器可能能够节省能源和维护成本。因此，在选择变压器电压等级时，需要综合考虑成本、性能和可行性等因素。

3.2 变压器LCC比例分析

根据上一节对不同电压等级下变压器LCC成本变化规律的分析，选取LCC较低、数据较为稳定的北方某变电站110 kV变压器作为研究对象，该变压器主要参数见表2。图4展示了所选变压器从投运当年到退役当年各部分成本占LCC的比例。

表2 北方某变电站110 kV变压器主要参数Tab.2 Main parameters of a 110 kV transformer in a substation in north China

图4 投运当年到退役当年各部分成本占LCC比例Fig.4 The proportion of each part of the cost to the total LCC from the year of operation to the year of retirement

由图4可以清晰地看到，C1稳定地占据该110 kV变压器LCC的98%；C2+C3+C4在投运第2年、第17年超过C5在LCC中所占份额，C5在投运第10年、第26年超过C2+C3+C4在LCC中所占份额，其余年份二者所占份额差距较小。因此在控制LCC时，应该重点关注C1，科学规划初期方案，高效管理人员设备，尽可能地减少在采购建设、财务管理、人工培训等方面的支出。

3.3 使用WOA优化变压器LCC

根据WOA并通过设置目标函数来优化变压器的成本。由于优化目标是使变压器LCC最低，因此结合第1章得到目标函数为

F=min(C1+C2+C3+C4+C5).

(8)

变压器实际运行需满足一定的可靠性和经济性，且实际参数需满足一定的客观规律。因此目标函数需要有约束条件[16]：

(9)

Ktq×Lt≤Ctq.

(10)

式(9)、(10)中：Q为变电站总数；q表示第q个变电站；Ktq为在(0，1)范围内的随机数；Lt为电网总负荷；Ctq为变电站的额定容量。式(9)规定所有变电站的总负载在优化前后必须相同。式(10)是指变压器的负载不得超过其容量。

为了方便计算，结合第1章将式(8)改写成如下形式：

F=min(C1+Cnh+Cwh+C4+C5)，

(11)

Cnh=CNLL+CLL，

(12)

CNLL=aP0T，

(13)

CLL=aPkTK2.

(14)

式中：CNLL为空载损耗成本；CLL为负载损耗成本；a为电价水平，一般取0.47～0.5 元/kWh；P0为空载损耗，取63.4 kW；Pk取285 kW；T为年运行小时数，取8 760；K为负载率。

为了计算方便起见，将除K以外的所有参数定义为常数，得到一个以负载率K为自变量的目标优化函数。表3列出了3.2节所选北方某变电站110 kV变压器投运30年的LCC平均值。Cnh相较于Cwh来说占比较小，由第1章可知，C4和C3被合并统计，因此C2+C3+C4可近似看作Cwh。

表3 110 kV变压器投运30年的LCC平均值Tab.3 Average LCC value of 110 kV transformer after 30 years of operation

将以上所有数值代入式(11)，得到简化后的目标函数为

F(K)=min (621.95+119.84×K2).

(15)

接下来，使用MATLAB软件并采用WOA对目标函数进行优化。

图5为变压器LCC函数3D图，其中，自变量为负载率K，变压器LCC优化值用F(K) 〔式(15)〕表示，可以得到一个空间三维变压器LCC函数图，以便更加清晰地观察到WOA的寻优过程。由图5可以得知目标函数是一个单峰函数，只有一个全局最优，该函数展现了WOA与其他元启发式算法相比具有更强的竞争力和可利用能力。从曲面的平滑度来看，WOA也是该函数最有效的优化器，或者至少是第二好的优化器[34]。因此，WOA可以为变压器LCC优化提供非常好的优化途径。

图5 变压器LCC函数3D图Fig.5 3D diagram of transformer LCC function

在整个计算过程中，发现不同的种群数量和迭代次数会产生不一样的目标函数优化曲线，种群数量分别为10、20、30及迭代次数分别为10、30、50的变压器LCC结果见表4。

表4 目标函数优化结果Tab.4 Objective function optimization results

种群数量为10时，不同迭代次数的目标函数优化曲线如图6(a)、(b)、(c)所示。

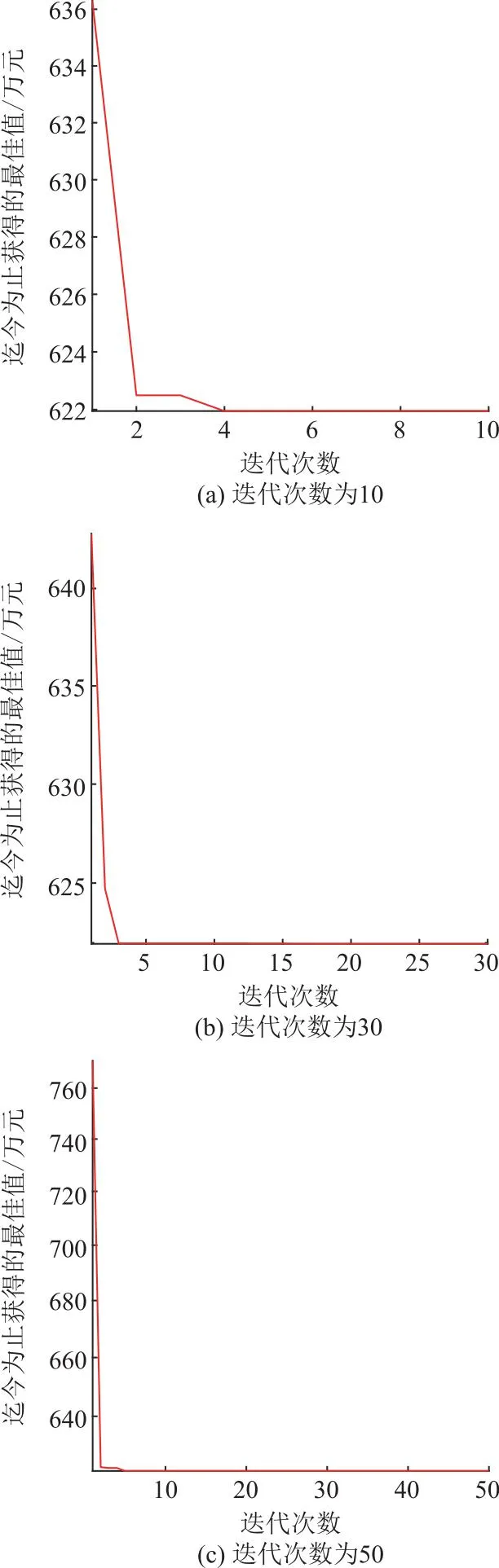
图6 种群数量为10时，不同迭代次数的目标函数优化曲线Fig.6 Optimization curves of the objective function with different numbers of iterations for population size of 10

种群数量为20时，不同迭代次数的目标函数优化曲线如图7(a)、(b)、(c)所示。

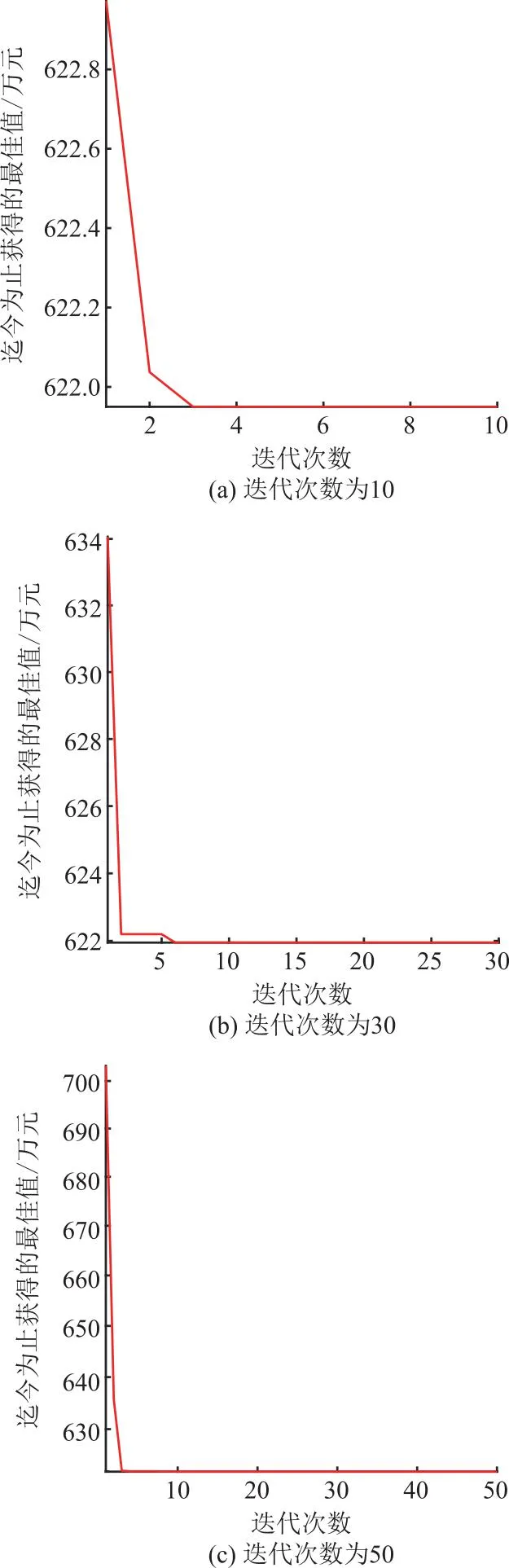
图7 种群数量为20时，不同迭代次数的目标函数优化曲线Fig.7 Optimization curves of the objective function with different numbers of iterations for population size of 20

种群数量为30时，不同迭代次数的目标函数优化曲线如图8(a)、(b)、(c)所示。

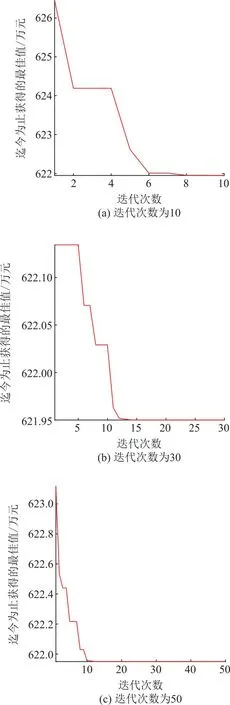
图8 种群数量为30时，不同迭代次数的目标函数优化曲线Fig.8 Optimization curves of the objective function with different numbers of iterations for population size of 30

由图6—8可以看到：①在相同的迭代次数下，种群数目越小，优化曲线越平滑，这是因为种群越小收敛越快，越容易进入局部最优解。相反，种群越大计算收敛越慢，是因为随着种群的扩大，想要在选择中覆盖所有解的概率越来越小，很容易导致计算的无效化，因此一般能采用种群算法的问题规模都不会太大[35]。②在相同的种群数量下，迭代次数越多，优化曲线越平滑。这是因为目标函数在未完全达到稳定并基本收敛时，迭代次数越大，精度越高，获得曲线越平滑[36]。本文所列举的3个不同迭代次数均在合理范围内，因此有以上规律。③当种群数量为10和30时，随着迭代次数的改变，出现最优值的迭代数变化较大；当种群数量为20时，出现最优值的代数维持在一个稳定的水平，变化不大。

因此，种群数量为20、迭代次数为50时的目标函数优化曲线是本算例变压器LCC的最佳优化曲线，最佳优化值为621.949万元。相较于种群数量为10的变压器优化成本，该目标函数优化成本节约近0.1%；相较于种群数量为30的变压器优化成本，该目标函数优化曲线收敛及出现最优值代数更稳定，可以获得更加精准的最佳优化值。

通过选取110 kV变压器的一个案例并对其开展鲸鱼算法优化，可以在较短时间内找到接近最优解的解决方案。对于其他电压等级变压器的优化问题，WOA依旧可以适应不同电压等级以寻找最优解，无论是在电力系统的设计中还是在其他工程领域中，都可以使用WOA来解决与变压器优化相关的问题。总之，WOA具有高效性、灵活性和通用性等优点，使用WOA可以有效地优化不同电压等级的变压器，在实际应用中可以使用WOA来寻找最优的变压器LCC，以降低变压器的成本和提高能源利用效率。

4 结论

a)本文通过对大量电网变压器LCC数据的处理可以得到不同电压等级下变压器LCC波动范围、均值分布特点，并得到规律：随着电压等级的增加，变压器LCC也在提高；较高电压等级的变压器LCC更加集中，波动范围更小，成本数据更加稳定，从长远来看，较高电压等级的变压器能够节省能源和维护成本。相较于之前的研究，本文梳理不同电压等级变压器LCC数据，绘制图表更加直观地表现上述规律，弥补了传统的电压等级对变压器LCC影响的研究的缺失，对实际应用中选择变压器有一定的指导作用。

b)本文基于第1章建立的变压器LCC模型，使用具体算例，选取LCC较低、数据较为稳定的北方某变电站110 kV变压器作为研究对象，仅考虑各部分成本对总成本的影响，计算了变压器从投运到退役的各类成本所占LCC比例，由此得到：C1在投运期内稳定地占据所选110 kV变压器LCC的98%，因此，在选取变压器时，应该重点关注所选变压器的C1，科学规划初期方案，高效管理人员设备，尽可能地减少在采购建设、财务管理、人工培训等方面的支出。相较于之前的研究，本文将其他影响因素设置为定量，将重点聚焦在C1、C2、C3、C4和C5对总成本的影响，揭示了C1对变压器LCC的重要影响，对实际应用过程中帮助企业做出更明智的决策，降低能源消耗和成本有重大意义。

c)种群数量为20、迭代次数为50时的目标函数优化曲线是本算例变压器LCC的最佳优化曲线，最佳优化值为621.949万元。相较于之前的研究，本算例展现了WOA非常强大的竞争力和可利用能力，它的原理也相对直观，便于理解，这有助于更清晰地解释和传达实际应用中的优化结果，可以为变压器LCC优化提供非常好的优化途径，对实际应用中优化变压器LCC提供了可靠的依据和参考。