近海复杂环境下UUV动态路径规划方法研究
2024-04-09张宏瀚王亚博李娟王元慧严浙平
张宏瀚,王亚博,李娟,王元慧,严浙平
(哈尔滨工程大学 智能科学与工程学院, 黑龙江 哈尔滨 150001)
水下无人航行器(unmanned underwater vehicle,UUV)在水下搜救、地形勘探、探测资源等领域有着重要的地位[1],而自主路径规划是UUV的核心技术之一,其决定着UUV执行任务的效率和安全性[2-3]。无人智能系统的路径规划分为全局路径规划和局部动态规划两部分,前者基于不完整地图快速搜寻一条可达任务目标点的可行路径[4-9];后者则是利用智能系统的传感器对周围环境的感知及时避开全局路径上的未知障碍物[10-11]。然而,近海环境下大量礁石、人工建筑物以及航行的渔船等因素致使UUV的航行情况变得异常复杂,对路径规划的要求也相应提高[12]。当UUV停泊港内需执行港外近海任务时,若其具备近海复杂环境下的动态路径规划能力,在抵达任务区域过程中则不需要借助大型渔船及起吊装置,将极大的节省人力物力,对完善UUV功能有着重要的工程意义。
针对动态环境的路径规划问题,Chowdhury等[13]提出了一种PRM-A*算法,该算法将PRM算法和A*算法联合规划路径,解决了路径不平滑以及动态障碍物的避碰问题。赵旭等[14]提出了一种改进的A*算法,此算法将A*算法的搜索区域改为UUV可达的扇形区域,并且在路径拓展阶段以运动学为约束,实现了未知环境的路径规划问题。He等[15]提出了一种改进的蚁群算法,引入虚拟可视化概念克服了蚁群只能在相邻网格行走的限制,使用非线性惩罚机制避免路径出现大的转角。李杨等[16]在遇到动态障碍物时将人工势场法与速度障碍法相结合,根据障碍物的大小以及运动信息使UUV合理避障。
RRT(rapid-exploration random tree)算法由Lavall等[17]提出,被广泛用于解决路径规划问题,但是RRT算法存在拓展盲目性、路径冗余度高、路径不平滑等问题,主要的改进方向有增加算法的导向性和提高的路径可行性[18-20]。刘成菊等[21]提出的RRT改进算法在拓展阶段以一定概率选择目标点,采样的其他点则增加引力分量使其偏向目标点,同时使用路径缓存策略以及动态扩展策略解决动态避碰问题。尹高扬等[22]在节点拓展阶段添加动力学约束、航迹距离约以达到增加路径的可行性以及缩短距离的作用。上述提出的算法在静态环境下效果较好,但是存在计算开销大、不适用于近海环境存在动态障碍物的路径规划问题。
为了解决近海复杂环境下的动态路径规划问题,本文提出一种改进RRT和动态窗口法融合的动态避碰算法AGT-RRT(adaptive guidance target RRT)。首先对RRT算法进行改进以加快全局路径的规划速度,然后在得到的全局路径基础之上,使用自适应子节点选取策略获取DWA(dynamic window approach)算法的子目标点,将难以实现的全局动态任务规划分解成多个简单的动态规划任务,实现动态避碰功能的同时增加DWA算法的导向性。最后,通过仿真验证了算法的有效性。
1 建立UUV模型
近海环境下由于水位较浅,为了简化系统模型,本文只讨论UUV的水平方向运动,即UUV的纵荡、横荡、艏摇3个自由度。
1.1 建立UUV运动学模型
式中:ψ为UUV的艏向角,r、u、v分别为UUV的角速度、横向线速度、纵向线速度,x、y分别为UUV在水平位置坐标。
1.2 建立UUV动力学模型
式中:
其中:m为UUV的自身质量,Xu˙、Yv˙、Nr˙为UUV的附加质量,τ1、τ3为UUV推进器提供的推力以及提供的转向力矩,Jz为转动惯量。
1.3 建立UUV声呐模型
引入文献[23]中提到的Solstice声呐模型,该声呐为多孔径测扫声呐,当障碍物处于声呐的200 m范围内可以被其捕捉到,被捕捉到的障碍物和声呐之间的距离关系如下:
式中:x0、y0分别为UUV在水平位置坐标,x、y分别为障碍物在水平位置坐标,R为声呐有效工作范围。
1.4 建立UUV自身物理约束模型
UUV在运动过程中由于自身性能影响,存在最大速度、转向角的限制:
式中:Vs为速度对(v,r)的约束范围,vmin、vmax为UUV速度v的最大最小值,rmin、rmax为r的最大最小值。
2 全局路径规划算改进
2.1 自适应目标引导策略
本小节介绍为增加随机树生长的方向性设计的自适应目标引导策略。在任务空间V中随机获得一个采样点,首先计算采样点与终点之间的距离d,然后将距离d乘以比例因子p得到一个距离d′,之后将采样点xrand朝着xrand与xgoal的矢量方向移动d′,得到一个新的采样点,其计算公式如下:
这样此算法不仅使拓展的方向偏向xgoal,而且树空间T中更加靠近xgoal的节点被优先被选为拓展点,加快了算法收敛的速度。
比例因子如果设置的过大,在复杂任务环境容易陷入局部极小值(见图1(a)),此时比例因子为0.3,即使多次迭代也不能摆脱。因此本文采用自适应比例因子。在算法开始迭代之前赋予比例因子一个初始值,然后根据每次迭代成功或是失败修改比例因子,以加快收敛速度,防止陷入局部极小值,其计算公式如下:

图1 算法改进前后对比Fig.1 Comparison chart before and after improvement
迭代成功:
迭代失败:
式中:nsuccess、nfail分别为成功迭代次数以及失败迭代次数,α、β、χ、δ分别为权重,p0为比例因子p的初始值。改进后拓展图如图1(b)所示。
2.2 避碰策略
观察算法规划过程发现采样点远大于随机树节点数量,这是由于在拓展阶段发生多次碰撞,为了进一步加快收敛速度,本文采用避碰策略。
当算法发生碰撞时不会直接放弃此条路径而是以朝向的矢量方向为轴线向周围辐射出一个扇形区域,在此扇形区域以一定间隔生成多条路径,如果其中有无碰路径,则按照此方向相应的进行拓展。
在采用转向避碰策略之后如果仍然不能成功拓展则表示此节点大概率陷入局部极小值,为了逃离局部极小值本文采用重选节点避碰策略。在拓展的阶段放弃作为拓展的随机节点,选用之前生成的xrand作为拓展的节点,则使拓展的方向偏离目标点,可以快速逃离局部极小值。
图2中给出了避碰策略的有效性,灰色、洋红色、蓝色曲线分别表示正常拓展、转向避碰策略后拓展、重选节点避碰策略后的路径。从图中可以发现,随机树在发生碰撞之后可以根据节点所处的不同情况选取不同的策略,在随机树朝向目标点生长时如果陷入局部极小值,可以使用设计的策略快速逃离,达到了设计的目的。
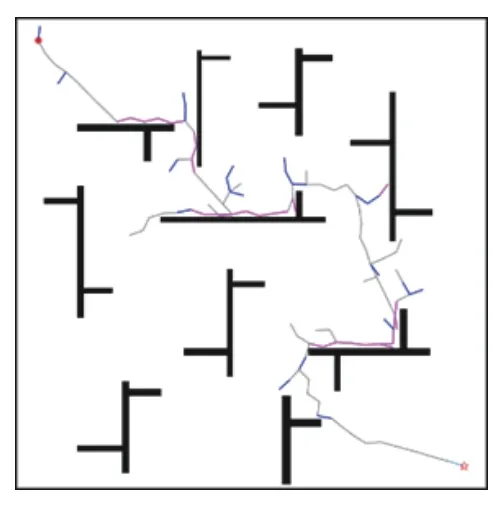
图2 避障策略仿真Fig.2 Simulation diagram of obstacle avoidance strategy
3 局部避碰算法设计
本文采用DWA算法实现局部路径规划,但是DWA算法仅能在窗口大小的范围内规划路径,极易陷入局部最小值。为了解决这个问题,本文采用自适应子节点选取策略和重规划策略。
3.1 DWA模型设计
1) DWA规划UUV下一时刻状态方程如下:
式中:x=[xyψvr]T,V为速度对[vr] 。
2)制动距离计算,当制动距离Ddis大于UUV与障碍物的距离则舍弃相应的路径,公式如下:
其中amax为UUV的最大加速度。
3)评价函数计算,评价函数主要由艏向角得分、安全距离得分以及速度得分3部分构成。为了防止不同评价体系单差异带来的异常,对3种评价体系归一化处理,具体公式如下:
其中Ei为每条轨迹的参数。最后可得评价函数如下:
其中:e为评价函数得分,a、b、c分别为艏向角的分系数、安全距离的分系数、速度得分系数。
3.2 自适应子节点选取策略
在未知路径弯曲度时,固定距离子节点易导致DWA算法陷入局部最小值,因此本文提出自适应子节点选取策略。首先,初始长度dinit,在全局路径上选取距离当前位置一个初始长度的子节点xchild,之后计算当前位置和子节点在全局路径上的距离d1与当前位置到子节点的直线距离d2的比值k,如果比值大于设置的阈值κ表示全局规划的路径较为曲折,则缩短子节点的选取距离,直至小于设置的阈值;如果比值小于设置的阈值κ则表示路径较为平滑,则增加子节点的选取距离,直至大于设置的阈值。
3.3 重规划策略
全局路径规划是基于不完整地图信息规划的路径,在实际环境中可能会出现新的障碍物,当障碍物较小使用DWA即可避过障碍物,但是当障碍物过大,DWA算法可能会陷入局部极小值导致UUV无法通行。因此本文针对这种情况采用重规划策略,当DWA算法陷入局部极小值时,则返回主程序中,把雷达扫描到的障碍物加入到地图之中,然后以当前位置为起点重新规划全局路径,之后再按照之前设计的方案进行规划路径。
4 仿真与分析
4.1 AGT-RRT算法仿真验证
AGT-RRT算法在运行时首先初始化随机树空间,初始化自适应比例因子p0为0.32,初始化计数器nsuccess、nfail为0,转向避碰策略角度α为30°。在任务空间获得采样点xrand,执行目标引导策略获得采样点。若拓展成功则将其加入随机树空间;失败则执行转向避碰策略获得采样点xnew,若其成功拓展则将其加入随机树空间;失败则执行重选节点策略,采用xrand作为拓展的节点,若其成功拓展则加入随机树空间,失败则返回第一步在任务空间重新获得采样点。
本文设计了map1和map2验证AGT-RRT算法的可行性。将经典RRT算法、文献[11]中提出的AWA_RRT重算法、RRT-Connect算法与本文提出的算法作对比。控制每种算法的参数一致,步长均为30,AWA-RRT算法权重的初始值为0.5,AGT-RRT算法比例因子初始值为0.32,map1和map2的大小均为1 000×1 000,起止点为(50,50),目标点为(950,950)。由于每次规划所需时间过少,为避免偶然性和便于对比分析,表1、2为1 000次规划的总时间成本,路径成本以及节点数量取1 000次规划的平均值。

表1 map1 4种算法仿真数据Table 1 Map1 simulation data of four algorithms
图3给出了4种算法在两种环境下的仿真情况。map1环境较为简单不存在局部极小值。本文算法可以使用转向避障策略顺利躲避障碍物。每次成功的拓展都会提高自适应目标引导策略比例因子的值,使得下一个采样点更加接近目标点,加快了算法的收敛速度。对比观察map1中路径生成过程发现AGT-RRT算法拓展方向具有较好的引导性,基本没有冗余节点,达到了设计的目的。

图3 4种算法在不同环境的仿真图Fig.3 Simulation diagrams of four algorithms in different environments
在存在局部极小值的map2中,对比算法增加许多无效拓展,而本文的算法可使用重选节点避碰策略绕过局部极小值。使用重选节点避碰策略表示环境较为复杂,则会降低自适应目标引导策略比例因子的值,以增强探索能力。map2中的AGT-RRT算法在应对局部极小值,产生的无效拓展较少,证明了设计的有效性。
对比表1和表2中数据发现,AGT-RRT算法在map1中时间成本相较于RRT、AWA-RRT、RRT-Connect算法分别减少94.1%、91.3%、72%,路径成本也分别优化了18.1%、4.9%、15%。在环境更为复杂的map2中,时间成本分别减少79%、66.4%、40.8%,路径成本相较于RRT算法和RRTConnect算法分别减少4.2%、5.4%,但是相较于AWA-RRT算法路径成本增加了14.3%,节点数量减少78%。结合map2仿真环境和图3中路径观察可知,这是由于本文算法在遇到障碍物优先执行转向避障策略,加快算法的收敛速度所致。时间成本的减少,增加的路径成本在可接受的范围。观察图4和图5箱线图中的数据可以发现,所提出的算法有较少的离散点,这表明其鲁棒性优于其他的3种算法,在不同的环境中有更强的适应能力,达到了设计的目的。

表2 map2 4种算法实验结果Table 2 Map1 simulation data of four algorithms
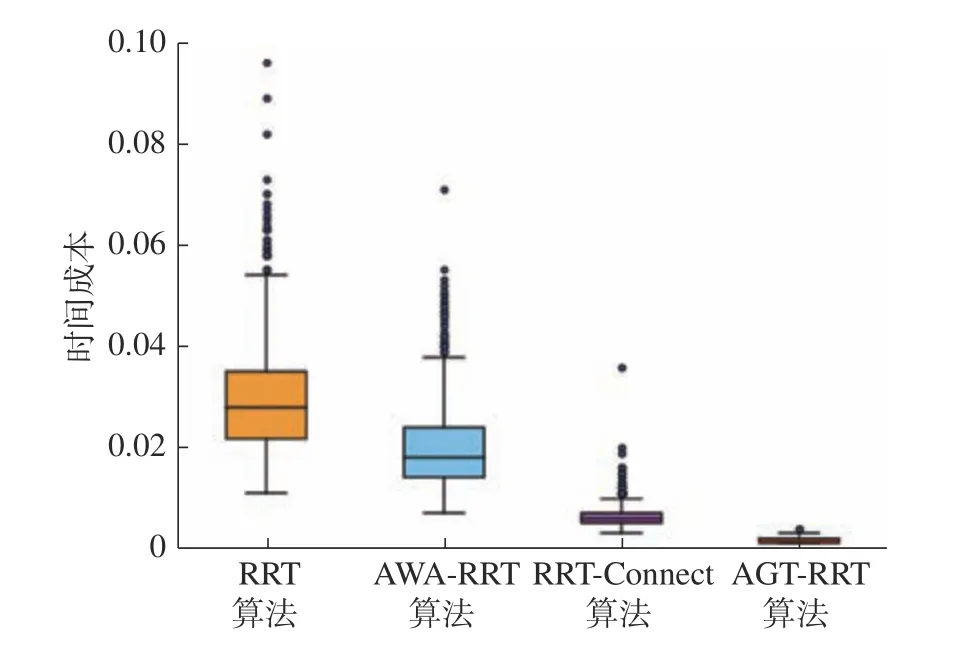
图4 map1 4种算法时间成本箱线图Fig.4 Map1 four algorithms time cost boxplot
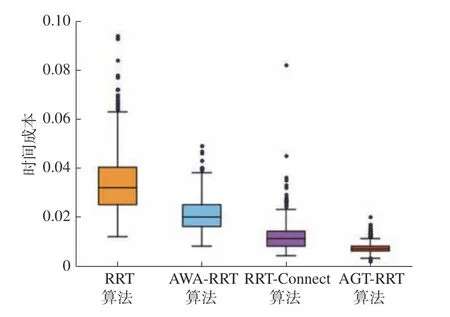
图5 map2 4种算法时间成本箱线图Fig.5 Map2 four algorithms time cost boxplot
使用AGT-RRT算法生成的路径距离障碍物太近,转向次数较多,不满足实际路径规划的需求。本文将障碍物膨胀化保证路径远离障碍物,同时去除冗余节点减少路径的转向次数,使生成的路径更为平滑,处理后的路径如图6所示。

图6 去除冗余节点路径(蓝色)Fig.6 Remove redundant node path (blue)
4.2 动态路径规划仿真分析
为证明本文所设计算法的有效性,使用文献[24]中所提出算法作对比仿真实验。动态路径规划仿真结果如图7所示,大小为500 m×500 m。固定变量,两种算法均采用图7中蓝色折线作为全局路径。二者算法参数见表3,其中d为对比算法特有的偏离函数权重,UUV性能参数见表4。路径的初始位置为(50,50),终点为(470,470),初始方向角为0。

表3 DWA算法评价函数权重Table 3 Weights of DWA algorithms evaluation function

表4 UUV性能参数表Table 4 UUV performance parameters

图7 动态路径规划仿真结果Fig.7 Simulation result of dynamic path planning
图7中洋红色曲线为动态规划的路径,其中图7(a)和图7(b)为map3和map4的仿真结果,左图为对比算法,右图为本文所设计算法。本文算法首先执行自适应子节点选取策略,根据路径的曲折程度选取DWA算法的子目标点。自适应子节点选取策略将完整的动态规划任务分解为多个子任务分别进行规划,从而降低全局路径的曲折度对动态规划的影响。
为增加仿真结果的可靠性,分别对二者进行10次仿真实验,取平均值作为结果,具体数值见表5。从图7(a)中可以看出二者均可以较好的参考全局路径执行动态路径规划任务,通过计算发现,二者平局路径长度相差只有1%,但是本文所提出算法规划的路径速度提升了10.4%,具有较大的速度提升,加快了任务的执行速度。
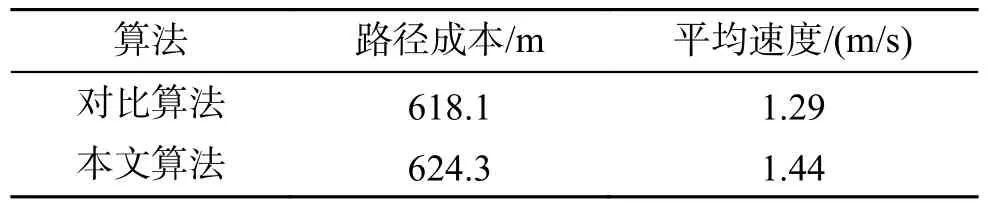
表5 地图3仿真数据Table 5 Map 3 simulation data
在map4中,本文所设计的算法借助自适应子节点选取策略可以较好地利用全局路径进行动态路径规划,而对比算法丢失了全局路径信息,超出任务边界无法抵达目标点。map4 比map3中全局路径转折角大,任务目标点与航行器当前艏向角相差过大,而UUV为大惯性体转向速度较慢,导致对比算法脱离全局路径,造成最优评价路径更加偏向任务目标点,使得规划路径超出任务范围,无法完成近海复杂环境中的UUV出港任务,证明了本文算法的优越性。
4.3 出港任务仿真分析
仿真实验任务为航行器自主动态规划出港路径,以抵达港外任务区域。地图实际大小为400 m×400 m,像素大小为1 200×1 200,比例为1∶3。
在仿真实验中,本文采用Bluefin-9型UUV参数[25],见表4。在使用AGT-RRT规划全局路径时以UUV最大航速(3 m/s)为一个步长,DWA规划路径时取最大航行速度为3 m/s。首先,AGTRRT算法规划出一条全局路径,虽然在狭小空间存在一些无效拓展,但是使用避障策略可轻易摆脱局部极小值,达到设计目的,之后去除初步规划全局路径的冗余节点。获得全局路径之后执行动态路径规划任务,使用自适应子节点选取策略在全局路径上不断选取子节点作为DWA算法的目标点,将复杂的路径规划任务分解成多个简单的动态路径规划任务。之后DWA算法按照顺序依次以生成的子目标点作为每阶段的目标点执行动态路径规划任务,最后获得出一条符合运动学约束的路径。
任务执行过程中UUV速度每秒变化曲线以及角速度每秒变化曲线如图8和图9所示,可以发现,速度出现的几次较大变化是由于每当DWA算法抵达目标点就会逐渐降低自身速度,保证UUV可以停止在目标点,最大速度变化率为0.6 m/s2,没有超过最大加速度;角速度出现较大变化是由于路径出现较大转角,最大角速度变化率为0.5 rad/s2,没有超过最大角加速度的范围。总路径长度为421 m,平均速度为1.5 m/s,可以较快完成出港任务。速度以及角速度的变化在切换子目标点以及在较为急促转弯时变化较为剧烈,其余规划时间变化均较为平缓,符合UUV的运动特性,达到设计的要求。

图8 速度变化率曲线Fig.8 Velocity change rate curve

图9 角速度变化率曲线Fig.9 Angular velocity change rate curve
5 结束语
为了提高近海环境特别是港口环境中UUV自主路径规划的安全性、快速性和动态避障能力,本文结合全局和局部路径规划设计了一种算法。首先,分析RRT算法存在的不足提出一种AGT-RRT算法。针对RRT的拓展盲目问题提出了自适应目标引导策略,同时引入转向机制提高RRT算法的采样成功率,进一步提高全局路径规划的效率,最后对比仿真实验验证了算法的有效性。针对DWA算法难以在较为复杂的环境实现动态规划任务,采用自适应子节点选取策略获取DWA算法的子目标点,将难以实现的全局动态任务规划分解为多个简单的动态规划任务,从而实现复杂环境下的动态路径规划,仿真实验验证了算法的有效性和实用性。然而本文算法只能利用当前位置及下一个子目标点的信息,无法做到全局信息的利用,导致有些地方路径较长,速度变化不平滑,对这些问题的处理将是今后的研究工作。
