三维荧光光谱结合IGOA-SVM分类鉴别油类污染物

程朋飞, 朱燕萍, 潘金燕, 崔传金, 张 怡

1. 徐州工程学院电气与控制工程学院, 江苏 徐州 221018

2. 华北理工大学电气工程学院, 河北 唐山 063210

引 言

石油是一种由多种含烃分子组成的难以降解的复杂有机污染物, 溢油污染会以多种形式对人类生产生活、 生态环境和生物多样性带来难以挽回的危害[1-2]。 特别是其中所含的多环芳烃, 会严重损害呼吸系统、 神经系统和肾脏等, 甚至会有很强的致癌性[3]。 提高溢油检测的精确度和可靠性对选择清理策略以及评估潜在的环境和生态影响具有重要意义。 三维荧光光谱分析以其灵敏度高、 分析速度快、 选择性好和可实时检测等优势在溢油检测领域迅速占领一席之地[4]。

支持向量机(SVM)是在风险最小化和统计学VC维理论基础上形成的一种具有自主学习能力的监督型机器学习算法, 通过超平面的选择和高低维转换思想巧妙地简化了计算[5], 在非线性、 高维及小样本问题分析中具有一定的优势。 目前, 基于群智能优化算法改进的SVM广泛应用于样本的分类识别领域中。 王书涛等[6]实现了三维荧光光谱结合遗传算法优化支持向量机(GA-SVM)对三种不同组合多环芳烃的分类鉴别。 Huang等[7]分别将三种优化的SVM方法, 包括粒子群优化算法(PSO)、 遗传算法(GA)、 和网络搜索算法(GS)应用于铁路危险货物运输系统(RDGTS)的风险识别中。 Zhou等[8]将优化的支持向量机(BSO-SVM)算法应用于局放超声信号的模式识别中。 结果表明, 相对于GA-SVM和PSO-SVM算法, BSO-SVM算法具有较高的识别精度和较快的收敛速度。

蚱蜢优化算法(GOA)改进了粒子群优化算法忽略种群中其他个体影响的缺陷, 但该算法在解决复杂问题时存在精确度的稳定性不佳、 易陷入局部最优和收敛速度慢的缺陷[9]。 鉴于此, 国内外学者采取了一系列的措施对其进行改进。 宋长新等[10]提出了一种基于差分进化改进的蝗虫优化算法, 在收敛速度和精度上均有一定的改善。 王生生等[11]采用对立点搜索算法、 正余弦搜索算法、 Lévy飞行的随机扰动机制和非线性收敛相结合的方式优化GOA, 将其应用于电动汽车充换电站调度中, 经优化后的IGOA在运行效率、 全局搜索能力和收敛速度等方面均得到有效的提升。 Arrif等[12]提出的混合GA-GOA算法可以经济有效地优化定日镜场布局设计, 减少其土地足迹。

本文采用改进蚱蜢优化算法(IGOA)结合SVM的模型实现三种石油混合物的分类鉴别。 首先, 采用混沌初始化代替原来的随机初始化方式, 加强初始种群多样性。 其次, 采用精英优化策略提高算法跳出局部最优的能力。 最后, 采用差分进化策略提高算法收敛速度, 在石油类污染物的定性分析上提出了新的方法。

1 理论部分

1.1 支持向量机

SVM通过引入核函数将线性不可分的样本映射到高维空间, 通过在高维空间寻找最优超平面实现样本线性分类。 同时, 为简化高维空间的计算难度, 将计算转化到低维空间中, 有效提高运算速度。 核函数g和惩罚因子C是支持向量机中最为重要的两个参数[13], 核函数是将数据从低维空间映射到高维空间的映射方式, 惩罚因子是指对分类错误的重视程度和容忍范围。 设定合适的g和C数值能有效提高支持向量机回归预测的精度。

假设空间中的各样本点为(xi,yi),i∈[1,N], 其中xi为第i个样本,yi为第i个样本的标记类别,yi取+1或-1, 分别代表所测样本为正样本和负样本。

优化目标函数和约束条件为

(1)

(2)

决策函数为

f(x)=sign(ω*Tx+b*)

(3)

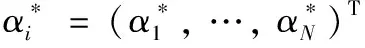
本文采用径向基(RBF)核函数, 该核函数因其映射维度广, 需要参数少, 运算简单, 在一般的小特征样本处理中应用最广, 如式(4)

(4)

1.2 蚱蜢优化算法GOA

蚱蜢优化算法(grasshopper optimization algorithm, GOA)是一种新型的元启发式算法, 由Mirjalili等于2017年提出。 该算法受幼虫和成年蝗虫大范围移动与寻找食物源的聚集行为启发, 具有操作参数少, 公式简单等特点[14-15]。

GOA算法分为探索和开采两部分, 幼虫时期的蚱蜢运动缓慢, 只能进行短距离的捕食, 恰好对应于算法的开采过程。 成年期的蚱蜢种群发育成熟, 成群聚集且快速移动探索远距离的食物, 对应算法的探索过程。 蝗虫优化算法优于粒子群算法的关键点是新位置的计算不仅依赖于当前位置、 全局最优位置, 还受种群中其他个体位置的影响, 通过种群个体间相互吸引及排斥的社会活动, 朝着全局最优值不断靠近。

在D维空间中, 假设蚱蜢种群总体为X={xi},i∈[1,N], 蚱蜢算法位置更新的数学模型为

(5)

由式(5)可得, 新种群位置更新公式为

(6)

式(6)中,ud和ld分别为D维空间搜索域的上限和下限;T当前算法搜索到的最优位置,c为线性递减参数, 其计算公式为

(7)

式(7)中,cmax为参数的最大值,cmin为最小值,t为当前迭代次数,L为算法最大迭代次数。

1.3 改进蚱蜢优化算法IGOA

1.3.1 混沌初始化

原始GOA算法中, 蚱蜢位置更新采用的是随机初始化方式, 如式(8)所示

Xid=ld+rand(ud-ld),Xid∈[0, 1]

(8)

式(8)中,Xid为个体Xi在D维空间中坐标点的随机数, 这种随机初始化方式分布不均匀, 易陷入局部最优, 影响算法的收敛速度, 采用混沌序列能很大程度上保留最初种群的多样性[16]。

在D维搜索域中, 将每个蚱蜢的位置看成一个D维矢量, 即Y1={Y1i},i∈[1,D]且Y1i∈(0, 1), 采用Logistic函数将Yi映射到混沌空间中, 将得到的N个混沌矢量Y1,Y2, …,YN变换到搜索域中, 即可得到初始化后的蚱蜢种群。 如式(9)所示

(9)

1.3.2 精英反向学习优化

(10)

1.3.3 差分进化优化

差分进化算法(differential evolution, DE)是在遗传算法基础上进行优化的启发式算法, 相对遗传算法相同点都是由变异、 交叉、 选择三部分组成, 不同点是遗传算法需要进行二进制编码, DE中的子代向量是由父代差分交叉生成, 且后续父代会与新形成的子代个体共同参与选择, 大大提高了算法的收敛速度[17]。 本文差分进化的父代个体Xbest, j是精英优化后的最优个体, 具有一定跳出局部最优的能力, 其优化公式为

(11)

式(11)中,Vi, j为变异个体向量;Xbest, j为精英反向学习后选出的最优个体的第j维;n和m均为1到N范围内且互不相同的随机整数;F为缩放因子。CR∈[0, 1]为交叉概率;f为适应度函数。 差分进化将交叉变异后适应度值较低的值筛选出来代替精英反向最优解, 使得算法的优化结果更加靠近全局最优解。 改进蚱蜢优化算法具体流程如图1所示。

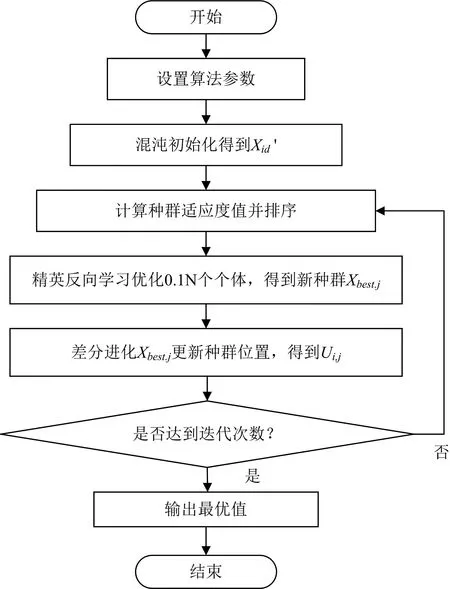
图1 改进蚱蜢优化算法流程图

2 实验部分

实验采用日本Hitachi公司的F-7000荧光光谱仪对油类污染物的荧光特性进行分析。 激发和发射波长的扫描范围分别设置为250～400和270～450 nm, 设置激发波长超前发射波长20 nm以防止瑞利散射的干扰。 设置激发和发射扫描步长均为5 nm, 狭缝宽度均为2.5 nm, 为提高扫描数据的准确性, 取3次扫描数据的平均值作为采样数据。

从市场采购标准0#柴油、 95#汽油和煤油作为待测油类污染物, 用精度为0.1 mg的电子天平称取28.84 g十二烷基硫酸钠固体粉末于1 000 mL去离子水中, 配制成0.1 mol·L-1SDS胶束溶液作为溶剂, 分别称取0.1 g三种油于100 mL容量瓶中, 加入溶剂定容得到三种油的浓度为1 000 μg·mL-1的标准溶液, 将三种油按一定比例混合后定容, 配制成20个不同浓度的0#柴油和95#汽油的混合溶液样本, 18个不同浓度的0#柴油和煤油的混合样本和20个不同浓度的三种油的混合样本。

2.1 单组分样本光谱分析

如图2所示为经去散射等预处理后得到的三种油各自的荧光光谱图和等高线图, 由图2(a)和(b)可知, 0#柴油有两个荧光峰, 峰值最强的主峰位置为λex/λem=280/330nm, 次峰位置为λex/λem=270/305 nm。 图2(c)和(d)中95#汽油有两个荧光峰, 位置分别为λex/λem=275/295 nm,λex/λem=280/335 nm。 图2(e)和(f)中煤油最佳荧光峰值位置为λex/λem=270/290 nm。 从图2(d)可以看出, 95#汽油的较强激发光谱范围为260～290 nm, 发射波长范围为285～345 nm, 与0#柴油和煤油的荧光光谱出现了严重的重叠, 仅通过直观的查看荧光光谱图无法准确辨别各样本属性。

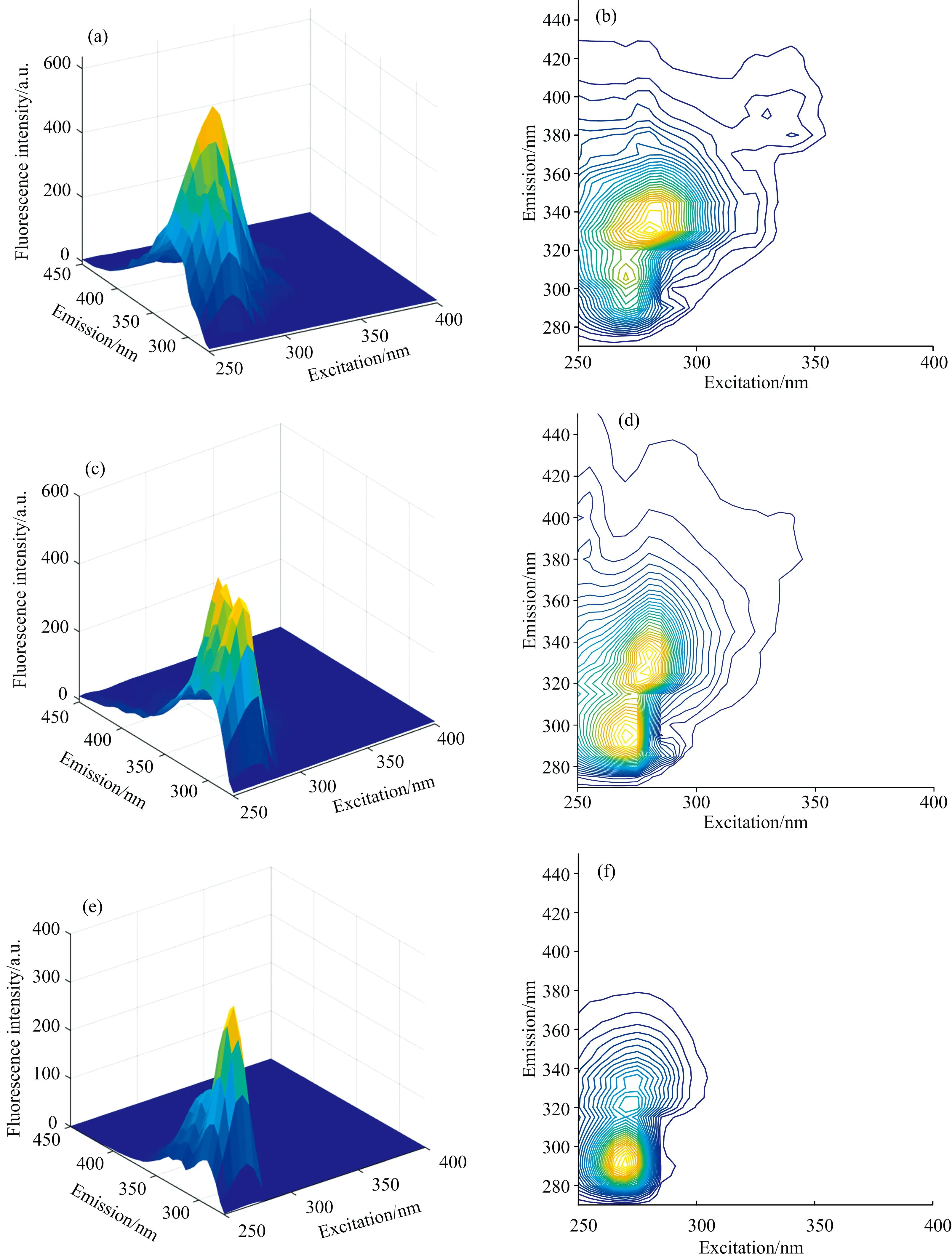
图2 0#柴油、 95#汽油和煤油溶液的荧光光谱和等高线图

2.2 混合样本光谱分析

图3(a)、 (b)为0#柴油/95#汽油, 浓度分别为150/120 μg·mL-1的混合样本测得的荧光光谱图和等高线图, 图3(c)、 (d)为0#柴油/煤油, 浓度分别为120/200 μg·mL-1的混合样本测得的荧光光谱图和等高线图, 图3(e)、 (f)为0#柴油/95#汽油/煤油, 浓度分别为250/150/120 μg·mL-1的混合样本测得的荧光光谱图和等高线图, 由图3可知, 三个样本荧光特性均有两个荧光峰, 且激发波长和发射波长荧光最强范围均为λex∈[265, 275],λem∈[285, 345], 荧光峰位置与单组分95#汽油荧光峰位置相似, 溶液经混合后荧光强度也明显降低, 仅依靠直观观察无法准确识别各成分, 因此, 采用IGOA结合SVM方法为油类污染物的准确识别提供了一种有效的方法。

图3 三种混合样本的荧光光谱图和等高线图

3 结果与讨论

3.1 传统SVM分类分析

实验共设计58个样本, 其中0#柴油和95#汽油混合样本20个(A1—A10为训练样本, A11—A20为测试样本)。 0#柴油和煤油混合样本18个(B1—B9为训练样本, B10—B18为测试样本)。 0#柴油、 95#汽油和煤油的三组分混合样本20个(C1—C10为训练样本, C11—C20为测试样本)。 为避免荧光峰值区域外其他区域的干扰, 选取荧光峰值处对应激发波长为270 nm处的荧光数据作为荧光特征值进行训练。

设置SVM的惩罚参数c=100, 核参数g=0.1, 分类预测结果如图4所示, 由图4(a)中混淆矩阵可知, 0#柴油和95#汽油混合样本的分类准确率为100%, 0#柴油和煤油的混合样本分类准确率为77.8%, 三种油混合样本分类准确率为90%。 图4(b)所示, 有两个0#柴油和煤油混合样本被错分为0#柴油和95#汽油样本, 有一个三组分混合样本被错分为0#柴油和95#汽油样本, 最佳适应度为89.67%, 共有3个样本被错误分类, 分类识别准确率为91.18%。 可知仅靠SVM不能达到很好的分类效果。

图4 传统SVM算法样本分类分析

3.2 不同SVM优化算法对比分析

IGOA、 GOA、 PSO和GA四种SVM优化算法的适应度曲线如图5所示, 设置IGOA算法的参数, 种群数量N=20, 算法最大迭代次数L=100, 线性递减参数cmax=1,cmin=0.000 04, 缩放因子F=0.9, 交叉概率CR=0.5。 由图5可以看出, IGOA在迭代到第2代就达到了最佳适应度值并保持稳定, 平均适应度值在第3代保持稳定且与最佳适应度紧密贴合。 GOA在迭代到第8代达到最佳适应度且保持不变, 其平均适应度曲线在37代前一直保持连续震荡, 37代后保持稳定并与最佳适应度曲线一致。 PSO最佳适应度曲线在第4代达到稳定, 收敛速度介于IGOA和GOA之间, 但是平均适应度曲线和最佳适应度曲线之间的差值较大。 相比于GOA和PSO, GA优化算法最佳适应度曲线收敛较慢, GA算法最佳适应度曲线和平均适应度曲线均处于缓慢收敛状态, 最佳适应度曲线收敛过程分为三个阶段, 在第12代后保持稳定, 但平均适应度一直保持震荡状态。 经改进蚱蜢优化算法优化后的IGOA最佳适应度可达到100%, GOA的最佳适应度为97.06%, PSO和GA的最佳适应度均为94.12%。

图5 IGOA、 GOA、 PSO和GA适应度变化曲线

将通过四种优化算法得到的参数c和g带入SVM中分类识别, 图6为优化算法的样本分类结果图, 图6(a)为IGOA的样本分类结果图, 分类准确率可达到100%。 图6(b)为GOA的样本分类结果图, 29个样本中有1个样本被划分错误, 分类准确率为96.55%。 图6(c)和(d)分别为PSO和GA的样本分类结果图, 两种SVM优化算法的分类结果均有两个样本被划分错误, 分类准确率均为93.10%。

图6 IGOA、 GOA、 PSO和GA样本分类结果

通过对比可知, 与传统SVM分类模型相比, 四种SVM优化算法在最终识别准确率上均有所提高, 但是, 经改进后的IGOA在收敛速度、 稳定性和跳出局部最优能力上均优于GOA、 PSO和GA, 能够更加精准、 快速地识别不同样本。

4 结 论

利用三维荧光光谱检测技术分别检测0#柴油、 95#汽油和煤油三种矿物油标准溶液和设计的三种混合溶液样本的光谱数据, 对光谱数据预处理后得到对应的荧光光谱图和等高线图, 通过观察发现在荧光峰波长位置处光谱存在严重重叠现象, 仅用此方法无法准确判定样本类型。 采用传统SVM对样本类型定性分析, 最佳适应度和分类准确率仅达到89.67%和91.18%, 仍然无法准确识别。 采用本文设计的混沌初始化、 精英优化算法结合差分进化算法优化SVM的方式与常用的GOA-SVM、 PSO-SVM和GA-SVM相比, 其在逼近最优值的收敛速度、 收敛过程的稳定性和跳出局部最优的能力均得到了提高, 为提高油类污染物的识别效率提供了一种有效的方法。