一种自适应的三维荧光光谱去散射方法
2024-04-08伍卓慧黄冰佳李学勤王晓萍
伍卓慧, 黄冰佳, 李学勤, 王晓萍
1. 浙江大学海洋学院, 浙江 舟山 316021
2. 浙江大学海南研究院, 海南 三亚 572025
3. 海洋感知技术与装备教育部工程研究中心, 浙江 舟山 316021
引 言
三维荧光光谱检测技术是一种可以同时描绘荧光强度与发射波长和激发波长变化关系的光谱技术。 因为该方法具有选择性好、 信息量大、 灵敏度高和无需对样品进行复杂的前处理工作等优点, 所以被广泛应用于食品[1]、 医疗[2]、 化工[3]和环境[4-5]等领域。
然而, 在三维荧光光谱数据中总是会夹杂着瑞利散射和拉曼散射, 如图1所示。 这两种散射是物质的固有光学特性, 但不符合三线性原则, 散射峰的形状和位置会随激发波长的变化而变化。 并且瑞利散射峰的荧光强度通常要高于样品自身, 会干扰甚至覆盖部分样品的荧光信号, 致使样品本身特征难以表达。 因此往往需要在数据处理前期, 对瑞利散射和拉曼散射进行校正处理。 在以往研究中, 常用的方法有: 空白扣除法[6-7]、 置零法[8]和Delaunay三角形内插值法[9-10]等。 空白扣除法即为直接用所得物质的三维荧光光谱减去溶剂的三维荧光光谱, 该方法操作简单, 但是对于低浓度样品往往存在散射区域去除不完全的缺点。 而置零法则为直接将散射区域内的数据进行替换, 将其设置为零, 此方法虽然简单易行, 但是容易造成有效数据丢失。 Delaunay三角形内插值法, 即用插值所得数据代替散射区域内的原始数据。 既去除了散射干扰, 又尽可能地保留了原始数据特征, 是一种现阶段应用最多且十分有效的去散射算法。 但该方法存在需要定义许多最佳设置不明显的超参数的阻碍, 并且当光谱严重重叠时其适应性较差。 同时不难发现, 现阶段许多算法皆致力于将散射区域内的数值替换为与三维荧光光谱剩余部分数据一致的新数据, 因此常采用二维插值算法。 但研究表明, 它较为复杂, 容易导致过拟合现象发生[11], 而一维插值能够较好地避免这种现象。
因此本文将对单个发射光谱进行研究, 提出了一种自适应的三维荧光光谱去散射方法。 该方法基于一维插值, 综合考虑散射峰和物质峰的荧光强度与重叠程度, 将光谱共分为五类情况对应三种插值算法分别进行散射校正处理。 去除散射后的三维荧光光谱图, 较好的保留了光谱的原始特征, 证明了此方法校正散射干扰的有效性。 同时, 模拟突发水质污染实验表明, 本文方法在提高荧光数据处理的适应性和准确性方面具有潜力。
1 实验部分
1.1 仪器
本实验采用由日本日立公司生产的F-4600 FL荧光分光光度计测定样品的三维荧光光谱数据。 设置发射波长区间为200~700 nm, 步长为5 nm。 激发波长区间为200~600 nm, 步长也为5 nm。 设置仪器的激发与发射狭缝宽度均为10 nm, PMT电压设置为400 V, 扫描速度定为30 000 nm·min-1。 所有计算均使用美国MathWorks公司出品的MATLAB R2021a进行。 利用drEEM工具箱(http://www.models.life.ku.dk/drEEM)构建PARAFAC模型[12]。
1.2 样本
在本研究中, 我们选择了河北沿程生物科技有限公司的酪氨酸、 南通飞宇生物科技有限公司的黄腐酸、 上海摩楷生物科技有限公司的萘乙酸和上海源叶生物科技有限公司的罗丹明B四种典型的化学物质进行实验。 将酪氨酸、 萘乙酸和罗丹明B的浓度梯度均设置为: 20、 40、 60、 80和100 μg·L-1。 将黄腐酸的浓度梯度设置为: 1、 3、 5、 7和9 mg·L-1。 每种化学品均用Millipore公司的Milli-Q水净化系统的去离子水作溶剂配制而成, 各得五个样品。
模拟突发污染水样, 通过自来水与罗丹明B配制而成。 自来水取自浙江大学舟山校区海科楼。 通过控制水流流速, 每5 min取样一次, 共取样30个样本。 为防止非必要性误差的产生, 每个样品均扫描三次三维荧光光谱, 取平均值作为样品最终的三维荧光光谱进行数据分析。
1.3 去除拉曼散射与背景干扰
在三维荧光光谱中, 拉曼散射可近似由水分子与激发光光子相互作用发生能级跃迁而产生, 影响因素较为单一[13]。 且考虑到测试仪器本身的背景噪声也会对实验效果造成影响。 因此我们需要测量每次实验中溶剂的三维荧光光谱, 本实验的溶剂均为去离子水, 将其作为背景基线。 采用原始光谱数据减去背景基线的校正方法, 也称为空白扣除法, 达到校正拉曼散射和背景干扰的目的。
1.4 去除瑞利散射
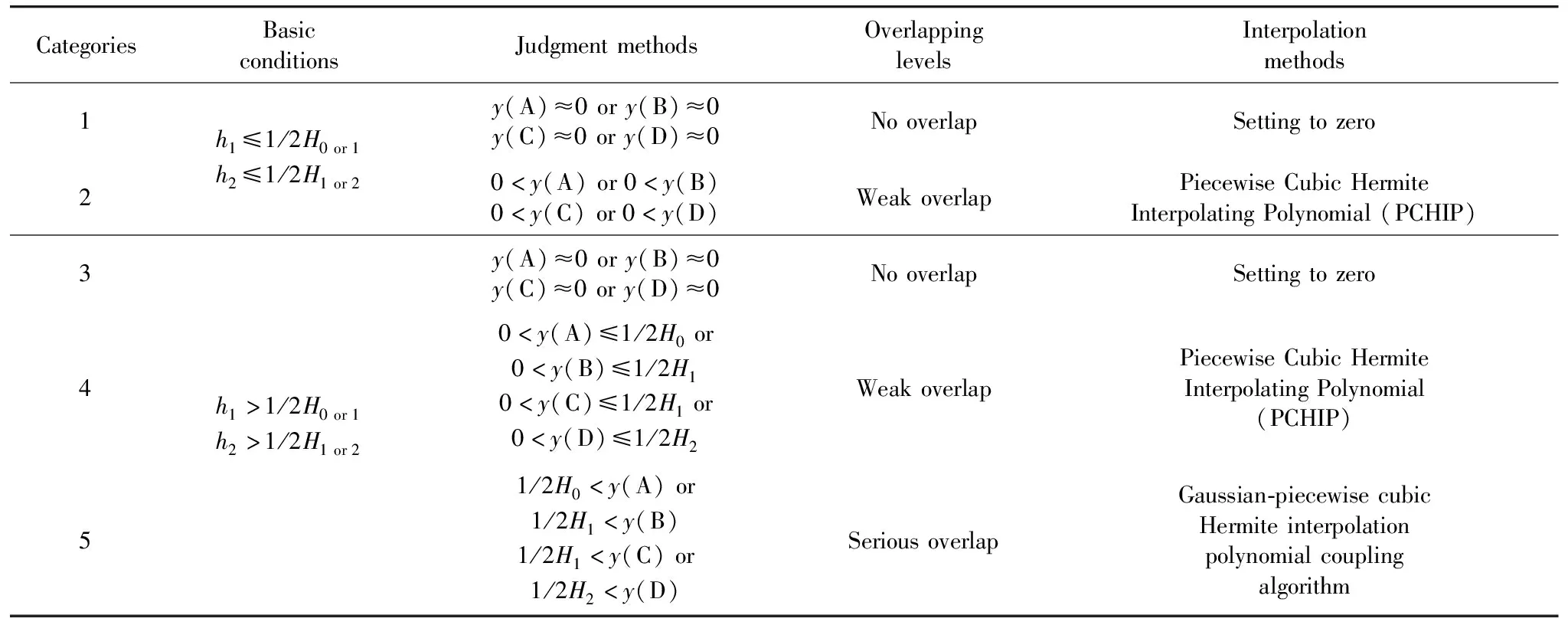
而瑞利散射的产生机理相对于拉曼散射而言要复杂很多。 瑞利散射是由光子与溶解气体、 悬浮颗粒和可溶分子等碰撞而产生的, 影响因素颇多。 因此对于部分样品, 特别是低浓度样品而言, 仅采用空白扣除法往往难以对其达到很好的校正效果。 针对已完成拉曼散射校正的三维荧光光谱数据, 本文将从散射峰与物质峰的荧光强度和重叠程度两方面考虑, 将光谱分为五类情况对应三种重叠等级, 采用一种自适应的散射去除方法对其进行校正。 首先, 对这一节中将出现的参数进行定义与解释说明, 如表1所示。 需要注意的是, 当散射区域与物质峰因重叠过度而致使物质区域没有峰值时, 物质区域峰值即定义为其最大值, 且瑞利散射近似于一个中心在激发波长处的高斯函数[14]。

表1 定义参数与解释说明
然后对即将应用到的三种算法进行简要介绍。 置零法即为用零替换已有数据。 Hermite插值, 也称为具有节点的导数值约束的插值。 因为其严苛的算法要求, 既能保证数据的强关联性又能使所得曲线相对光滑, 在插值领域应用广泛。 然而直接使用Hermite插值得到的多项式往往次数较高, 也存在着龙格现象。 因此在本研究中, 我们采用了分段三次Hermite插值多项式(piecewise cubic hermite interpolating polynomial, PCHIP)以防止过拟合。 高斯拟合即为用高斯函数对已经存在的数据点进行函数拟合逼近。
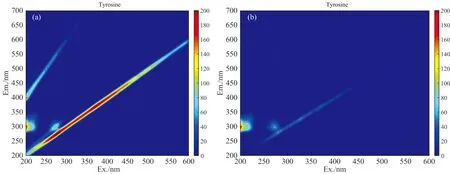
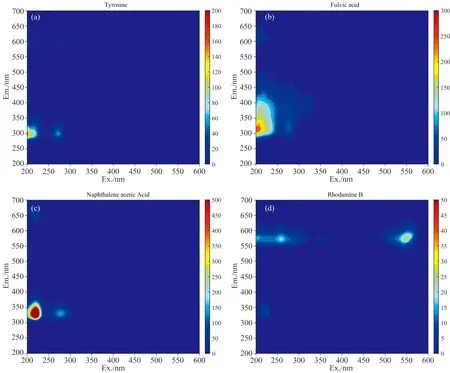
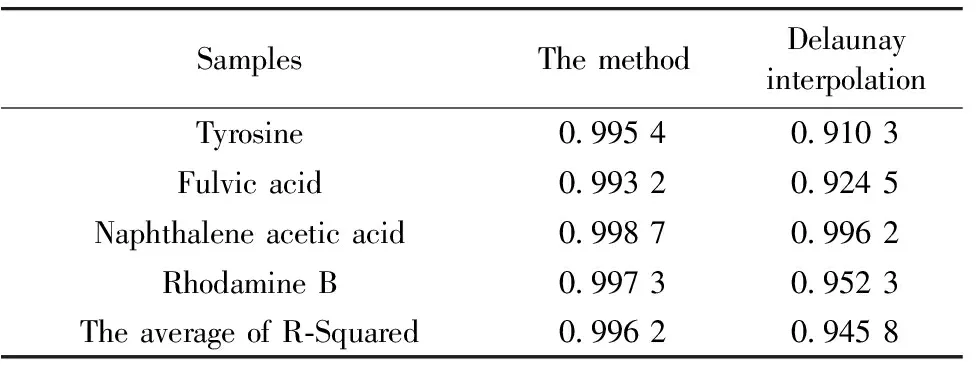
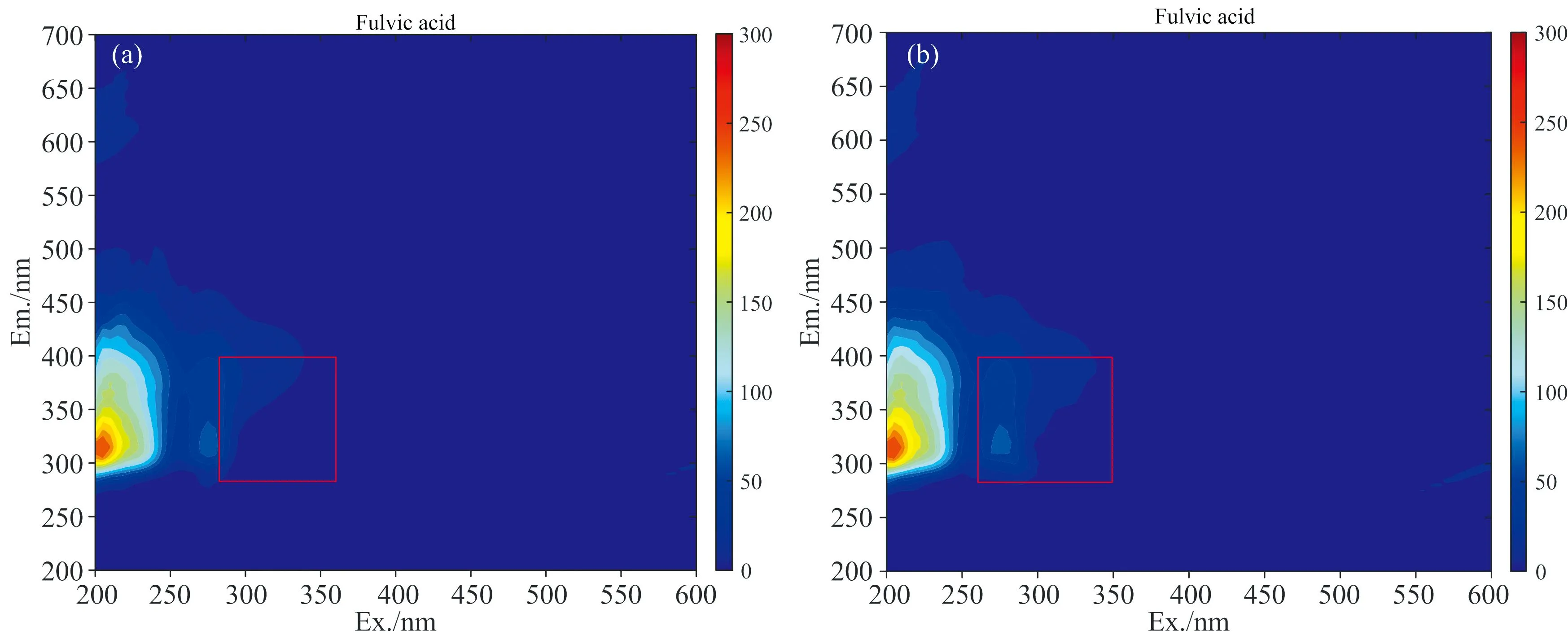
由于拉曼散射是通过空白扣除法进行校正的, 所以原始光谱的瑞利散射数据也将扣除部分。 因此会存在瑞利散射信号比物质荧光强度弱的情况。 我们将从散射峰与物质峰的荧光强度大小关系进行考虑, 将其分为h≤1/2H和h>1/2H两大类。 首先介绍h≤1/2H的情况。 我们对其四个端点: A、 B、 C、 D分别进行评估。 对于A端点, 当h1≤1/2H0, 且y(A)≈0时表示散射峰与物质峰不存在重叠区域, 采用置零法对R1区域进行有效数据替换处理; 当0 图2 酪氨酸在(a) 210 nm, (b) 260 nm, (c) 270 nm, (d) 275 nm激发波长下的荧光发射光谱 而当h>1/2H时, 将存在三种情况, 即无重叠、 微弱重叠和严重重叠。 以B点为例进行探讨, A、 C和D点的情况根据上文依次类推。 当h1>1/2H1,y(B)≈0时, 如图2(b)所示, 表明散射峰与物质峰无重叠, 可用置零法将R1区域内数据替换为0。 当0 将这五种情况列表如表2所示。 需要注意的是对于瑞利散射而言其一般具有两个边界端点, 如果两个端点所判断的情况不一样, 则需要根据优先级关系进行进一步判断处理。 优先级关系为: 类别5>类别4=类别2>类别3=类别1。 表2 自适应算法所对应的五类情况 如图3(a), (c), (e), (g)分别是酪氨酸、 黄腐酸、 萘乙酸和罗丹明B的原始光谱图, 酪氨酸、 萘乙酸和罗丹明B的浓度均为40 μg·L-1, 黄腐酸的浓度为5 mg·L-1, 以此为例, 其他情况均可类推。 不难看出, 酪氨酸和黄腐酸与拉曼光谱重叠较为严重, 存在严重重叠区域。 通过空白扣除法, 扣除了原始三维荧光光谱的背景干扰和拉曼散射后, 所得光谱图如图3(b), (d), (f), (h)所示。 通过对比图3(a), (b)和图3(c), (d)可以看出, 即使物质荧光区域与拉曼散射区域严重重叠, 该方法也能起到很好的校正效果。 由此论证通过空白扣除法校正拉曼散射是合理有效的。 图3 (a) 酪氨酸、 (c) 黄腐酸、 (e) 萘乙酸、 (g) 罗丹明B的原始三维荧光光谱图; 其拉曼散射校正后的光谱图分别为(b)、 (d)、 (f)、 (h); 校正后的三维荧光光谱图上方两条色条分别表示一阶瑞利散射和二阶瑞利散射区域与物质峰的重叠程度, 蓝黑色、 橙色和红色色条分别对应无重叠、 微弱重叠和严重重叠 通过图3(b), (d), (f), (h)也可以看出, 对于低浓度样品而言, 仅仅通过空白扣除法是无法完全去除瑞利散射干扰的, 这与理论相符。 因此对于低浓度并且物质荧光信号存在与散射区域重叠较为严重的样品来说, 亟需一种有效的去除瑞利散射的方法。 按照1.4节的方法, 综合考虑物质峰与散射区域峰值的荧光强度和重叠程度, 对光谱进行重叠等级评估, 结果如图3(b), (d), (f), (h)三维荧光光谱上方的色条所示。 上方第一条色条表示一阶瑞利散射与物质峰的重叠程度, 上方第二条表示二阶瑞利散射与物质峰的重叠程度。 蓝黑色代表无重叠, 橙色代表微弱重叠, 红色代表严重重叠。 不难得出, 罗丹明B的重叠情况和程度相对于其他三种物质来说更为复杂, 这与事实相符。 根据2.1节中瑞利散射区域与物质峰重叠程度的评估结果, 分别对酪氨酸、 黄腐酸、 萘乙酸和罗丹明B这四种典型的有机化合物进行了相应的算法处理。 校正后的三维荧光光谱图如图4(a), (b), (c), (d)所示。 与原始三维荧光光谱图对比, 可以发现物质荧光光谱区域结构完整, 大量信息得以有效留存, 瑞利散射和拉曼散射完全去除。 即使光谱重叠严重的罗丹明B的三维荧光光谱经过处理后形状也未失真, 证明了本文方法去除散射干扰的有效性。 图4 (a) 酪氨酸、 (b)黄腐酸、 (c)萘乙酸、 (d)罗丹明B基于自适应方法校正后的三维荧光光谱图 因为黄腐酸是天然有机化合物, 广泛存在于自然界中, 并且物质荧光区域和散射区域存在严重重叠情况。 所以以黄腐酸为典型物质, 将本文方法与现阶段研究中采用最多的Delaunay三角形内插值法进行对比。 我们分别采用[16, 18]、 [10, 10]、 [22, 22]、 [18, 16]为最佳参数的一阶瑞利散射、 一阶拉曼散射、 二阶瑞利散射和二阶拉曼散射数值设定进行了Delaunay插值, 结果如图5(b)所示。 可以看出红色方框区域内的荧光信号相对于本文所使用的方法而言出现严重失真, 存在过拟合现象。 说明Delaunay插值方法对存在严重重叠干扰的适应性较弱。 并对四种有机化合物的共20个样本, 分别用这两种方法进行了散射校正处理, 以重叠区域散射校正后的数据进行浓度回归, 所得决定系数R-squared的值列表如表3所示, 本文方法的平均决定系数为0.996 2, 相对于Delaunay插值法所得的平均决定系数提高了5.04%, 进一步证明了本文方法保持物质荧光光谱区域的结构特征和去除散射干扰的合理有效性。 表3 四种有机化合物经本文方法和Delaunay插值法散射校正后进行浓度回归预测所得的决定系数值 图5 黄腐酸散射校正后的三维荧光光谱图 为验证本文方法在实际应用场景中的可靠性和通用性, 我们通过模拟突发污染实验对所得水样进行了水质监测。 因为罗丹明B是一种常见的致癌染料, 经常在印染厂附近的河流中发现。 所以我们拟采用自来水和罗丹明B进行实验, 共获得30个样品。 利用PARAFAC模型计算30个样品的四个PARAFAC分量的载荷, 如图6所示, 可以看到组分四在第9和第10个样品之间有明显的变化。 这与加入罗丹明B的时间相符, 进一步验证了本文方法修正三维荧光光谱中瑞利散射和拉曼散射的合理性, 同时论证了此方法具有普适性, 可以用于实际应用场景之中。 图6 模拟突发污染水样的四种PARAFAC组分载荷随时间的变化趋势 基于散射峰与物质峰的荧光强度和光谱重叠程度, 提出了一种自适应的三维荧光光谱去散射方法。 其过程包括: 获取样品的三维荧光光谱数据→通过空白扣除法扣除拉曼散射和背景干扰→根据散射峰与物质峰的荧光强度和光谱重叠程度将样品光谱分为五种情况对应三种算法分别进行数据处理→得到散射校正后的三维荧光光谱数据。 在四种典型有机化学品的去散射实验中, 与原始光谱、 空白扣除法和Delaunay插值法对比, 利用本文方法去散射后的三维荧光光谱数据相比单一的使用空白扣除法更好地校正了瑞利散射的干扰。 并且以重叠区域散射校正后的数据进行浓度回归, 本文方法所得的平均决定系数为0.996 2, 相比于Delaunay插值法提高了5.04%, 进一步证明了本文方法有效地避免了过拟合现象的发生, 保持了物质荧光光谱区域的结构特征。 此外, 还进行了模拟突发污染实验, 对水样进行监测。 结果表明, 此方法在提高三维荧光光谱数据处理的适应性和准确性方面具有潜力, 可用于实际场景之中。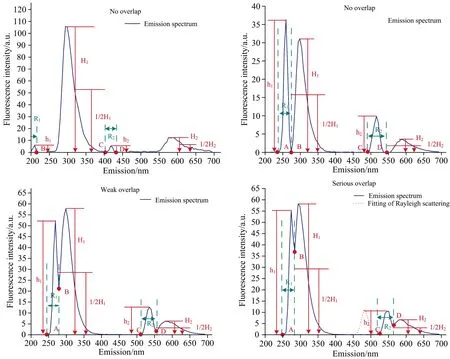
2 结果与讨论
2.1 拉曼散射与背景干扰校正
2.2 三维荧光光谱校正
2.3 模拟突发污染水样的PARAFAC分析

3 结 论
