混合颗粒系蒙特卡罗消光模型及反演方法

黄 茜, 苏格毅, 孙存金, 邓 飞, 陈 军, 杨荟楠, 苏明旭

上海理工大学能源与动力工程学院, 上海 200093

引 言

消光光谱法[1]原理简单、 测试快捷、 结果准确, 广泛应用于悬浮粉尘[2]、 火焰烟尘[3]、 湿蒸汽[4]、 乳剂[5]中颗粒粒径和浓度分析。 近年来, 很多学者对消光法颗粒测量进行深入研究, Zhang等[6]研究颗粒物的折射率与波长关系及对消光法的影响, 指出折射率的变化可导致消光法粒径测量偏差, 处理消光谱数据时, 应考虑颗粒的色散特性; Tuersun等[7]关注到金纳米球溶液中消光光谱对粒径的敏感性, 研究了共振粒子的消光光谱法测量多分散金纳米球的粒径分布和浓度问题; Krogsøe等[8]根据消光光学微粒计数器输出信号, 测得油液中颗粒污染物的真实粒度。 以上研究成功应用至单一类型颗粒系的测量, 不过在现实中诸多被测对象包含了两种甚至多种颗粒物, 称为混合颗粒体系, 此时既有的Mie散射理论和Lambert-Beer定律构建的消光模型将不再适用。

蒙特卡罗方法(Monte Carlo method, MCM)是一种概率统计方法, 已成功应用于颗粒系中光复散射(多次散射)和颗粒两相及多相流研究。 Dap等[9]发展了基于蒙特卡罗原理的消光光谱法颗粒粒径和浓度的反演程序, 并通过可见光和红外光谱实验数据进行验证; Lebovka等[10]建立了蒙特卡罗数值模型, 模拟光束在圆柱体颗粒悬浮液中的传递过程, 研究颗粒等效截面及与Lambert-Beer定律的偏差, 探究碳纳米管的光学性质; 肖新宇等[11]运用蒙特卡罗方法研究了消光法颗粒粒径测量中发散光束的影响, 并实现了粒径反演修正。 鉴于蒙特卡罗法模拟具有过程清晰可追踪、 接近实际的优势, 作者建立基于蒙特卡罗原理的消光模型, 预测混合颗粒体系消光谱, 并研究颗粒类型、 混合比对消光特性的影响。 同时借助全局优化算法, 实现混合颗粒系的颗粒粒径和混合比同步反演。

1 原 理

1.1 消光光谱法原理

光谱消光法基于Lambert-Beer(LB)定律, 当一束光强为I0的平行单色光, 穿过离散颗粒物两相体系会发生散射和吸收并导致透射光的衰减, 将入射光强I0与透射光强I之比的对数形式称为消光值, 可以描述颗粒物对某一波长光吸收/散射的强弱与颗粒物浓度及光程的关系, 即

ln(I0/I)=πcnLR2kext=cnLCext

(1)

式(1)中,cn为颗粒数目浓度,R为被测颗粒半径,L为光程,kext为消光系数,Cext为消光截面。

LB定律适用于单一颗粒系的单分散情况, 在不同波长条件下运用式(1), 可获得消光谱信息并确定颗粒系粒径分布。 不过, 对于混合颗粒体系, 该定律适用性遇到困难, 不同类型颗粒光散射特性不同, 其消光系数/截面也不一致, 在模型中很难表达并使得理论消光值无法计算。 此时, 引入蒙特卡罗方法, 构建新的消光谱预测模型。

1.2 蒙特卡罗方法

根据消光法原理, 蒙特卡罗方法核心思想是将物理上的入射光束按照“光子”概念抽象并做离散化处理, 通过光子与体系中颗粒的相互作用将光子历程分为透射、 散射与吸收, 分类统计各去向的光子数, 进而得到其消光值。 根据其特点, 易于引入到颗粒及混合颗粒多相体系的模拟计算。

如图1所示, 两相体系中混合了两种球形颗粒: 黑色颗粒Ⅰ、 蓝色颗粒Ⅱ。 几何参数L为样品池厚度(光程),dT、dR分别为发射器与接收器的直径, 2H为样品池上下边界距离,S为发射器或者接收器与样品池的距离,l为随机散射自由程。 通过统计获取接收器光子数, 即可模拟在一定颗粒粒径、 浓度和光波长条件下混合颗粒系中光波行为并计算消光值。

图1 光子在混合颗粒体系中传播过程示意图

图2给出了蒙特卡罗模型计算流程, 根据输入初始参数颗粒半径R、 波长λ、 体积浓度cv, 进行消光值计算。 假设光束沿着图1中x轴方向传播, 平行光入射。 以发射器中心点为原点, 光子的初始出射坐标(x0,y0)

(2)

图2 蒙特卡罗模型算法流程

式(2)中,ε1为[0, 1]区间内服从均匀分布的随机数。

光子刚进入样品池时坐标为(S,y0), 若光子和颗粒发生碰撞, 则光子首次发生散射的坐标(x1,y1)可以表示为

(3)

(4)

式中,εl是[0, 1]范围内均匀分布随机数,τ为浊度, 其在混合颗粒系中, 仍可定义为[12]

τ=cn×Cext

(5)

其中, 对于混合颗粒体系, 需要判断颗粒类型

(6)

式(6)中,ε2是在[0, 1]区间内服从均匀分布的随机数, 混合比φ指颗粒Ⅱ在整个混合颗粒体系中所占的数目比, 例如:φ=0时全为颗粒Ⅰ,φ=1时则全为颗粒Ⅱ。 当前颗粒的消光截面Cext可由Mie散射理论计算[1]。 颗粒系数目浓度cn为

(7)

通常进入两相体系的光子可能被颗粒吸收、 被接收器直接接收(透射)、 未被接收器接收(逃逸)或在样品池里再次散射, 定义散射截面和消光截面比值为反照率a

a=Csca/Cext

(8)

其中: 消光截面Cext和散射截面Csca由Mie散射理论计算得出。 根据设定条件判断光子的下一事件

(9)

式(9)中,ε3是[0, 1]区间服从均匀分布的随机数,n为散射次数。

对于多次散射, 光子与颗粒碰撞后的空间散射角分布可以由Henyey-Greenstein相函数[13]确定, 散射角θ0的抽样表示为

(10)

式(10)中,εθ0是另一个[0, 1]范围内随机数,g是不对称因子。 发生第一次散射时, 光子散射方向θ1=θ0。 重复式(4)—式(10), 根据散射自由程与散射角, 第n次散射时的光子散射方向为θn=θn-1+θ0(n>1), 光子散射后的坐标为

(11)

根据式(9)条件判断并统计其最终去向, 进行下一个光子历程, 直到完成所有光子计算, 统计各个物理过程的光子数, 得到散射介质的消光特性。 消光谱可表示为

ln(I0/I)=ln(Nset/N)

(12)

式(12)中,N为接收透射光子总数,Nset为设定光子数。

2 数值结果

2.1 计算参数

按照前述模型编制计算程序, 模型尺寸(参见图1)、 颗粒性质、 可变参数均列于表1中, 介质为水(折射率m=1.33), 颗粒Ⅰ选取聚苯乙烯(折射率m1), 颗粒Ⅱ选取高密度玻璃(折射率m2), 忽略颗粒的吸收特性。 根据前期初步数值结果分析, 设定光子数为105进行计算。

2.2 光子去向统计

使用蒙特卡罗模型计算程序模拟R=0.2 μm的颗粒Ⅰ的光子去向, 将经过一次与多次散射后被接收器接收到的光子分为单散射与复散射, 定义从前向边界出射的其他逃逸光子为前向逃逸, 反之为后向。

图3可以看出, 在给定粒径下, 随着波长增大透射光子数逐渐增多。 按光散射理论, 波长增大, 亚微米区颗粒的无因次参数α(α=2πR/λ)减小, 消光系数减小, 再结合式(4)计算出射光子随机自由程, 光子准直透射的概率增大。 在当前光学厚度下, 散射光较微弱, 且以单散射为主, 其随光波长增大而减小。 由于接收器位置设定离样品池较远, 接收器尺寸小, 最终进入接收器散射光有限(计算消光时限定只考虑透射光子), 逃逸发生的光子以前向为主, 数目随光波长增大逐渐减小。

图3 光子事件统计

2.3 蒙特卡罗方法验证

为了验证蒙特卡罗方法预测消光谱的准确性, 首先分别考虑颗粒Ⅰ和颗粒Ⅱ的单一颗粒系情况, 采用蒙特卡罗方法仿真计算, 研究颗粒系的消光谱变化, 并和Lambert-Beer模型进行对比。

图4给出两种颗粒各自的消光谱, 颗粒半径分别为0.2、 0.8、 2.0 μm。 可以看出, 随着颗粒粒径的增大, 消光谱有明显变化, 表明其对于粒径是非常敏感, 有利于粒径的反演; 当粒径超出亚微米区后(如2.0 μm), 消光系数随着无因次参数α的增大而呈现振荡现象; 而相同粒径下, 由于颗粒Ⅰ和颗粒Ⅱ自身折射率不同, 导致消光谱趋势不同。 通过结果对比看出蒙特卡罗方法预测与Lambert-Beer模型在数值上吻合, 相对误差均在±2%以内, 表明蒙特卡罗方法适用于颗粒系的消光谱预测。

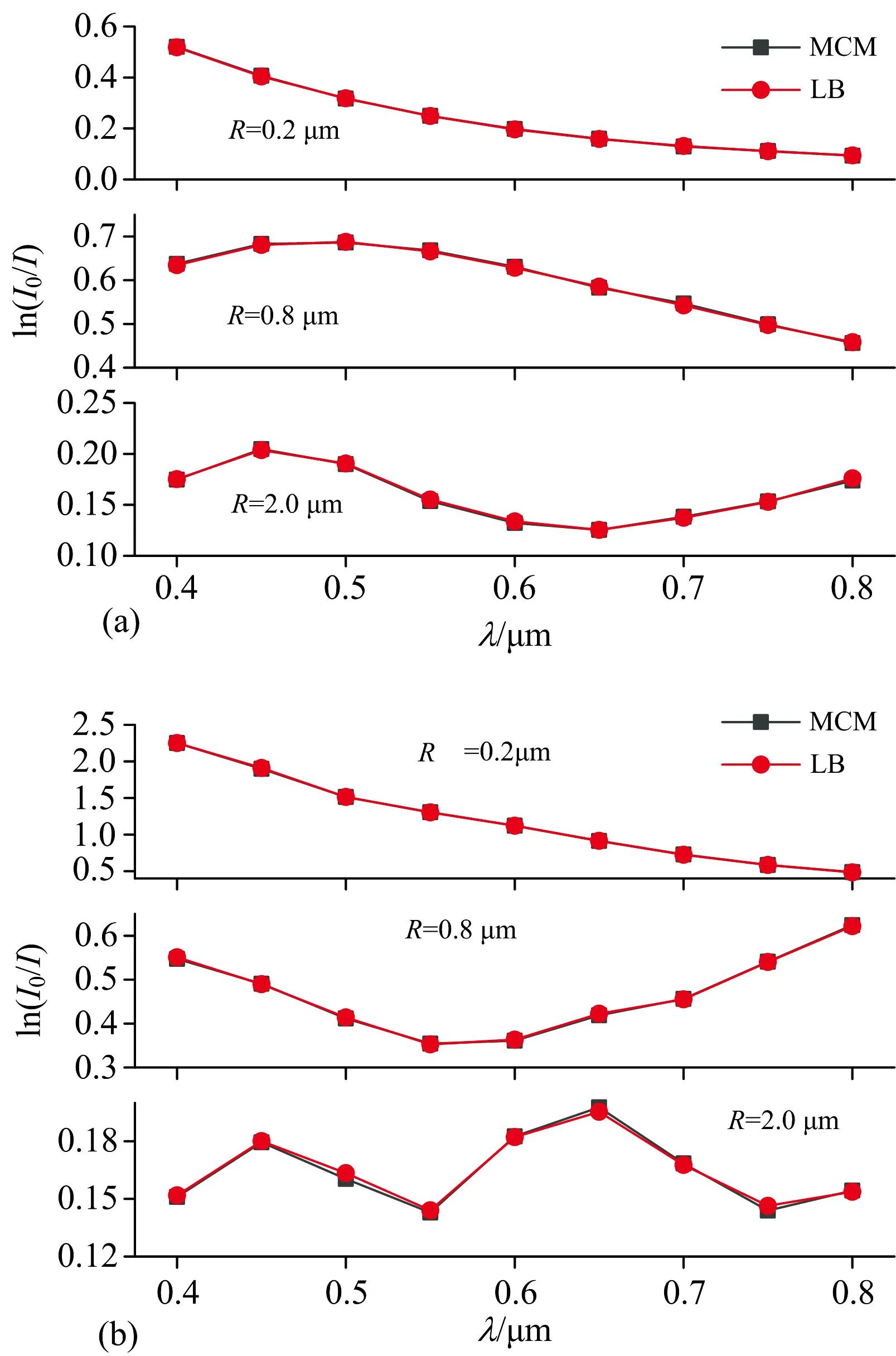
图4 蒙特卡罗方法与Lambert-Beer模型的消光谱对比

单一颗粒系体积浓度cv与消光值存在线性关系[见式(1)], 其并不影响消光随光波长的变化趋势即归一化的消光谱, 对于混合颗粒系, 同样通过数值模拟进行了验证。 后续计算中, 仅以cv=2×10-5进行计算, 不考虑cv对消光谱的影响。

2.4 混合颗粒系消光特性

将模型拓展到由颗粒Ⅰ与颗粒Ⅱ组成的混合颗粒系中,R1=0.2 μm不变,R2不同时, 改变两种颗粒的数目混合比φ, 进行消光谱预测。

图5(a)、 (b)、 (c)给出了不同混合比条件下颗粒系的消光谱。 随着入射光波长的增大, 消光谱呈递减趋势, 颗粒Ⅱ的粒径对消光谱曲线有明显影响。 当R2为0.15 μm, 图5(a)中消光谱随波长的增大逐渐趋缓, 而当R2增至0.3 μm, 由于消光系数差异, 图5(c)中消光谱随波长增大趋势更近于线性。 对于给定波长和粒径, 从图5(d)可以看出: 颗粒系的消光值随混合比增大而递增, 而波长减小时, 消光值由线性趋势向非线性趋势转变, 且两种颗粒消光特性差别越大, 非线性趋势越明显, 因为两种颗粒类型不同, 当入射光波长改变时, 颗粒的消光特性相应变化。 上述结果说明, 在一定浓度下混合颗粒系的消光由颗粒类型、 混合比、 颗粒粒径和光波长等共同决定, 如混合比对消光谱的影响与不同类型颗粒的散射特性差异有关, 其受制于粒径和波长取值, 二者同时影响颗粒的消光和散射效应, 据此可根据消光谱同步反演出颗粒粒径与混合比。

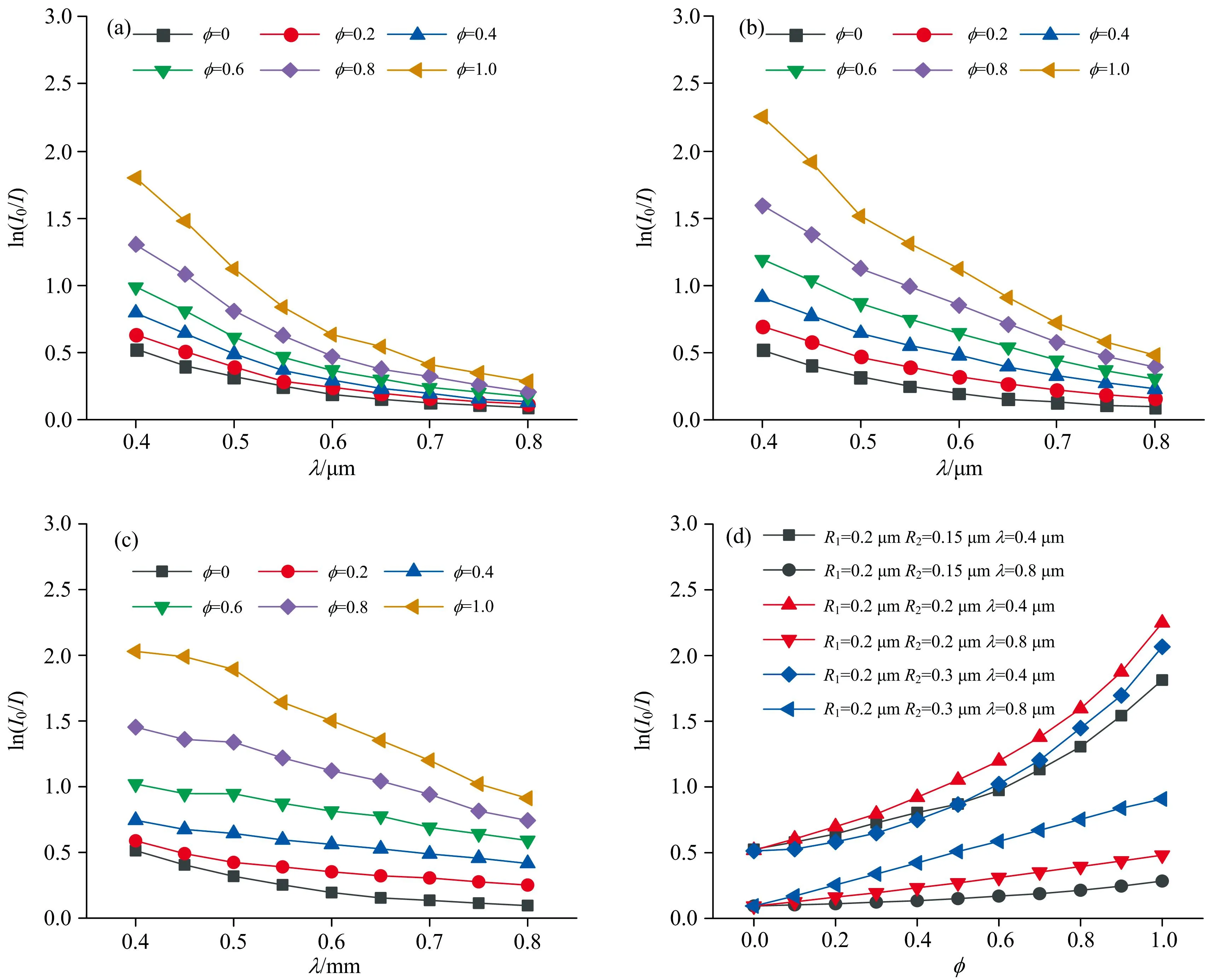
图5 混合颗粒系消光预测

3 反 演

3.1 反演方法

最优化算法是消光谱反演求解颗粒粒径时最为常见方法[14], 混合颗粒系可借助蒙特卡罗模型获得理论消光谱, 不过, 由于两种甚至多种颗粒类型的存在, 增加了混合比等待定参数, 反演难度会增加。 采用消光谱误差构建目标函数

(13)

式(13)中: ln(I/I0)sim是理论消光谱, ln(I/I0)set为设定值的消光谱,j为计算消光谱的波长数,j=1, 2, …,M。 在设定反演参数的上下限范围内寻优搜索最佳粒径与混合比, 使目标函数达到最小, 从而实现参数的反演。

为更好地验证反演效果, 采用三种全局最优算法对所构造的目标函数进行寻优, 分别是优化遗传算法(improved genetic algorithm, IGA)[15]、 粒子群算法(particle swarm optimization, PSO)[16]、 改进差分进化算法(improved differential evolution, IDE)[17]。 其中, IGA具有较好全局收敛性, 经优化设定最大迭代次数为500、 种群尺度为50、 交叉概率为0.8、 变异概率为0.045, 以提高算法稳定性。 PSO采用自适应惯性权重, 对适应度值小于平均值的粒子进行小波变异, 增强群体多样性, 并使粒子在解空间的其他区域进行搜索, 防止粒子群算法陷入局部最优, 设定种群尺度为500, 迭代次数在50～60之间。 IDE引入了自适应控制参数因子对缩放因子和交叉因子进行优化, 选定交叉因子为0.85, 缩放因子上限和下限分别为0.5和0.3, 种群尺度为50, 并设定最大迭代次数为50, 以提高优化效率。

如图6所示, 进行颗粒和混合比的单参数、 双参数和三参数同步反演。 分别为: ①已知混合颗粒系粒径, 对混合比进行反演; ②已知颗粒系混合比, 对两种颗粒粒径进行反演; ③两种颗粒类型粒径相同或不同时, 对粒径与混合比进行同步反演。 分别选取R1=R2=0.2 μm、φ=0.8和R1=0.2 μm、R2=0.3 μm、φ=0.4两种情形, 设置粒径参数上下限为R∈[0.05 μm, 1 μm]、 混合比φ∈[0, 1], 计算波长数M=9。

图6 反演算例

3.2 反演结果分析

图7(a)为已知颗粒粒径R1和R2, 求解其混合比, 可以看出: 无论颗粒粒径是否相同, 三种优化算法反演混合比与设定值相对误差均小于1.5%。 图7(b)给定颗粒系的混合比φ=0.4, 反演两种颗粒的粒径, 为双参数反演, 粒径相对误差在3%以内, 均较为精确。 为验证算法稳定性, 以IGA为例, 进行三次重复反演, 其粒径R1、R2的标准差为8.2×10-4与1.1×10-3。 图7(c)、 (d)为三参数同步反演,R1=R2时,φ的反演误差仍小于2%, 但R1反演误差可至约8%(PSO算法); 当R1≠R2时, 三参数的反演误差增大,R1、R2的误差接近9%。

图7 混合颗粒系参数反演结果

此外, 三种算法的反演时间不尽相同, 双参数反演时, IGA和IDE的一次计算时间约需40 min, 而PSO反演耗时为其数倍。 总体上, IGA算法效果较好且更加稳定, 就本文算例来看, 所有算例下反演误差均在10%以内。

4 结 论

研究了两相颗粒系光散射效应, 建立了蒙特卡罗原理的混合颗粒体系消光预测模型, 获得聚苯乙烯和高密度玻璃微珠混合颗粒系的消光谱, 据此讨论了混合比、 混合颗粒粒径对消光谱的影响。 根据预测消光谱对颗粒粒径与混合比同步反演。 结果表明:

(1)在单一颗粒系中, 蒙特卡罗方法与传统Lambert-Beer模型的计算结果较一致, 相对误差均在±2%以内。

(2)对混合颗粒系的消光谱预测, 不同混合比的消光谱均分布在φ=0与φ=1之间, 随颗粒Ⅱ粒径不同, 消光谱趋势相应变化, 颗粒Ⅱ的占比对消光谱有明显影响, 消光值随着混合比递增, 当波长减小时增长趋势由线性向非线性转变, 即不同颗粒类型影响了消光谱的数值大小与趋势。

(3)对混合颗粒系的消光谱反演, IGA、 PSO、 IDE算法均可实现单参数和多参数同步反演。 其中, 仅对混合比参数反演时误差最小, 相对误差在1.5%以内, 随反演参数增加, 误差增大, 三参数反演时, 混合颗粒的粒径变化对反演有影响, 但算例中误差均在10%以内。