基于差分进化变分模态分解的直升机行星轮系故障监测

孙灿飞，彭德润

（1.上海工程技术大学航空运输学院，上海 201620；2.航空工业上海航空测控技术研究所测控技术产品部，上海 201601）

近年来，航空装备故障诊断技术发展迅猛，在飞机和发动机的健康管理系统中得到广泛应用。相比其他故障，早期故障引起的振动信号幅度较小，容易淹没在正常的振动信号背景中，尤其对于行星轮系复杂的信号形态，微弱的故障信号更加难以捕捉。因此，早期故障更容易被忽略，而一旦故障持续发展将导致后期严重的飞行安全事故。2016 年，挪威一架H225“超级美洲豹”直升机坠毁，就是因为结构疲劳造成的行星轮系早期裂纹没有及时得到预警，最终造成灾难性的事故。因此，开展直升机行星轮系故障监测方法的研究具有重要的意义［1］。

直升机主减速器内部复杂的齿轮传动形式和行星轮系自身独特的齿轮结构造成传感器测量到的振动信号呈现出非常复杂的信号形态［2］。首先，行星轮系所在的主减速器内各齿轮部件内部结构紧凑，各齿轮部件旋转频率和谐频及故障特征频率等多频率成分组合在啮合频率和谐频附近，形成复杂边带信号，且多阶谐波出现频谱交织，使信号更加复杂。其次，行星轮系本身的振动信号成分复杂，包括出现在行星齿轮运行过程中的特征频率成分、出现在啮合频率和谐频附近的成组边带成分、经多界面耦合传播而来的支承轴承和其他定轴齿轮等旋转部件的特征频率成分等。再次，行星轮系故障，尤其是早期故障引起的微弱振动信号经传感器复杂传输路径衰减后，信号被进一步削弱，且大传动比决定了齿轮故障信号的特征频率极低，加之低速重载的复杂运行条件使得低频振动成分的噪声污染非常严重。因此，如何从具有复杂信号背景的直升机行星轮系振动信号中削弱甚至消除非故障敏感信号分量的干扰，增强故障敏感信号分量并进行有效提取是直升机行星轮系故障监测研究的热点和难点。

根据行星齿轮箱振动信号理论模型与频谱特性，齿轮故障会引起啮合频率及其谐频附近的边带频谱变化［3］，提取边带信号中含有故障齿轮特征频率的信息进行故障识别，可解决复杂信号背景造成的故障频率特征提取难题，提高诊断准确率［4］。因此采用模态分解与联合解调的方法得到了广泛关注。

Zhao等［5］应用经验模态分解（Empirical Mode Decomposition，EMD）方法分解行星齿轮箱的振动信号，并从中遴选敏感分量提取故障特征进行故障诊断。由于EMD方法易产生模态混叠、过包络、欠包络等问题，Smith等［6］提出了局部均值分解方法，但其抗干扰能力差，算法不易收敛。Frei 等［7］提出了本征时间尺度分解方法，消除了边缘效应和负频率等的影响，瞬时频率的计算精度较高，适用于非平稳非线性信号，但仍然存在信号失真等问题。李志农等［8］应用经验小波分解方法有效识别了转子碰摩故障，该方法解决了模态混叠等难题，但需要指定频带数量，对于复杂振动信号来说容易损失含有故障信息的边频带信息。2014 年，Dragomiretskiy 等［9］提出了变分模态分解（Variational Mode Decomposition，VMD）算法，其广泛应用于机械故障诊断领域［10-11］，该方法是一种非递归的分解算法，不存在端点效应，可有效分离频率接近的谐波信号，且具有较好的噪声鲁棒性。

针对直升机行星轮系故障监测中复杂信号背景带来的难题，本文提出了基于差分进化变分模态分解（Differential Evolution Variational Mode Decomposition，DEVMD）的直升机行星轮系故障监测方法。本方法集成了重叠组收缩（Overlapping Group Shrinkage，OGS）算法作为前置滤波对背景噪声进行抑制，结合DEVMD方法高性能的模态分解能力剥离出振动信号中其他旋转部件的信号分量，获得行星轮系的故障敏感信号分量并提取故障指示因子，实现了直升机行星传动轮系的故障监测。

1 故障监测理论与方法

1.1 基于OGS的前置降噪

由于传感器测量的故障信号微弱，低速重载的运行条件和恶劣的工作环境导致信号容易受到背景噪声的干扰，尽管相比于其他信号分解方法，VMD 算法的噪声鲁棒性较好，但噪声增大到一定程度后，用该方法进行信号分解仍然会出现模态混叠、中心频率偏移等现象，导致模态分解错误，因此在进行后续的信号处理之前，须进行前置降噪。

近年来，基于稀疏性的信号去噪、去卷积、恢复、重构等算法得到了广泛的应用。2014 年，Chen 等［12］提出了OGS算法，该算法适应于具有成组稀疏特性（即大幅值数据以组的形式存在）的信号，非常适用于对故障引起的周期性冲击信号的降噪。OGS 算法基于重叠组的收缩，将具有相同组特性的稀疏信号进行等比例处理，因此具备平移不变性，避免了块效应，在最大化有用信息的同时抑制了噪声信号。OGS 算法的优点包括：①转化信号降噪问题为最优化问题进行求解，得到的稀疏解中大幅值信号成分得到有效保留，在抑制噪声的同时有效保留了信号中的有用成分；②计算复杂度低且不需要调节算法参数。因此本文引入OGS算法作为前置降噪方法，抑制背景噪声，降低噪声方差，提高了VMD算法的分解性能。

假定信号表达式为

式中：y（i）为振动传感器测量的含噪信号；x（i）为具有成组稀疏性的有用信号；w（i）为环境背景噪声；I ＝｛0，1，…，N-1｝，N为数据点数量。

为从y（i）中最大程度估计出x（i），OGS算法将式（1）表达的信号降噪问题转化为最优化问题：

罚函数R［x（i）］的定义为

式中：J ＝｛0，1，…，M-1｝，M为组数。

因此，最终的代价函数为

OGS算法流程如下。

①确定输入信号和参数：y、λ、M。

②确定输出信号：x。

③初始化：x（i）＝y（i），x（i）≠0。

⑥重复步骤④和步骤⑤，直到满足收敛条件。

⑦得到降噪后的信号x。

1.2 基于DEVMD方法的故障敏感信号分量提取

在直升机行星轮系的振动信号频谱中，除了有与行星轮系故障相关的信号分量外，还包括一级减速主从动齿轮、二级减速主从动齿轮、尾传动齿轮和各附件齿轮等部件的啮合振动信号分量。为了消除其他无关信号分量的影响，有效提取行星轮系的故障敏感信号分量，本文提出了基于DEVMD 方法的故障敏感信号分量提取方法。该方法结合VMD 算法与差分进化（Differential Evolution，DE）算法对振动信号进行自适应分解，从分解后的模态分量中遴选出最优故障敏感信号分量进行包络谱分析与故障识别。

相比于其他模态分解方法，VMD算法避免了模态混叠与端点效应，具有可分解频率相近成分等优点，其分解的精度主要受到以下两个参数影响。

①模态数量K。K确定了要分解的模态分量的数量，并可根据K 采用均匀分布、随机取值和赋值零等方式初始化中心频率。K 取值过小，模态分量之间会产生混叠；K 取值过大，模态分量的完整性会受到影响，同时会增加计算复杂度。

②惩罚因子α。α 实现了对带宽的约束：α 取值过小，分解得到的模态分量的带宽过大，对噪声的鲁棒性就较差，且各模态分量间可能出现交叉；α 取值过大，分解得到的模态分量的带宽过小，就容易出现中心频率偏移的情况，导致分解失败。

针对K与α的选择，文献［13］以包络谱熵为目标函数，采用粒子群算法对VMD 算法的最佳参数组合进行搜索，实验结果表明该方法的分析效果准确有效。文献［14］为了自适应确定变分模态分解的模态数量，以互信息为判据对原方法进行了迭代停止条件的改进，结合Teager 能量算子对单分量信号解调速度快、精度高的优点，提出了Teager-VMD时频分析方法。上述方法针对VMD 算法的参数选取，主要采用智能算法进行多次迭代优化选取，存在计算时间长、效率低等缺陷。另外，VMD算法的中心频率采用随机和均匀分配两种方法，当中心频率误差较大时，无法正确实现信号分解。

针对上述情况，本文提出了自适应参数的DEVMD方法，利用功率谱密度先验知识初始化中心频率，并基于正交能量差采用DE 算法搜寻最佳的K与α的组合，详细处理流程如图1 所示。该方法既保证了模态分解的准确性，又保证了分解的模态分量具有一定的物理意义。

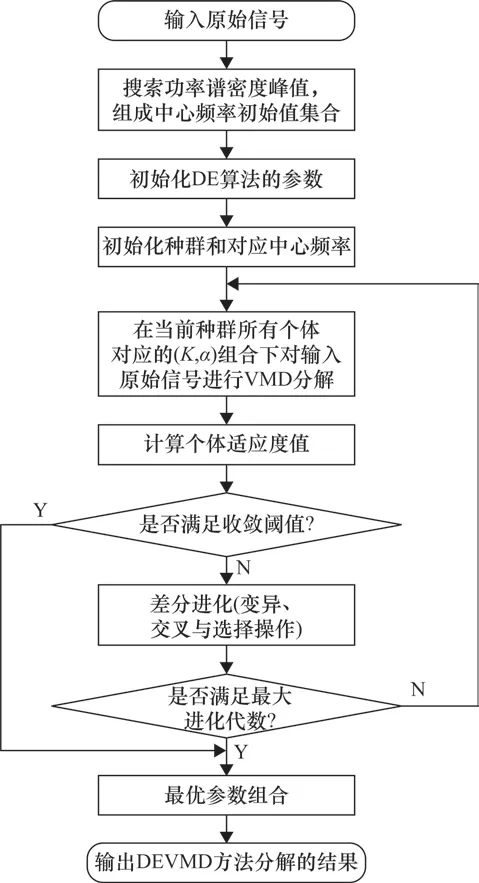
图1 DEVMD方法处理流程

DEVMD方法的详细处理流程如下。

①输入原始信号x（t）。

②计算信号的功率谱密度，按照功率谱密度峰值由大到小搜索前Kmax个峰值，并记录其相对应的频率，组成中心频率初始值集合｛ωinitial｝。

③初始化DE算法的参数，包括种群规模N、缩放比例因子F和交叉概率CR。

④初始化种群pi＝（pi，1，pi，2，…，pi，D），i ＝1，2，…，N，D为维数；初始化种群个体对应的中心频率，从｛ωinitial｝中抽取前K个频率作为初始化中心频率。

⑤在当前种群所有个体对应的（K，α）组合下，对输入原始信号进行VMD分解。

⑥计算个体适应度值。由于输入振动信号所分解的各模态分量具有各自的物理意义，彼此独立，具备正交性，根据帕塞瓦尔定理，分解的正交模态分量的能量之和与原始信号的能量相等，因此本文选取正交能量差作为DE算法优化的适应度函数：

⑦若个体适应度值满足收敛阈值的要求，即Ediff≤（0.01 ～0.02）Ex，则停止寻优，否则进行种群进化。

⑧对当前种群进行差分进化，产生新一代种群。

a.变异操作。

式中：g为进化的代数；r1，r2，r3∈（1，2，…，N），与i 均互不相同。

b.交叉操作。

式中：j∈（1，2，…，D）；r为［0，1］的随机整数。

c.选择操作。

基于贪婪机制在父代个体与交叉后向量中选择子代个体，通过式（8）确定。

式中：f为个体的适应度函数。

⑨若当前进化代数满足中止条件，则停止寻优，否则继续进行寻优。

⑩停止寻优，得到最优适应度值个体所对应的（K，α）组合。

1.3 基于峭度-包络谱熵的故障监测

从分解的BIMF分量中选取中心频率在行星传动轮系啮合频率附近的分量作为故障敏感信号分量，选取峭度-包络谱熵（Kurtosis-Envelope Spectrum Entropy，KE）作为故障指示因子实现故障监测。

峭度是反映随机变量分布特性的数值统计量，是归一化4 阶中心矩。峭度是无量纲参数，定义为

包络谱熵计算公式为

式中：（ρ1，ρ2，…，ρn）为包络谱信号的幅值概率密度。

由于峭度对冲击信号特别敏感，通常作为早期故障信号的筛选指标。另外，包络谱熵用于衡量严重故障情况下信号的周期性特征。综合峭度、包络谱熵分别对早期故障、严重故障更加敏感的特点，本文提出了峭度-包络谱熵，定义为

周期性冲击信号是齿轮局部故障的主要特征，SKE既考虑了峭度对于冲击特征的敏感性，也考虑了包络谱熵对于周期信号的敏感性，σ 用于平衡两者的变化率。当σ ＜1 时，SKE随着周期性冲击分量的增强而逐渐增加。

2 方法流程

基于DEVMD方法的直升机行星轮系故障监测方法流程如下。

①采用加速度传感器采集原始振动信号。

②采用OGS算法进行前置降噪。

③基于DEVMD方法对故障敏感信号进行提取。

a.采用DEVMD方法对信号进行模态分解，得到BIMF分量。

b.从分解的BIMF分量1 ～K 中提取故障敏感信号分量。

④对提取的故障敏感信号分量进行包络谱分析。

⑤提取SKE故障指示因子进行故障监测。

⑥输出故障监测结果。

3 实验验证

3.1 实验设计

实验采用直升机行星轮系实验平台采集的样本数据进行验证，采用安装在齿圈壳体处的加速度传感器进行信号采集，采样频率为10 kHz，如图2 所示。故障模式涵盖正常状态和3 种不同裂纹长度的故障状态，如图3 所示。

图2 直升机行星轮系实验平台

图3 正常状态与3种不同裂纹长度的故障状态

3.2 实验结果分析

3.2.1 基于OGS算法的前置降噪效果评估

信号降噪前后波形如图4 所示。由图4 中的消噪效果可见，默认阈值降噪与全局阈值降噪在消除噪声的同时也大幅削减了高频信号，保留了低频信号；高频系数降噪利用尺度向量与阈值向量对高频系数进行阈值处理后重构降噪，在消除噪声的同时也削减了信号幅值。相比小波阈值降噪，信号通过OGS算法进行前置降噪后，大幅值的冲击信号更加突出，小幅值且分散的信号得到了收缩，降低了信号中噪声的幅值，整体提高了信噪比。

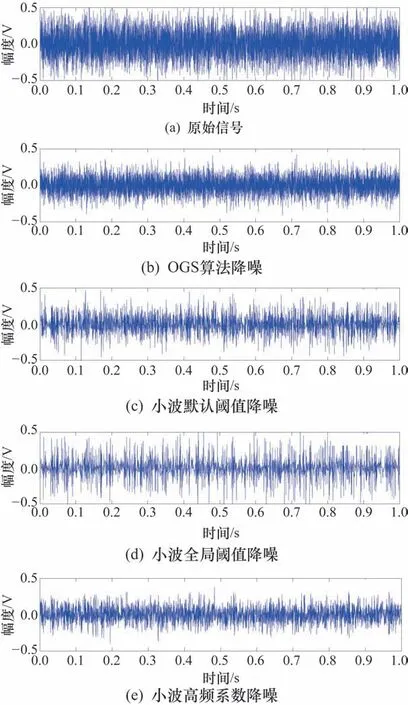
图4 信号降噪前后波形

为了定量评价本文方法的降噪效果，采用信噪比（Signal-to-Noise Ratio，SNR）与均方根误差（Root-Mean Square Error，RMSE）作为评价指标，结果如表1所示。由表1 可见，与小波各阈值降噪方法相比，OGS算法降噪SNR最大，RMSE 最小，说明基于OGS算法的前置降噪更适用于这种具有成组稀疏特性的信号形式，其对噪声的滤除和对原有信号的保持效果更优。

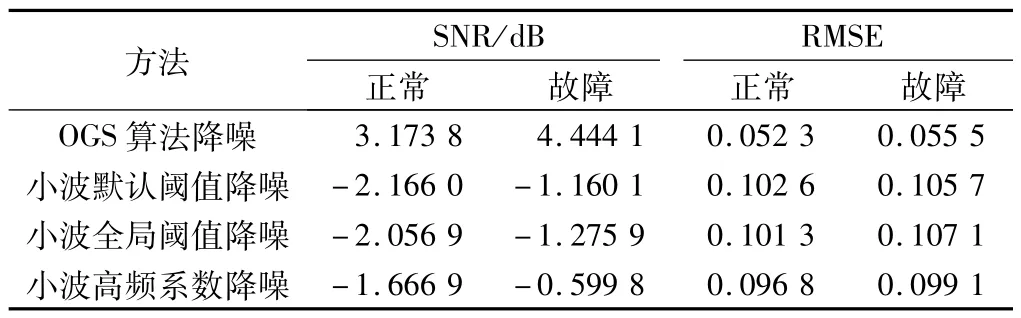
表1 OGS算法与小波各阈值降噪效果对比

3.2.2 基于DEVMD 方法的故障敏感信号分量提取效果评估

对OGS 算法前置降噪后的信号进行DEVMD 分解，根据经验值，带宽因子δ选择为5 倍太阳轮旋转频率，采用滑动平均功率谱密度极值点确定的模态数量K为5，中心频率｛｝＝｛5fib，fm，2fm，3fm，fsr｝。图5 分别为故障状态（太阳轮齿根裂纹）下，DEVMD 分解的各BIMF分量的频谱分布。由图5 可见，DEVMD方法准确地将信号分解为以主要齿轮部件的啮合频率或其倍频为中心频率的调制信号分量，中心频率分别为输入锥齿轮旋转频率5 倍频、行星传动轮系啮合频率及其2 倍频、3 倍频和二级减速齿轮啮合频率。由此可见，DEVMD方法有效地将各齿轮部件啮合振动形成的模态信号进行了分离，消除了齿轮部件啮合振动信号之间的耦合干扰，有利于单独对各齿轮部件的健康状态进行识别。

图5 故障状态下各模态分量的频谱分布

故障状态下，用DEVMD 方法将信号分解为主旋翼轴、输入锥齿轮、液压泵传动齿轮等各旋转频率及倍频成分组成的BIMF分量1、行星传动轮系一阶啮合频率及其边频成分组成的BIMF分量2、行星传动轮系二阶啮合频率及其边频成分组成的BIMF分量3、二级减速齿轮一阶啮合频率及其边频成分组成的BIMF分量4、行星传动轮系三阶啮合频率及其边频成分组成的BIMF分量5，如图6 所示。

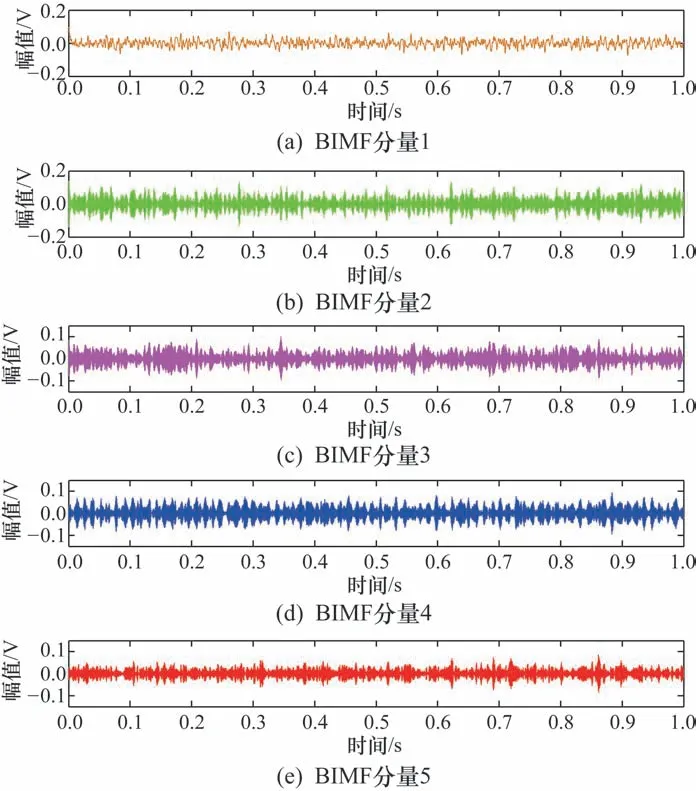
图6 故障状态下用DEVMD方法分解的BIMF分量

3.2.3 基于峭度-包络谱熵的故障监测效果评估

按照故障敏感信号分量提取准则，从BIMF 分量中提取中心频率分别为行星传动轮系啮合频率、其2倍频和3 倍频的BIMF信号分量2、分量3 与分量5 作为故障敏感信号分量，故障模式下各故障敏感信号分量的冲击成分幅值相比正常模式均有所增强。故障敏感信号分量在正常状态与故障状态下的包络谱如图7所示，与正常状态相比，故障状态下包络谱中主要峰值谱线的幅值出现了较大幅度的增强，说明了行星传动轮系齿轮故障的存在。

图7 故障敏感信号分量的包络谱

计算正常状态与不同故障状态下故障敏感信号分量的SKE，如表2 所示。由表2 可见，在所有故障敏感信号分量中，BIMF分量2 的SKE在故障状态下最大，且与正常状态相比变化最大，不同裂纹长度对应的SKE不同，且随着故障程度增加（裂纹长度增大），SKE相应增大，从而实现故障监测。

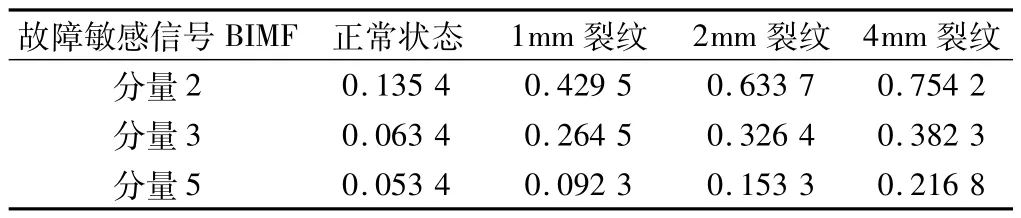
表2 故障敏感信号分量的SKE

3.3 实验结果对比

将本文方法与对比方法，即组合小波阈值滤波、EMD方法信号分解和归一化峭度值作为故障指示因子的故障监测方法进行对比，如图8 所示。由图8 可见，本文方法的故障指示因子在正常与故障状态下幅度变化的指示性和对应不同故障程度的趋势性都优于对比方法，体现了实验方法在直升机行星传动轮系故障监测中的优异性能。

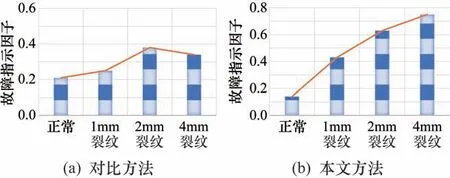
图8 DEVMD与对比方法的实验结果

4 结束语

针对直升机行星轮系复杂信号背景下故障特征的提取难题，提出了一种新的直升机行星轮系故障监测方法，该方法首先集成了OGS算法作为前置滤波对背景噪声进行抑制，然后通过DEVMD 方法对滤波信号进行分解并提取故障敏感信号分量，最后从故障敏感信号分量中提取SKE作为故障指示因子，实现了对直升机行星传动轮系的故障监测。采用直升机行星传动轮系实验平台的正常状态与3 种不同故障程度状态进行了本文方法的效果评估，并将评估结果与常用的其他方法进行了对比，验证了本文方法的有效性，解决了复杂信号背景下直升机行星轮系的故障监测难题。