深部煤炭流态化开采装备自主行走机构多缸推进同步控制
2024-04-08鲍久圣李玥锋赵少迪王忠宾葛世荣
鲍久圣 ,李玥锋 ,周 恒 ,阴 妍 ,赵少迪 ,王忠宾 ,葛世荣
(1.中国矿业大学 机电工程学院, 江苏 徐州 221116;2.中国矿业大学 深地资源流态化开采前沿科学研究中心, 江苏 徐州 221008;3.中国矿业大学(北京)机械与电气工程学院, 北京 100083)
0 引 言
2022 年我国煤炭产量为45.6 亿t,比2021 年增长10.5%[1],仍占据较大比例。然而,经过几十年大规模开采,露天矿以及浅煤层的煤炭资源已经被逐步开采殆尽,浅部资源正趋于枯竭[2–3]。研究表明,在现有技术条件下井工开采的极限深度约为1 500 m[4],因此突破煤炭开采方式和开采极限深度,向深部要资源已成为必然选择和重大需求[5]。2016 年以来,谢和平院士团队[6–7]创新提出了深地资源流态化开采科学构想,该技术以现有全断面硬岩掘进机技术为先导,采用多功能盾构式结构的设备,实现煤炭采选充、电气热一体化开采和原位转化。流态化开采设备由采掘舱、流态化转化舱、产能输出舱和充填舱等多部分组成[8],多舱协同工作是实现煤炭原位开采、分选、转化、填充和运输的技术前提。然而,由于流态化开采系统舱体繁多、体积庞大,如何解决多舱体装备系统在深地条件下的自主行走和协同推进是目前亟待解决的关键基础问题之一。
深地流态化开采系统借鉴敞开式全断面硬岩隧道掘进机(TBM)掘进技术[9],采用多缸协同作业的方式推进,为了实现盾构式多舱开采装备在深部地质条件下的直线掘进这一目标,需对各舱体间的多个液压缸同步推进控制问题进行研究。目前,国内外学者在此领域已开展了一些研究,例如:YANG等[10]提出一种基于PID 算法的压力和速度双闭环耦合控制的盾构机液压缸同步控制策略,通过试验表明两个液压缸同步误差保持在3 mm 以内;薛召等[11]提出了一种双缸同步控制策略,采用PID 结合模糊单神经元的方式,并进行仿真和试验,结果表明双缸同步误差在±3.3 mm 以内;徐莉萍等[12]提出了一种偏差耦合同步控制结合PID 算法的控制方法,并通过仿真进行验证,结果表明双缸之间的同步误差小于1.5 mm;XU 等[13]提出了一种基于径向基函数(RBF)网络自适应滑模控制的主从同步控制策略,提高了三液压缸同步动作的效果;SANATI 等[14]提出了一种负载力和同步误差反馈的交叉耦合同步方法,使整个系统的非线性及不确定因素得到了很好的抑制,同时提高了系统的控制精度;卢子帅等[15]将相邻交叉耦合与自抗扰控制相结合,仿真结果表明该策略同步控制效果良好且加快了系统的响应速度。然而,现有研究多集中于双缸同步控制,且多采用传统的主从控制和偏差耦合控制等控制方法,对于三缸及以上的多液压缸同步控制,其结构和控制系统都较为复杂,同步控制难度大,目前相关研究较少,针对深地复杂环境下的多缸同步控制研究则未开展。
深地岩体在“三高一扰动”的影响下,会出现大变形、强流变等特征,并且在地球内动力的作用下不同尺度的岩体岩石在不同时间和不同空间发生稳态/非稳态的演化[16],形成复杂的地质格局,如大尺度的均匀特质的岩石层、大尺度岩土突变的岩石层、小尺度非均匀特质的地质层。这些复杂的地质特征会导致开采设备在不同位置受到不同的地质约束,使得多缸同步控制系统的不同部分受到不同的阻力,产生振动、位移突变等现象,进而影响整个设备的运动平衡。鉴于此,针对深部流态化开采装备多缸同步推进控制需求,分析了多种不同的多缸闭环同步控制方法的优缺点,提出了一种均值耦合同步控制方法结合自抗扰控制器的多缸同步控制策略,并通过仿真和试验验证了其同步性和稳定性。
1 深部煤炭流态化开采装备增阻迈步式自主行走机构设计
深部煤炭流态化开采系统的结构原理如图1 所示,通过多个舱体的协同作业实现流态化开采与原位转化,舱体间采用液压缸实现推进功能,并在舱与舱之间设置有柔性伸缩保护罩,防止煤层塌方卡死设备。

图1 深地流态化开采系统示意Fig.1 Schematic diagram of deep ground fluidized mining system
1.1 自主行走机构结构设计
针对深部流态化开采系统的盾构式多舱开采装备结构特点,设计了一种增阻迈步式自主行走机构[17]。由图1 可知,最少3 个舱体即可实现装备的自主行走功能,所以选取采掘舱、流态转化舱及产能输出舱3 个具有特色的舱体作为设计研究对象,如图2 所示。自主行走机构是由采掘舱、转化舱、输出舱、前/后推进液压缸和增阻系统组成的,每个舱体之间采用液压缸铰接,通过液压缸之间的协同推进实现设备前行、转向等功能。借鉴敞开式TBM 行进原理,在转化舱和输出舱上方布置有增阻液系统,采用增阻液压缸伸出顶板代替“撑靴”作用,实现舱体固定功能。

图2 增阻迈步式自主行走机构结构Fig.2 Structural diagram of increased resistance walking equipment for autonomous walking
1.2 自主行走机构行走原理
自主行走机构的推进液压缸与增阻液压缸协同工作推动各舱增阻迈步式前进,整个迈步过程原理如图3 所示,①转化舱上布置的增阻液压缸活塞顶出抵在煤层上,转化舱与煤层锁定;②转化舱上的4个前推进液压缸活塞顶出,推动采掘舱前行进行煤炭开采,实现头部采掘舱行进;③转化舱增阻液压缸活塞缩回,解除转化舱和煤层的锁定,尾部舱的增阻液压缸活塞顶出抵在煤层上,尾部舱与煤层锁定;④ 4 个前推进液压缸活塞缩回,4 个后推进液压缸活塞顶出,通过“前拉后顶”实现转化舱行进;⑤尾部舱增阻液压缸活塞缩回,解除尾部舱与煤层的锁定,转化舱上的增阻液压缸活塞再次顶出抵在煤层上,转化舱再次与煤层锁定;⑥后推进液压缸缩回,拉动尾部舱行进。

图3 增阻迈步式自主行走原理Fig.3 Principle of increasing resistance and stepping autonomous walking
2 自主行走机构多缸推进系统同步控制策略设计及仿真
为了解决深部煤炭流态化开采装备自主行走机构在推进过程中的多液压缸同步控制问题,对推进液压系统建模仿真,对比了所提出的控制策略与3种常用控制策略的综合性能,并对其鲁棒性进行优化。
2.1 液压推进系统建模
液压推进系统如图4 所示,在采掘舱和转化舱之间布置4 个液压缸作为前推进装置,在转化舱和输出舱布置4 个液压缸为后推进装置。

图4 液压推进系统原理Fig.4 Schematic diagram of hydraulic propulsion system
由恒压变量泵2 向前后推进系统的8 个液压缸提供恒定的液压压力,采用比例调速阀4 控制液压缸活塞伸出缩回的速度,通过换向阀5 控制液压缸运动的方向。将位移传感器8 测量的液压缸6 伸缩时的位移信号进行微分,得到速度信号并将其反馈至控制器以实现液压系统的闭环控制。
由于前、后推进系统的液压油路完全相同,因此选择前推进系统进行仿真,同时因为换向阀、过滤器等原件对液压系统影响较小,所以对前推进系统的建模进行一定的简化处理,所建立的模型如图5 所示。

图5 推进系统仿真模型Fig.5 Propulsion system simulation model
2.2 多缸同步控制策略设计
当前多液压缸同步控制方法主要包括主从同步控制、相邻交叉耦合同步控制、偏差耦合同步控制等,并对以上3 种控制方法及提出的均值耦合同步控制方法进行分析。
1)主从同步控制。根据从动元件跟随不同主动元件耦合关系的不同,可将主从同步控制分成2 种形式,如图6a 所示为形式①,选择其中某个液压缸为主动元件,剩余液压缸为从动元件,从动液压缸跟随主动液压缸进行动作。如图6b 所示为形式②,后一个液压缸跟随前一个液压缸的运动进行动作。主从控制通过在增加各控制通道之间的耦合关系实现液压缸同步控制,然而主从控制是从动液压缸跟随主动液压缸进行动作,因此存在从动液压缸跟随滞后时延的现象。

图6 主从同步控制Fig.6 Master-slave synchronous control
2)相邻交叉耦合同步控制。相邻交叉耦合液压缸同步控制是使相邻的两个液压缸之间的动作存在耦合关系,其结构如图7 所示。图8 为相邻交叉耦合误差补偿器结构,将相邻通道2 的输出信号和相邻通道4 的输出信号与通道1 的输出信号进行比较,将差值送至补偿器并进行相加,作为反馈信号输入动作原件。然而非相邻之间的通道存在滞后现象,此外,相邻交叉耦合误差补偿器需要3 个输入信号,对于具有n个液压缸的相邻交叉耦合同步控制系统,则需要3n个控制器。
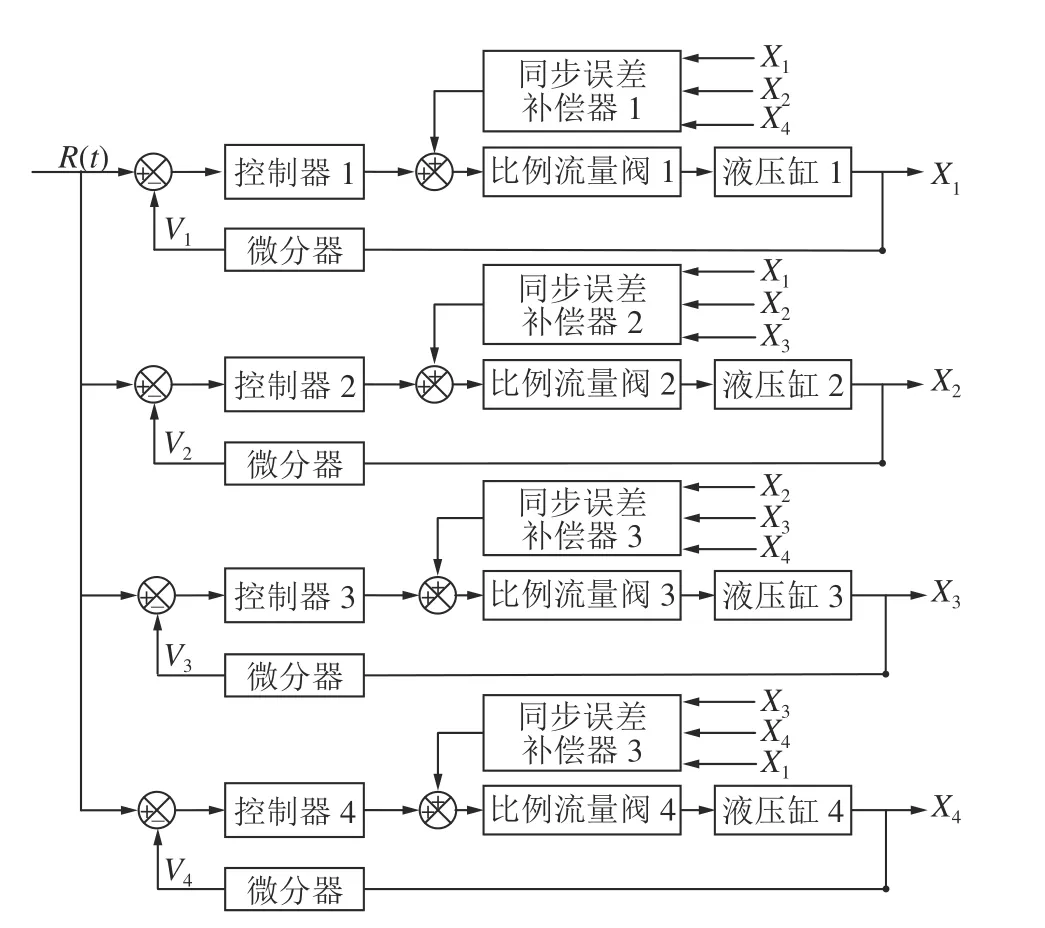
图7 相邻交叉耦合同步控制Fig.7 Adjacent cross-coupling synchronous control

图8 相邻交叉耦合误差补偿器结构Fig.8 Adjacent cross-coupling error compensator structure
3)偏差耦合同步控制。偏差耦合同步控制方法如图9 所示,偏差耦合同步控制是在并行同步控制的基础上加入位置误差补偿器,如图10 所示为偏差耦合误差补偿器结构,控制系统中每一个缸的位移信号均与通道1 的输出信号进行比较,将比较后的差值传送至误差补偿器,然后将所有补偿器的结果累加,形成通道1 液压缸的补偿器输出信号,反馈至控制器实现对通道1 的液压缸的偏差耦合同步控制。

图9 偏差耦合同步控制Fig.9 Deviation coupling synchronous control

图10 偏差耦合误差补偿器结构Fig.10 Structure of deviation coupling error compensator
误差补偿器考虑所有液压缸的运动状态,每一个液压缸位移信号都传送至误差补偿器,因此当一个通道的液压缸受到扰动导致活塞速度发生变化时,剩余液压缸立即进行跟随,该控制方法同步效果较好。然而偏差耦合系统需要n2个控制器。
4)均值耦合控制方法。以上3 种多缸同步闭环控制系统中,主从控制系统简单,然而存在从动件滞后的现象;相邻偏差耦合同步控制系统在相邻液压缸之间的同步效果较好,然而在非相邻的液压缸之间存在时延滞后现象;偏差耦合同步控制系统的液压缸同步效果较好,然而其存在运算量大,结构复杂,需要多个控制器等缺点。针对上述问题,提出了一种均值耦合同步控制方法,如图11 所示。

图11 多缸均值耦合同步控制Fig.11 Multi-cylinder mean coupled synchronous control
均值耦合控制是一种用于实现多通道液压系统同步控制的方法。通过计算所有液压缸位移信号进行平均计算,求得平均值,将平均值作为每个通道的同步误差补偿器的输入信号。该方法综合分析所有液压缸的运行状况,将两舱体之间4 个液压缸的移动量的平均值作为参考对象:
式中:Xm为参考模型输出位移;Xi为第i个液压缸的输出位移。
比例阀输入信号为
式中:ui为输入信号;G为速度环控制器输出增益;R(t)为输入信号;Vi为液压缸的输出速度;T为位置环同步误差补偿器输出增益。
从式(2)中可明显得出均值耦合同步控制算法整合了全部通道的液压缸的运行情况,每个通道中只需n个位置控制器和n个速度控制器,相较于上述2 种控制方法,大幅减少了同步控制方法所需的控制器数量,同时均值耦合同步控制方法在具备偏差耦合同步控制高精度的基础上,又克服了相邻交叉耦合控制中同步时延滞后的难题。
2.3 多缸同步推进控制仿真
对主从控制、相邻交叉耦合控制、偏差耦合控制以及均值耦合控制4 种同步控制方法进行仿真分析,对比其同步控制性能的优劣,将PID 算法融入均值耦合控制方法中,得到如图12 所示模型。
1)仿真工况设计。如图13 所示,按照地质特点的不同,将地下煤层工况分成3 类[18–20],即流态化开采设备会遇到3 类不同工况,第1 类:均匀工况,设备在地质均质的工况下开采前行,所有液压缸承受相同负载,但随着设备前进速度加大,设备驱动力也随之变大。第2 类:突变工况,设备在掘进过程中突然碰到形状不规则的硬岩,4 个液压缸承受不同时刻的变负载。第3 类:时变工况,设备在掘进过程中遇到复杂的地质特征,煤层中存在不同形貌、不同硬度、分布不均匀的硬岩,各个液压缸承受的外负载在时刻发生变化并在一定范围内波动,外部负载的时刻变化使液压阀的阀芯受到振动的影响,阀门开度难以控制,从而引起流量的波动,导致液压缸同步困难。
因目前尚无2 000 m 以深的煤层采掘数据实例,以锦屏水电站引水隧道工程作为依据[21],计算行走机构在不同工况下的驱动力,设置3 种工况的加载曲线如图14 所示。图14a 为在稳定地质环境下推进速度与驱动力关系,拟定仿真工况0~5 s 推进速度为1 mm/s,5~10 s 推进速度均匀增加,10 s 时推进速度达到2 mm/s。图14b 为突变工况时的模拟负载曲线,前2 s 内4 个液压缸承受2 000 kN 均匀外部载荷并保持不变,第2 秒时采掘舱在液压缸推进下,刀盘的局部位置切割到复杂地质的硬岩,导致一个液压缸承受的载荷突变为3 000 kN,另外3 个液压缸外部载荷保持不变,第4 秒时随着推进系统继续向前推进,采掘舱刀盘切割硬岩的区域变大,第2 个液压缸承受的外部载荷也突变到3 000 kN,随后的第6 秒及第8 秒,第3、第4 油缸所支撑的刀盘区域承受的外部载荷突变为3 000 kN,并保持不变;图14c展示了随机选取4 种在一定范围内波动的不同的白噪声,并乘上增益系数k形成的时变载荷,并将4 种不同的时变负载分别导入4 个液压缸的仿真模型,用以模拟设备的时变负载工况,时变负载模型如图15所示。

图14 不同地质工况加载曲线Fig.14 Loading curves for different geological conditions

图15 时变负载模型Fig.15 Time-varying load model
同时拟用各缸的最大位移同步误差作为评判标准:
式中,emax为最大位移同步误差。
2)均匀负载工况仿真。均匀负载工况下,由图16 可以看出当主从控制在刚启动时,因该控制方法存在滞后性,最大位移同步误差呈上升趋势,1.5 s时趋向稳定,误差保持在3.0×10-5m 左右,然而5 s后随着目标速度的增加,主从控制的最大位移同步误差也开始逐渐上升,这是由于主从控制不存在耦合关系,当目标速度发生变化时,各个液压缸之间发生滞后现象从而产生误差。其他3 种控制方法明显优于主从控制,并且在算法调整下,最大位移同步误差趋近于0 m。
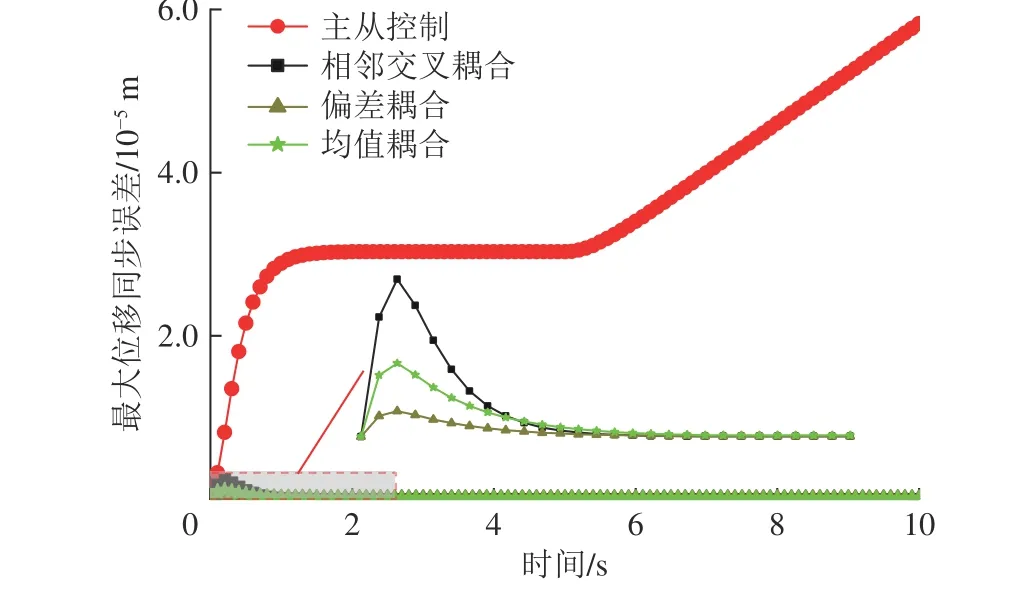
图16 均匀负载工况液压缸同步仿真结果Fig.16 Simulation results of hydraulic cylinder synchronization under uniform load conditions
3)突变负载工况仿真。突变负载工况下,由图17 可以看出主从控制的最大位移同步误差在2 、4、6、8 s 时由于各液压缸承受的外负载突变而产生较大波动,在其余3 种控制方法中,相邻交叉耦合同步控制下的最大位移同步误差大于偏差耦合控制和均值耦合控制,这是由于其非相邻的液压缸之间耦合存在滞后造成的,且3 种控制方法最大同步误差均保持在2.5×10-5m,具有较好的同步性能。

图17 突变负载工况液压缸同步仿真结果Fig.17 Simulation results of hydraulic cylinder synchronization under sudden load conditions
4)时变负载工况仿真。时变负载工况下,由图18 可以看出主从控制方法的最大位移同步误差在白噪声的时变负载下出现无规则的发散现象,抗干扰能力较弱。另外3 种同步控制方法最大位移同步误差趋于稳定保持在5×10-5m 以内,其中均值耦合控制方法最大同步误差保持在小范围内波动,且优于另外两种耦合控制方法,证明该同步控制方法具有更强的抗干扰能力,其同步性更加稳定。
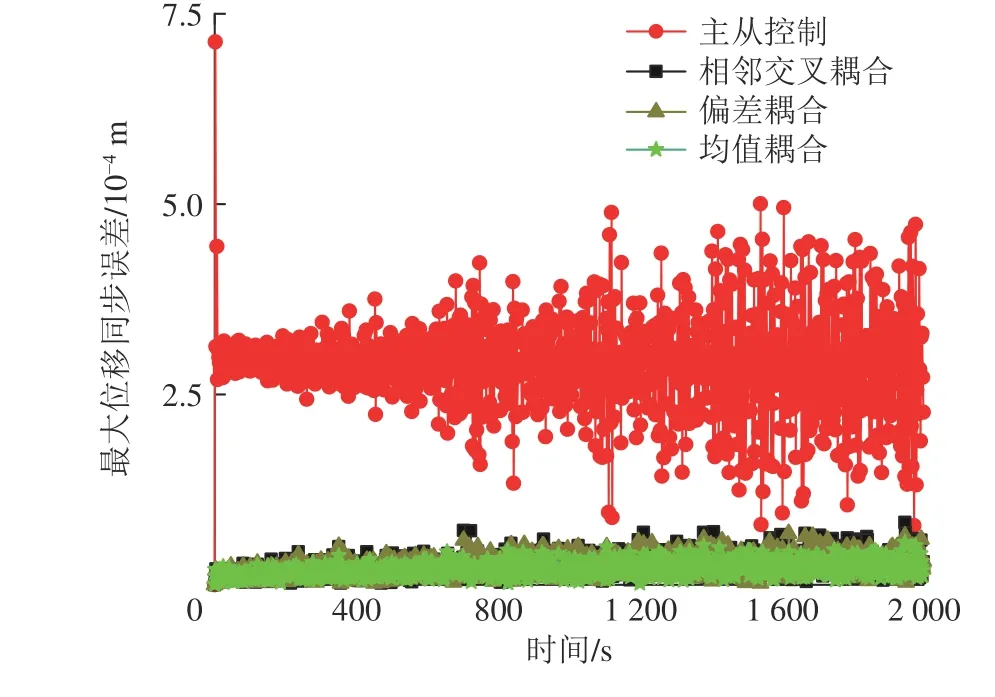
图18 时变负载液压缸同步仿真结果Fig.18 Synchronous simulation results of time-varying load hydraulic cylinder
2.4 多缸同步控制策略性能评价
对控制方法的评估不能仅限于精度,而应全面考虑真实工况中的运算速度、鲁棒性和成本等因素。为了更准确评估不同控制方法性能的优劣,提出了一种综合考虑各因素的评估方法—雷达图面积测评法。评分标准见表1,该方法结合了4 个指标,分别是精度、成本、速度和鲁棒性。这些指标通过最大位移同步误差、控制器数量、仿真时长及在时变负载下的仿真结果来体现。
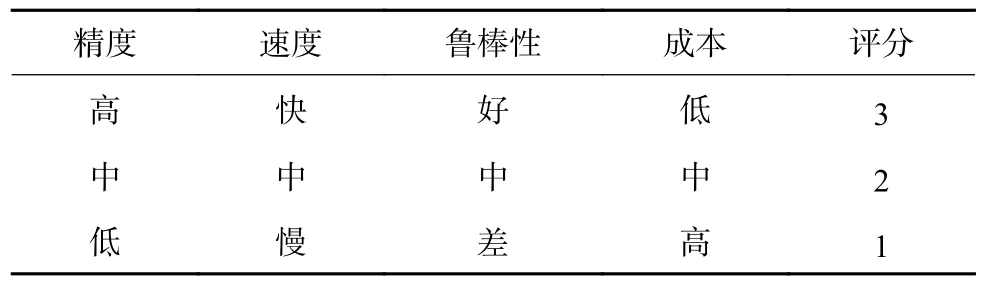
表1 控制策略评分标准Table 1 Control strategy evaluation criteria
绘制如图19 所示雷达图,其中四边形的面积越大表明控制策略的综合性能越优异。雷达图中主从控制、相邻交叉耦合、偏差耦合、均值耦合面积依次为12、16、10、20。其中均值耦合方法的面积最大,各项性能指标较为突出,所以选择均值耦合控制方法应用到流态化开采装备推进系统中。然而,从雷达图中发现4 种控制方法鲁棒性指标较差,这是因为经典PID 算法抗干扰能力不强造成的,因此采用现代控制理论中的自抗扰控制器提升控制方法的鲁棒性性能指标。
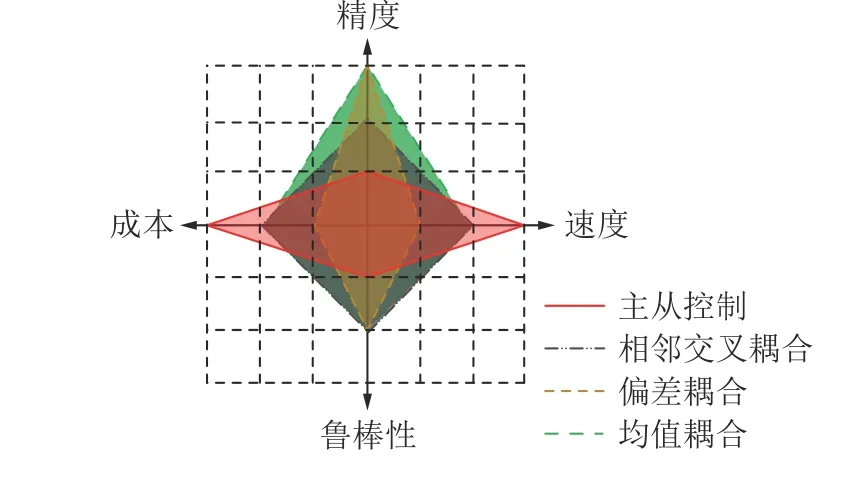
图19 4 种同步控制方法性能雷达图Fig.19 Performance radar chart of four synchronous control methods
3 基于ADRC 的均值耦合同步控制策略优化
前文同步仿真的控制器是基于PID 算法设计的,而PID 算法属于经典控制理论,是线性控制器,无法对系统内部的速度、加速度、非线性因素及系统外部扰动等进行调节控制,采用线性系统近似非线性系统导致控制了4 种同步控制方法的精度下降。而自抗扰控制器(ADRC) 属于现代控制理论的控制器,其能够估算和补偿液压同步控制系统中的非线性因素[22],有效应对系统的不确定性和变化,使得ADRC 在面对参数变化、外部扰动和模型不确定性等情况下依然能够保持较好的控制性能,并且与传统的控制设计方法不同,自抗扰控制器不要求精确的数学模型,通过将复杂系统转化为简单的积分串联型系统,使得控制结构更简化,提高了控制器的可实现性和可调节性,综上自抗扰控制器拥有强大的鲁棒性、抗干扰能力和快速响应性能。
3.1 模型建立
首先对推进系统进行分析,确定系统阶数。线性化的调速阀流量方程为
式中,QL为调速阀流量;kq为流量增益;xv为阀芯位移;kc为压力系数;pL为压力腔压力。
液压缸流量连续性方程[23]:
式中,AP为压力腔面积;xp为活塞位移;Vt为压缩容积;βe为弹性系数;Ctp为泄露系数。
液压缸平衡方程:
式中,Mt为总质量;Bp为黏性阻力系数;ke为负载弹性刚度;FL为负载力。
联立上述式(4)—式(6)3 个方程并对其进行拉氏变换得到液压系统的传递函数:
式中,kce为总压力系数。
上式为三阶系统,其结构复杂,系数繁多,运算量大,经典控制理论中的控制器设计难以满足需求。而自抗干扰控制器可将三阶系统中的三阶项和其他扰动转化为一个总扰动,最终将上式复杂的三阶线性系统转化为一阶线性系统[24–25]。
将式(7)以动态方程的形式改写为如下表达式:
将系统中的高阶项及未建模的扰动部分视为系统的总扰动:
则:
因此简化后的一阶系统控制器的控制结构如图20 所示。
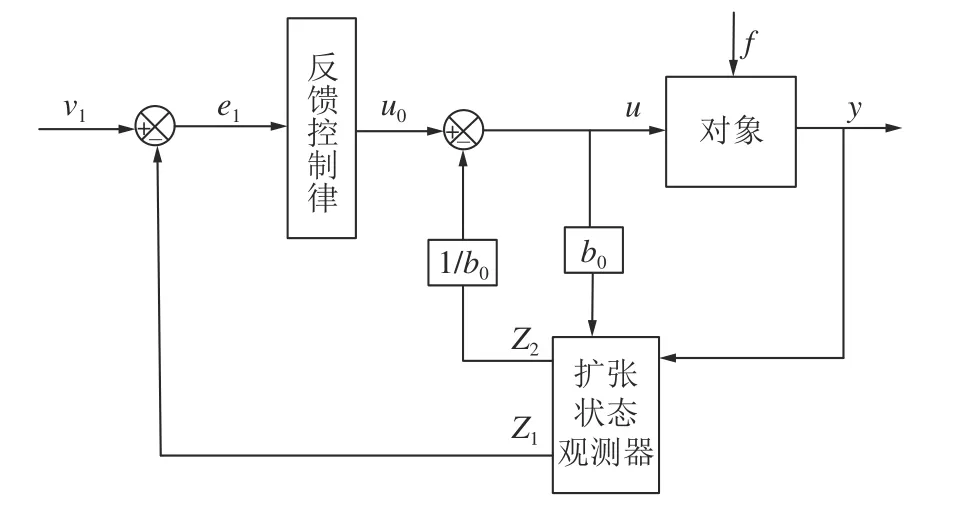
图20 一阶系统自抗扰控制结构Fig.20 Control structure of ADRC
非线性扩张状态观测器:
式中,z1,z2分别为v1和v2的观测信号;z1,z2为z1和z2的一阶导数;β01、β02为待整定系数;b0为控制矩阵;e1为观测误差;y为输出信号。
设计非线性反馈控制律:
式中,u0为反馈控制率的控制信号;β1为待整定系数;e为fal 的函数变量;δ为影响滤波效果的常数;a为0~1 之间的常数。
3.2 仿真试验
如图21 所示为在Simulink 仿真软件中建立的多液压缸的同步控制器模型,其核心是采用了前文所述的均值耦合控制方法和经典控制理论中的自抗扰控制器,并同时建立速度环和位置环进行反馈,以实现液压缸的同步控制。该完整的控制器模型由Sfunction 接口、位置耦合器、自抗扰控制器及同步误差补偿器组成。自抗扰控制器控制速度环,以降低系统受到的干扰,从而实现对液压缸活塞的速度同步控制。PI 控制器具有积分环节,可以积累误差并进行补偿,从而提高系统的抗干扰能力,因此位置环采用PI 控制器。整定参数见表2。

表2 ADRC 控制器参数Table 2 ADRC controller parameters

图21 Simulink 多缸同步控制器模型Fig.21 Simulink multi-cylinder synchronous controller model
如图22 所示为3 种工况下对ADRC 控制器和PID 控制器的多液压缸同步控制仿真结果。由图22a 和图22b 可以看出ADRC 控制器的仿真结果明显优于PID 控制器的同步控制效果。如图22c 所示,PID 控制器受时变负载的影响较大,其最大位移同步误差从最初的0.03 mm 扩大至0.05 mm,并且最大位移同步误差仍逐渐增大,而ADRC 控制器受时变负载影响较小,最大位移同步误差始终保持在0~0.04 mm 范围内波动。通过对3 种工况下的仿真结果表明,ADRC 控制器比PID 控制器具有更好的鲁棒性和抗干扰能力。
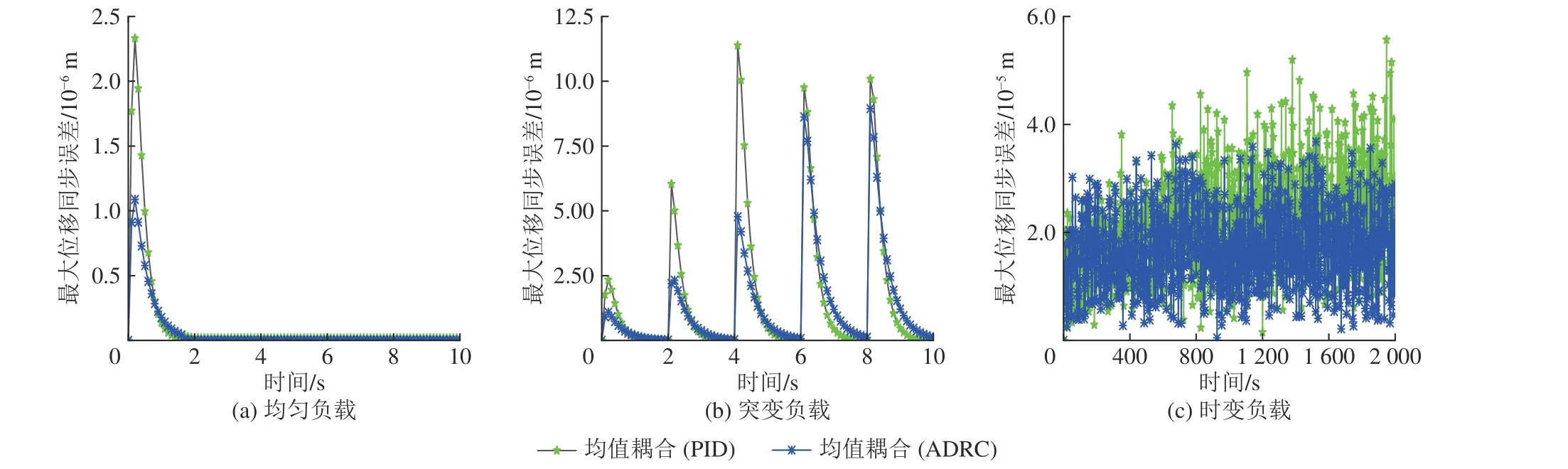
图22 联合仿真结果Fig.22 Co-simulation results
4 自主行走机构多缸同步控制试验
上文通过3 种不同工况下的仿真,确定了均值耦合同步控制为4 种同步控制方法中综合性能最为优异的方法,再对比PID 和ADRC 算法下均值耦合同步控制的结果,得出基于ADRC 算法的均值耦合同步控制策略优于PID 算法。为验证所提出自主行走机构和均值耦合同步控制方法结合自抗扰控制器的控制策略的可行性,研制了深部流态化开采装备自主行走机构试验台,并开展了多缸同步控制试验。
4.1 自主行走试验台
如图23a 所示为自主行走机构试验台,主要是由采掘舱、转化舱、输出舱3 个舱体组成,各舱体间布置4 个液压缸,通过液压缸推进舱体前行。采掘舱前布置有负载液压缸,通过调节两个液压缸的压力来模拟3 种不同工况。试验台测控软件调试界面如图23b 所示。

图23 自主行走机构试验台Fig.23 Autonomous walking mechanism test bench
试验过程中需要对运动元件在线监测,采用图24所示的压力传感器和位移传感器实时采集试验中的压力、位移等信号,并整合到上位机进行显示和存储。传感器参数见表3。

表3 传感器参数Table 3 Sensor parameters

图24 传感器选型Fig.24 Sensors selection
4.2 多缸同步控制试验
由于需进行不同工况负载下的同步试验,因此选取采掘舱与中间舱之间的液压缸进行同步控制试验。
4.2.1 不同速度下推进液压缸同步试验
1)均匀负载下的速度阶跃响应试验。调节负载液压缸压力为零,将试验台空载启动,首先设置推进液压缸以10 mm/s 的速度启动,待设备运行稳定后设定液压缸推进速度为20 mm/s。试验结果如图25所示,由图25a 可知控制系统在两次不同阶跃信号下响应迅速,速度波动均控制在5 mm/s 左右。由图25b 可知第1 次速度阶跃时最大位移同步误差在2.5 mm 以下,第2 次速度阶跃时最大位移同步误差在3 mm 以下,试验证明均匀负载的速度阶跃情况下控制系统同步性能较好。
2)均匀负载下的不同速度同步试验。推进系统在均匀负载时不同速度下最大位移同步误差如图26所示。观察图26 曲线发现,当初始速度为5 mm/s时,系统的最大位移同步误差在1.4 mm/s 上下波动,当初始速度为10 mm/s 时,系统的最大位移同步误差在2.5 mm/s 以内波动,当初始速度为15 mm/s时,系统的最大位移同步误差在2.6 mm/s 上下波动,当初始速度为20 mm/s 时,系统稳定后的最大位移同步误差在3 mm/s 上下波动。由此得出推论,多缸推进系统的最大位移同步误差和液压缸活塞的速度有关,给定的液压缸速度越快,最大位移同步误差越大。

图26 不同速度下最大位移同步误差曲线Fig.26 Maximum displacement synchronization error curve at different speeds
4.2.2 不同负载的下推进液压缸同步试验
1)突变负载同步响应试验。试验时首先调节左右两个负载液压缸压力为1 MPa,然后待液压缸稳定后,在第15 秒将左右负载液压缸的压力调至2 MPa,获得试验曲线如图27 所示。观察图27a 可知,当负载液压缸压力调节至2 MPa 时,4 个液压缸的速度发生突降,从10 mm/s 左右降至8 mm/s 左右,7 s 后速度恢复正常;观察图27b 可知,当负载发生变化时,4个液压缸的最大位移同步误差曲线从2 mm 突增至4 mm,随后曲线又恢复正常,保持在2 mm 左右波动。2)时变负载工况下推进液压缸同步试验。为模拟时变负载工况,在左右两个负载液压缸压力为2 MPa 的基础上,引入频率为0.1,振幅为1 MPa 的正弦信号,获得如图28 所示的试验曲线。由图28a 可知,4 个推进液压缸速度随正弦信号变化在8 mm 至12 mm 之间发生波动;由图28b 可知多缸最大位移同步误差波动范围在4 mm 以下。与突变负载相比,时变负载下的推进系统多液压缸速度和多液的压缸最大位移同步误差较大,然而其最大位移同步误差仍保持在一定范围内,具有较好的鲁棒性。

图27 突变负载试验结果Fig.27 Sudden load test results
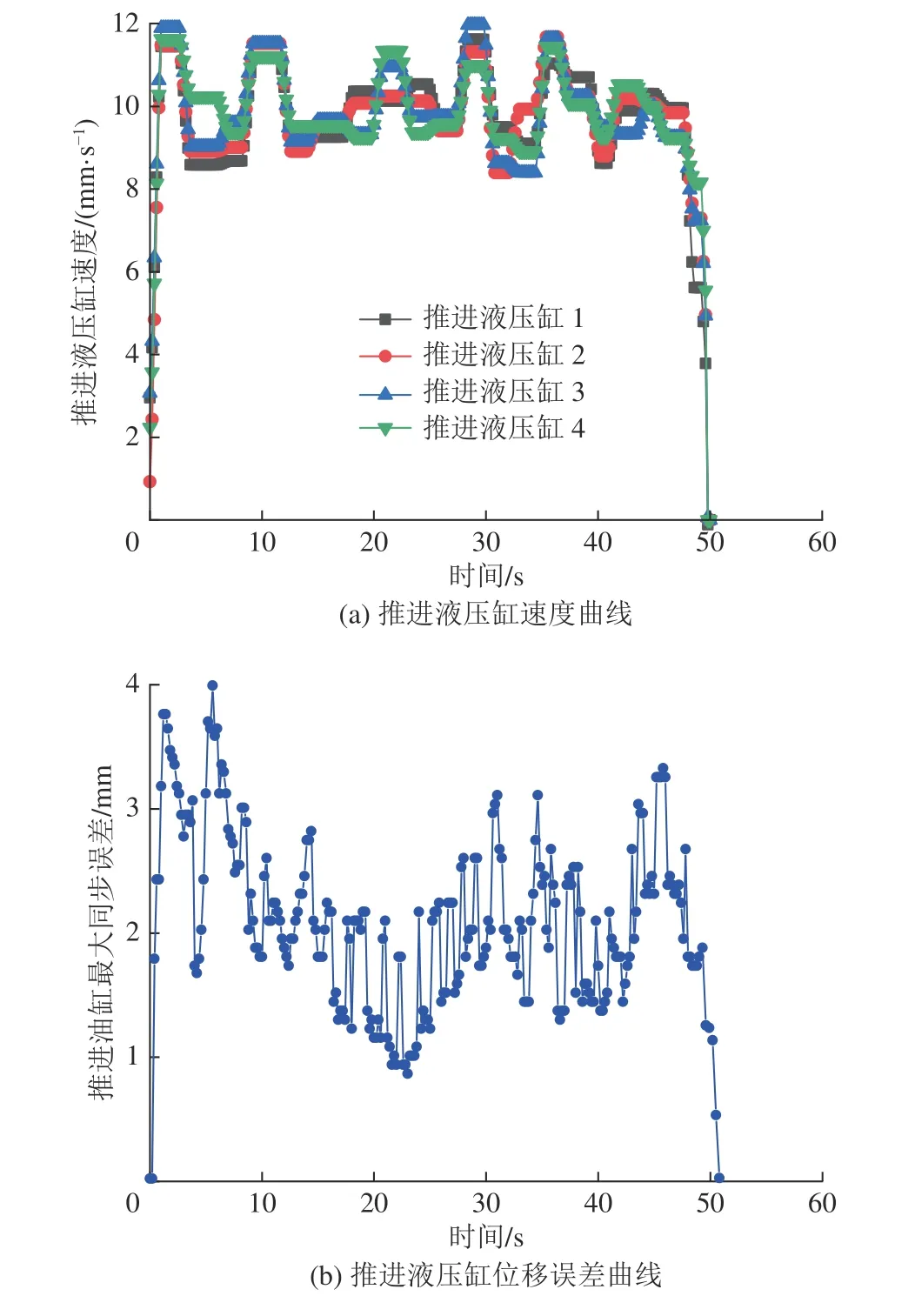
图28 时变载荷下多缸同步试验结果Fig.28 Result of multi-cylinder synchronous test under timevarying load
通过开展上述试验,分别从均匀负载下速度阶跃变化、推进系统不同速度以及突变负载和时变负载工况等多个方面,检测验证了基于ADRC 的均值耦合同步控制策略的优越性,试验结果表明该控制策略下最大同步位移误差均在5 mm 以下。
5 结 论
1)通过开展3 种工况下的仿真试验,构建4 种不同控制方法的雷达图面积评价模型,结果表明均值耦合控制方法的综合性能最优,但鲁棒性不强。
2)通过对比仿真分析发现,基于自抗扰控制的均值耦合控制策略比基于PID 控制的均值耦合控制策略鲁棒性更高。
3)通过自主研制自主行走机构试验台,验证了基于自抗扰控制的均值耦合控制策略的控制效果,结果表明所设计液压系统和提出的同步控制策略具有优异的同步性与鲁棒性。
