颗粒煤基质尺度计算新方法及应用

王 亮 ，李子威 ，郑思文 ，安丰华 ，赵 伟 ，吴淞玮

（1.中国矿业大学 安全工程学院, 江苏 徐州 221116；2.中国矿业大学 煤与瓦斯治理国家工程研究中心, 江苏 徐州 221116；3.河南理工大学安全科学与工程学院, 河南 焦作 454000；4.中国矿业大学（北京） 应急管理与安全工程学院, 北京 100083）

0 引 言

煤层瓦斯是与煤伴生、共生的气体，是一种高效清洁能源，属于非常规天然气。瓦斯运移可分为脱附、扩散、渗流3 个阶段，其中扩散与渗流的速度是决定瓦斯在煤体内流动快慢的关键，宏观上表现为抽采工程的效率[1-2]。煤是一种双重孔隙介质[3]，煤体被面割理和端割理切割为尺度不等的基质，基质内部含有大量以微孔和小孔为主的孔隙，煤中的瓦斯主要以微孔填充和单层吸附的形式保存在基质孔隙[4]。基质内孔隙提供了较大的比表面积，是吸附瓦斯赋存的主要场所，当瓦斯运移边界条件改变时，瓦斯分子首先从孔隙表面解吸，然后向裂隙扩散，再通过渗流运移出煤体。

基质间形成的裂隙尺度大且连通性好，是瓦斯渗流的主要通道。扩散发生在基质内部的孔隙中，抽采后期随浓度梯度下降，瓦斯运移出基质的阻力大，扩散的速率总体上比渗流速率低，因此在串联传质关系中，扩散是限制瓦斯抽采的主要传质形式[5]。瓦斯扩散受很多因素的影响，如气体压力、煤体温度和湿度等外部条件以及煤阶、破坏类型、煤的粒度等内在因素[6]，其中内在因素对煤体内部瓦斯运移的影响机理是研究的难点。颗粒煤的大小和不规则形状决定了瓦斯扩散路径的长短，在建立模型时将颗粒煤基质简化假设成规则球体是研究瓦斯运移的常用手段，而基质尺度就是其中的重要参数。此外，扩散系数为什么会随着粒径的增大而增高始终没有一致的答案。笔者认为这与颗粒煤粉化损伤过程的基质尺度有关。同一种未损伤煤体基质尺度是相同的，而不同程度粉化损伤样品的基质尺度认为是不一样的，这种差异性不仅改变了瓦斯扩散空间，同时还影响着扩散模型的假设与参数的选择。因此研究煤基质尺度对揭示煤的双重孔隙结构、丰富瓦斯流动理论有着重要意义。

多年来，在学者们的研究中，通过测试出煤不受有效应力和吸附变形等外界因素影响时的裂隙孔隙率 φf和渗透率k，可求出煤等效基质尺度，卢守青[7]通过该方法得到原生煤等效基质尺度为0.731 7 mm。ZHOU 等[8]利用测井数据获得中国沁水盆地东南部的无烟煤层结构特征，得到的等效基质尺度在0.39～0.67 mm。GUO 等[9]将煤的双孔隙结构简化为具有规则形状的几何形状，并将几何形状的尺寸看作煤基质和裂隙的等效尺度，考虑了煤的双孔隙结构、有效应力和基质吸附变形对煤渗透率的影响，提出了一种确定煤层渗透率的方法。近年来，煤基质的吸附膨胀变形成为研究的热点[10-14]。煤具有很大的比表面积，吸附瓦斯后，煤的表面能降低，基质发生膨胀，影响煤基质尺度。一些学者对煤解吸过程中的结构变形进行研究，得到了瓦斯流出煤体过程中基质的动态变化规律[15-16]，但没有对基质的尺度进行定量研究。LIU 等[17]在解释基质形状因子对瓦斯扩散量的影响时，将颗粒煤的粒径代替基质的大小进行计算，这一简化将导致结果存在较大误差，因此对基质尺度的定量研究是十分必要的。基质内部为扩散提供场所，外部连接着裂隙空间，为渗流提供瓦斯输入[4]，是煤中瓦斯2 大主要流动形式的重要载体。而对基质尺度的研究大多是从渗流的角度，通过渗透率来计算。有研究表明试验得到的表观扩散系数与表观渗透率在描述某一流体在多孔介质中传播时具有一致性[18]，但很少有人从扩散的角度，借助扩散系数对扩散和基质形态的关系进行分析。

笔者从扩散的角度，分析煤基质与裂隙的质量交换关系，通过颗粒煤解吸的动态过程求解基质形状因子，进而推算出颗粒煤等效基质尺度。该方法不仅从另一个角度提供了计算各种粒径下煤基尺度的方法，还对进一步研究扩散渗流关系，解释不同颗粒煤的扩散规律有着重要意义。

1 扩散基础理论

1.1 扩散模型

扩散系数是表征扩散能力的关键参数，主要反映扩散阻力的大小。通常采用实验室测定的方法获得煤中瓦斯的扩散系数，测试方法包括颗粒法、稳态法和互扩散法。单孔扩散模型常被用来求解煤粒瓦斯扩散系数[19-20]。经典的单孔扩散模型解析解如下：

式中：Qt为t时刻扩散总量，mL/g；Q∞为极限扩散量，mL/g；t为扩散时间，s；r0为煤颗粒瓦斯扩散半径，m；n为级数。

经典扩散模型中扩散系数D是一个定值，不能准确描述瓦斯扩散全过程，而本文需要得到各时刻点的瞬态参数，因此研究选用李志强等建立的指数式动扩散新模型[21]，新模型的基本假设为：①煤粒为各向同性的球体；②煤粒孔隙系统由多尺度、大小不一的非均质多级孔隙构成，从煤粒球体表面开始由表及里，孔隙由大到小逐级递减并连续分布；③瓦斯在多级孔隙中扩散时，仍符合连续介质力学假设。新模型提出扩散系数随时间的关系为

式中：D(t) 为动扩散系数，cm2；D0为t=0 时的初始扩散系数，cm2； β为动扩散系数的衰减系数，s-1。

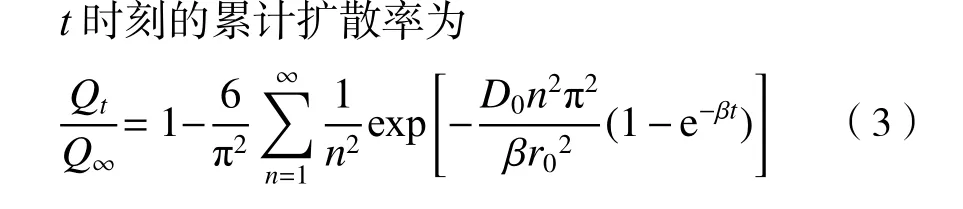
用新扩散模型对解吸试验结果进行拟合得到初始扩散系数D0和扩散系数衰减系数 β，进而可以得到时变扩散系数D(t)。

1.2 基质模型与基质形状因子

基质模型是对基质形态的描述，其中具有代表性的几何形态有球形、板形和圆柱形，如图1 所示，Pm为煤基质内部平均瓦斯压力，Pf为煤裂隙瓦斯压力。时变扩散模型将颗粒煤中瓦斯扩散单元看作球形[17]，因此研究选用球形基质模型来进行研究。

图1 基质与裂隙质量交换Fig.1 Matrix and fracture mass exchange

基质形状因子是与基质几何形状相关的一个特殊因子，它影响着煤储层中的气体运移和基质-裂隙中的流体交换。甲烷在煤的双重孔隙结构中的运移方式不同，因此在2 种体系中的运移速度也不同[22]。

由Fick 第一定律得到煤基质同裂隙间的质量交换公式[23-24]：

式中：QS为单位时间内单位体积煤中扩散的瓦斯量，kg/(s·m3)；J为质量通量，kg/(s·m2)；S为基质与裂隙质量交换面积，m2；V为基质体积，m3；D为瓦斯扩散系数，m2/s； σ为基质形状因子，m-2；C¯m为煤基质中气相瓦斯浓度，kg/m3；Cf为裂隙中的气相瓦斯浓度，kg/m3。

在煤基质与裂隙系统的质量交换公式中，基质形状因子 σ是一个非常重要的参数。形状因子反映了被裂隙切割的煤基质特性，既与煤基质的形状有关，也与基质内瓦斯扩散系数和质量浓度有关。

由式（4）可得形状因子：

同时形状因子满足[25]：

基质形状因子与基质体积V、基质与裂隙的质量交换面积S和扩散的特征距离L有关。本文将通过解吸试验动态过程数据对基质形状因子进行求解。以往的研究中通常使用吸附时间来求解基质形状因子，但考虑煤中瓦斯解吸过程缓慢，试验周期长，要准确记录解吸出63.2%的瓦斯较为困难[23]，且本文需要解吸过程中的瞬态数据，故选用式（5）来计算。

1.3 扩散特征距离

对球形基质模型来说，瓦斯的扩散是从基质中心往外扩散，因此球基质的半径即为扩散的特征距离，扩散特征距离L等于球形基质的半径R。图2 为扩散特征距离。基质球体的外表面积即为基质与裂隙质量交换面积S，基质体积V可通过球体积公式计算出来。由式（6）可得 σ =3/R2。

图2 扩散特征距离Fig.2 Methane diffusion pathway

基质形状因子与扩散特征距离和基质的几何形态有关。进而可得出球形基质半径的表达式，球形基质直径d可反映基质尺度的大小。

式中，基质形状因子 σ可通过颗粒煤的解吸试验数据求得。

1.4 基本假说

结合前三节给出的基础理论，研究提出以下基本假设，将依据以下假设进行分析：①煤基质为各向同性的球体。②煤基质内部孔隙系统由多尺度纳米级、大小不一的非均质多级孔隙构成，且分布均匀。③基质内扩散按照孔隙由大到小，扩散位置按照从基质外到内的顺序进行，受浓度梯度的驱动。④瓦斯在多级孔隙中扩散时遵从连续性原理，瓦斯解吸为等温条件下的解吸过程。⑤在短时间内的扩散过程看作是在稳态扩散条件下进行的。⑥颗粒煤内部瓦斯流动全部看作扩散，忽略大颗粒煤基质间的裂隙渗流。

从基本假设中可以看出颗粒煤解吸规律符合解吸带模型。随着瓦斯解吸时间的增长，瓦斯的解吸带在变小，扩散距离在增大，同一解吸带内扩散又按照孔隙由大到小依次进行的，整个过程的扩散阻力一直在增大。图3 为扇形解吸带模型。

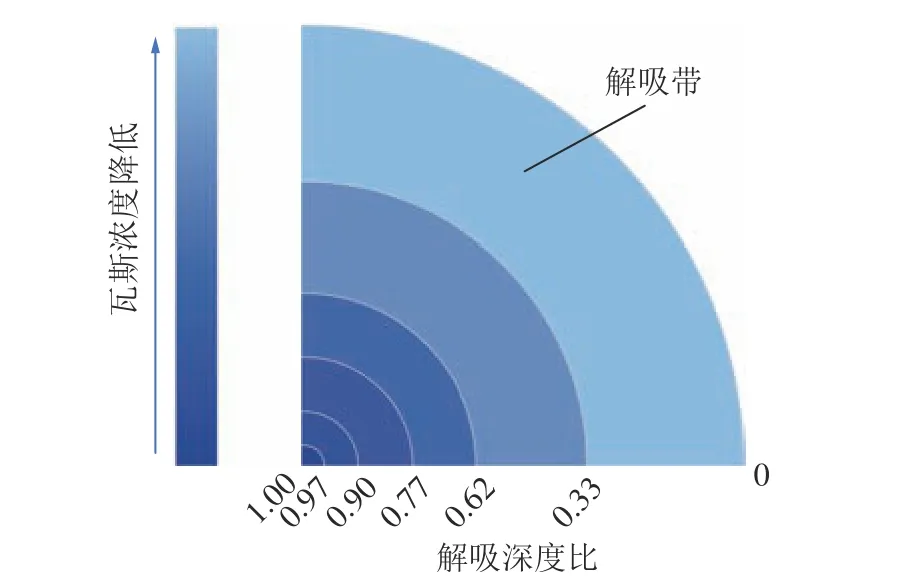
图3 解吸带模型[26]Fig.3 Desorption band model[26]

从图3 可以看出，随着解吸深度的增加，可解吸瓦斯量不断降低，扩散阻力却一直在增大，因此扩散系数随时间的延长会出现衰减。

2 时变扩散系数

通过开展煤样的等温吸附解吸试验，用时变扩散新模型对120 min 解吸数据进行拟合，可以得到扩散系数随时间的衰减函数。

2.1 煤粒瓦斯扩散试验

试验煤样选用来自贵州省普安县南部糯东矿的原生煤，记作ND，在中国矿业大学煤矿瓦斯治理国家工程研究中心进行粉碎和筛分，将煤制成了不同粒度（0.074～0.200、0.20～0.25、0.5～1.0、1～3 mm）进行物性参数和吸附常数等试验，测得煤样基本参数见表1。

表1 测试煤样基本信息Table 1 Basic information of tested coal sample

煤中甲烷扩散系数是对解吸试验得到的散点图进行拟合得到，所用试验仪器如图4 所示。对不同粒径范围煤样进行解吸试验，每组粒径取50 g放入煤样罐并加盖脱脂棉，封闭煤样罐后在60 ℃的水浴温度下连续抽真空24 h。往煤样罐中充入甲烷至所需压力，选择甲烷吸附平衡压力为1 MPa。在水浴30 ℃条件下吸附24 h 后认为已达到吸附平衡。达到吸附平衡后进行120 min 解吸试验。将得到的数据转为标况下的值，方便后面对比分析。

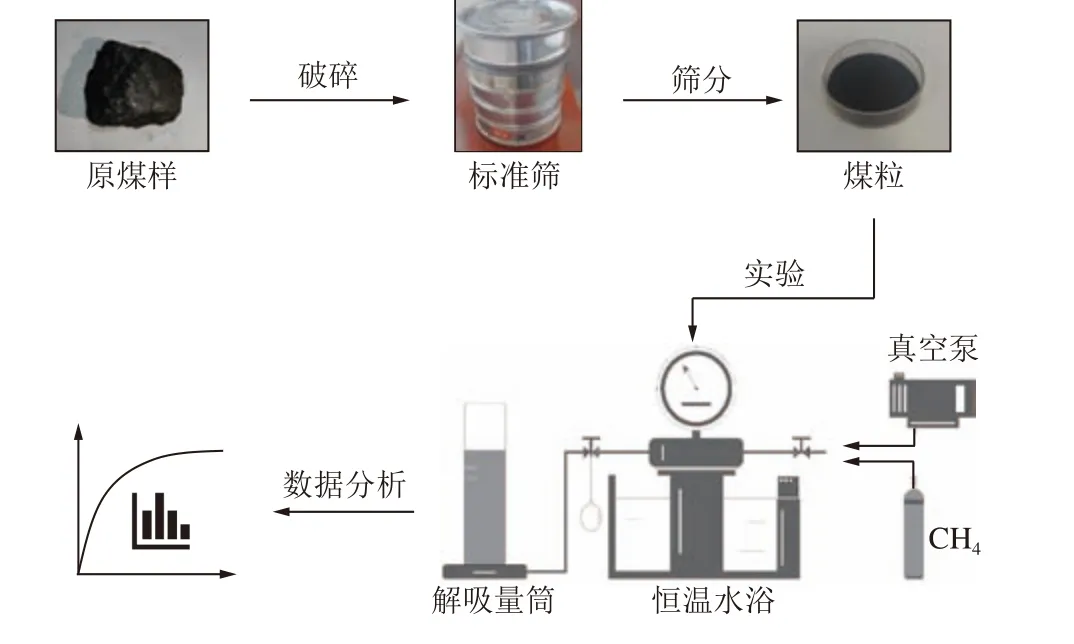
图4 试验装置及过程Fig.4 Experimental equipment and procedure

2.2 不同粒度煤时变扩散系数

利用指数式动扩散模型来对试验的3 组粒径解吸数据进行拟合，得到图5 所示的拟合曲线。

图5 扩散模型拟合结果Fig.5 Fitting results of diffusion mode

拟合数据见表2。3 种粒径的煤样解吸试验数据在动扩散模型的拟合下均有较高的拟合程度。相关系数都达到了0.98 以上。表明指数式动扩散模型可以很准确地描述扩散过程，进而证明其假设的科学性。

表2 动扩散拟合数据Table 2 Dynamic diffusion fitting data

扩散新模型认为扩散由表及里，孔隙由大到小逐级递减并连续分布的，从而表现出扩散系数随时间递减的关系。从基质角度来看，初始扩散系数D0是扩散刚开始瞬间的扩散系数，反映基质块最外层大孔隙中瓦斯扩散的难易。对于同一种煤样，煤颗粒越大，煤基质相对越完整，基质中大孔的破坏程度越低，初始的解吸带也比较大，甲烷的扩散阻力小，更容易进入裂隙中。小颗粒的煤，基质较小，大孔破坏程度高，初始解吸带较小，初始扩散系数较小，因此实验得到的初始扩散系数应与基质的破坏程度有关。

根据表2 的数据可以看出，初始扩散系数和扩散系数衰减系数都随粒径的增大而增大，与前人对时变扩散模型研究结果相同[27-29]，但前人未从基质层面对此进行解释。相比于0.074～0.200 mm 粒径的煤样，0.5～1.0 mm 和1～3 mm 粒径煤的初始扩散系数分别为 7.44×10-13m2/s 和 7.70×10-13m2/s，二者数值上较接近。而0.074～0.200 mm 煤样的初始扩散系数为 3.30×10-14m2/s，与其他2 组样相差很大。对于同一种煤样而言，其完整基质尺度是确定的，根据上面的分析可以推测0.5～1.0、1～3 mm 2 组大粒径煤样筛分破坏程度低，基本处于图6 中②～③的裂隙破坏阶段，基质保存相对完整，而0.074～0.200 mm粒径小于完整基质大小，到了③～④的基质破坏阶段，基质完整性遭到严重破坏，所以初始扩散系数大幅度降低。同样，扩散的极限粒径也可以从基质的角度来解释，当粒径增大到一定值后，原始的完整基质得到保留，瓦斯扩散是在同一尺度基质中进行的，因此再增大粒径对扩散系数的影响不显著。

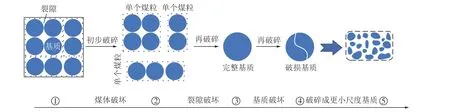
图6 煤破碎过程Fig.6 Coal crushing process

通过前文分析可以得知初始扩散系数D0与基质尺度有关，0.5～1.0 mm 和1～3 mm 粒径煤D0值接近，说明二者煤基质大小接近，可见在破碎筛分过程中，这2 种粒径的基质破坏程度低。而0.074～0.200 mm 煤样的初始扩散系数大幅度降低，说明在破碎筛分过程中其基质被破碎成更小的基质块，形成了更小尺度的基质。因此可以粗略推测ND 煤的原始完整基质尺度与0.5～1.0 mm 尺度相当且大于0.2 mm。下文通过基质形状因子进一步来计算不同颗粒煤的基质尺度。

3 基于扩散动态过程的等效基质尺度分析

3.1 瞬态参数计算

基于瞬态扩散求解煤基质尺度主要依据式（5）和式（6），通过基质形状因子的两种求解角度将煤基质的形状特征与扩散中瓦斯运移建立联系。从式中可以看出，新方法计算基质尺度所需参数可分为2 种，一种为试验获取，一种来源于基质模型的假设，见表3。

表3 新方法主要计算参数Table 3 Main calculation parameters of new method

其中时变扩散系数D(t)在2.2 节已经进行了求解。在1.3 节中对S、V、L进行了消参处理，而参数QS、C¯m和Cf的计算则是依据解吸试验的瞬态过程进行计算的，计算方法如下。

通过煤粒瓦斯解吸试验可得基质与裂隙间的质量交换速率QS[30]，根据式（8）求得：

式中：QS为单位体积煤基质同裂隙系统的质量交换率，kg/(m3·s)； Δt为读数时间间隔，s；Vt为煤样的总体积，m3；mt为t时刻瓦斯解吸总量，kg；mt+Δt为t+Δt时刻瓦斯解吸总量，kg。

裂隙中的瓦斯浓度与实验管路中的气相瓦斯浓度一致，可根据理想气体状态方程计算：

式中：Cf为裂隙中的气相瓦斯浓度，kg/m3；Mc为甲烷分子摩尔质量，kg/mol；R为理想气体常数，J/(mol·K)；T为煤体温度，K；Pf为气相瓦斯压力，MPa。

根据等压面原理，管路中的气相瓦斯压力可根据下式计算：

式中：Pa为大气压力，MPa；Pl为解吸量筒内液柱压力（ 9.81hw），MPa；Pw为水的饱和蒸气压，MPa。由于试验过程中量筒内液柱高度随时间降低，因此Cf也是关于时间的变量。

对于煤基质内部的平均瓦斯浓度的计算，下面给出了方法：将质量守恒方程应用于煤基质瓦斯扩散，基质瓦斯质量的总变化量即为扩散出来的总瓦斯量，单位体积煤基质中的瓦斯质量mm可根据朗格缪尔方程和理想气体状态方程进行计算：

式中：VL为朗格缪尔体积，m3/kg；PL为朗格缪尔压力，MPa； ρc为煤的视密度，kg/m3；VM为气体摩尔体积，0.022 4 m3/mol； ϕm为基质孔隙率，%。

初始时刻单位体积煤基质中瓦斯质量m0为

式中：P0为基质内游离瓦斯初始压力，本文为1 MPa。这是一个关于Pm的一元二次方程，通过MATLAB软件计算各个时刻下Pm在0～1 MPa 的根可以得到煤基质内游离瓦斯在t时刻的瓦斯压力Pm(t)。

然后通过理想气体状态方程可以得到时间t时基质内游离瓦斯浓度：

式中：C¯m(t)为t时刻煤基质中平均瓦斯浓度，kg/m3。

根据上文计算方法即可得到式（5）和式（6）在解吸各个时刻下的计算参数，下面只需要确定合适的时刻对应的值就可以求解颗粒煤基质尺度。

3.2 基质形状因子变化规律

按照3.1 节中介绍的数据计算方法得到3 种粒径试验条件下基质形状因子随时间的瞬态变化过程，如图7 所示。针对基质形状因子在不同时间段随时间的变化规律的不同，将解吸时间划分为3 个分区。在解吸初期，即0～1 000 s，形状因子随时间有个急剧下降的过程，在1 000～3 000 s 呈现缓慢下降的规律，3 000 s 之后趋于稳定。

图7 形状因子变化规律Fig.7 Variation pattern of shape factor

从纵坐标基质形状因子的数量级上可以看出，0.5～1.0 mm 与1～3 mm 煤样的解吸实验初期基质因子分别在 6×108m-2和 1.8×108m-2附近，属于同一数量级，而0.074～0.2 mm 粒径的初期基质形状因子将近 2.4×1010m-2，远大于其他2 个粒度，高出两个数量级。

基质形状因子反映了基质的几何形状，同时还与扩散的特征距离有关，CHENG[31]首次提出时变形状因子可以用式（6）来描述。扩散初期，基质外部瓦斯进入裂隙，在基质外部卸压区和内部未卸压区之间形成了浓度差，进而引起扩散效应逐渐往基质内部进行，瓦斯流出基质的特征距离就越来越长，即L的值在逐渐增大，如图8 所示。与此同时，由于基质的吸附膨胀特性，在瓦斯扩散出基质的同时会伴随基质的收缩。对于球形基质，可用式（15）表示为

由于扩散过程基质收缩，所以球形基质的半径R(t)随着时间的延长而缓慢减小，瓦斯流动特征距离L(t) 随时间延长而增大。在扩散前中期，R(t)的变化并不大，对基质形状因子产生影响的主要是瓦斯特征流动距离，流动特征距离的增大表现为图7 所示的基质形状因子在前中期的幂函数下降规律。随着扩散的进行，基质内部的浓度差值越来越小，瓦斯的流动也趋于平缓，基质-裂隙的质量交换系统逐渐达到拟稳态，L(t) 的变化不明显，近似可以看作L(t)=R，此时吸附态与游离态瓦斯的相互转换趋于平衡，R(t)也基本不变，从而导致式（15）的分母基本不变，形状因子的值也趋于稳定。

笔者选择基质的半径R作为扩散特征距离L，即认为瓦斯在煤基质中扩散的直线距离为基质半径长度。从基质扩散的动态过程来看，在扩散初期，基质外层瓦斯扩散的特征距离未达到R，扩散后期瓦斯的扩散特征距离接近基质半径R，在数值上表现为基质形状因子到扩散后期趋于稳定。一方面为了确保扩散特征距离尽可能接近R，另一方面为了减小吸附变形因素影响，选择3 000 s 后稳定形状因子的均值σ作为瓦斯扩散特征距离为R时的基质形状因子。

3.3 颗粒煤等效基质尺度

得到基质形状因子的之后，即可通过式（7）得到基质尺度d的值，计算结果见表4。

表4 基质尺度计算结果Table 4 Calculated results of matrix scale

对于完整的煤来说，扩散是从煤基质中进行的，当煤体遭到破坏，甚至破坏了基质的完整性，那么扩散就会从小于完整基质尺度的基质碎块中扩散出来，这一现象上文已通过初始扩散系数表现出来。因此，按照煤粒解吸实验计算出的基质尺度结果一定是小于实验粒径的。

通过表4 的数据可以看出，每组煤样的计算结果均小于煤颗粒大小。同样，0.074～0.200 mm 煤样计算的结果为0.059 mm，与其他2 组不在同一数量级。而0.5～1.0、1～3 mm 计算结果分别是0.287、0.457 mm，二者接近且在同一数量级，可知这2 个粒径范围筛分破坏程度低，与初始扩散系数的分析结果一致。通过表2 中的数据可以看到0.5～1.0 mm与1～3 mm 的时变扩散系数参数基本相当，说明1～3 mm 粒径煤样已接近ND 煤样扩散的极限粒径，再增大粒径对其扩散结果影响不大，其扩散规律与煤心处的扩散规律基本相同[32]，计算结果最能反映原始煤基质的等效尺度。因此ND 煤样的原始等效基质尺度计算结果接近0.457 mm；0.5～1.0 mm 颗粒煤样的平均等效基质尺度为0.287 mm；0.074～0.200 mm颗粒煤样的平均等效基质尺度为0.059 mm。

实验选取了3 种粒径的煤样，通过粒径与计算出的原始煤基质大小的对比可以发现，这3 种粒径煤样分别为小于完整基质的颗粒煤、与完整基质大小相当的颗粒煤以及远大于完整煤基质的颗粒煤。后两组基质未遭到严重破坏，相对完整，计算结果相近，这一结果进一步证明基于扩散效应求解基质尺度方法的准确性，该方法适用于不同颗粒大小的煤样基质尺度的计算，但若要得到煤样未受到筛分破坏的完整基质大小，尽可能选择块煤或大的颗粒煤进行实验。

4 K1 值的修正及损失量的计算优化

4.1 颗粒煤基质尺度的引入对K1 值的修正

钻屑瓦斯初期的解吸特性影响着煤层突出危险性，同时也是直接法计算瓦斯损失量的重要依据。井下常采用瓦斯解吸指标法预测采掘、石门揭煤工作面突出危险性，常用的瓦斯解吸指标有K1和 Δh2[33]，以钻屑瓦斯解吸指标K1值为例，其物理意义是钻屑瓦斯在第1 分钟的解吸量[34]。

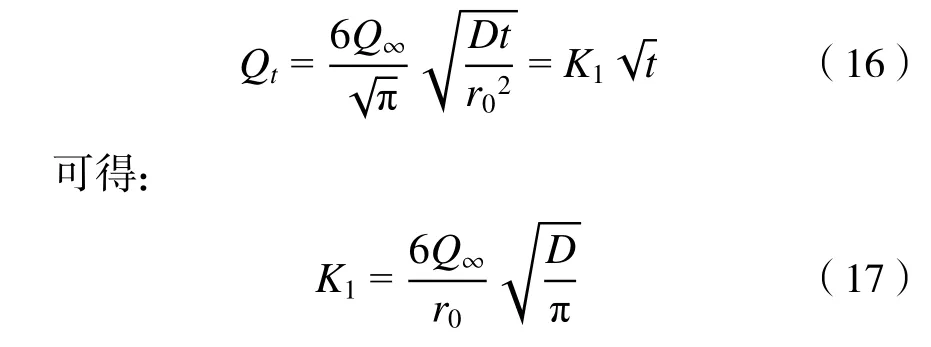
单孔扩散模型可简化为其中，r0定义为扩散距离，但众多学者将其假设为煤颗粒的半径r，这一假设使得计算结果偏小。扩散发生在煤基质内，基质与颗粒的大小是不同的，特别是对于构造煤来说，相同颗粒下，构造煤基质更小，这也是同粒径下构造煤的扩散率更大的原因[35-36]。因此r0的值应根据颗粒煤的等效基质尺来确定。假设煤样等效基质半径为r′，则修正后的解吸指标:

式中： α为修正系数，测定K1值通常选用1～3 mm 粒径，因此基质尺度越小，通过计算得到的修正系数α越大。

式中，D¯为0～t时间段内动扩散系数平均值，以下简称平均扩散系数。模型适用于初期的解吸曲线拟合，因此将式（17）中的扩散系数D看 作D(t)在第1 min 内的平均扩散系数，代入参数求解，进而得到r0不同取值下不同粒径煤样的K1值。

根据图9 所示结果可以看出，r0的2 种不同取值得到的K1值随粒径的变化所呈现出的规律是不同的。当r0=r时，K1值随粒径的减小有先增大再减小的趋势，无线性规律；当r0=r′时，计算结果增大了，K1值随粒径的减小而增大，按照粒径由大到小的顺序，依次增大了0.064、0.081、0.105 cm3/g，且增值随基质尺度的减小而增大，0.5～1.0 mm 和0.074～0.200 mm 粒径煤的K1值修正增量相比于1～3 mm 粒径煤的修正增量分别增大了26.56%，64.06%。根据解吸速率与粒径的关系可知，当粒径较小时，速率大，表现为初期解吸量大，K1值较大[2]，显然原本的计算模型在参数取值上存在很大误差，且误差会随着煤的粉化程度的增大而增大。因此当r0取值为颗粒煤基质半径时，钻屑瓦斯在第1 分钟的解吸量的计算结果与实测差值更小，修正后的K1值精度提高。

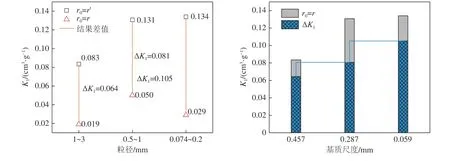
图9 钻屑瓦斯解吸指标K1 值计算Fig.9 Calculation of cuttings gas desorption index K1 value

图10 t 法确定解吸损失量修正前后对比Fig.10 t method to determine desorption loss before and after correction

随着我国矿井开采深度的不断增加，深部构造煤体呈现粉化结构特征，基质尺度变小，瓦斯流动速度加快，构造煤初始瓦斯解吸速度显著增大[37]。根据上文可知，K1值的计算误差随着基质尺度的变小而愈加明显。因此对K1值的修正将更有效的应用于深部构造煤的突出预测，为井下安全作业提供保障。

4.2 瓦斯损失量计算精准度分析

扩散模型参数的选择决定着瓦斯含量的计算精准度。通过利用颗粒煤基质半径替代煤颗粒半径实现对模型的修正将减小计算损失瓦斯量时的误差，这极大地影响了瓦斯资源含量的预测和对温室效应的评估。

5 结 论

1）时变扩散模型对解吸实验数据的拟合相关系数都达到了0.98 以上，可以准确得到扩散系数随时间的衰减规律。其中初始扩散系数反映基质外层大孔中瓦斯的扩散能力，与基质的形状大小有关，在一定程度上反映了煤基质的破坏程度。

2）煤基质形状因子具有时变性，扩散后期基质形状因子可准确反映基质形态。通过处理3 组粒径的实验数据，最终确定ND 三种颗粒煤的基质尺度分别为0.059、0.287、0.457 mm，随粒径的增大而增大，扩散极限粒径的存在是大颗粒煤基质的完整性的体现。

3）对比了K1值计算结果对煤颗粒大小和基质尺度的敏感性，结果表明代入基质半径进行计算得到的结果依次增大了0.064、0.081、0.105 cm3/g，呈现出的规律与实际煤样第1 分钟的解吸规律一致，对K1值有很好的修正效果，提高了直接法计算瓦斯损失量的精确性，对深部小基质的构造煤的突出预测具有指导意义。