同质区共享端元变异性的高光谱混合像元分解
2024-04-08王宁保文星屈克文冯伟
王宁,保文星*,屈克文*,冯伟
(1.北方民族大学 计算机科学与工程学院,宁夏 银川 750021;2.西安电子科技大学 电子工程学院,陕西 西安 710071)
1 引言
高光谱遥感图像包含着丰富的光谱信息和空间信息,已经广泛应用于资源勘探、灾害预警、国家安全、城市建设等诸多领域[1]。因为高光谱图像的空间分辨率一般较低,而地物的分布比较复杂,图像中一个像元体现出来多种地物的混合特征,这阻碍了以像元为单位的图像处理算法的发展[2]。高光谱图像混合像元分解也称高光谱解混(Hyperspectral Unmixing,HU),它根据混合的光谱特征去反演真实的地物分布比例,对地物的空间分布进行更精细的解译[3]。混合像元分解将光谱图像分解为端元和与端元对应的丰度,端元为构成高光谱图像的基本地物,丰度为地物在某一混合区域中所占的比例[4]。端元提取算法主要包括:纯像元指数(Pixel Purity Index,PPI)[5]、内部最大体积法[6]和顶点成分分析(Vertex Component Analysis,VCA)[7]等。丰度估计的经典算法为同时考虑丰度非负并且和为一约束的全约束的最小二乘方法(Fully Constrained Least Squares,FCLS)[8]。丰度的稀疏性是丰度常见的特性,它说明高光谱图像每个像元中只含有少量的地物[9]。
端元的光谱由于照明条件或大气条件的差异及其他因素导致相同地物的光谱出现差异,出现“同物异谱”的现象,导致端元光谱出现变异性[10]。线性混合模型(Linear Mixing Model,LMM)中的一个隐含的假设是在一幅图像中每一种材料通常由一个单独的光谱特征表示,认为总的光谱曲线是各个地物的光谱曲线按照其占比线性叠加[11]。从物理意义上来说,不能用单一的端元光谱曲线来进行混合像元分解,这也是LMM 的一个缺陷[12]。由于大部分解混算法都是迭代求解端元和丰度,如果忽略端元的光谱变异性,会导致在解混的过程中传播错误的建模误差,从而影响解混结果[13]。
相同地物选取多个端元光谱参与到混合像元分解中,可以有效处理端元的变异性。使用多端元解混中经典的算法有多端元光谱混合分析法(Multiple Endmember Spectral Mixture Algorithm,MESMA)[14]、光谱束解混法[15]及局部解混法[16],这些算法本质上在图像的不同空间位置上允许选用不同的端元进行解混。而基于统计模型的方法利用先验概率知识求解端元的分布,主要包括基于正态模型的(Normal Compositional Model,NCM)方法[17]、基于Bayesian 的方法[18]和基于β模型的(Bayesian Compositional Model,BCM)方法[19]。
在LMM 的基础上扩展的模型可以处理解混过程中端元变异性带来的不利影响,这些模型主要包括:扰动线性混合模型(Perturbed Linear Mixing Model,PLMM)[20]、扩展线性混合模型(Extended Linear Mixing Model,ELMM)[21]、广义线性混合模型(Generalized Linear Mixing Model,GLMM)[22]、增广线性混合模型(Augmented Linear Mixing Model,ALMM)[23]和缩放扰动线性混合模型(Scaled and Perturbed Linear Mixing Model,SPLMM)[24]。PLMM 改进传统的LMM,添加空间变化的扰动端元来描述端元的光谱变异性。ELMM 在解混中考虑空间信息和端元光谱变异性的同时,引入的尺度因子可以有效处理由光照条件引起的端元的光谱变异性。GLMM 认为不同波长可能会受到不均匀的影响,对每一个像元都引入一个与端元矩阵相同维度的矩阵与端元矩阵进行笛卡尔积运算,对端元施加更加精细的放缩。ALMM 使用共享的尺度因子,在一个像元中使用相同的尺度因子对所有的端元进行放缩,使用字典学习的策略构建尺度因子之外的光谱变异性,SPLMM 在PLMM 中添加共享尺度因子,一个像素中的所有端元共享相同的尺度因子。
在深度学习领域,一些处理端元光谱变异性的算法也取得较好的效果,经典算法主要包括:深度生成端元模型(Deep Generative Unmixing,DeepGUn)[25]、概率生成模型(Probabilistic Generative Model for Spectral Unmixing,PGMSU)[26]、空间光谱解混深度生成模型(Deep Generative Model for Spatial-Spectral Unmixing,DGMSSU)[27]和三维卷积神经网络(3D-Convolutional Neural Network,3D-CNN)[28]等。上述算法主要利用神经网络的非线性建模能力,联合空间信息与光谱信息,更好地拟合端元的分布情况。
照明条件的差异是引起端元变异性的一个重要因素,而尺度因子对光谱曲线的缩放能力已被证实可以有效处理由照明条件不同导致的端元变异性[13]。此外,高光谱图像中存在着大量的局部同质区,一个像元与其周围的像元有着相似的地物分布,端元的变异性也相对较小。针对PLMM 难以有效处理缩放效应造成的端元变异性这个问题,本文对PLMM 进行改进,提出了基于局部同质区共享端元变异性的解混算法(Shared Endmember Variability in Unmixing,SEVU),具体工作内容如下:
(1)在PLMM 中添加尺度因子以提高模型处理端元等比例变异性的能力,并提出一个针对尺度因子的正则项以约束端元缩放效应的强度;
(2)在解混的过程中引入超像素分割算法划分局部同质区域,在局部同质区内各个像元共享相同的变异端元,将端元变异性的尺度由像元级转变为超像素级;
(3)设计了基于交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)的解混算法以求解每个局部同质区的变异端元,并在一组合成数据集和两个真实数据集上进行实验,验证了算法的有效性。
2 高光谱解混方法
2.1 线性混合模型
2.1 线性混合模型
由于模型简单,物理意义明确,LMM是应用最为广泛的模型,它将高光谱图像看作由标准端元光谱矩阵与丰度比例矩阵的乘积。LMM中总的光谱曲线是由各个地物的光谱按照其占比线性叠加得到的。对于LMM,通常采用两个约束:丰度非负约束(Abundance Nonnegativity Constrained,ANC)和丰度和为一约束(Abundance Sum-to-one Constrained,ASC)。
LMM的向量形式为如公式(1)所示。在LMM中,Y=[y1|y2|…|yn]∈RL×N表示整幅图像,yn∈RL×1表示图像中的第n个像元,M∈RL×K表示端元,an∈RK×1表示yn对应丰度,rn∈RL×1表示第n个像元的重构误差,R=[r1|r2|…|rn]∈RL×N表示整幅图像的重构误差。
其中:L表示光谱波段数目,K表示端元数目,N表示这幅图像包含的像元个数。
2.2 扰动线性混合模型
扰动线性混合模型(PLMM)根据提取的端元可以被认为是参考端元的变化实例,改进LMM,添加逐像元的空间变化的扰动因子来描述端元的光谱变异性。PLMM如公式(2)所示,dMn∈RL×K表示yn对应的扰动端元矩阵。扰动端元的具体作用如图1(a)所示:

图1 不同因素对端元的影响Fig.1 Effect of different elements on endmembers
2.3 扩展线性混合模型
扩展线性混合模型(ELMM)在解混时用尺度因子来表示各种地物端元在所有像元中的变化,每种地物变异后的端元为对应参考端元矩阵乘一个尺度系数,这些尺度系数构成尺度因子矩阵。在ELMM中,Sn∈RK×K表示yn对应的尺度因子矩阵,是一个非负的对角矩阵。尺度因子可以对光谱曲线进行等比例放缩,它的具体作用如图1(b)所示:
3 改进算法
3.1 添加尺度因子的扰动线性混合模型
改进后的模型如公式(4)所示,Sn和dMn同时构造端元的变异性,Sn构造端元的等比例变异,而dMn构造端元的非等比例变异,其中第n个像元处的变异端元为MSn+dMn,尺度因子S和扰动端元dM对光谱曲线的影响如图1(c)所示。
端元矩阵和变异后的端元矩阵是非负的,需要对其进行非负约束,本算法也考虑丰度的物理意义,使用丰度非负约束(ANC)和丰度和为一约束(ASC)。综上,SEVU 算法的约束条件为:
公式(6)中α,β,γ,η是四个正则化参数,式(7)~式(10)分别为关于丰度、端元、扰动端元和尺度因子的四个正则化函数。
大多数混合像元中往往含有少量的地物种类,故针对丰度施加稀疏约束,通过公式(7)可以控制丰度的稀疏性:
因为目标函数的求解较为复杂,需要对多个变量进行迭代求解,有必要对端元进行合适约束以减小算法的解空间,所以使用端元之间的相互距离进行约束,如公式(8)所示:
其中:ek表示RK中正交基中的第k个向量,M=表示所有端元第l波段上的行向量,IK为维度为K的单位矩阵。
端元光谱变异性是有限的,变异后的光谱与原始光谱差距不会太大,为了使得模型具有更好的性能,有必要对变异性能量进行约束,其中对扰动端元的惩罚为:
当变异后光谱与原始光谱差值越小,端元变异性能量应当越小,受公式(9)的启发,对于尺度因子矩阵,本文提出针对等比例放缩的变异能量的惩罚项为:
3.2 超像素分割
PLMM 和ELMM 中端元变异性都是逐像元构建的,即一个像元对应着一个变异的端元,考虑到局部同质区中端元的变异性较小,所以在SEVU 算法中,一个局部同质区内多个相似的像元共享一个变异的端元。SEVU 算法使用超像素分割(Simple Linear Iterative Clustering,SLIC)[29]划分局部同质区。具体的像元间的相似度如公式(11)所示:
其中:ix,cx,iy,cy为两个像元的空间位置,Di,c是总的相似度,λ用于平衡光谱距离和空间距离的权重。其中SAM和SID计算如公式(12)和公式(13)所示,pil表示像元i在第l波段的辐射值:
对于划分出的任意一个超像素yslic在迭代求解时看作最小的单位,yslic=其中num为此超像素中包含的像元个数。所以对于整幅图像Y=[y1|y2|…|yn]∈RL×N,进行超像素变换,可得到变换后的图像YSLIC=[y1|y2|…|yq]∈RL×q,其中q为超像素的个数,因为q≪N,超像素变换可以看作高光谱图像的空间域的降维操作。同理,对于丰度矩阵A=[a1|a2|…|an]∈RK×N,按照上述变换规则,得到Aslic∈RK×q。
3.3 SEVU 算法
SEVU 算法在适度的局部同质区内共享一致的端元变异性,一块超像素代表一块局部同质区。给定一幅图像,超像素的块数影响同质区的大小,适度则表明这幅图像中超像素的大小并非固定的。共享端元变异性指在每一块超像素(同质区)内,所有像元使用相同的由尺度因子和扰动构造的变异端元求解最终的丰度,即SEVU 算法只构建同质区间的端元变异性,忽略同质区内的端元变异性。图2 为SEVU 算法示意图,首先输入高光谱图像,然后先由VCA 算法和FCLS算法对端元和丰度进行初始化,然后利用空间上下文信息将高光谱图像划分为若干个超像素,然后将超像素作为基本单位使用ADMM 求解变异后的各个局部同质区的端元,最后使用FCLS 算法并利用像元与超像素的隶属关系求解每个像元的丰度。
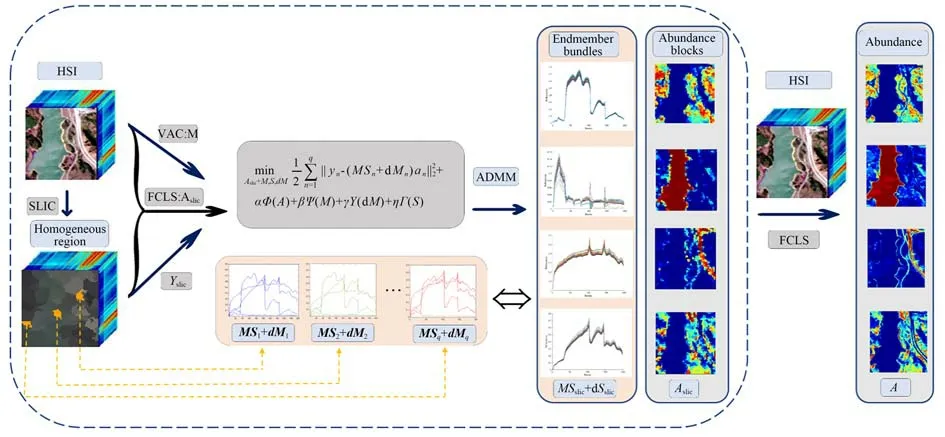
图2 SEVU 算法示意图Fig.2 Diagram of SEVU algorithm
3.4 算法求解
算法采用ADMM 进行求解。对于本模型中各个变量的求解,等价于最小化SEVU 算法的目标函数f(A,M,dM,S),使用ADMM 将目标函数的求解划分为四个子问题:丰度矩阵A,端元矩阵M,扰动端元矩阵dM,尺度因子矩阵S,然后采用拉格朗日乘子法(Lagrange Multiplier)求解各个子问题。
3.4.1 丰度
然后得到关于an的增广拉格朗日形式的函数,如公式(15)所示:
3.4.2 端元
P=[P1|P2|…|Pn],其中Pn表示按照如下规则将Sn中的对角元素转化为一个列向量:
3.4.3 扰动端元
3.4.4 尺度因子
对Sn求偏导数,令偏导数等于0,得到以Sn为自变量的西尔维斯特方程,如公式(31)所示,可以使用Matlab 中Sylvester 函数直接求解:
3.4.5 算法流程
SEVU 算法的流程如算法1 所示,首先,局部同质区的划分是依赖超像素分割算法SLIC 实现,超像素分割的块数q控制超像素的大小。然后利用ADMM 迭代求解每块超像素的变异端元,最后使用已求解的变异端元遍历超像素内的所有像元,使用FCLS 算法求得最终的丰度,其中停止条件为达到最大循环次数或目标函数接近收敛

4 实验结果与分析
4.1 实验数据集及评价指标
实验采用开源代码生成高光谱合成数据集(空间维度:50×50,光谱维度:198)[13],此数据集包含三个端元:植被(Vegetation),泥土(Soil)和水(Water)。端元光谱采用Simplified Illumination Model,Prospected-D Model,Hapke Model和Simple Atmospheric Compensation Model 来构建,丰度图像使用高斯随机场生成,丰度采用高斯随机场生成,然后基于LMM 逐像素生成高光谱图像,最后再将合成的图像添加20~40 dB 的高斯噪声。真实数据集使用解混中常用的数据集:Jasper Ridge 数据集(空间维度:100×100,光谱维度:198)和Cuprite 数据集(空间维度:150×270,光谱维度:188)。三个实验数据集的伪彩色图像及其端元光谱曲线如图3 所示(彩图见期刊电子版)。
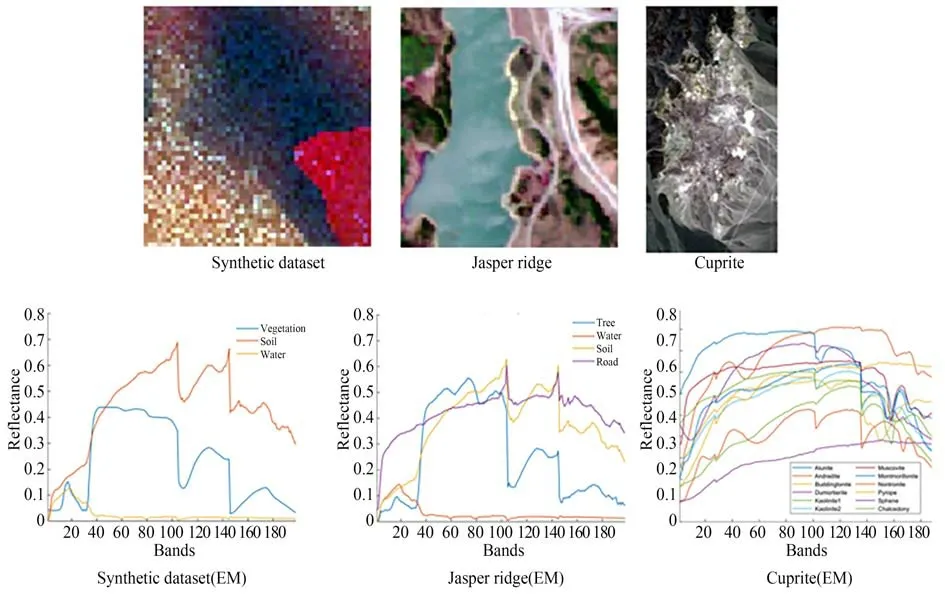
图3 数据集Fig.3 Datasets
评价指标包括平均端元光谱角距离(mean Spectral Angle Distance,mSAD)、丰度均方根误差(abundance Root Mean Square Error,aRMSE)和重构均方根误差(reconstruction overall Root Mean Square Error,rRMSE),以上三个评价指标均越低越好。需要说明,在端元变异场景下,需要估计每个像元的端元,但在真实数据集中端元的变异性是未知的,仅有一个可供参考的端元矩阵,所以计算真实数据集的端元提取精度时使用算法求解出的多个端元矩阵的平均值与真实数据集的端元矩阵计算mSAD[27]。
4.2 实验
为了验证SEVU 算法的有效性,实验使用的数据包括一组合成数据集和两个真实数据集,对比算法包括FCLS,SCLSU,PLMM,ELMM,GLMM,ALMM,所有实验均使用VCA 进行端元初始化。为了保证实验的公平性,在实验时已经对PLMM,ELMM,GLMM,ALMM 中的参数进行调优处理,均使用FCLS 进行丰度初始化。在接下来的所有实验中,高光谱图像中端元的数目已知,最终实验结果为10 次实验的平均值,最好的结果以粗体显示。
4.2.1 鲁棒性实验
为了验证算法的鲁棒性,实验一为不同噪声(20~40 dB)的场景下所有实验算法的对比实验。通过图4 可以看出,SEVU 算法在mSAD 和aRMSE 取得较好的效果。在端元估计中,ELMM 表现的效果最差,其次是GLMM,而添加扰动端元的PLMM 取得较好的效果,而FCLSU,SCLSU 和ALMM 没有求解端元;在丰度估计中,基于尺度因子的ELMM 和SCLSU 表现较差,而FCLSU 的效果较好;对于yRMSE,基于字典学习的ALMM 和使用更多尺度因子建模的GLMM 效果较好。随着信噪比的增加,所有算法的性能逐渐变强,由于超像素有降噪的作用,SEVU 算法在信噪比较低的情形下具有优秀的解混性能。

图4 信噪比对算法性能的影响Fig.4 Effect of signal-to-noise ratio on algorithm performance
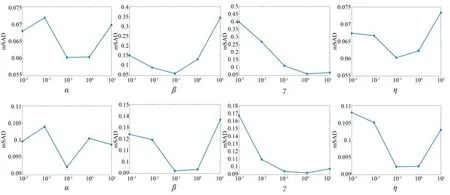
图5 参数对SEVU 算法性能的影响Fig.5 Effect of parameters on SEVU algorithm performance
4.2.2 参数实验
为了确定模型中的参数选择对混合像元分解精度的影响,实验二在Jasper Ridge 数据集上验证四个正则化参数的值对算法性能的影响,所有参数选择的数量级从10-3到101。图 5为α,β,γ,η的值对mSAD 和aRMSE的影响,mSAD 和aRMSE 对参数设定比较敏感,所以参数实验时主要考虑mSAD 和aRMSE。γ的值对算法性能最敏感,针对此数据集,γ=1,其余的参数等于0.1 时SEVU 算法性能较好。
4.2.3 超像素实验
在SEVU 算法中,超像素的块数是一个变量,代表着局部同质区划分的大小,同一幅图像,分割的块数越多,超像素包含的像元越少,表明同质区的同质性越强。超像素分割的块数影响SEVU 算法的精度和运行时间,实验数据集为:Jasper Ridge 数据集,实验时控制其他变量为:[α=0.1,β=0.1,γ=1,η=0.1]。图6 为此数据集分割块数后的平均光谱图像,结合表1 可以看出,yRMSE 始终与超像素块数成反比;算法运行时间与超像素块数呈正比。超像素分割的块数太少,从图像中使用的特征也少,求解的端元误差较大,故SEVU 算法的准确度很差;分割的块数越多,会忽视像元间的空间信息,难以取得较好的效果。当超像素分割块数为200~600 时,合理利用图像的空间信息,分割块数适中,SEVU 算法的性能较好。

表1 超像素块数对mSAD,aRMSE,yRMSE 的影响Tab.1 Effect of number of superpixel blocks on mSAD,aRMSE,yRMSE

图6 超像素分割后图像的块数Fig.6 Number of blocks in the image after superpixel segmentation
4.2.4 合成数据集实验
在合成数据集(30 dB)上超像素分割的块数为624,SEVU 算法的各个参数设定为:[α=1,β=0.01,γ=1,η=0.1]。通过表2可以看出,SEVU 算法在端元估计时准确性最高,对三种端元在平均光谱角距离上优于其他算法,其次是PLMM,GLMM,ELMM。总的来说,各个算法对水(Water)端元的处理能力最弱,说明考虑光谱变异性的解混算法均无法有效处理水这种弱信号端元的变异性。图7 显示了SEVU 构造的三个端元的光谱束,通过图8 和表3 可以看出,SEVU 求得的丰度更接近真实丰度,aRMSE更低。
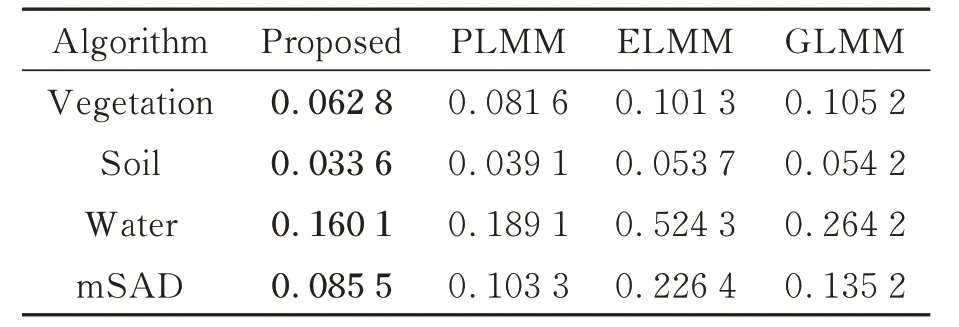
表2 各个算法在mSAD 上的评价结果(合成数据集SNR_30 dB)Tab.2 Evaluation results of each algorithm for mSAD(Synthetic dataset SNR_30 dB)

表3 各个算法在aRMSE 和yRMSE 上的评价结果(合成数据集 SNR_30 dB)Tab.3 Evaluation results of each algorithm for aRMSE and yRMSE(Synthetic dataset SNR_30 dB)
图7 SEVU 算法构造出的端元束(合成数据集 SNR_30 dB)Fig.7 Endmember bundles constructed by SEVU algorithm(Synthetic dataset SNR_30 dB)
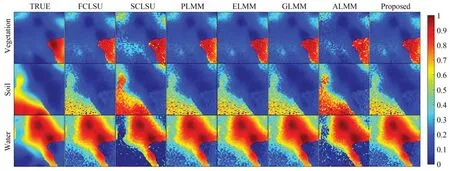
图8 各个算法估计的丰度图像(合成数据集 SNR_30 dB)Fig.8 Abundance estimated by each algorithm(Synthetic dataset SNR_30 dB)
4.2.5 真实数据集实验
对于Jasper Ridge 数据集,超像素分割块数:601块,参数设定为[α=0.1,β=0.1,γ=1,η=0.1]。图9 显示了SEVU 算法估计的四组相似的光谱束。通过表4 可以看出,除水之外其余端元的求解,SEVU 算法在mSAD 上均取得最好的效果;而对于水这种端元的求解,单独使用扰动端元的PLMM 效果最好,也反映扰动端元处理弱信号的优越性。在此数据集上,考虑端元变异性的算法求解的端元均比VCA 效果好,也说明在真实场景下考虑端元变异性的必要性。
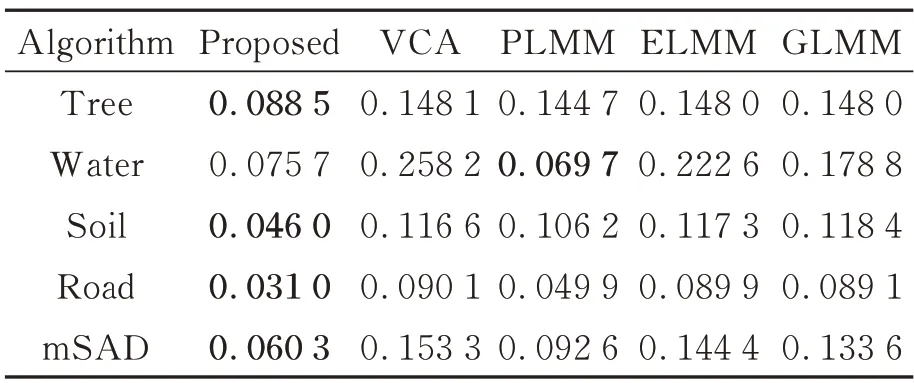
表4 各个算法在mSAD 上的评价结果(Jasper Ridge)Tab.4 Evaluation results of each algorithm for mSAD(Jasper Ridge)
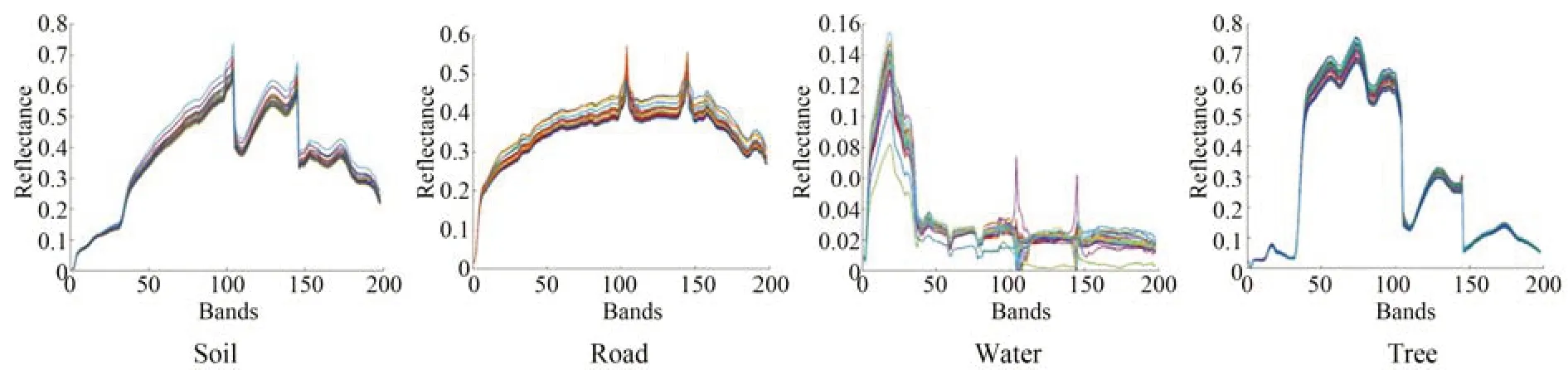
图9 SEVU 算法构造出的端元束(Jasper Ridge)Fig.9 Endmember bundles constructed by SEVU algorithm(Jasper Ridge)
结合图10 和表5 可以看出,SEVU 算法总体的丰度估计也是最优的,尤其对道路(Road)这种端元的求解的误差最低,进而对道路丰度的估计最接近真实值,说明在自然场景下基于局部同质区共享端元变异性两阶段分别求解端元块和丰度的可行性和有效性。

表5 各个算法在aRMSE 和yRMSE 上的评价结果(Jasper Ridge)Tab.5 Evaluation results of each algorithm for aRMSE and yRMSE(Jasper Ridge)
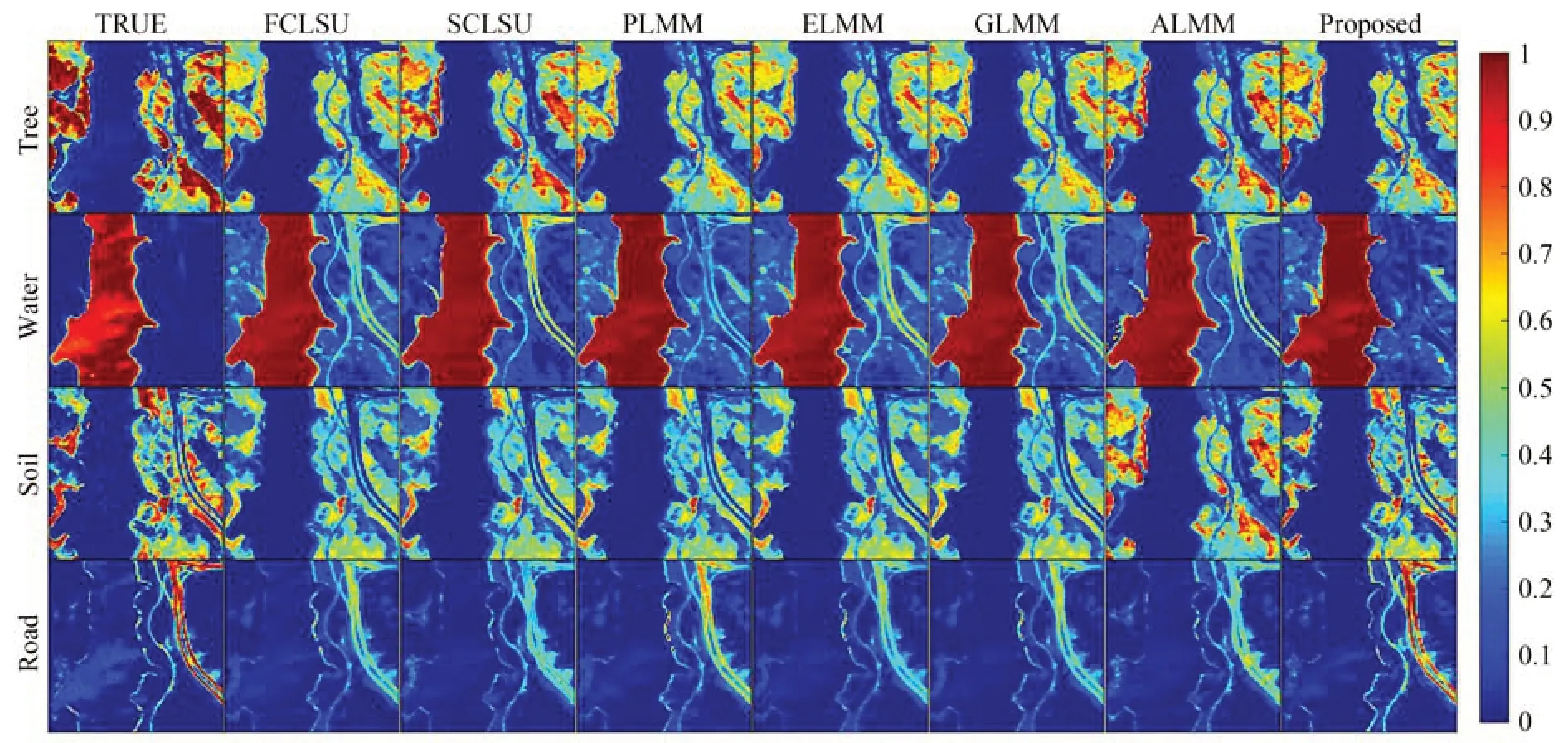
图10 各个算法估计的丰度(Jasper Ridge)Fig.10 Abundance estimated by each algorithm(Jasper Ridge)
对于Cuprite 数据集,超像素分割块数:10 124 块,参数设置:[α=0.01,β=1,γ=10,η=0.1]。图11 可以看出不同端元变异的强度是不同的,变异性弱的端元束几乎是单一端元的重复,表现出单一曲线的形态。本数据集极为复杂,因此超像素分割的块数较多,平均5 个像元构成一个超像素,对于本数据集,超像素主要起到降维的作用。观察表6 和表7 可以看出,SEVU 算法求解的mSAD 更加准确。所有算法在本数据集上的mSAD 较大,但各个算法之间的差异较小,大致在0.10~0.12 之间,也可以通过图12 看出各个算法求得的丰度图相似性较高。

表6 各个算法在yRMSE 上的评价结果(Cuprite)Tab.6 Evaluation results of each algorithm for yRMSE(Cuprite)
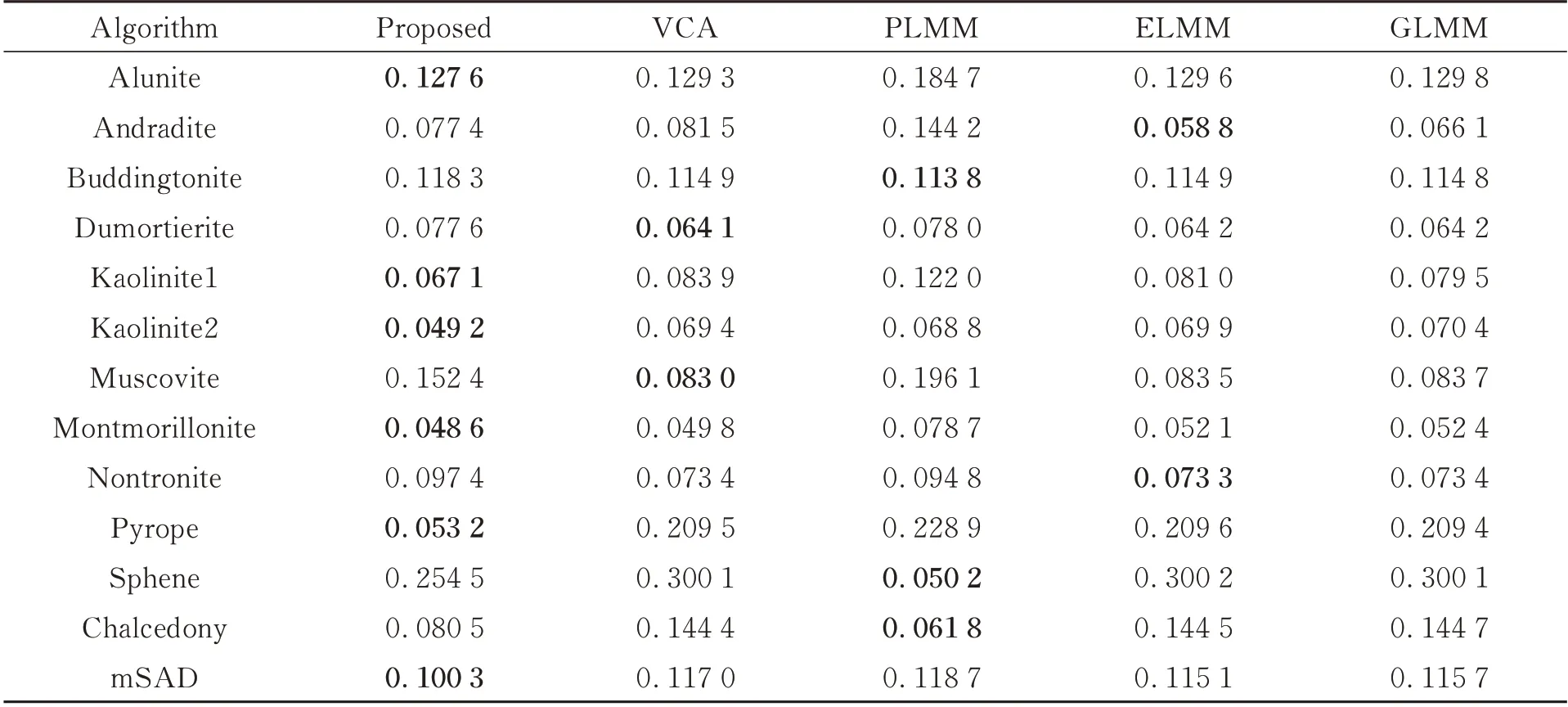
表7 各个算法在mSAD 上的评价结果(Cuprite)Tab.7 Evaluation results of each algorithm for mSAD(Cuprite)
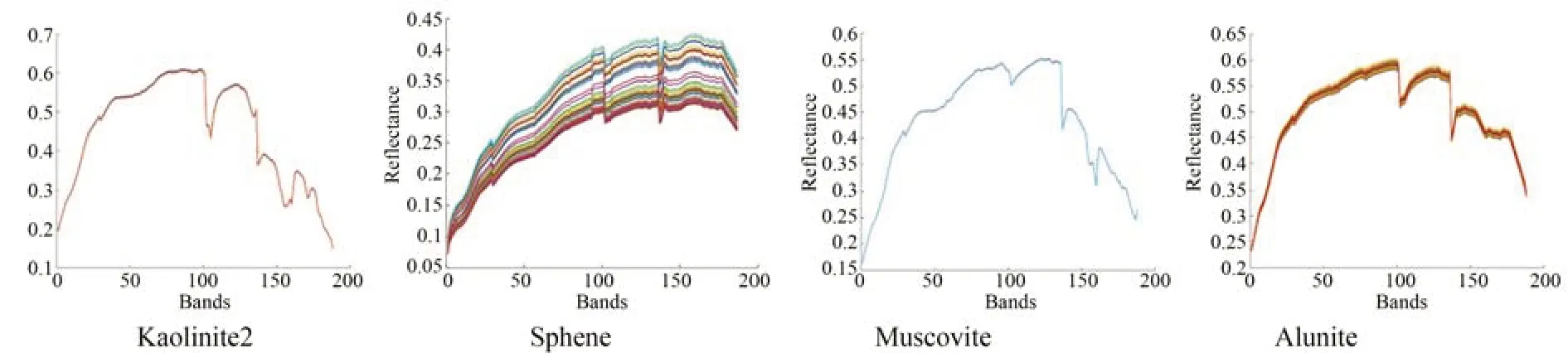
图11 SEVU 算法构造出的部分端元束(Cuprite)Fig.11 Partial endmember bundles constructed by SEVU algorithm(Cuprite)
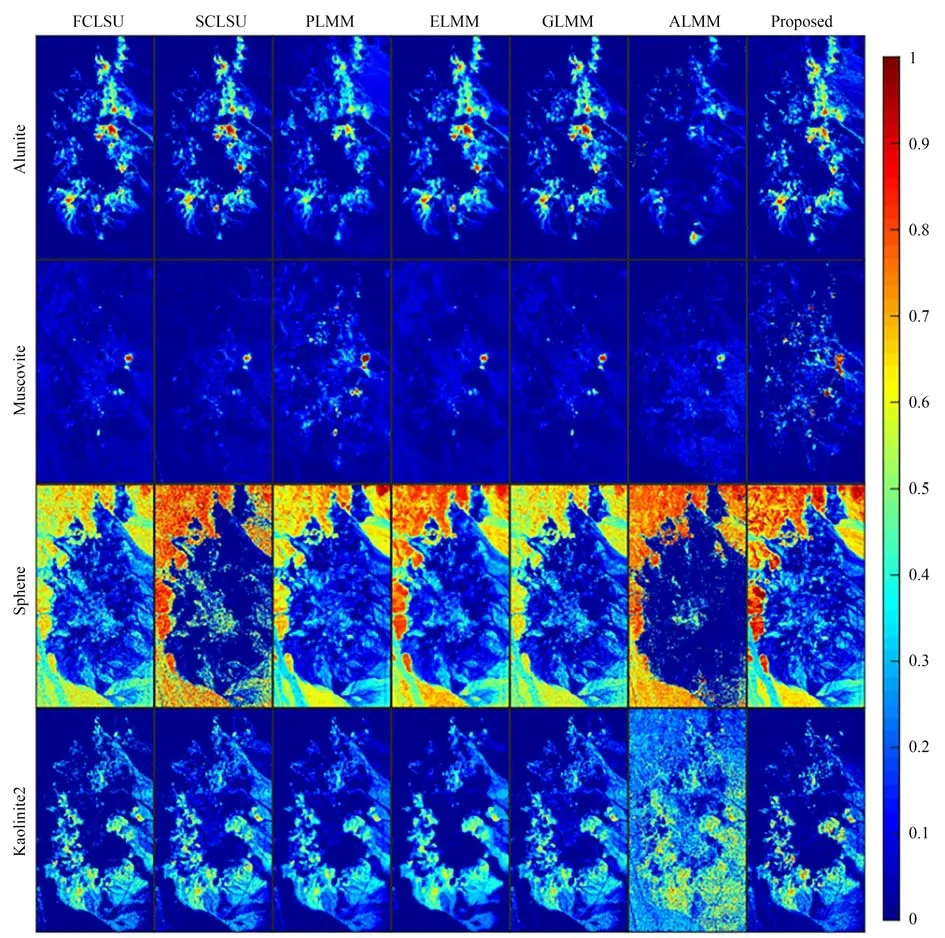
图12 各个算法估计的部分丰度(Cuprite)Fig.12 Partial abundance estimated by each algorithm(Cuprite)
4.2.6 算法收敛性分析
大多数基于LMM 的变体算法的求解都是非凸的,因此需要大量的先验信息或施加较多的正则项来限制解空间的区域,使算法的优化尽可能收敛。目标函数值随算法迭代次数的曲线可以从主观上判断算法的收敛情况,通过图13 可以看出对于不同噪声场景下的合成数据集和真实数据集,SEVU 算法的收敛性较好。
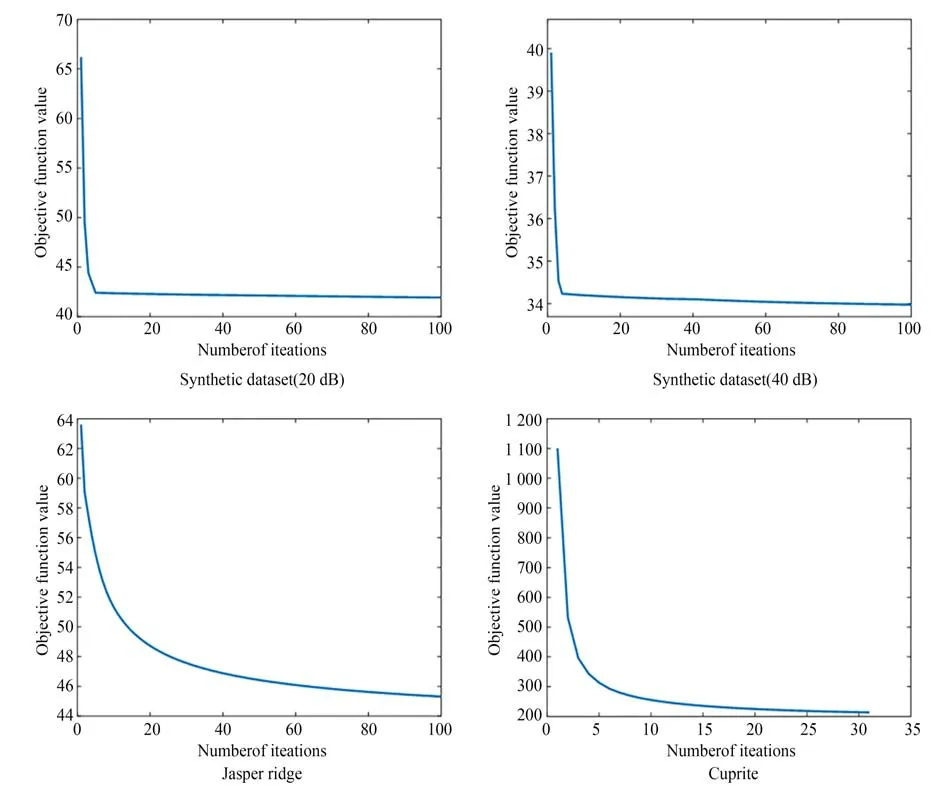
图13 目标函数随算法迭代次数的曲线Fig.13 Profiles of the objective function with the number of iterations of the algorithm
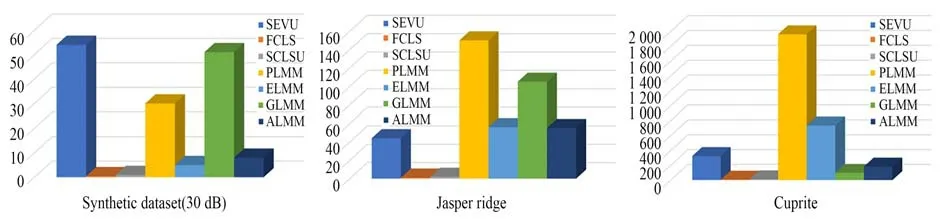
图14 算法运行时间对比(s)Fig.14 Comparison of algorithm run times(s)
4.2.7 算法运行时间
尽管SEVU 算法同时使用尺度因子和扰动构建端元的变异性,由于使用超像素分割算法作为空间上的预处理来划分局部同质区,而求解超像素内各像元的丰度向量使用丰度全约束(ASC,ANC)的FCLS 算法效率较高,这极大降低SEVU 算法运行的复杂度。通过图 14 可以看出,SEVU 算法的运行时间在图像较为复杂的时候有较大优势,而真实的场景中图像往往比较庞大且复杂,说明SEVU 算法在真实场景中应用的可行性。
5 结论
本文改进了PLMM,引入尺度因子的同时并利用超像素分割算法划分局部同质区,最后设计出一个基于局部同质区内共享端元变异性的SEVU 算法。在合成数据集和真实数据集上进行一系列实验,相较于PLMM,SEVU 算法在各个数据集上的端元误差降低了1.78%~3.23%,丰度误差降低了0.26%~2.42%,并且在大多数场景下SEVU 算法的解混效果优于对比算法,实验结果验证SEVU 算法的有效性和可行性。
