基于高斯混合分布及EM 算法的抗干扰定位方法
2024-04-07陈洪转由立华
初 飞,陈洪转,由立华,杨 立
(1.南京航空航天大学经济与管理学院,江苏 南京 210016;2.北京微电子技术研究所,北京 100076)
0 引言
随着全球卫星导航系统的发展和技术进步,越来越多的应用对于定位精度及可靠性有较高要求。在电子对抗环境中,导航接收机会收到多种干扰信号,如多径干扰、欺骗干扰(包括转发式和欺骗式干扰)等,尤其是欺骗干扰,真实信号和干扰信号的同时存在会导致接收机的定位结果出现较大偏移,甚至不在同一区域内,误导接收机的定位。与能可靠定位的真实信号相比,转发式欺骗干扰可被视为其在真实伪距观测值的基础上附加了额外的等效偏移,即伪距观测值存在异常偏移,生成式欺骗干扰可被视为接收到当前星座图不存在的伪距观测量,或当前星座图下虚假的星历信息。对于接收机而言,在众多真实信号与欺骗式干扰信号同时存在的复杂电子对抗环境中,将真实信号进行识别,存在较大的困难。现有的接收机大多使用RAIM 算法[1-8]及其增强算法(ARAIM)对伪距异常进行识别,但该方法主要针对民航飞机[9-11]、城市峡谷等应用场景,发生伪距异常的观测值个数一般小于两三个,远远少于真实信号的数量。在欺骗式干扰环境下,干扰信号的数量可能接近甚至超过真实信号的数量,此时现有的RAIM 方法已不再适用。
传统的RAIM 算法[1-2]大多基于最小二乘,构造卡方或T 统计量等进行假设检验及故障星排除,或者使用基于观测子集的多解分离方法,如MHSS[4-7],前者一般一次只能剔除单颗故障星,后者需要计算的观测子集数目随故障个数增加而超指数增长[14-15],无法满足实时性要求。近年来有学者提出使用稳健的参数估计方法代替最小二乘估计[12-15],比如用Huber[13,16],Tukey’s bisquare[14-15]等损失函数替代最小二乘法中的残差平方和(等价于调整正态分布对数似然函数)。M 估计方法和MM 方法是目前最有效的RAIM 方法,可以获得更好的鲁棒性、更高的定位精度和较高的故障剔除率[14-15],但该方法依赖于可靠的定位初值。而可靠的定位初值需要识别出可靠的真实信号,往往需要构造多个观测组合子集,计算量复杂度较高,无法满足电子对抗环境下对实时性的较高要求。
针对现有RAIM 方法的不足[17-27],本文提出一种基于高斯混合分布及EM 算法的快速、稳健、高精度定位方法。首先,根据实时观测数据建立高斯混合分布模型,进行极大似然估计,确定实时参数,根据故障个数、偏差大小自动调整分布密度函数的形态及各观测量的权重,以实现高精度稳健定位,并实时报告其定位误差大小;其次,使用基于标准化绝对误差中位数的标准差稳健计算方法,判断干扰卫星,得到无干扰的伪距观测量标准差的可靠估计值,将干扰信号对标准差的影响大大降低,保证了故障识别的稳健性;最后,使用FAST-LTS 方法用于快速确定可靠的初值,降低了计算复杂度,使得子集方程组数目不随故障个数增加而增加。
1 模型及算法
1.1 对加权最小二乘进行标准化
首先对定位解算的线性模型进行化简,以便于后续的简化计算。假设最小二乘定位解算方程为Y͂=H͂β+ε͂,ε͂∼N(0,σ2Σ),其中,Y͂是伪距观测列向量,H͂矩阵的每一行为各个卫星的观测几何矢量和截距项等,β是位置、钟差等待求解的未知参数,Σ代表每个卫星伪距误差的协方差矩阵先验值,通常假设不同卫星的伪距测量值相互独立,Σ为正定对角矩阵,即Σ=diag{},为了有利于后续建模,这里对最小二乘定位解算方程进行线性变换:
使得Σ-1/2ε͂∼N(0,σ2I),其中I是单位对角阵。
对于Σ-1/2有如下变换:
这里的线性变换为矩阵行变换,即对每颗卫星的观测量和几何矢量等进行标准化,把加权最小二乘计算转换为普通的最小二乘计算,可使矩阵运算的次数进一步降低,于是得到:
式中,i=1,…,n,n为卫星总数。yi为标准化后的伪距残余观测量,即标准化后的第i颗卫星的伪距观测量与导航接收机附近某点和该卫星的几何距离之差。hi为标准化后的第i颗卫星观测几何矢量及截距项,H为n×p维矩阵,p为未知参数个数,如当导航接收机含有钟差时,p=3+导航星座数,如单独使用GPS 或“北斗”导航系统时p=4,GPS、“北斗”导航系统联合定位时p=5,双差RTK 定位时p=3,此时钟差被消除。β为p维待求解参数向量,表示接收机的位置、钟差等。
1.2 建立误差分布模型
最小二乘方法假定1.1 节标准化后的伪距误差近似服从零均值方差未知的正态分布ε∼N(0,σ2I),在无干扰时能得到较好的定位精度。但有研究[28-29]发现,当多径、欺骗等干扰存在时,干扰信号与真实信号作为一个整体而言,其误差分布具有厚尾的特征,这是由于其中的干扰信号含有等效伪距偏差的缘故。
本文使用高斯混合分布对误差建模,在不同的参数下,既可描述干扰导致伪距存在偏差时的非零均值、厚尾、非正态的分布特征,也可以描述无干扰时真实信号的伪距观测量的零均值正态分布等。其好处在于,通过调整合适的参数,可使实际分布与模型假设更为吻合,以求解更可靠更高精度的定位结果。
高斯混合分布[30]的概率密度函数可分解为K个正态分布密度的加权和,权重为K个成分的先验概率,其中的每个正态分布为一个成分。形式如下:
fm(yi)表示高斯混合分布的概率密度,fk(yi)表示其中第k个组成成分的概率密度函数。
K为高斯混合分布中成分的数目,考虑到存在干扰信号时,可能存在等效伪距误差的方差放大或均值漂移等特征,本文令K=3 且μ1=0,高斯混合分布中的3 种成分分别描述无干扰、干扰导致方差增加、均值漂移这3 种情况下的伪距误差分布。待求解的参数向量为(βT,μ2,μ3,,γ1,γ2)T,其中后7 个参数为高斯混合分布的参数。需要说明的是,本文假设μ1=0,即高斯混合分布中第一个成分为零均值且误差未知的高斯分布f1(yi),用于描述真实信号的误差分布。其中γ3=1-γ1-γ2为冗余参数。其他2 个高斯成分f2(yi),f3(yi)均为均值非零且方差未知的正态分布,用于描述干扰信号的伪距误差分布。
在不同参数下的高斯混合分布密度函数示意图如图1 所示。黑色曲线表示某个零均值正态分布的密度函数,红色曲线表示某种厚尾分布,与黑色曲线代表的正态密度函数相比,其两端尾部的概率密度有明显提升。蓝色曲线和绿色曲线分别表示含有多个峰值的非对称的密度函数,可以用来描述多种干扰导致的伪距偏差等情形。
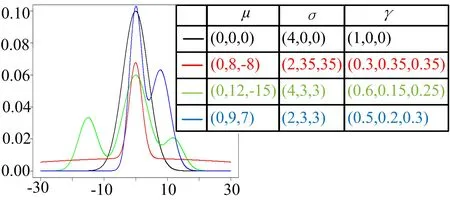
图1 不同参数下的高斯混合分布密度函数
从图1 中可以看出,本文使用高斯混合分布对误差建模,在不同参数下,可以用来描述误差的不同特性。在每一次定位时,都使用1.3 中的方法,利用实时观测数据进行参数极大似然估计,得到实时的误差分布情况,根据实时的干扰个数、偏差大小等自适应地调整分布参数,并进行稳健的定位解算。
该高斯混合分布的期望和方差可计算如下,该方差将用于1.5 中实时定位误差的计算:
1.3 使用EM 算法进行参数求解
直接对式(7)使用极大似然估计方法,可利用各参数的导数,使用梯度下降或牛顿法进行迭代求解其最大值,但该方法收敛较慢。本节使用EM 算法[30]对β等参数进行估计。EM 算法常被用于高斯混合分布下的参数估计,通过添加隐变量,使复杂的概率密度转化为简单形式的复合,将复杂的极大似然求解转化为一系列简单问题的求解,并且其具有良好的收敛特性,EM 算法每一步均使得期望极大似然值更大,可快速收敛到稳定值,具体求解过程如下:
为每一颗卫星增加隐变量zi,zi的无信息先验概率为P(zi=k)=γk,k=1,…,K。 令K=3,zi=1,2,3 分别表示第i颗卫星的观测值处于无干扰、存在某种干扰导致均值漂移或方差增大、或另一种干扰这3 种可能的状态。zi为未知的随机变量,可以基于观测数据yi等计算其后验概率(见1.4 节中γik)。
特殊情况下,当第i个观测卫星和第j个卫星为同时接收到的同一个卫星的真实信号或干扰信号时,即∃j,j=1,…,n,使得PRN(i)=PRN(j),此时添加约束P(zi=1)=P(zj≠1)。添加隐变量zi后,伪距残差yi关于zi的后验概率密度为:
添加隐变量zi后,后验密度转化为形式简单的正态分布。
式中,θ=(βT,μT,(σ2)T,γT)T为全部待估参数。μ=(μ1,…,μK)T,σ2= ()T,γ= (γ1,…,γK)T,μ1=0。
(yi,zi)为完全数据,其中yi为已知的观测数据,zi为缺失数据,但可以计算其基于观测数据的后验分布,对缺失数据zi通过求期望(积分)的方式进行消除,只保留观测数据。
添加隐变量zi后的完全数据概率密度为:
则完全数据对数似然为:
式中,Z=(z1,…,zn)。
参数求解分为E步和M步2 步:
1)E步:计算期望对数似然Q(θ|θ(t),Y)。
对关于Z的后验分布求期望,即
如果对于∀j,j=1,…,n,都有PRN(i)≠PRN(j),则:
如果∃j,j=1,…,n,使得PRN(i)=PRN(j),则:
t为迭代次数,初值θ(0)的选取见1.4 节。
2)M步:极大化Q(θ|θ(t),Y),得到θ(t+1)。
首先,关于γk极大化Q(θ|θ(t),Y),得到。
然后,关于(β,μ,σ2)极大化Q(θ|θ(t),Y):
分2 步计算,具体如下:
① 第1 步:固定(σ2)(t),求使Q(θ|θ(t),Y)达到极大化的(β,μ)(t+1)。
等价于求下列拓展线性方程的加权最小二乘估计:
可以看出,每一步更新β(t+1)的时候,与稳健回归方法如M 估计法[13]、MM 估计法[14-15]等类似,亦可转化为加权最小二乘形式,但不同之处在于,本文的权重是由每一个观测值在高斯混合分布中3 种不同成份的后验概率及各个高斯成分的μk,共同决定,每一次迭代自动更新。
② 第2 步:在(β,μ)=(β(t+1),μ(t+1))的条件下,求使Q(θ|θ(t),Y)达到极大化的(σ2)(t+1)。
如上所述完成一次迭代θ(t)→θ(t+1),重复进行直至‖Q(θ(t+1)|θ(t),Y)-Q(θ(t)|θ(t),Y) ‖或‖θ(t+1)-θ(t)‖或充分小时停止,得到全部未知参数的最终估计值=θ(t+1),以及故障状态的后验概率。
1.4 迭代初值的选取
本文选用FAST-LTS 方法的结果作为β的初值,该方法对现有的LTS 方法进行了一些改进,大大减少了运算次数。由于MM 法在使用LTS 法作为初值时[14-15],需要计算并比较所有可能的观测量子集,且需要对子集大小进行人为假设,因此,随着故障个数增加,MM 估计方法的运算复杂度增长较快。有学者提出基于特征斜率的快速选星方法[14-15],减少了LTS方法的方程组合数,但计算量仍较大,从现有的实证结果来看,目前能够支持的最大故障个数不超过3个[14-15]。故本文使用FAST-LTS[16]算法用于对LTS方法进行快速计算,其核心思想在于根据未知参数的个数确定最佳抽样次数,并减少方程组中的观测量数目,使含有无干扰组合的可能性大于99%,初次迭代后仅保留少数最优组合进行最终迭代,可在保证估计效率的同时,减少时间消耗[16]。
高斯混合分布的各参数初值可根据经验尽量使分布密度扁平、厚尾、对称。μ可根据长期观测的误差中位数来确定,σ可取大于伪距误差的值作为保守估计。
1.5 实时定位误差
最小二乘方法在定位之后,还计算了代表实时定位误差大小的协方差矩阵。本文所提方法的定位结果̂=β(t+1)的协方差矩阵可以利用式(23)计算如下:
由于YE中yi重复出现了3 次,故cov(YE)非对角元不全为0。根据式(9)和式(15)-式(17),可以计算Y的后验协方差矩阵ΣY,ΣY为对角矩阵,仿照式(9)计算,将γk替换为式(15)-式(17)中后验概率γik即可。
2 实验结果
2.1 实验设计
为了比较不同方法的效果,本文收集了GPS L1频点和“北斗”B1频点24小时实测数据进行模拟。固定天线位于办公楼顶层(经度39.8°、维度116.4°,高程85 m),采样率为1 Hz,采集时间为2021 年12 月23 日,GPS 和北斗的可见卫星为9~12 颗,卫星总数约20~22 颗,仰角阈值为5°,载噪比阈值为25,使用伪距定位。
为了最大化卫星几何分布的多样性,防止样本选择带来的偏差,本文从24 h 观测数据中选择可见卫星数超过20 颗的数据,使用均匀分布从中随机抽取3 000 s 观测数据,并以均匀概率随机剔除多于卫星,保证每秒样本中可见卫星数量为20 颗,作为2.2 和2.3节的实验数据。选择持续锁定20 颗以上卫星的3 000 s观测数据,剔除20 颗以上的多余卫星,作为2.4 节缓变偏差的实验数据,进行仿真。随机选取0~10 颗卫星作为干扰卫星,采用3 种模式(随机、固定和缓变)人为加入伪距偏差,比较4 种定位方法的定位精度。
本文计算了各种实验条件下三维 ENU 方向的均方根误差(RMSE),值越高表示定位精度越差。限于篇幅,本文仅以U 方向即高度方向为例,单位为m,以长期RTK 测量值作为参考真值。
选择了4 种解决方法进行比较:
方法1(记为LS):最小二乘估计,未进行故障识别和排除。
方法2(记为M):M 估计方法[13](Huber loss)。
方法3(记为MM):MM 估计法[14-15]。
方法4(记为GM3):本文提出的高斯混合模型及EM 算法。
对人为加入的等效伪距偏差,采用下面3 种模式设计:
模式1:随机偏差,以均匀分布随机为伪距观测量注入5~30 m 的偏差。干扰卫星数量依次从0 增加到10,故障为0 用于比较各方法在无干扰时的定位精度。
模式2:固定偏差,分别为伪距观测量加入15 m、20 m、30 m 的固定偏差。干扰卫星数量同模式1。
模式3:缓变偏差,分别以0.01 m/s、0.03 m/s 和0.02 m/s 的速度随机选择4、6、8 颗干扰卫星并为其伪距观测量加入偏差。
2.2 定位误差分析(随机偏差)
使用2.1 节中的模式1,在干扰信号的数量为0~10 的条件下随机选择干扰卫星进行模拟,得到4 种方法的高度误差如图2 所示,横坐标代表干扰信号的数量,即存在干扰的伪距观测值数量,纵坐标代表高度误差,4 种颜色代表不同方法。可以看出,当干扰数小于等于4 时,GM3 法的定位误差略高于MM 法,但差距小于0.4 m,仍低于M 法和LS 法。 当干扰数大于4时,GM3 方法的定位误差明显低于其他3 种方法,例如,当干扰数为7 时,定位误差与其他3 种方法相比减少了2 m 以上。
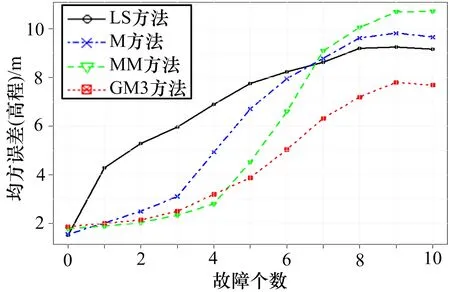
图2 4 种方法的高度误差比较
2.3 定位误差分析(固定偏差)
此处使用模式2,分别增加15 m、20 m 和30 m 的固定偏差。结果如图3—5 所示。总体而言,GM3 方法的定位误差最小。只有当干扰数小于等于3 时,其均方误差略低于其他方法,但差值小于0.2 m。当干扰数大于4 时,GM3 方法的均方误差显著低于其他方法。当20 颗卫星中有一半包含30 m 的偏差时,GM3方法、M 估计方法、MM 估计方法的高度误差分别为7.5 m、14.4 m、 和15.8 m,GM3 方法的定位误差仅是MM 估计方法的47%。
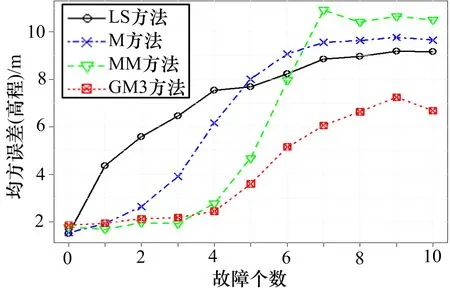
图4 4 种方法的高度误差比较(20 m 偏差)
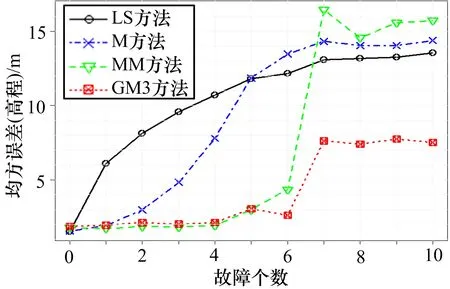
图5 4 种方法的高度误差比较(30 m 偏差)
2.4 定位误差分析(缓变偏差)
此处分别在干扰数为4、6 和8 时使用模式3 进行实验,结果如图6—8 所示,图中的4 种颜色代表4 种方法。
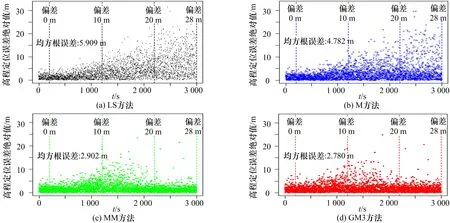
图6 4 种方法在偏差缓变时的高度误差比较(偏差速率0.01 m/s,干扰数目为4)
在图6 中,以0.01 m/s 的速度注入偏差,随机选择4 颗干扰卫星并保持不变,从第200 s 开始逐渐注入伪距偏差。纵轴为4 种方法高度误差的绝对值。为便于比较,纵轴使用相同的范围。图7 和图8 分别使用0.03 m/s 和0.02 m/s 的速度,随机选择6 颗和8 颗欺骗卫星,为其伪距观测量注入偏差,其他设置同图6,可以看出,随着偏差的逐渐增加,4 种方法的定位误差都有不同程度的增加,使用GM3 方法计算得到的定位误差增加速度较其他3 种方法更慢。表1 为4 种方法的定位精度比较,可以看出GM3 方法的平均定位误差最低,比如当8 颗卫星的伪距观测量存在偏差时,与其他3 种方法相比,GM3 方法的定位误差减少了6 m,说明GM3 方法在该恶劣环境下仍具有良好的定位表现。
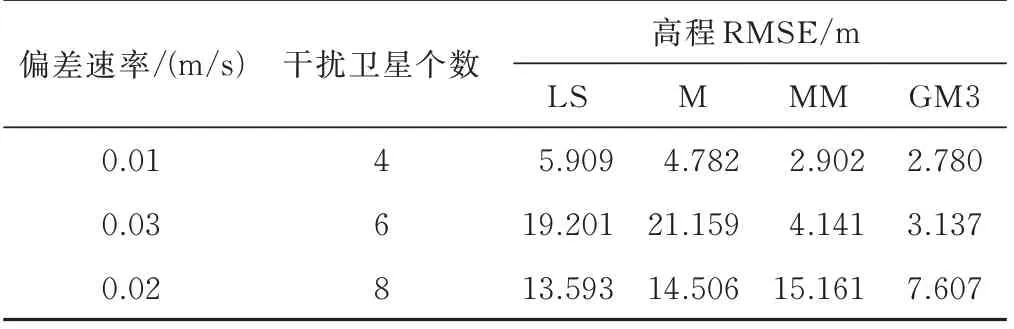
表1 定位精度比较
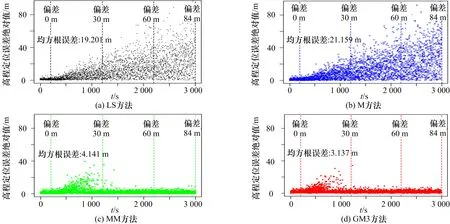
图7 4 种方法在偏差缓变时的高度误差比较(偏差速率0.03 m/s,干扰数目为6)
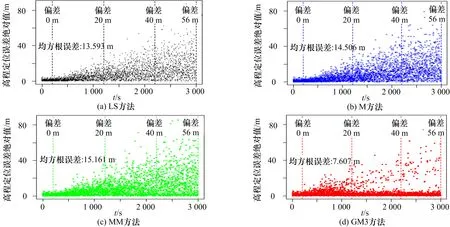
图8 4 种方法在故障缓变时的高度误差比较(偏差速率0.02 m/s,干扰数目为8)
2.5 实时定位误差分析
随机偏差模式下高程真实误差(VPE)和高程标准差stdv=(C33)1/2时序对比图及VPE/(2.58stdv)的直方图如图9 所示。2.58 为正态分布的99%分位点。从直方图可以看出,在大多数情况下,VPE/(2.58stdv)的绝对值小于1,即|VPE|<2.58stdv,实际误差VPE 小于标准差的2.58 倍,说明协方差矩阵的计算是有效的,可以反映实时误差的大小。
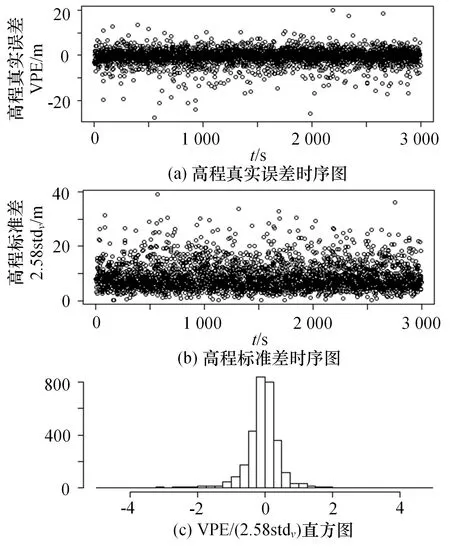
图9 高程真实误差、标准差的时序图及直方图(随机偏差,干扰数目为5)
2.6 时间复杂度
以2.2 节随机偏差场景为例,使用R 语言进行仿真程序的编写,得到4 种方法在不同干扰数下的平均运行时间,如表2 所示,考虑到不同硬件平台、不同编程语言的时间消耗不同,所以此处比较相对时间的变化。可以看出,本文所用GM3 方法的计算复杂度基本上与故障数量无关。 使用本文1.4 节提出的FAST-LTS 算法对LTS 方法进行加速后,LTS 方法计算迭代初值的时间与干扰数量无关,克服了其他方法如MM 方法[14-15]随着干扰数量的增加而方程组合个数呈超指数级快速增加的不足。同时,使用本文提出的EM 算法用于求解高斯混合分布的极大似然估计,加快了收敛速度。从表2 的实验结果可以看出,当干扰卫星个数为10 时,本文的GM3 方法的运行时间为23.17 ms,MM 方法的运行时间为113 443.87 ms,GM3方法将时间缩短为MM方法的1/5 000,说明本文提出的方法在干扰信号数量较多时,有良好的实时性。
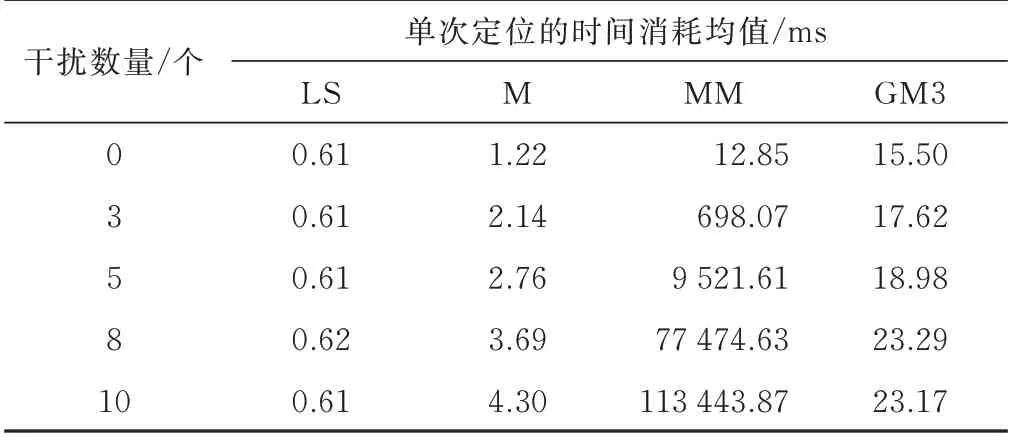
表2 不同干扰数量时的运行时间比较
3 结束语
在复杂电子对抗环境下,多个卫星的伪距观测量受到生成式或转发式欺骗干扰,导航接收机同时收到多个真实信号和干扰信号。将真实信号与诸多干扰信号进行分离,是接收机实现可靠、高精度定位的关键环节。目前,导航接收机多使用RAIM 及ARAIM算法进行干扰识别,但该类方法存在运算时间随故障数量增加而超指数增长、定位精度低且不可靠、仅支持3 个及以下干扰数量等缺点,无法满足电子对抗环境下对接收机当前位置、速度等状态的高可靠、高精度、实时性等要求。针对上述问题,本文提出一种高精度、高可靠、快速的抗干扰定位算法,使用高斯混合分布对观测误差建立极大似然估计模型,使用EM 算法进行快速解算,使用FAST-LTS 算法对迭代初值的计算进行加速。随机、固定和缓变3 种伪距偏差模式下的实验结果表明,当受到欺骗式干扰的卫星数量为10 个时,该方法相较于MM 等估计方法定位精度提升53%以上,计算时间缩短为其1/5 000。本文所提方法可用于多径、转发或生成式欺骗等多种干扰同时存在的电子对抗场景下的高精度、快速、可靠定位及干扰消除,具有广泛的应用价值。■
