基于KM 算法的转发式干扰辨识与抑制方法
2024-04-07杜思予陈望杰刘泳伶
季 权,王 松,杜思予,陈望杰,刘泳伶
(1.中国航天科工集团8511研究所, 江苏 南京 210007;2.中国人民解放军32086部队, 江苏 南京 210018)
0 引言
在现代复杂电磁环境中,干扰装备向综合化、分布化、灵巧化方向发展,新型干扰技术层出不穷。特别是随着数字射频存储(DRFM)技术的快速发展,基于DRFM 的干扰机能够对截获到的雷达信号进行分选、识别、存储,然后快速调制转发,产生大量相干干扰信号。此类干扰能够在雷达信号处理阶段获得匹配滤波增益,形成大量能量较大的假目标,严重影响雷达的目标检测与跟踪能力。
目前,国内外学者从重构对消和干扰辨识2 个方向出发,提出了许多行之有效的抗干扰方法。在重构对消方面,文献[1]基于自适应滤波估计干扰参数,重构出干扰信号,与原始回波对消;文献[2]从脉压数据中提取干扰参数重建干扰信号,进而实现干扰自适应对消。但是重构对消的思想对参数估计精度要求较高,若参数估计不准确,则干扰抑制效果不佳,也可能造成对消后目标信号的丢失。在干扰辨识方面,主要是利用目标和干扰在时域、频域、空域、时-频域、变换域等方面的特征差异进行信号识别、分类,从而抑制干扰信号。文献[3—4]设计了一种空-时相位编码信号,增强干扰与目标空-时分布差异,进而通过失配滤波器实现了干扰抑制;文献[5]利用快-慢时间联合域处理抑制干扰,但仅适用于非相干干扰;文献[6—8]分别对回波信号进行Hough 变换和分数阶傅里叶变换,根据变换域特征区分干扰和目标;文献[9—10]通过分析干扰和目标在脉压域的分布特征,检测目标所在距离单元并剔除干扰,但干扰功率较大时算法失效;转发式干扰的多普勒频率通常集中分布于有限个邻域内,文献[11]利用这一点区分干扰和目标;文献[12]设计频率、极化联合捷变波形,在接收端采用盲源分离算法抑制干扰。但此类方法无法适用单极化雷达,具有一定的局限性。
本文聚焦雷达对抗此类相干干扰的需求,首先对转发式干扰的产生机理和干扰特性进行了详细的分析,然后探讨了捷变频雷达波形抗此类干扰的能力,并结合频率捷变技术带来的主动对抗优势,提出了一种基于K 均值(KM)聚类思想的干扰抑制方法。
1 信号模型
1.1 转发式干扰
转发式干扰一般是指干扰机对所截获的雷达信号直接或进行幅度、相位、频率、时延等调制后发射出去的干扰。此类干扰信号和雷达信号具有一定相参性,能够获得雷达接收机的匹配滤波增益,从而在距离维产生与真实目标相似,但能量更强的若干个虚假目标,达到迷惑、欺骗雷达的目的,同时具有压制真实目标的干扰效果。
由于天线隔离度限制,实际应用中干扰设备多采用收发分时体制。干扰机对雷达发射信号进行采样预存储之后,经过延时直接转发或多次延时后叠加转发,可以形成单个或多个假目标干扰。通过调整采样时长和转发延时的时序关系,理论上能够在匹配滤波输出中实现任意密集度的假目标干扰效果。具体产生原理如图1 所示。

图1 转发式干扰产生机理
假设干扰机截获了第n个雷达发射脉冲st(t,n),延时K次,将产生的K个时延信号在时域进行叠加转发。因此,转发式干扰信号sj(t,n)可以表示为:
式中,Δτk,n表示干扰机产生的第k个干扰信号相对于第n个雷达发射脉冲的延时;Aj(k,n)表示第n个脉冲对应的第k个时延干扰信号幅值。干扰机工作带宽为[fj1,fj2]。
1.2 捷变频雷达信号
频率捷变是一种常用的干扰对抗手段。捷变频雷达是指雷达相邻发射脉冲间的载频随机或伪随机跳变,干扰机难以准确预测出下一个脉冲的频率,从而能够有效对抗大功率噪声压制干扰和大部分欺骗干扰。典型的捷变频雷达发射信号如图2 所示。图2中,f0表示初始载频,Δf表示跳频间隔。

图2 典型捷变频雷达发射信号
假设雷达在一个相参处理间隔(CPI)内共发射N个脉冲信号,则第n个脉冲信号st(t,n)对应的载频可以表示为:
式中,c(n)表示跳频编码,M表示跳频点数,且有M≥N。那么,捷变频雷达发射信号总带宽B=M⋅Δf,第n个脉冲信号st(t,n)表示为:
式中,t为快时间,u(t)为发射信号基带波形,采用线性调频(LFM)信号时,u(t)=rect(t/Tp)exp(jπκt2),κ=BP/TP表示线性调频斜率,Bp和Tp分别表示发射脉冲带宽和时宽,Tr表示脉冲重复周期。
以单个点目标为例,对于一个初始径向距离r0,速度v0,做匀速直线运动的刚体目标,捷变频雷达第n个脉冲的目标回波信号r(t,n)可以表示为:
式中,γ表示目标后向散射系数,τn=2(r0-v0(n-1)Tr)/c表示目标回波相对于发射脉冲的时延,c为光速。
2 抗干扰机理分析
干扰机利用截获的雷达发射信号产生与真实回波高度相关的转发式干扰,将会严重影响雷达的检测跟踪性能。转发式干扰效果如图3 所示,图3(a)和(b)分别显示了转发式干扰对LFM 信号和捷变频雷达信号的干扰效果。

图3 转发式干扰效果
可以看到,对于LFM 雷达而言,叠加的干扰信号均获得匹配滤波增益,使得真实目标淹没在密集的逼真假目标中,难以有效区分;对于捷变频雷达而言,由于干扰机收发分时,采样到第n个发射信号无法与后续第n+1,n+2,…,N-q个脉冲匹配,其中,q为不大于N的任意正整数。因此,捷变频雷达的回波信号中只有部分脉冲会受到干扰影响,这为后续的干扰辨识和干扰抑制处理提供了极大的便利。
由此,捷变频雷达接收机接收到的第n个脉冲的回波信号sr(t,n)可以表示为:
式中,n(t)表示随机高斯白噪声。进一步地,对接收到的回波进行混频和脉冲压缩处理,得到的输出为:
式中,复包络u(t)为LFM 信号,A表示真实目标回波经过脉冲压缩处理后的幅值,A′j(k,n)表示第k个假目标经过脉冲压缩处理后的幅值;n′(t)表示脉冲压缩处理之后的噪声信号。
综上所述,采用捷变频波形降低了干扰在频域的覆盖率,从发射端提升了雷达的低截获性能和抗干扰能力。
3 基于K-Means 聚类算法的干扰识别与抑制
KM 聚类算法是一种动态聚类算法,其主要思想是对N个待分选对象给出K(K≤N)个类划分,将特征集中在任意k类的待分选对象进行分类组织。KM 算法以误差平方和作为聚类准则,具有占有存储空间小、算法简单方便、聚类效率高等优势,广泛应用于雷达侦查领域,实现雷达辐射源信号分选与分类识别。雷达抗干扰技术也可以认为是一种信号分类识别的过程。因此,利用目标和干扰在脉压域的分布特征差异,本文基于KM算法实现干扰识别与抑制处理,具体过程如图4所示。
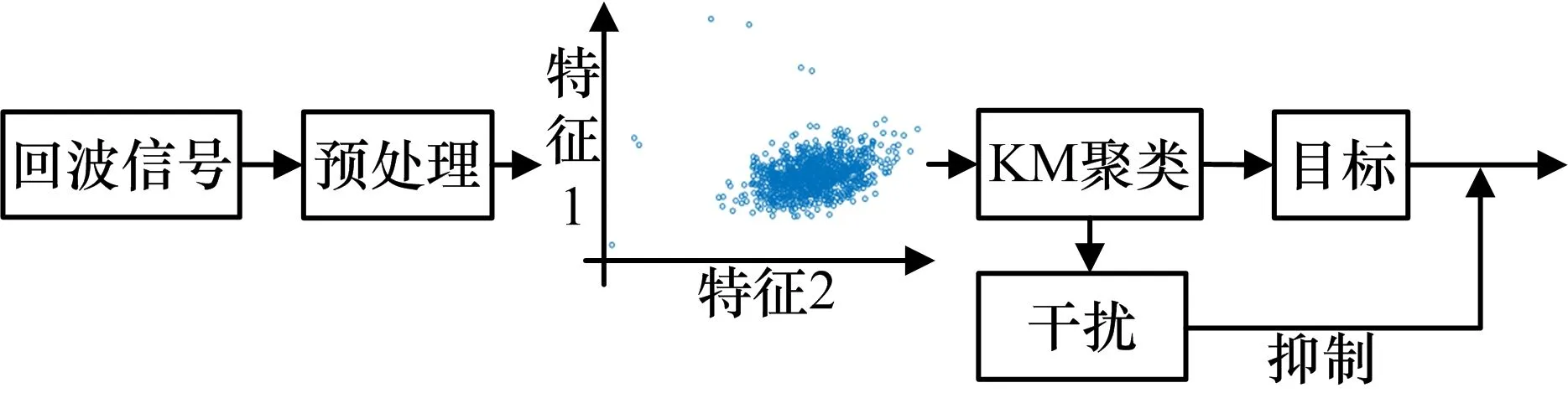
图4 基于KM 算法的干扰识别与抑制流程
3.1 数据预处理
式(5)和式(6)的推导结果表明,经过脉冲压缩处理之后,捷变频雷达的目标回波是一条连续的直线,而转发式干扰信号由于频率失配而呈现出一定程度的离散化,参照图3(b)。对于脉压数据矩阵中的每个元素,分别沿距离维和速度维计算离散度。具体定义为:
式中,n,l分别表示速度单元索引和距离单元索引,An,l表示第n个脉冲、第l个距离单元对应的幅值;ω表示当前单元的邻域长度。dr(l)表示第l个距离单元内脉压数据的距离维离散度,dv(l)表示第l个距离单元内脉压数据的速度维离散度。将dr(l),dv(l)构成数据集DL×L={dr(l),dv(l)}, 1 ≤l≤L。
3.2 干扰辨识与抑制
本文利用KM 聚类算法对回波数据进行识别、分类,进而实现干扰抑制。具体步骤如下:
步骤1:按照3.1 节对回波脉压数据进行预处理,得到待分类数据集D={d1,d2,…,dL},且dl=(dr(l),dv(l));
步骤2:初始化簇划分Ck=∅,k=1,2,…,K,从数据集D中随机选择K个样本作为初始聚类中心μk∈{μ1,μ2,…,μK};
步骤3:针对数据集中每个样本dl,计算其到K个聚类中心的距离Δk=,并将其划分到距离最小的聚类中心所对应的类λk中,此时Δλk=min {Δ1,Δ2,…,ΔK},并更新簇Cλk=Cλk∪{dl};
步骤4:针对每个类别对应的簇Ck中所有的样本点重新计算聚类中心μk=1/ |Ck|(即属于该类的所有样本的质心);
步骤5:重复步骤3—步骤4,直至聚类中心位置不再改变,聚类结果对应的损失函数最小,算法达到收敛。其中,损失函数定义为各个样本距离所属簇中心的误差平方和:
式中,dl表示第l个样本,Cl是dl所属的簇,μCl表示簇Cl对应的聚类中心,L为样本总数。
4 仿真实验
本节通过仿真实验验证所提抗干扰算法的有效性和干扰抑制性能。仿真参数如表1 所示。

表1 仿真参数设置
干扰抑制过程仿真实验结果如图5 所示。其中,图5(a)为捷变频雷达回波的脉冲压缩后结果,图5(b)为图5(a)的俯视图。可以看出,干扰机对截获到雷达发射脉冲信号进行多次转发,经过脉压处理之后,在距离向上形成功率较大的若干个假目标,覆盖真实目标。但是由于干扰带宽远小于雷达跳频带宽,因此只有部分脉冲受到干扰机影响。进一步使用KM 算法对散点图进行聚类,得到图5(c)所示的聚类结果。根据聚类结果,滤除干扰信号,所得结果如图5(d)所示。对比图5(a)可以看到,脉压距离单元内的假目标被抑制,只剩下目标信息,证明了所提算法抗转发式干扰的有效性。
5 结束语
本文联合捷变频雷达“主动”对抗优势,提出了基于KM 算法的抗转发式干扰方案。与现有算法相比,论文所提方法具有以下优势:不依赖于干扰和目标的多域特征差异,适用范围更广;算法逻辑和模型较简单,具有一定的工程实际意义。■
