基于落压式动力装置的挠性航天器姿态控制技术研究
2024-04-07胡诗桥刘国生戴曜泽
胡诗桥,陈 宁,刘国生,戴曜泽,时 中
(中国航天科工集团8511研究所,江苏 南京 210007)
0 引言
由于火箭发动机载重的严格限制,世界各国针对传统的刚性航天器进行改良以携带更多的有效载荷。研究了空间可展开结构[1]、太阳能帆板[2]、柔性机械臂[3]等柔性结构,其中空间可展开结构强度高、质量轻、体积小,在航天器中应用越来越广泛。典型的应用如可充气气球卫星[4]、空间站充气式垃圾舱[5]、巡飞弹柔性充气翼[6]、充气式导弹诱饵[7]。
当前研究的挠性航天器的姿态控制多以大型太阳能帆板、天线附件为主,文献[8]将滑模控制与模糊控制结合,用模糊控制改进了滑模面的切换增益,有效抑制了抖振。文献[9]考虑了刚性主体和挠性附件的弯曲运动,设计了滑模控制器,能够有效的对姿态动力学方程进行精确跟踪,并且能够抑制结构振动,实现了工程应用。上述文献对充气可展开结构的挠性航天器有一定的参考价值,但在工程应用中较为复杂。文献[10]在传统的Bang-Bang 控制和Bang-coast-Bang控制对模型误差要求极高的背景下,通过一个新的目标函数,一项与总机动时间成正比,一项与积分成正比,设计了一种平滑且次时间最优的挠性航天器姿态机动算法来跟踪优化参考姿态轨迹。文献[11]研究了柔性充气空间飞行器的姿态控制系统,采用了线性自抗扰控制、PWPF 以及滤波处理等方法,有效抑制充气囊体的挠性振动,减少了燃料的消耗,但是其采用恒压式结构相比落压式结构在增加航天器质量的同时,还增加了工质的消耗。
本文以短时、大干扰力矩的充气可展开结构航天器为研究对象,基于线性自抗扰技术,研究以落压式微推力器为执行机构的挠性航天器大角度机动姿态控制算法,通过发动机气体动力学公式拟合动力装置实时压力变化曲线,得到落压式推力器输出推力的实时值,实现了挠性航天器高姿态控制精度的大角度机动,减少了工质的消耗,增加了姿态保持时间。
1 航天器姿态控制模型
本文参考挠性航天器的姿态动力学以及运动学方程在321 转序下对航天器建模[12]。
1) 运动学方程
以四元数的形式描述航天器姿态:
式中,q=[q0,q1,q2,q3]T,qs=q0,qv=[q1,q2,q3]T,ω=[ωx,ωy,ωz]T,为航天器的体轴角速度,I3为3×3的单位矩阵,为叉乘矩阵,其定义为:
2) 动力学方程
式中,J是航天器的转动张量矩阵,其定义为:
式中,Jx、Jy、Jz为航天器的主轴转动惯量,Jxy、Jxz、Jyx、Jyz、Jzx、Jzy为惯量积,ω=[ωx,ωy,ωz]T为航天器的体轴角速度,η为航天器的挠性模态η=[η1,η2,…,ηi],i为选取的挠性模态阶数,Fs为挠性航天器的刚柔耦合矩阵,其矩阵维度根据挠性模态的阶数而确定,u是航天器的控制力矩u=[ux,uy,uz]T,d是航天器受到的外部总干扰d=[dx,dy,dz]T。
式中,ξi为挠性振动的阻尼比,Ωni为挠性振动模态阻尼矩阵,N为挠性模态的阶数。
2 姿态控制设计
姿态控制基于误差四元数和误差角速度控制,在PD 控制算法的基础上,采用线性自抗扰算法,利用推力器喷管的非线性bang-bang控制将自抗扰控制的线性姿态控制量转为为非线性0-1 控制信号,设计姿控喷管开关门限,控制喷管电磁阀的开关,实现航天器的姿态控制。基于自抗扰控制的姿态控制方案如图1 所示。

图1 基于自抗扰控制的姿态控制方案
图1 中qd是期望姿态角转换得到的期望姿态四元数,q为实时的姿态四元数,qe为误差四元数,其定义为:
定义qe=[qe0,qev]T,qev=[qe1,qe2,qe3];kp、kd为PD 控制的参数,w为MEMS 陀螺仪测量角速度,wf为滤波处理角速度,uo是PD 控制输出的控制力矩,经过开启门限判断,控制推力器电磁阀的开关,输出控制力矩u,d是航天器所受的干扰力矩。PD 控制具体的控制方程:
式中,uc=[ux,uy,uz]T,kp=diag[kpx,kpy,kpz],kd=diag[kdx,kdy,kdz],ωe是误差角速度,在期望角速度ωd为0 时,ωe=ω。
线性自抗扰控制采用线性状态观测器,将航天器受到的干扰进行估计并实时补偿PD 控制的输出,从而实现航天器姿态的高精度控制。
利用航天器的动力学方程,角速度ω为系统的输出,得到:
由于喷管开启时,系统的转动惯量在不断变化,将控制力矩以外的量视为总干扰,得到:
式中,f(t)=J-1(d-ω×Jω-FTs η̈),K=J-1,令x1=ω,x2=f(t),y为系统的输出,系统的状态方程为:
由于f(t)与K已知,对一阶系统设计线性二阶状态观测器,令z1为x1的估计,z2为x2的估计,e1为x1的误差,e2为x2的误差,β1和β2为待定参数。
此时系统的误差方程为:
利用欧拉法求解微分方程ż(t)=(z(t+h)-z(t))/h,此时状态观测器的解为:
式中,h为仿真步长,z1(t+h)为下一时刻x1的估计,z2(t+h)为下一时刻x2的估计,使用带宽法进行参数整定,系统矩阵的特征方程为s2+β1s+β2,通过β1和β2的取值使得观测器稳定,将特征方程的根都设计在ω0处,特征方程变为(s+ω0)2,系统稳定。
姿控喷管采用0-1 非线性控制,其控制原理如图2 所示。

图2 非线性开关特性曲线
图2 中K表示姿控喷管的开关,1 为正开,-1 为负开,0 为关闭,Eom和m为开关参数。
开关函数如下所示:
本文选用冷气推进系统为航天器姿态控制的动力装置,将气体存储在高压气瓶内,气体通过微推力器喷管喷出而产生推力。动力系统采用落压工作模式,不配备恒压阀,降低了气瓶组件的质量,在工作过程中喷管处压强与气瓶内压强的变化相同,由于压强不断降低,导致微推力器推力不断下降,需要对气瓶内的压强进行实时拟合,从而得到喷管处推力的实时变化曲线,提高姿态控制的精度。气瓶内的实时压强公式、质量流率公式与推力公式如下[10]:
式中,p表示气瓶内的实时压强,单位是pa;V表示气瓶的容积,单位是m3;m0表示气瓶内初始的气体质量,单位是g;Δm表示工作过程中气瓶内消耗的气体质量,单位是g;M表示气体的摩尔质量,单位是g/mol;R为摩尔气体常数,单位是m3·pa·mol-1;T是温度,单位是K;ṁ是气瓶内的质量流率,单位是kg/s;At是喷管的喉部面积m2;γ是气体比热比,无量纲;R0是气体常量,不同气体取值不同,单位是J·kg-1·K;Cf是推力系数,无量纲。
3 仿真验证
3.1 航天器姿态控制任务需求
航天器姿态控制任务输入输出如表1 所示。航天器的姿态控制要求如表2 所示。

表1 姿态控制任务输入输出

表2 姿态控制要求
3.2 落压式推力曲线拟合
仿真参数设置如下:气体初始质量m0=30 g,气瓶体积V=0.62×10-3m3,氮气摩尔质量为28 g/mol,R取值为8.31 m3·pa·mol-1,温度T=300 K,喷管喉部面积At=8×10-8m2,氮气比热比γ=1.4,氮气的气体常数R0=296.8 J·kg-1·K,推力系数Cf= 1.25。将式(17)求解并代入式(16),并在仿真软件中仿真,由于落压式在实际应用中电磁阀的磁滞特性等问题,会导致落压式曲线拟合与实际情况有误差,因此在落压式曲线拟合过程中加入噪声模块,噪声采用simulink中的band-limited-white noise 模块,该模块可以生成正态分布的随机数。气瓶压强与推力工作时间变化曲线如图3 所示。

图3 气瓶压强与推力工作时间变化曲线
由图3 可得在本文的初始参数条件下,气瓶的初始压强为4.3 MPa,落压式推力器初始推力为0.43 N,工作时长约为100 s。
3.3 姿控仿真
对以恒压式微推力器以及落压式微推力器为执行机构的挠性航天器进行姿控仿真,恒压式三轴的推力均为0.2 N,落压式的初始推力为0.43 N,两者均以氮气为工质,气瓶初始气量均为30 g,姿控任务需求如表1 所示。航天器结构参数如下:
系统的转动惯量矩阵:
振动频率矩阵:
振动阻尼矩阵:
耦合系数矩阵:
PD 控制参数:
状态观测器控制参数β1=0.4,β2=0.04;开关控制参数Eom=1°,m=0.9。
三轴干扰力矩:
仿真时长为3 200 s。
图4—6 所示为恒压式推力与落压式推力三轴姿态角仿真曲线对比,图7-8 所示为喷管开启时间曲线对比和气瓶剩余气量曲线对比。
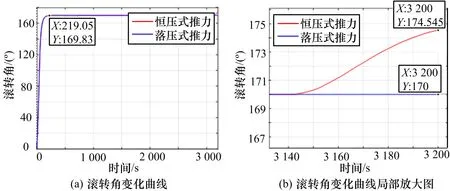
图4 滚转角仿真曲线对比

图5 俯仰角仿真曲线对比

图6 偏航角仿真曲线对比

图7 喷管开启时间曲线对比
从姿态角的变化曲线可得落压式推力器与恒压式推力器调姿到位的时间相同,均满足姿控需求,并且落压式推力器在俯仰角方向的超调量较小,系统稳定性更高。姿态保持阶段,两者姿态角误差均在其0.2°以内,满足姿控精度的需求,但是在姿态保持阶段,恒压式在3 140 s,开始发散,不能满足姿态保持时间需求。
由图7 可知,恒压式微推力器下由于在3 140 s 气量耗尽,喷管保持常开状态导致开启时间迅速增加,落压式微推力器下喷管开启总时长为79.64 s。由图8可知,落压式微推力器在3 140 s 左右剩余气量约为2.7 g,工质消耗相比于恒压式微推力器减少约10%,仿真结束时,落压式剩余气量约2.3 g,经过后续仿真,剩余气量可以增加约11%的姿态保持时间。

图8 气瓶剩余气量曲线对比
4 结束语
本文根据挠性航天器动力学与运动学模型,建立充气可展开结构航天器的数学模型,基于自抗扰控制+非线性bang-bang 控制、气体的状态方程、火箭发动机流量方程和推力公式等方法建立了落压式微推力器的航天器姿态控制仿真模型,并通过仿真验证,所得结果与恒压式推力对比,得到以下结论:
1) 通过火箭发动机气体动力学公式对动力装置中压力进行实时拟合,根据推力公式,得到了落压式推力器推力随工作时间的变化曲线,并应用于姿态控制仿真中的推力器模块,提高了姿态控制的精度;
2) 将得到的推力变化曲线应用于挠性航天器姿态控制,并将仿真结果与恒压式微推力器仿真对比,落压式微推力器在姿态控制精度、响应时间与恒压式相同,在俯仰通道姿态控制曲线的超调量较小,提高了系统的稳定性。落压式减少了约10% 工质的消耗,增加了11%姿态保持的时间,同时与恒压式微推力器相比,落压式微推力器不配备恒压阀、压力传感器,进一步实现了航天器的小型化、轻量化。■
