飞机上刹车杆仿竹轻量化结构及响应面法优化

张霄昕，王琦，何国毅，杨辉

（南昌航空大学 飞行器工程学院，南昌 330063）

飞机设计领域有一句名言：“为降低每一克重量而奋斗”。数据表明，飞机结构重量每减轻1%，飞机性能就能提高3% ～ 5%[1]，因此重量是衡量飞机设计先进性的重要指标之一。

起落架是飞机重要的受力部件，而且大型飞机的起落架重量较大。对起落架进行重量优化具有实际意义。

针对起落架优化和轻量化的研究，刘文斌等[2]对某型无人机起落架进行优化，采用拓扑优化的方法进行迭代，大大降低了结构重量和应力水平；张明等[3]根据起落架不同设计阶段需求，先后运用拓扑优化、尺寸优化和形状优化技术进行优化设计，与传统优化方法相比，切实提高了起落架的设计效率和性能，结构重量得到大幅降低；李静和张显余[4]对某型飞机主起落架车架前轮叉进行了静力学分析,得到前轮叉薄弱部位,利用拓扑优化和多参数优化方法对结构进行了优化，降低了其结构质量，并改善了受力情况；对于起落架强度分析问题，何雪浤等[5]对飞机起落架的四框架进行了有限元强度分析，表明采用线形载荷分配形式对所分析的四框架型材进行有限元应力分析,能够得到接近型材实际工作时的应力分布情况；Tugay 和Türkmen[6]设计了一款小型无人机起落架，根据有限元分析结果，确定了最佳的形状、材料和层合板构型，实验结果表明优化之后的结构性能有明显提高。然而，国内外对于起落架结构的研究大多是进行性能上的试验，其设计也多是停留在设计师的经验化设计以及通过仿真分析的试错法，最终所得到的设计结果难以保证达到最优化设计，对于结构设计的详细优化阶段、局部设计阶段的先验型知识研究较少。

本文以轻质高强的竹子结构为模板，对原十字上刹车杆分析中发现的支耳外侧与肋板连接处容易发生应力集中的现象进行优化，采用响应面优化设计方法对仿生结构进行详细设计，避免应力集中现象并降低结构重量。

1 十字上刹车杆的建模与静力学分析

1.1 建立有限元模型

图1 是我国运八飞机的主起落架结构。根据文献[7]结果，建立起落架的上刹车杆构件三维模型，如图2 所示。

图1 运八的主起落架结构及十字上刹车杆位置Fig.1 The structure of the main landing gear and the position of the cross-shaped brake rod of Y-8 aircraft

图2 十字上刹车杆Fig.2 The cross-shaped brake rod

上刹车杆的主要工况是受拉[8]，所受载荷为350 kN；约束条件为一端支耳内孔在3 个坐标方向固定，另一端支耳内孔沿轴向施加拉力并约束其余两个方向，只能沿轴向产生位移。采用30CrMnSiNi2A高强度合金钢，其弹性模量为211 GPa、泊松比为0.3[7]。

1.2 静力学分析结果

十字上刹车杆的静力学分析结果如图3 所示。由分析结果可以看出，在其主要工况下会在上刹车杆接耳外侧与肋板连接处出现应力集中现象，也是最大应力值的位置。其最大等效应力值为1 069 MPa，接近许用应力极限，安全系数较小，容易产生破坏。

图3 十字拉杆的静力分析Fig.3 Static analysis of the cross-shaped brake rod

2 上刹车杆的圆形设计和静力学分析

根据上刹车杆的相关尺寸，十字杆两端的支耳外直径与中间十字肋板的截面较小跨度处都是60 mm（图2），所以将圆柱实体杆的柱体外直径设计为60 mm 并与支耳融为一体，如图4 所示。其中刹车杆两端的圆柱支耳柱体高度和内外径尺寸与十字上刹车杆尺寸相同，总长度完全相同，且支耳与柱体相接处有充足的凹槽长度不会影响其他零件的正常转动。

图4 圆柱状上刹车杆Fig.4 Cylindrical brake rod

通过圆形实体刹车杆的静力学分析结果，得知圆柱实体刹车杆能大大降低危险处的最大应力值和总体变形量。但是圆形实体刹车杆的质量为10.379 kg，十字刹车杆的质量为6.940 9 kg，所以还可以进一步对圆形实体拉杆进行中空的仿竹微观结构的优化设计。

3 仿生结构的设计

3.1 仿竹微观结构设计

竹壁是竹子优良力学性能的物质基础，其中有多种不同形态结构的细胞。从力学角度来考虑，这些细胞可分为两类：1）基本组织细胞，它们是薄壁结构起着传递载荷的作用；2）以维管束为主的厚壁细胞，它们被基本组织细胞包围着，起着承载的作用。同时，在维管束内存在大量的细胞壁更厚的管形细胞，它们大大加强了竹子的强度等力学性能，而这种细胞在外皮层的密度最高然后逐渐变低到靠近内皮层时密度又略微升高[9-11]，如图5a）所示。

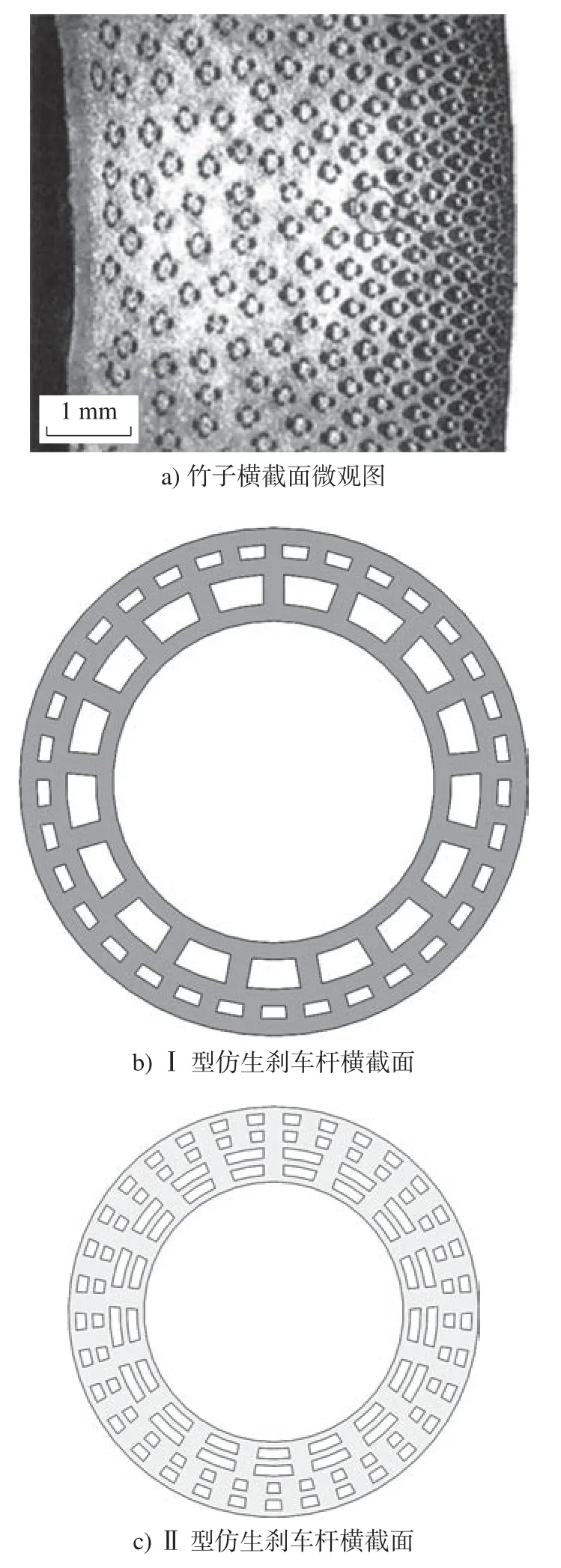
图5 竹截面和仿生结构截面Fig.5 Bamboo cross-section and bamboo-like structure cross-section

通过分析竹子横截面微观结构可知，起着承载作用的厚壁细胞外密内疏规律的镶嵌在由薄壁细胞组成的机体组织中，而承载的厚壁细胞与传递载荷的薄壁细胞良好的组合决定了竹子优良的力学性能，如图5a）所示。

基于竹子优异的力学性能特点，以截面积基本不变为基准，对圆形实体拉杆进行仿竹设计，如图5b）和图5c）所示为中空夹层结构的两种仿生设计截面，用一层套一层的具有一定厚度的圆筒模拟薄壁细胞组成的机体组织以传递载荷，圆筒之间的长方体支撑筋模拟有承载作用的维管束厚壁细胞，而长方体支撑筋与圆筒之间有相应的重合以模拟竹子的力学性能[12]。

3.2 对仿生上刹车杆的静力学分析

基于上刹车杆的加载方式，对Ⅰ型和Ⅱ型仿生拉杆进行静力学分析，结果表明：仿生结构在质量和单位变形量基本不变的情况下，最大应力降低50%左右，证明仿竹设计对结构有所改善。

4 响应面法优化

响应面法是通过显式的表达式以近似地表示隐式响应函数模型的方法，而响应面法优化则是基于响应面结果的目标驱动优化方式，即通过生成的响应面的结果自动寻找最优点近似的响应点作为最优解设计，该优化方法可以快速地搜索到候选最优解，但是也极其依赖于响应面生成的质量。

为了在满足强度及刚度的条件下得到最终内部结构的支撑筋、空腔深度和空腔截面直径的尺寸，利用ANSYS 中的响应面优化模块对中空夹层拉杆内部结构进行优化。

4.1 优化设计

如图6 所示，定义了Ⅰ型和Ⅱ型仿生刹车杆支撑筋的厚度尺寸、圆柱空腔深度尺寸以及圆柱空腔截面直径尺寸为设计参数，其原始值以及优化取值范围如表1 和表2 所示。其中，表1 为Ⅰ型仿生刹车杆设计参数，表2 为Ⅱ型仿生刹车杆设计参数。

表1 Ⅰ型仿生刹车杆设计参数Tab.1 Design parameters of type I biomimetic brake rod

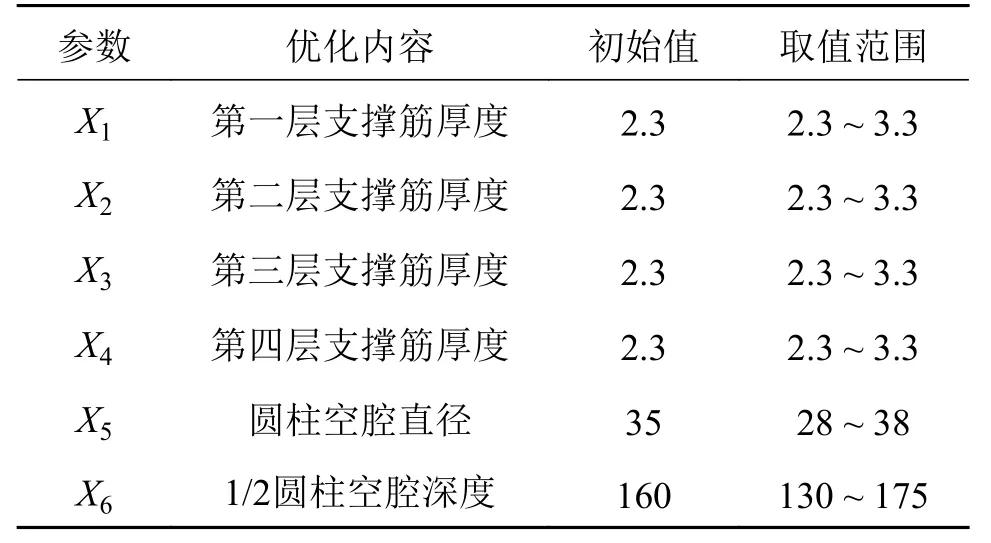
表2 Ⅱ型仿生刹车杆设计参数Tab.2 Design parameters of type Ⅱ biomimetic brake rod

图6 刹车杆设计参数的定义Fig.6 Definition of brake rod design parameters

本文中的优化模型是以结构质量最小化为优化目标，以结构的最大等效应力、结构的最大变形量为约束条件。考虑其安全系数，则拉杆的最大等效应力不应大于材料的许用应力，具体数学模型如下：

式中：X为设计参数；m（Xi）为质量；σ为结构等效应力；δ为结构变形量。

4.2 响应面优化分析

在进行响应面法分析之前，需要选择合适的实验点设计方法，常用的有空间填充设计方法、中心复合设计等方法。在本次实验中，对比了上述的两种实验点选取方法，发现在进行实验点取样时，空间填充设计方法所生成的样本点分布均匀，数量少，能够避免样本点的聚集，但是无法在端点附近取到满意的样本点，这会影响端点区域的响应面生成质量。进而采用中心复合设计方法进行试验样本点的设计，这是经典的样本点设计方法，使用较为广泛，其生成的设计填充点包含中心点、端点，并且通常加入轴点设计对取样进行了增强，以便于响应面生成过程中的弯曲曲面估计，能够适应复杂的响应面算法。

在ANSYS 中采用Kriging 函数构造响应面[13-15]。图7 为对结构最大等效应力和质量影响较大的两个设计参数的响应面图。

图7 各个函数响应面Fig.7 Response surfaces of functions

根据4.1 节的数学模型，最终仿生Ⅰ型和Ⅱ型刹车杆由响应面法分别获得了3 组最优解，如表3和表4 所示。其中，表3 为Ⅰ型仿生刹车杆3 组最优解，表4 为Ⅱ型仿生刹车杆3 组最优解。

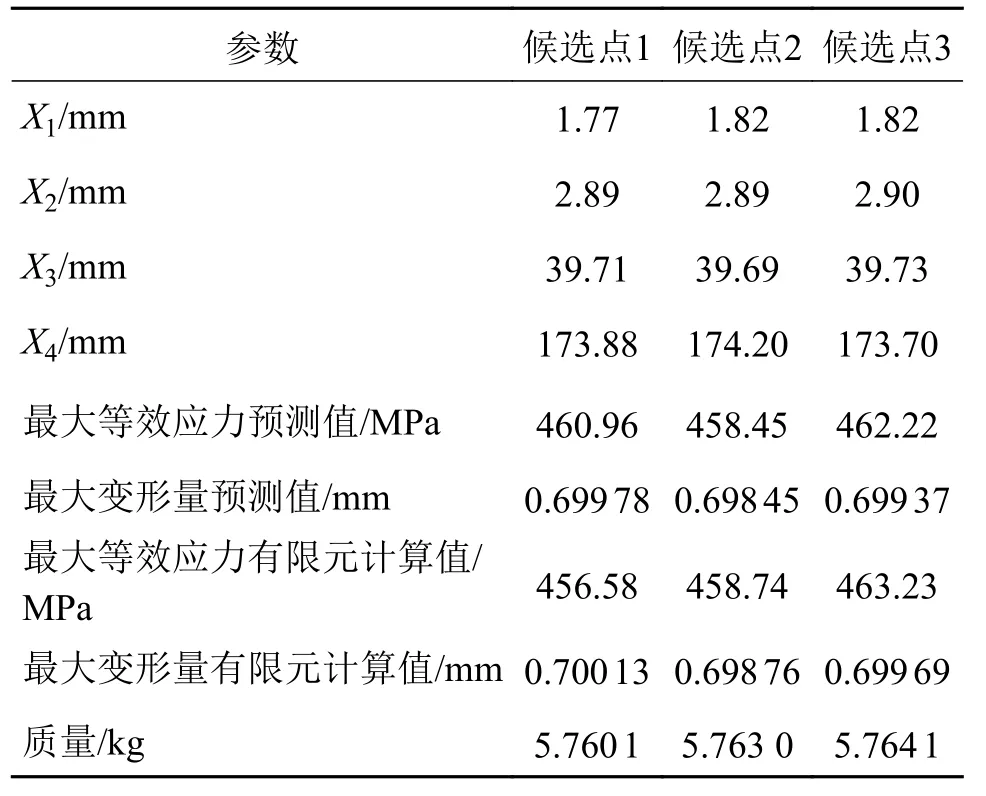
表3 Ⅰ型仿生刹车杆3 组最优解Tab.3 Three optimal solutions for Type I biomimetic brake rod

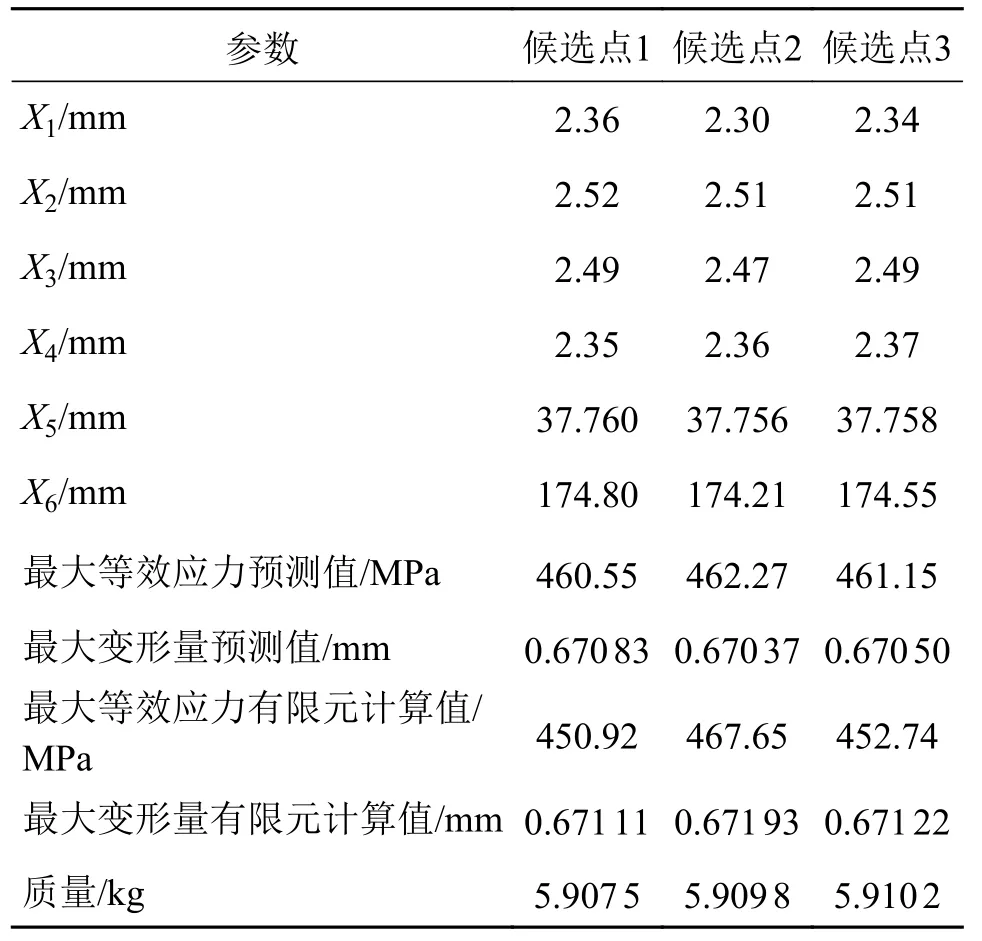
表4 Ⅱ型仿生刹车杆3 组最优解Tab.4 Three optimal solutions for Type Ⅱ biomimetic brake rod

由表3 和表4 可知：响应面法得到的最大等效应力预测值与有限元计算分析结果相比，误差在0.1%～2.0%，而最大变形量预测值与有限元计算分析结果相比，误差在0.04%～0.10%。误差极小，响应面法的预测精度较高，结果可靠。

通过具体对比，Ⅰ型仿生刹车杆选择候选点1为最终优化解，即X1＝1.77 mm，X2＝2.89 mm，X3＝39.71 mm，X4＝173.88 mm。Ⅱ型仿生刹车杆选择候选点1 为最终优化解，即X1＝2.36 mm，X2＝2.52 mm，X3＝2.49 mm，X4＝2.35 mm，X5＝37.76 mm，X6＝174.8 mm。图8 为优化后仿生刹车杆的横截面形状。刹车杆优化前后性能对比如表5 所示。

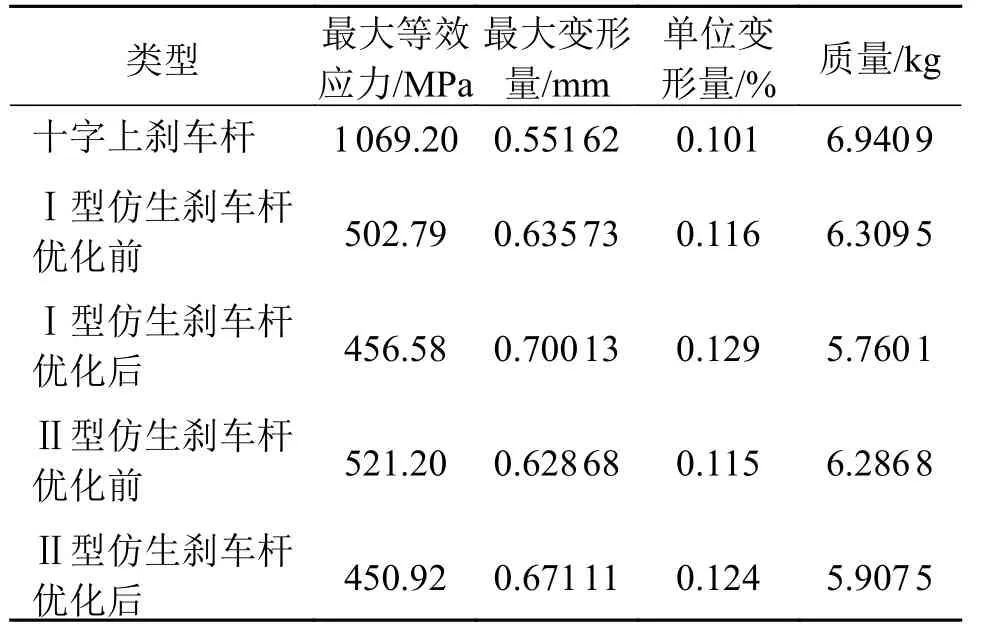
表5 刹车杆优化前后性能对比Tab.5 Performance comparison of brake rod before and after optimization

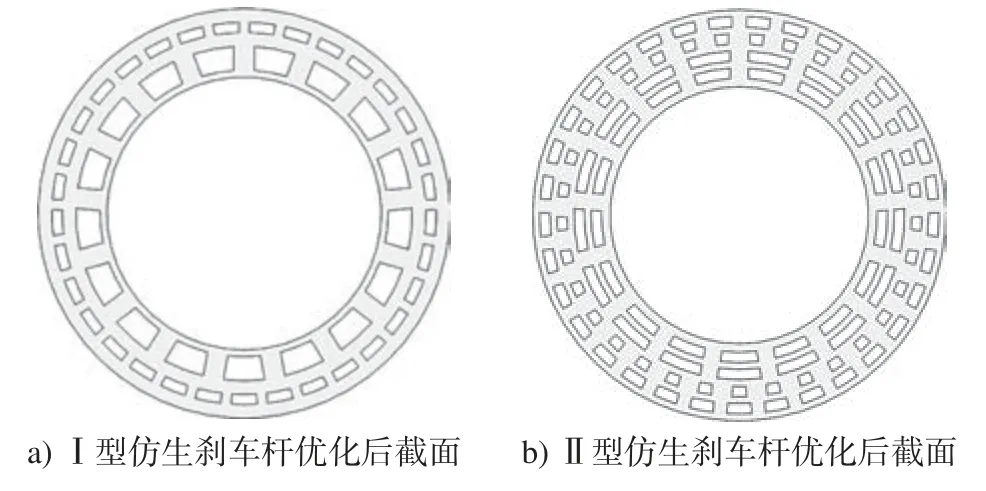
图8 优化后截面形状Fig.8 Cross-section after optimization

由表5 可知：在对圆形实体刹车杆进行了仿生结构优化设计后，质量下降比较明显且能满足强度要求。具体来说，两种仿生刹车杆相比于十字形刹车杆：仿生Ⅰ型刹车杆和仿生Ⅱ型刹车杆在危险处的最大等效应力值都有明显的降低，分别降低了57.34%和57.90%，二者的最大等效应力值接近；在刚度方面，仿生Ⅰ型和Ⅱ型刹车杆的最大总体变形量虽有所增加，但单位变形量基本不变，而且仿生Ⅰ型和Ⅱ型刹车杆的质量相比十字拉杆都有所降低，分别降低了17% 和14.98%。因为危险处的最大等效应力值都有较大安全系数的性能盈余，所以质量仍可根据实际要求进一步降低。

5 结论

对飞机刹车上拉杆进行了仿竹结构改进，并采用响应面法对相关参数进行了优化，得到结论：

1） 圆形中空仿竹结构刹车杆可大大降低最大应力值，避免危险处应力集中现象。

2） 应用了响应面法优化对结构进行详细设计，通过响应面法进行参数优化，可进一步提高优化效果。

3） 仿竹结构内部结构复杂程度对优化结果影响不大。

4） 适当加大中空结构长度，对降低最大应力是有利的。

本文由于变量较少，未进行敏感度分析，如果变量较多，可利用参数敏感度分析进行参数筛选，以简化计算。本文研究结果对飞机杆件结构的设计有重要的实际意义，可在结构轻量化及参数优化中推广使用。