LTCC 基板微通道进出口布局结构散热性能仿真分析*

廖志平，罗冬华

（桂林信息科技学院机电工程学院，广西桂林 541004）

0 引言

智能电子产品需求的日益增长推动了电子产品向小型化、多功能化、高可靠性等方向发展，与此同时带动了电子封装技术向更高集成化、更高可靠性的方向发展。目前大多数电子装备在工作过程中对温度条件是异常敏感的，若长期在过热的环境下工作会使得器件热应力分布不均匀，导致设备故障或者失效[1]。然而随着组装密度的不断增加，电子封装器件的热流密度也随之不断上升，电子装备散热问题日益凸显，如未来雷达等高可靠性装备用的微波TR 组件热流密度预计突破1 000 W/cm2，而目前TR 组件的散热能力仍然较弱[2]。传统的封装技术很难满足耐高温、高密度、高可靠性等的要求，更先进的封装技术与更多的高可靠封装材料应运而生。微通道流体散热技术近年来受到了广泛的关注与青睐[3]，为解决大功率组件散热问题提供了新的方案。低温共烧陶瓷（LTCC）因其耐高温、稳定性好、成本低、热匹配好等特点被广泛应用于高密度、高可靠性的微波射频TR 组件的封装中[4]。

微通道的横截面尺寸、流体进出口位置布局、流体进出口尺寸等结构都会影响其散热特性。本文结合基于LTCC 的TR 组件的散热需求，采用数值仿真分析方法重点研究微通道流体进出口布局结构对组件散热性能的影响，进而优化结构参数，为实物设计提供依据。

1 理论基础

1.1 热传导

傅立叶定律提出，热传导基本规律表示为特定面积的热流量，其传导的热流量与温度梯度方向的截面积成正比[5]。热流量Q 可表示为

其中，λ 表示材料的热传导系数，A 表示垂直于热传导方向的截面积，表示温度梯度。

1.2 热对流

微通道中的流体各部分产生的宏观相对运动将会引起热量的传递。根据牛顿冷却公式，热流密度q 可以表示为

其中，h 表示对流换热系数，tw-tf表示流体与接触冷却物体的温差。

采用LTCC 作为基板的微波TR 组件中微通道换热属于强迫对流换热，因此可以将其用外掠平板层流换热模型简化。h 可以用公式（3）（4）求出。

其中：b 表示LTCC 组件传热面积；Re 为雷诺数；Pr表示普朗特准则，Pr=μCp/λ，无量纲数群，反映流体物性对换热系数的影响，μ 表示黏度系数，Cp表示流体的比热容；Nu表示努赛尔准则，Nu=hl/λ，无量纲数群，反映对流换热过程的强度。

1.3 热-流耦合

在微纳尺度模型中，宏观的流体动力学中被忽略的一些力将会起到一定作用，比如流体的表面张力以及流体分子极化后的范德华力等，这些分子间的作用力属于短程力的范畴（＜1 nm），这些作用力累积后仅仅可达到约1 μm 的长程[6]，远小于TR 组件中微通道的尺寸范围，因此所示的宏观流体动力学的3 个方程依然适用。

a）连续性方程：

b）动量守恒方程：

c）能量守恒方程：

其中，υx、υy、υz表示流体在x、y、z 方向上的速度，P 表示压强，表示流体在x、y、z 方向上的压强梯度，X、Y、Z 表示流体微元受到的体积力，ρ 表示流体的密度，T 表示流体温度。

根据流体动力学方程，如果得到基于LTCC 的TR 组件微通道内部分流体的温度以及x、y、z 3 个方向的压强、流速，就可获得微通道中流体的温度、压强、流速的分布情况，从而获取整个TR 组件结构的温度。

2 LTCC 微通道进出水口结构有限元建模

2.1 基于LTCC 的TR 组件模型建立

本文建立了基于LTCC 的微波TR 组件三维模型，该模型由单层厚度为0.127 mm 的25 层LTCC 生瓷片通过层压工艺形成，模型长为45.000 mm，宽为45.000 mm，总厚度为3.175 mm，底部放置了长2.000 mm、宽1.000 mm、厚0.100 mm 的8 行8 列的大功率芯片。功率芯片通过导电胶与LTCC 基板互连。微通道散热结构位于LTCC 基板内部，2 条主流道，截面尺寸为2.200 mm×0.760 mm，长38.000 mm，进出水口均位于主流道上，为柱形；微通道的次流道分为8条，截面尺寸为2.000 mm×1.000 mm，平行排列在主流道上。大功率芯片排列在其上面，每条通道排列8 个芯片，通道截面呈长方形，通道长度为38.000 mm。微通道主流道与次流道分别制作后堆叠成型，主流道在次流道上方连通，经层压工艺使得微通道在LTCC 内成型，组件截面形状如图1 所示。

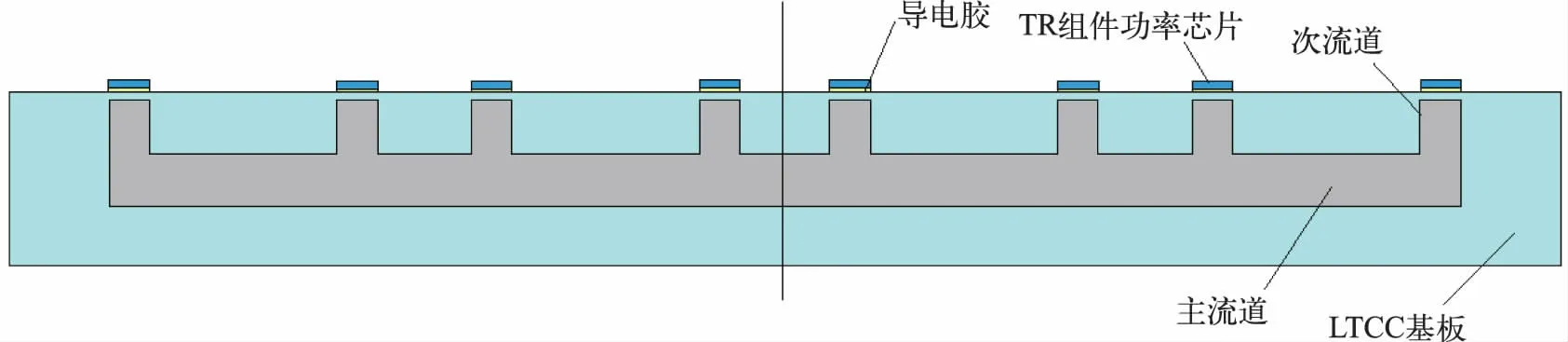
图1 LTCC 微通道截面形状

2.2 流体进出口结构建立

根据建立的LTCC 微波TR 组件三维结构模型，设置了4 种不同进出水口布局结构方式，分别为对角方式、中间方式、侧边方式及中间-侧边方式，如图2所示。

图2 微通道流体进出口布局结构

2.3 有限元仿真设置

TR 组件主要包括LTCC 基板、微通道、大功率芯片以及互连结构等，这些部分都与组件散热相关，各部分材料参数如表1 所示。

表1 各部分材料及相关参数

利用ANSYS 有限元数值仿真是获得TR 组件微通道散热模型的有效方法。由于组件的结构复杂性与仿真分析计算效率等因素，在不影响模型仿真结构准确性的前提下对结构进行一定的简化处理，设置合理的边界条件，并进行如下假设：

1）微通道内的流体为稳态流动、流体层流流动不能压缩，局部的紊流现象可忽略（根据计算，132

2）壁面无滑移边界条件、N-S 方程依然适用；

3）热辐射对散热的影响小，忽略热辐射散热；

4）流场分布稳定；

5）热传输过程稳定。

3 结果分析

3.1 微通道进出水口布局结构对组件温度的影响

从仿真结果分析，组件在不同方式下的整体温度分布有明显的差异。微通道进出口布局结构对组件温度的影响如图3 所示。从TR 组件整体来看，4 种方式中组件的最低温度均出现在进水口处，温度基本呈梯度分布，且进水口处与出水口处温差很大。最高温度均出现在靠近出水口处的大功率芯片处，出现局部热量集中现象。

图3 微通道进出口布局结构对组件温度的影响

对角方式中的组件芯片最高温度约为53 ℃，组件四周温度较低，与进水口相连的主流道温度最低，整体热量大部分集中在组件中间靠下部分，组件整体热量分布不均，热量比较集中。中间方式进出口布局结构中进水口处主流道周围温度最低，温度从进水口处往出水口处逐渐升高，热量分布均匀，最高温度出现在出口附近，约为50 ℃，没有出现明显的热量集中现象。在侧边方式进出口布局结构中，TR 组件最低温度点出现在进水口处，最高点位于右下边角的功能芯片上，最高温度约为56 ℃，热量集中在右下角区域。中间-侧边方式结构中组件整体热量分布不均，热量集中在左下角部分，温度最低部分位于进水口所处的主流道周围，组件最高温度约为52 ℃。由此可见，中间方式相对其他3 种方式而言，其结构热量分布较均匀，温度分布也较为均匀，整体温度最低，散热性能较好。

3.2 不同进出口布局结构压力损失分析

设计微通道还应考虑通道内流体的压力损失，4种布局结构的压力场分布云图如图4 所示。从整体来看，4 种方式通道内的压强在进水口周围最大，在出水口周围最小，压强沿着进水口至出水口方向基本呈梯度变化，中间-侧边方式结构中左上角部分出现了压强分布不均现象，其他3 种方式压强分布相对均匀。中间方式中，组件微通道内流体的压强最大处位于进水口，沿进出口方向基本呈左右对称分布，流体压强分布相对均匀，而且该方式中流体的压强损失也最小，约为0.04 MPa；其他3 种方式中，流体压强分布均匀性较差，压强损失大，中间-侧边方式压强损失约为0.07 MPa，侧边方式压强损失约为0.08 MPa，其中压强损失最大的是对角方式，约为0.10 MPa。

图4 不同进出口布局结构组件微通道内流体压强分布

综合前面的仿真结果，组件微通道中间方式的进出口布局结构与其他3 种方式相比较优。

4 结论

本文根据基于LTCC 的TR 组件结构的散热特点，采用ANSYS 有限元仿真分析软件对组件微通道4种进出口布局方式结构的散热性能进行了数值仿真研究，并获得了组件在一定条件下的热流场、压力场的仿真分布云图，总结得到以下结论。

1）在数值仿真边界条件一致、组件芯片功率相同的情况下，对基于LTCC 的TR 组件微通道进出水口4 种布局结构进行有限元仿真分析，结果表明采用中间方式的微通道进出口布局结构，TR 组件的整体热量分布较均匀，功率芯片最高温度约为50℃，没有明显的热量集中，综合散热性能相对其他3 种方式为最佳。

2）从有限元数值仿真结果可以看出，4 种微通道进出水口布局结构中流体在进水口处的压强最大，在出水口处的压强最小，压强沿着进出水口方向大致呈梯度变化。中间-侧边方式布局结构相对其他3 种方式有较为明显的压强分布不均现象，压强损失较大，中间方式进出口布局结构中微通道内流体的流速、压强分布相对其他3 种较均匀，整体的压强损失最小。