电动汽车电驱动系统容性轴电压建模研究

2024-04-03于建寅

微特电机 2024年3期

于建寅,朱莉,黄超,龚宇

(1.上海交通大学电子信息与电气工程学院,上海 200240; 2.同济大学汽车学院,上海 201804;3.舍弗勒贸易(上海)有限公司,上海 201804)

0 引言

随着电动汽车普及率提高,其驱动系统轴电压的危害也日益得到重视。驱动逆变器的开关频率和车用电机电压等级的提高都增加了共模电压脉冲的陡峭程度,使其更加容易通过电机各部分的寄生电容,在系统回路中产生破坏性电流[1-3]。因此,电动汽车轴电压研究受到了越来越多的关注。

单交流电机的高频电路模型陆续被提出[4-7],该方法利用类似的模型,将实测的共模电压作为激励,对轴电压进行预测[8-9]。然而,电驱动系统作为电动汽车中一个系统级部件,其设计制造与自身各模块密不可分。另一方面,电动汽车作为需要量产的产品,应尽量减少每个产品的实验步骤,而采用实测共模电压作为激励进行高频模拟的方式将加大实验的时间和成本。因此,需要考虑系统级仿真模型,以更低的成本和更高的效率对电驱动系统进行评估[10]。

本文基于高频和低频电路的特征,考虑将其分离建模,提出了一种车用电驱动系统的仿真模型,旨在建立一种无需通电,仅通过建模仿真就能预测电动汽车驱动系统轴电压的新方法。该方法既能保证精度,又避免了现有方法对系统通电运行的步骤。本文模型分为低频的控制模块和高频的共模回路模块两个部分。其中,电机的电路模型采用了集总参数和高频参数两种方式,分别应用在电机控制模块和共模回路模块中。控制模块采用传统的转子磁场定向控制方案,本文不作详述。共模电压在电机控制模块中提取,并同时作为共模回路模块的激励,这降低了仿真所需要的时间。此外,针对电动汽车电驱动系统的特殊结构,考虑变速箱对轴电压的影响,对其进行了建模,并集成于系统模型中。最后,本文将仿真结果与270 V、120 kW电动汽车电驱动系统的实验结果进行了比较。

1 高低频分离型轴电压仿真

电机定子三相绕组的中性点对地电压为共模电压[6]。但对于系统级仿真,电机控制回路的频率远低于共模回路的频率,直接将共模回路从定子绕组中性点连出将会产生较大的误差。

图1为常规带有共模阻抗的简化电机电路模型。

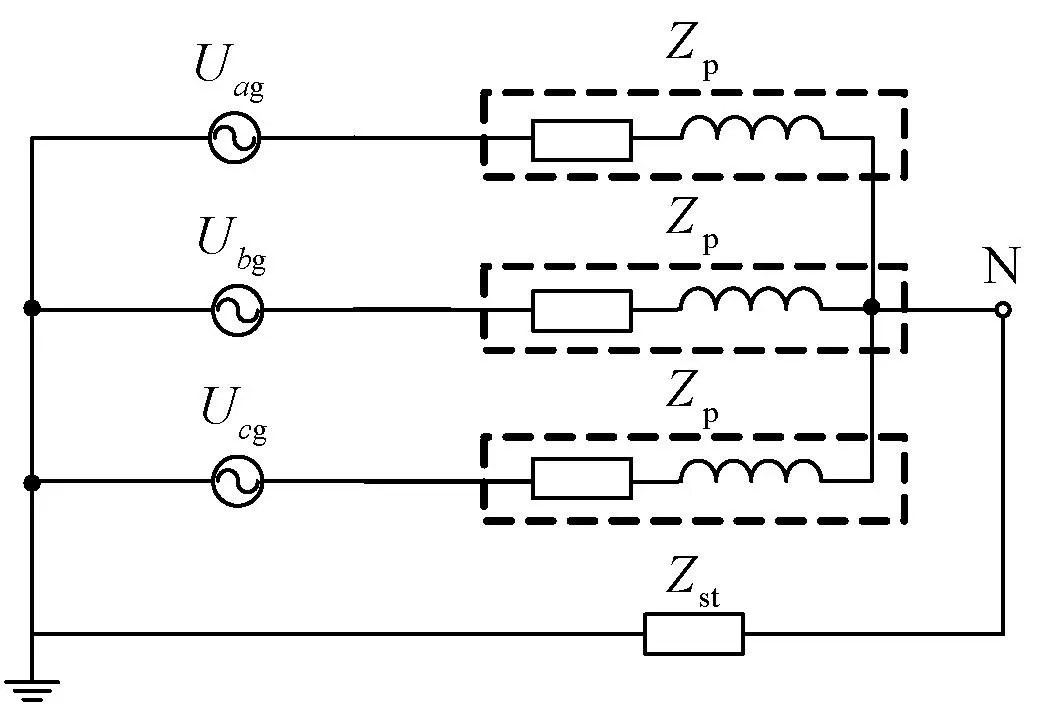
图1 考虑共模阻抗的简化电机控制电路

Uag、Ubg、Ucg分别表示三相对地电压;Zp表示定子每相阻抗;Zst表示共模回路的等效阻抗。对节点N列写节点电压方程,可得节点N的电压表达式:

(1)

相阻抗Zp由定子相电阻和相电感组成,而共模回路阻抗Zst主要由电容值较小的寄生电容组成。随着频率的升高,Zp与Zst的变化完全相反。Zp中的相电阻对阻抗的贡献不变,相电感的感抗不断增大,使得Zp整体增大。Zst中电容的容抗不断减小,使得Zst整体减小。于是,在低频工况下,Zp很小,Zst很大,Zp/Zst的值非常小,可以忽略不计;而在高频工况下,Zp/Zst的值较大,若忽略该比值,节点N的电压与共模电压会产生较大的偏差。

为了避免该问题,考虑将高频电路与低频电路分离,简图如图2所示。

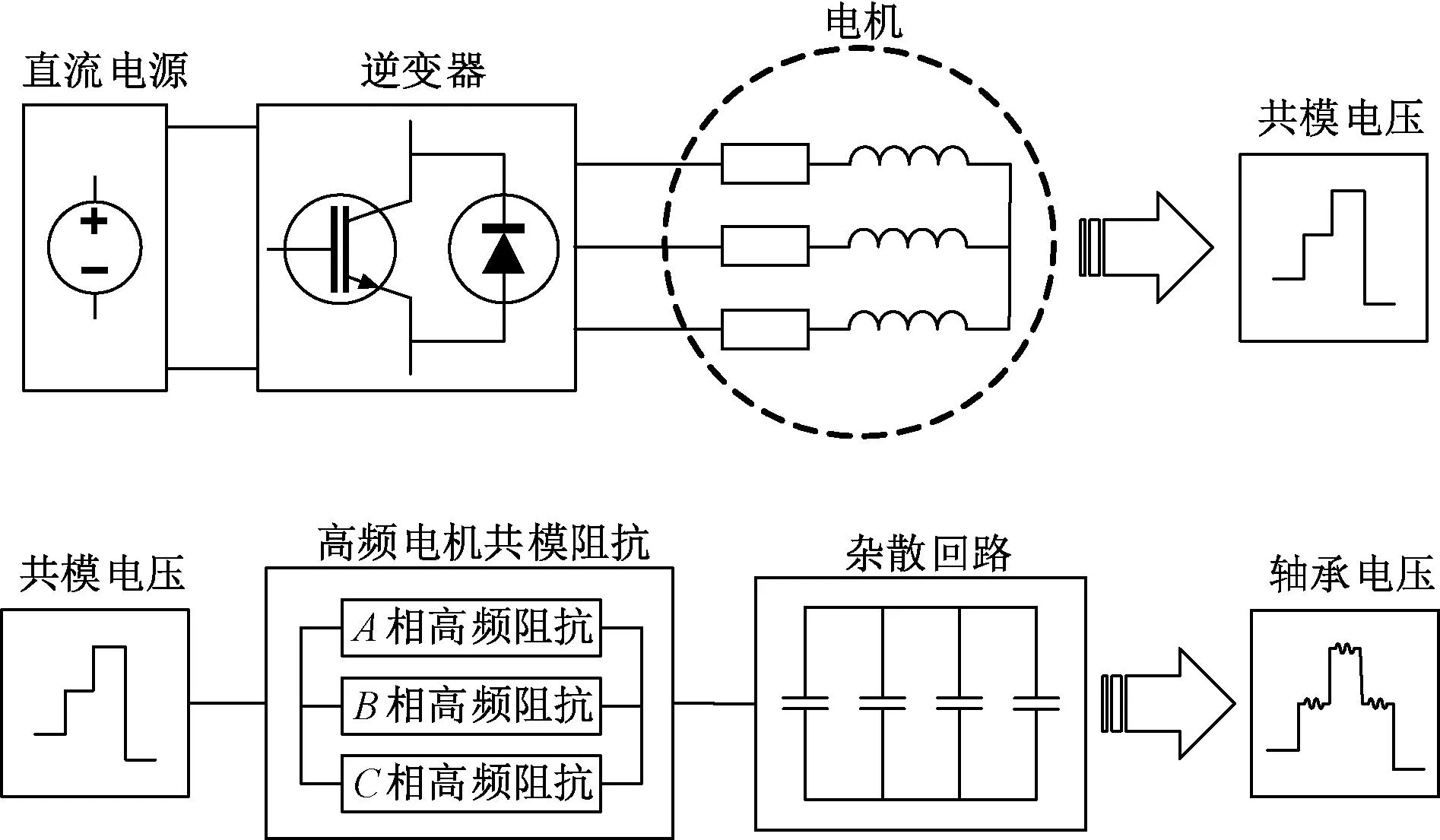
图2 分离型仿真模型

从低频回路中将共模电压提取出来,并作为高频回路的激励,有效降低了高频共模阻抗对节点N电压的影响,从而减小了仿真结果的误差。

2 共模回路模型

2.1 电机模块

文献[11]给出了仿真结果非常精确的电机高频模型及参数提取方法,但其需要用阻抗分析仪测量定子绕组的共模和差模阻抗曲线、转子对机壳阻抗曲线、轴承阻抗曲线,然后通过联立各端口阻抗表达式求解参数。该方法操作较为复杂,易受到设备限制。

本文构建了一个定子绕组高频简化模型,模型如图3所示。该电路模型足够简单,但包含了必要的元素,仅需要定子相绕组对地阻抗曲线和简单计算,便可完成所有参数的提取。

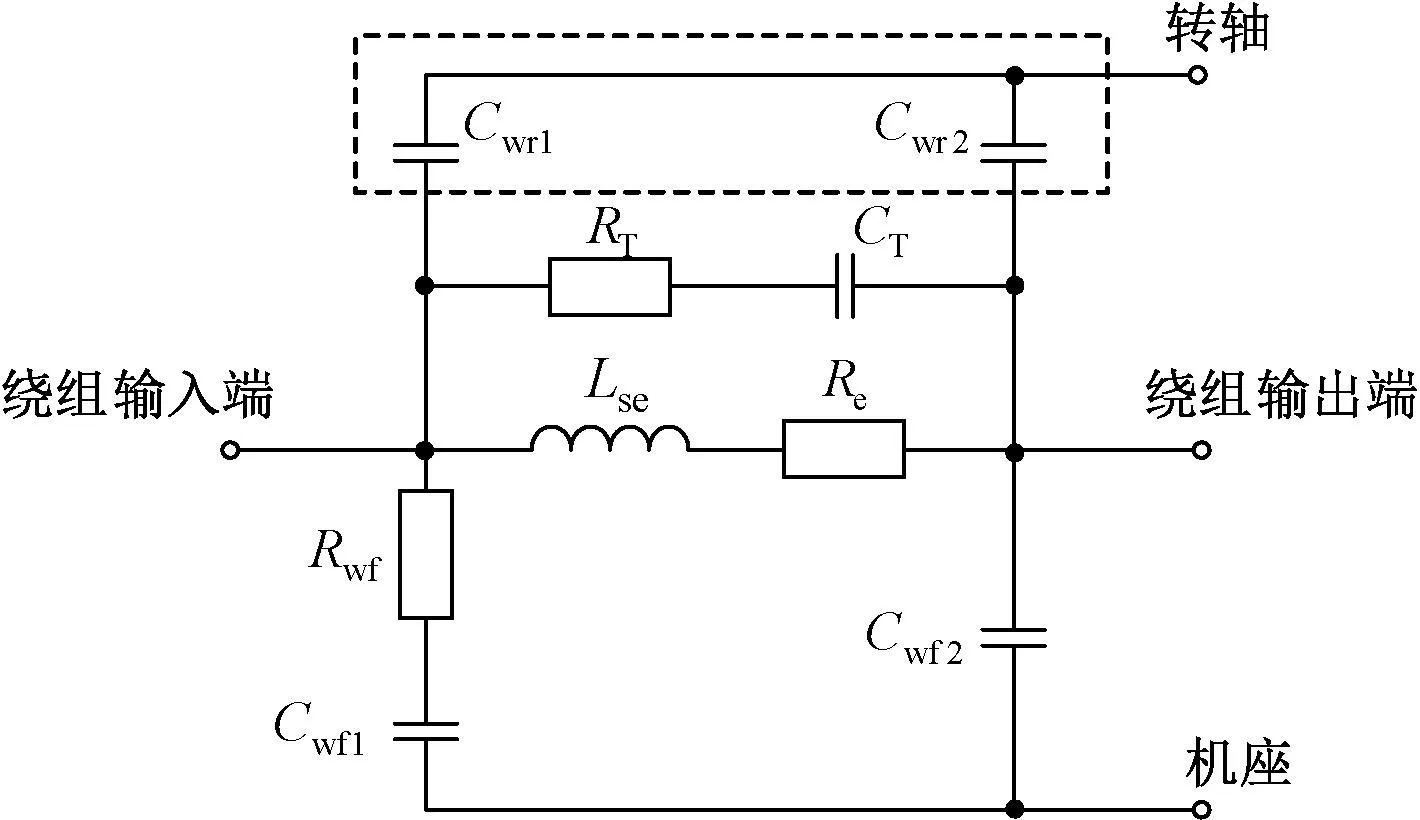
图3 定子单相绕组高频简化模型

电路中包括相绕组电感Lse,涡流损耗电阻Re,匝间电阻RT和匝间电容CT,绕组与定子机壳之间的寄生电容Cwf1、Cwf2和寄生电阻Rwf。虚线框中为绕组与转子之间的寄生电容Cwr1、Cwr2,需要在上述参数完成提取后单独计算。Cwf1和Cwr1分别代表高频段的部分。本文将基于270 V、120 kW电动汽车电驱动系统实验平台,详细介绍其参数提取方法。

图4为采用Bode100测量的电机单相绕组的阻抗、相位与频率关系曲线。图4中标注了5个关键节点。节点的频率、阻抗和相位如表1所示。

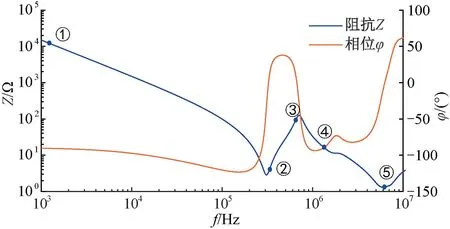
图4 单相绕组的阻抗、相位与频率关系曲线

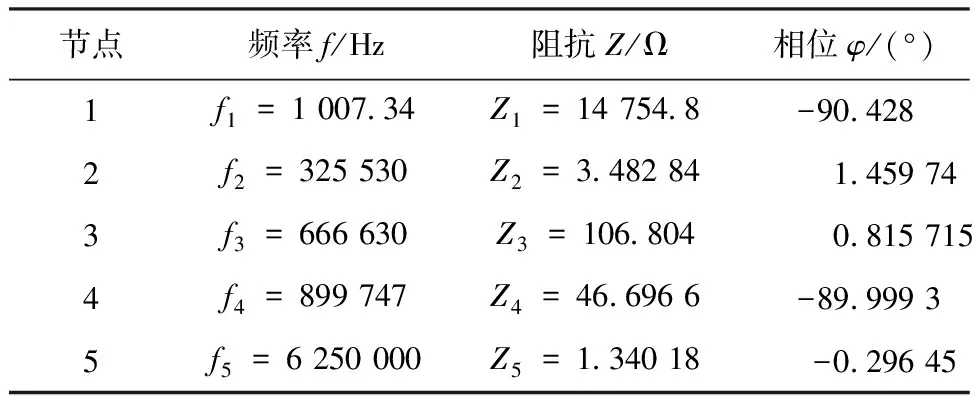
表1 关键节点的频率、阻抗和相位

节点1是低频下相位最接近-90°的点,此处阻抗贡献全部来自于绕组与定子之间的寄生电容Cwf,该电容值可以由该节点的阻抗Z1和频率f1计算:

(2)

Cwf表示绕组与定子之间的总寄生电容,可以由下式表示:

Cwf=Cwf1+Cwf2

(3)

计算得Cwf=10.7 nF。

节点2是中低频段相位最接近0°的点,此时绕组电感Lse与电容Cwf串联谐振,阻抗近似等于涡流损耗电阻Re,故Re=3.48 Ω。由串联谐振可得:

(4)

计算得Lse=22.3 μH。

节点3是中频段相位最接近0°的点,该处绕组电感Lse与匝间电容CT发生并联谐振,阻抗近似等于匝间电阻RT,故RT=106.8 Ω。由并联谐振有:

(5)

计算得CT=2.55 nF。

节点4是中高频段相位最接近-90°的点,可近似认为阻抗均由Cwf1贡献。Cwf1可由阻抗Z4和频率f4计算:

(6)

计算得Cwf1=3.79 nF。再根据式(3),计算得到Cwf2=6.91 nF。

节点5是高频段相位最接近0°的点,此时阻抗分析仪引线的漏感不能忽略,且与高频电容Cwf1发生串联谐振,故该点的阻抗值等于绕组与定子之间的寄生电阻Rwf,即Rwf=1.34 Ω。可以通过该点的频率及电容Cwf1计算阻抗分析仪的漏感。基于图3的模型和提取的参数,仿真计算出阻抗曲线,与图4进行比较,对比结果如图5所示。

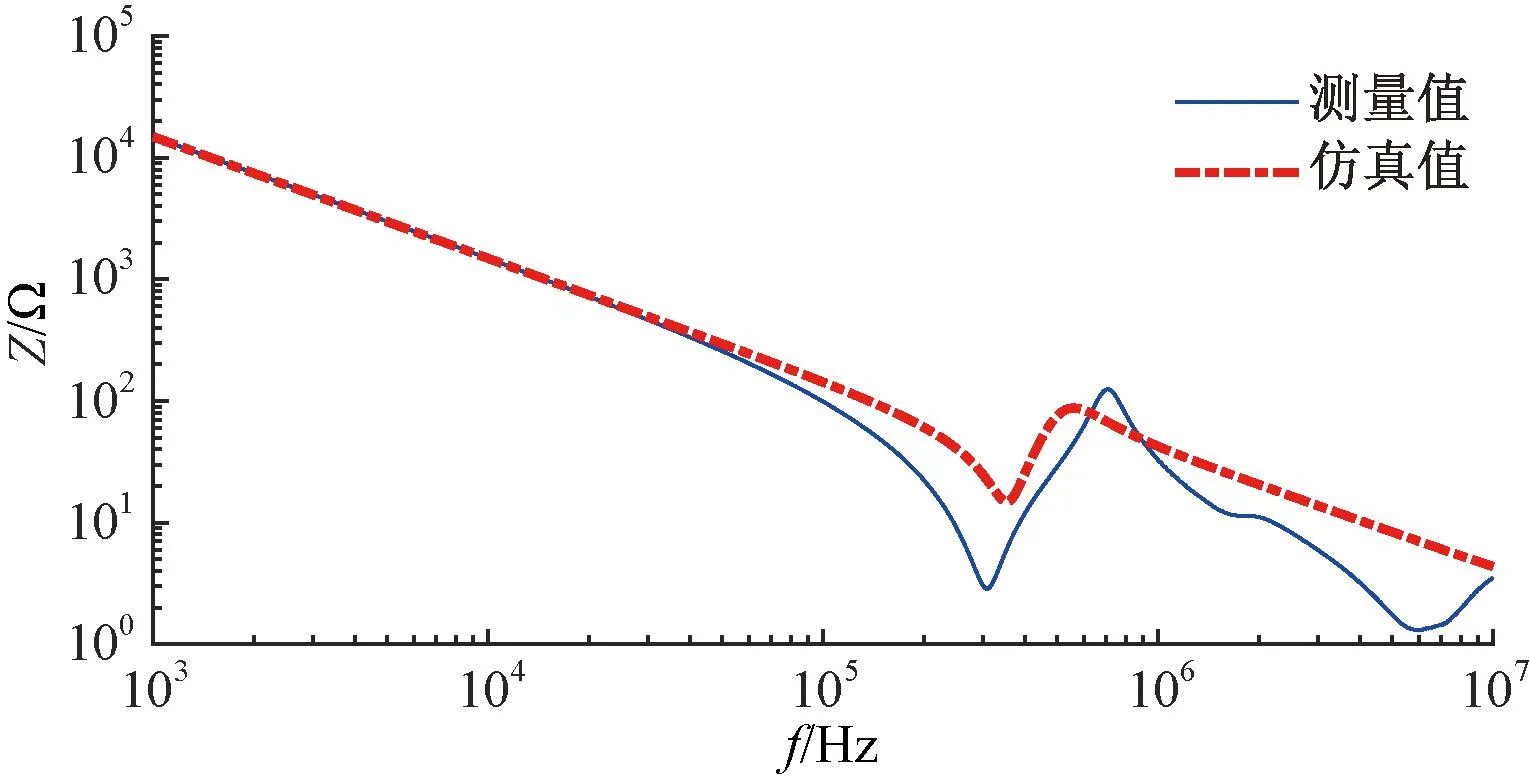
图5 单相阻抗仿真结果对比

仍需确定的参数还有Cwr1和Cwr2。与式(3)相同,绕组与转子之间的总寄生电容Cwr可用下式表示:

Cwr=Cwr1+Cwr2

(7)

绕组与转子之间的总寄生电容Cwr可以通过电机的几何尺寸或有限元法计算。绕组与转子之间的总寄生电容Cwr可分为槽内绕组与转子铁心之间的电容Cwr_lam和端部绕组与转轴之间的电容Cwr_end。两部分电容为并联关系,故Cwr还可以由下式表示[12]:

Cwr=Cwr_lam+Cwr_end

(8)

Cwr_lam可由平板电容的计算公式导出,Cwr_end可由圆筒电容的计算公式导出:

(9)

(10)

式中:Qs表示定子槽数量;b0表示槽开口宽度;lFe表示铁心长度;h0表示槽开口高度;lendw表示绕组端部长度;Rendw表示绕组下底面所在圆周的半径;Rshaft表示轴半径;εr表示空气的相对介电常数;ε0表示真空介电常数;δ表示气隙长度。具体参数值如表2所示。

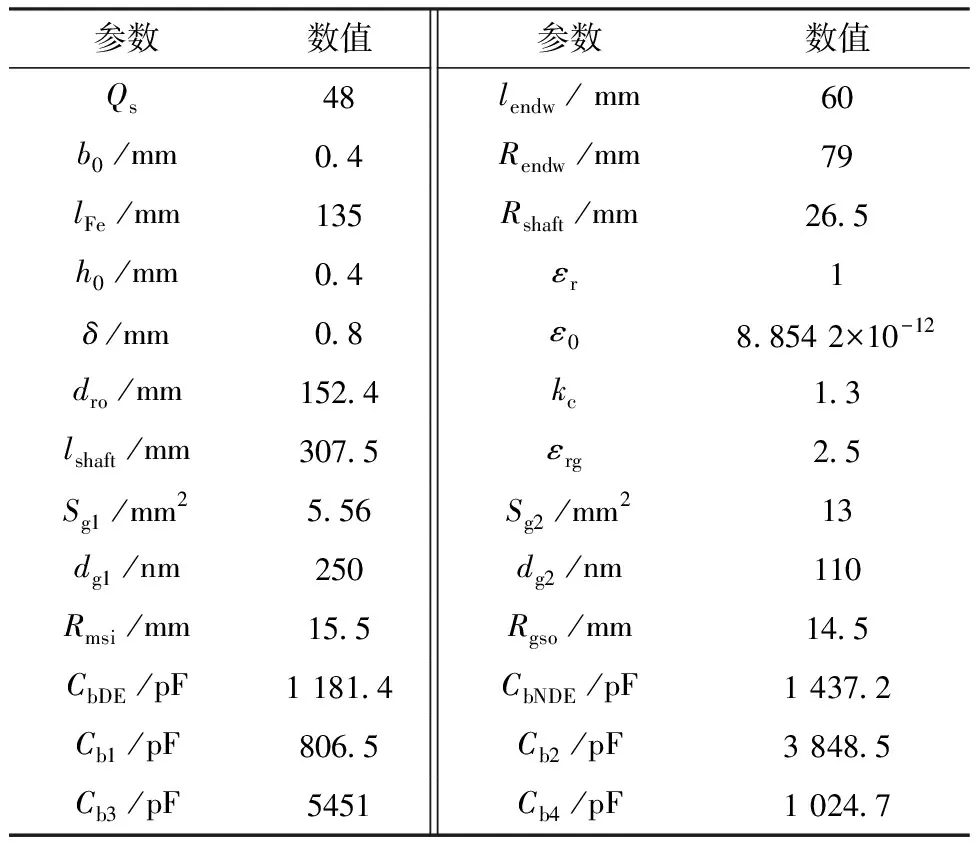
表2 电机参数

计算得Cwr=23 pF。

由于Cwf和Cwr在高频电机的电路模型中是对称的,根据文献[13],假设它们的两部分是成比例的,则:

(11)

式中:k表示Cwf和Cwr的高频段部分与它们自身的比值。由式(11)可以计算出Cwr1=8 pF,Cwr2=15 pF。

基于图3,可得完整的共模电路模型,如图6所示。

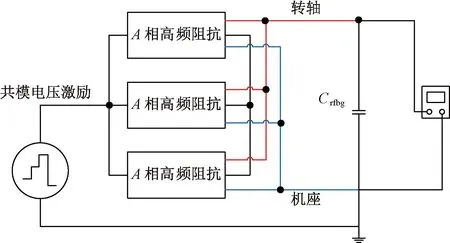
图6 完整的共模电路模型

其中,共模电压信号从低频控制电路中提取。三相共模高频阻抗由图3的三个单相阻抗并联得到。假设油膜未被击穿,将电机轴与机壳之间的电容Crf、轴伸端电容CbDE、非轴伸端电容CbNDE、变速箱电容Cgb合成为一个等效电容Crfgb,以简化分析。

Crf可以通过下式计算:

(12)

式中:dro表示转子外径;kc为卡特系数。参数值如表2所示。

计算得Crf=550 pF。

2.2 变速箱模块

本文研究的电动汽车驱动系统采用了同轴变速箱的传动结构。该变速箱实现两级变速,齿间采用润滑脂润滑。基于这种结构,得到变速箱的传动简图,如图7所示。

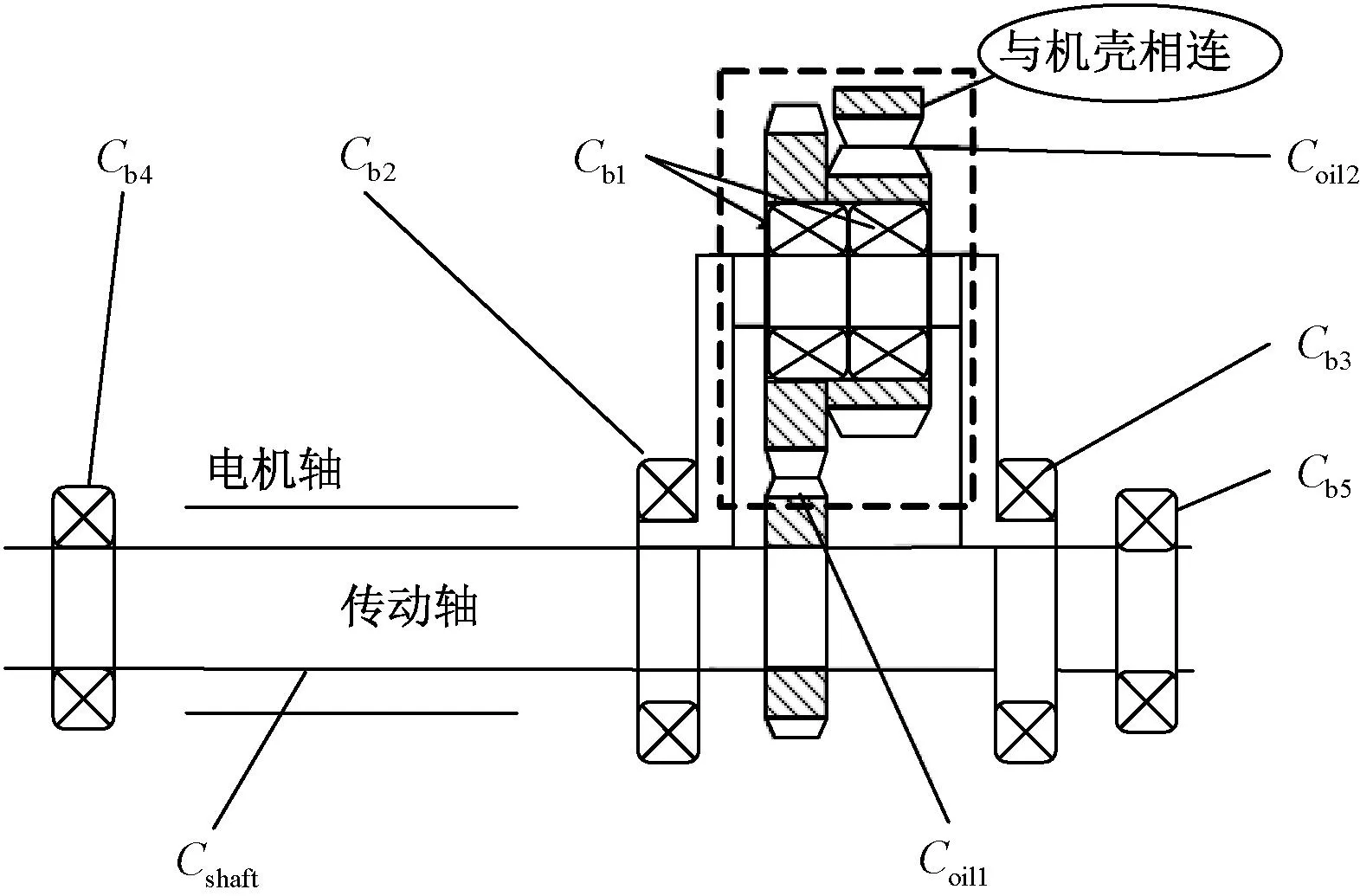
图7 变速箱传动简图

虚线框内为行星轮,一共有三个。变速箱采用了复数种类的轴承,简图中同种轴承的下标相同。齿轮的啮合点可以看作一个平板电容,表示为Coil1和Coil2,通过式(13)计算。所有轴承均与机壳相连,轴承本身也可以被视为电容器。此外,传动轴从电机轴中心穿过,两者之间为圆筒电容器用Cshaft表示,由式(14)计算。

(13)

(14)

式中:εrg为油脂相对介电常数;Sgi为齿轮啮合面积;dgi为齿轮啮合平均间隙;lshaft表示电机轴的长度,Rmsi表示电机轴内半径;Rgso表示传动轴的外半径。基于270 V、120 kW电动汽车电驱动系统实验平台,1 000 r/min、50 N·m工况,上述参数值如表2所示。

计算得Coil1=0.492 nF,Coil2=2.62 nF,Cshaft=0.257 nF。

如此,变速箱的电路模型可以简化为几个电容的串并联,如图8所示。

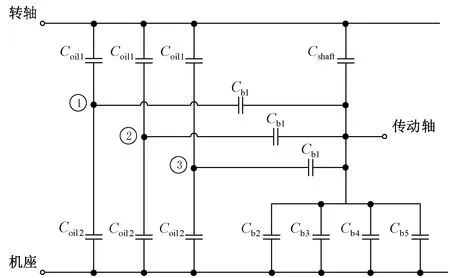
图8 同轴变速箱电路图

图8中,由于电路的对称性,节点1、2、3的电势相同。于是,变速箱的电路模型又可以进一步简化为如图9所示的形式。

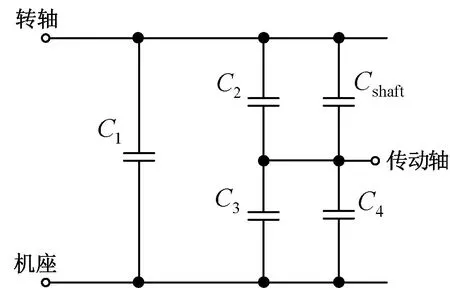
图9 简化的同轴变速箱电路图

因此,齿轮箱电容可以通过式(15)计算,电机轴和传动轴对地的分压比SVR可由式(16)计算。

(15)

(16)

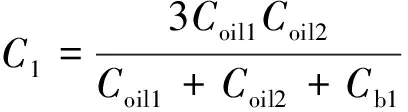
计算得到SVR=0.044。由于C2、Cshaft远小于C3、C4,故C2、Cshaft对SVR的值有决定性影响。结合式(15)和式(16)可得:

Cgb=C1+(C3+C4)SVR

由于SVR很小,Cgb的大小取决于C1,故齿轮啮合面油膜电容的大小起决定性作用。

3 测量与仿真

为了验证本文建立模型的准确性,搭建了电动汽车用120 kW负载测试台架,如图10所示。其中,IGBT的开关频率为10 kHz,直流母线电压为270 V,电机运行工况为1 000 r/min,50 N·m。在采用同轴变速箱的结构中,输出轴为变速箱的传动轴。输出轴通过绝缘联轴器与负载相连,以免负载影响驱动系统的接地状况。将碳刷固定在刚性平台上,保证其与电机轴能够充分且稳定的接触。

图10 负载实验台架

实验中,测量碳刷采用Aegis公司的SHAFT VOLTAGE PROBE型号;测量和记录轴电压波形采用LeCroy公司的WaveSurfer 10示波器。

仿真模型低频回路中的电机参数包括极对数p,相绕组电阻Rs,相电感Ls及互感Lm,相漏感Lσ,磁链ψ,数值如表3所示。

表3 低频电机参数

仿真和测量结果对比如图11所示。

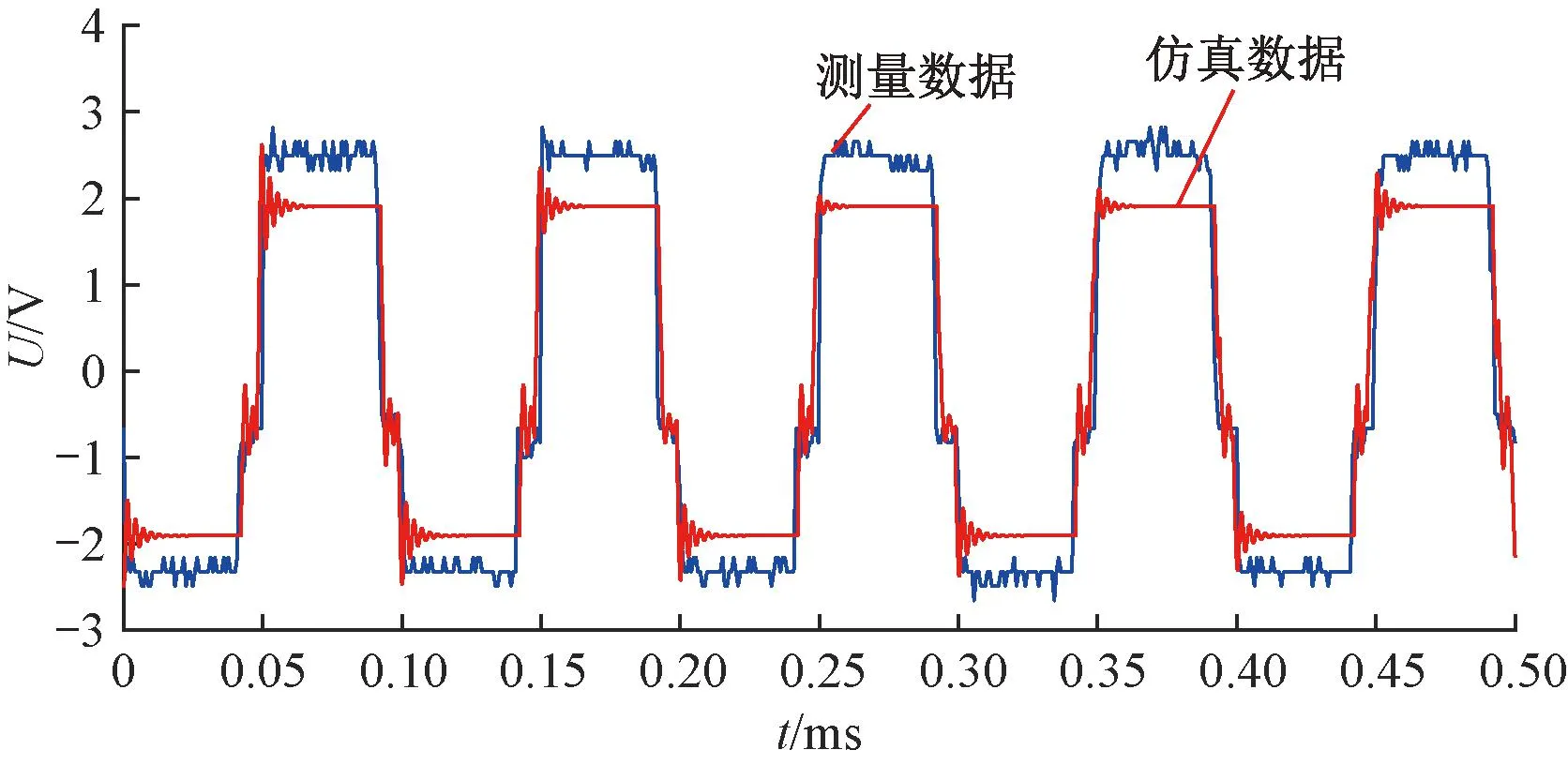
图11 轴电压测量和仿真波形

由图11可知,仿真得到的轴对地电压波形和测量波形吻合,幅值略小于测量值。其原因在于,为了减小传统轴电压仿真估计的难度和时间,系统模型较多地采用了提出的理论模型和计算结果。由对比可见,本文的电动汽车驱动系统的轴电压模型和建模方法无需复杂的实验和参数提取,可为实际轴电压分析提供一种更加便捷可靠的新方法。