基于特征匹配的激光雷达和相机外参标定方法

陈美林，蒋国涛，皮志超，贺 谦，谭 斌，罗 朔，阳海浪

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

传感器作为能够获取车辆周围环境信息的设备，在智能驾驶领域有着重要的地位。激光雷达能探测三维环境中目标物的空间信息，具有测距精度高、测量范围大等优点，但无法提供被探目标的颜色和纹理信息；相机可获取被探目标的颜色和外观等较为丰富的语义特征，但探测精度受光照及其他自然条件的影响较大。为克服单传感器探测的局限性，智能驾驶系统通常采用相机和激光雷达等多传感设备实现对环境的感知，通过这些传感器数据的同步融合，发挥各个传感器的优势，提高目标识别的可靠性［1］。其中传感器的外参数标定是数据同步融合的关键［2］。

激光雷达和相机的外参数标定本质是获取传感器坐标系间的转换关系，将点云数据和图像数据在空间上准确地对应起来。这种转换关系包括6个自由度，可由旋转矩阵和平移矩阵表示。目前，外参数标定方法主要包括基于标定板几何特征的方法［3-4］和基于环境特征的方法［5-6］。此类方法的主要难点在于精确提取特征点在激光雷达坐标系下的坐标值。不少学者为提升特征点的精确度做了大量研究工作。基于标定板几何特征的方法一般使用黑白棋盘格标定板或自制标定物作为标定设备［7］。livox_camera_lidar_calibration 方法使用棋盘格作为标定物，实现激光雷达和相机外参数的手动校准。文献［8］设计了多边形标定板，根据激光雷达在标定板边缘的扫描点进行直线拟合，点云特征点即为相邻拟合直线的交点。然而，该方法仅适用于分辨率较高的激光雷达。为满足低分辨率激光雷达特征点提取需求，文献［9］提出一种基于Hough变换的关键点提取方法，该方法采用时域多帧融合算法增加点云密度，提取的关键点更为精确。文献［10］以立体纸箱为标定物，提出用平面拟合方法获取相邻纸箱平面相交线，根据纸箱实际尺寸进而确定纸箱角点位置。此类平面拟合方法提取的特征点比边缘直线拟合方法的更为稳定。除此之外，不少学者也尝试利用环境特征的方法确定激光雷达和相机坐标系下对应的特征点。文献［11］基于自然场景中的线性元素，获取点云数据中的 3D线段和图像数据中的 2D 线段作为特征元素，进而构建优化问题求解坐标系之间的转换矩阵。然而，该方法仅适用于具有明显线性元素的场景。路面和小障碍物也被用作标定校准点，文献［12］提出一种自标定算法，该方法仅利用路面的平面特征和路面障碍信息物实现激光雷达与相机的俯仰角、滚转角和偏航角校正。

近年来，深度学习及其他智能算法也被逐渐应用于激光雷达和相机的外参数标定领域。文献［13］基于深度学习方法首次提出RegNet模型，该模型可实现端到端预测激光雷达和相机位姿转换的 6 个自由度参数。文献［14］提出一种自监督网络CalibNet模型，其通过最大化输入图像和点云之间的几何结构和光度一致性训练模型，实现对外参数的准确标定。文献［15］提出一种LCCNet 模型，该模型不仅可以实现数据端对端训练，还能实时在线校正激光雷达和相机的外参数。

综上所述，基于环境特征的标定算法鲁棒性依赖特定自然环境物体特征提取准确度，受环境限制较大；基于深度学习模型必须依赖海量的高精度训练数据，并且针对不同传感器模组需要重新训练模型，同一模型参数不能迁移到不同传感器布置的新场景，泛化性能差且成本较高。为得到高精度且高泛化性能的标定方法，本文提出基于特征匹配的激光雷达和相机标定算法。该算法设计特定标定物，在图像特征点提取时考虑标定板空间投影图像问题，加入椭圆约束，以准确提取二维（2D）椭圆特征；在点云特征点提取时，叠加多帧点云，采用平面拟合方法，实现降维提取三维（3D）球心特征；接着构建点到点代价函数，采用非线性算法优化外参数矩阵，实现兼顾高精度和高泛化性的参数标定。

1 基本原理

1.1 外参数标定原理

外参数标定是求解相机和激光雷达坐标系间变换关系的过程。两个三维坐标系间的变换为刚体运动，可以用旋转矩阵和平移矩阵表示。设P为三维空间内一点，（XL，YL，ZL）为点P在激光雷达坐标系下的坐标值，（XC，YC，ZC）为点P在相机坐标系下的坐标值，则有

式中：R——3×3 矩阵，表示激光雷达坐标系相对于相机坐标系的旋转关系；T——三维向量，表示激光雷达坐标系相对于相机坐标系的平移关系；［R|T］——激光雷达与相机间的外参矩阵；ti——T向量的第i个元素，其中，i=1，2，3；rij——R矩阵第i行第j个元素，其中，j=1，2，3。

相机数据通常以图像的形式表示，物体在图像中的坐标位置以像素为单位。因此，还需要将点P的相机坐标值转换为像素坐标值，这个过程可以用小孔成像模型来描述。根据小孔成像模型，点P的像素坐标值（u，v）可表示为

式中：fx和fy——相机焦距；cx和cy——相机主点坐标；K——相机内参矩阵，为相机传感器自身固有系数，可通过张正友棋盘格法获得。

综上，点P 的像素坐标值和激光雷达坐标系的转换关系为

根据式(5)可知,通过获取不同点在激光雷达坐标系下的坐标值和像素坐标系下的坐标值,可以构建n点透视位姿(perspective-n-point,PnP)问题,并基于非线性优化算法求解激光雷达和相机坐标系间的旋转矩阵R和平移矩阵T。

1.2 基于特征匹配的联合标定方法

标定板图像示意见图1。图中自制矩形标定板的长宽为 80 cm×60 cm，标定板被挖空2 个圆孔。将标定板置于激光雷达和相机的共同视野内，采集相应点云数据和图像数据；选取标定板挖空圆孔圆心作为特征点，提取点云数据特征点的3D 坐标值和图像数据特征点的2D 坐标值；建立对应特征点匹配约束方程组，采用非线性优化算法求解激光雷达和相机的最优外参数矩阵。

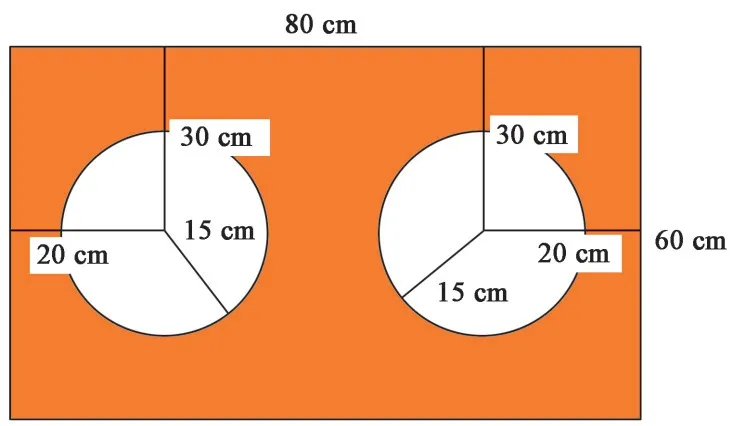
图1 标定板图像示意Fig.1 Schematic diagram of calibration board image

1.2.1 点云数据球心特征提取算法

点云数据球心特征提取算法用于提取标定板圆心在激光雷达坐标系中的点云三维坐标。具体步骤如下：

1）提取标定板平面。激光雷达产生的单帧点云数据稀疏，标定板轮廓不清晰，影响特征点提取的准确性。本文采用多帧点云叠加的方式获取稠密点云数据，并设计自适应直通滤波器，提取标定板平面。为加快点云处理速度，使用体素网格划分的方式［16］对标定板平面进行点云滤波处理，达到降低点云密度的目的。

2）平面拟合去噪。为减少点云数据噪点，对体素滤波后的点云数据进行平面拟合，并计算点云中各点到拟合平面的距离d，如果d≥ 0.01 m，则将该点标记为异常点并删除，重新拟合平面，直到拟合平面中任意点云到平面的距离小于0.01 m。

3）图像增强。为有效提取标定板圆心特征点，将上述三维点云投影至二维图像平面，构成投影图像，由于图像中有点云映射的像素点较少，因此本文采用卷积的方式对图像进行平滑处理，达到增强图像目的。

4）反投影求解三维坐标。以标定板圆孔内任意位置为起始点，通过向外搜索算法寻找圆孔边缘所在的像素坐标，并根据最小二乘法拟合圆，获取图像圆心坐标。基于投影平面和三维平面投影关系，反投影得到标定板圆心在激光雷达坐标系下的三维点云坐标 。图2是激光雷达点云特征点提取效果图，绿色点表示激光雷达点云在标定板上的反射点，绿色球体球心即为点云特征点。

图2 激光雷达点云特征点提取效果Fig.2 Effect of extracted feature points in LiDAR point cloud

1.2.2 图像数据椭圆特征提取算法

图像数据椭圆特征提取算法用于提取标定板圆心在图像像素坐标系下的坐标值。具体步骤如下：

1）自适应图像分割。根据标定板在图像中的像素值，设置二值化阈值将图像转为灰度图。由于光照造成标定板反光且图像中存在与标定板像素值相近的景物，采集图像存在噪点，因此将二值化图像进行腐蚀处理。腐蚀处理后的图像中，最大连通白色区域为标定板所在位置，据此，基于最大稳定极值区域轮廓算法提取标定板。

2）提取图像椭圆圆心。标定板在实际摆放过程中存在倾斜，使得挖空的圆孔在投影图像中往往以椭圆的形式存在。为精准提取圆心位置，首先采用基于局部极值的分水岭算法拟合得到标准圆，接着向外拓展一定距离得到每个圆孔轮廓包裹范围。在包裹区域内，采用 canny 边缘检测算法获取椭圆边缘点并进行椭圆二乘拟合，平面椭圆的一般方程为

其中，（x，y）为椭圆上的点坐标。根据式（6）可求得椭圆方程的5 个参数B、C、D、E、F，标定板圆心在图像像素坐标系下的坐标值（xc，yc）即为

图3 是图像特征点提取效果图，其中绿色圆圈是提取的椭圆曲线，其圆心坐标为相应特征点的像素坐标值。

图3 图像特征点提取效果Fig.3 Effect of extracted feature points in image

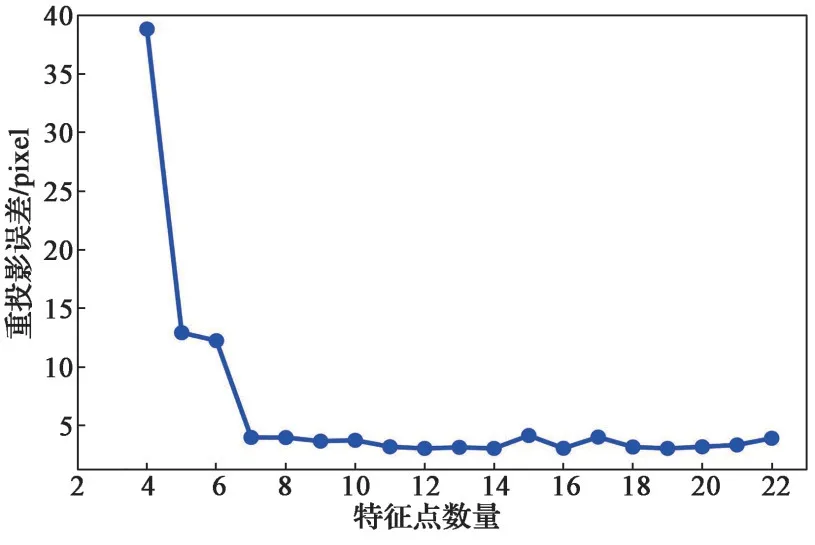
图4 重投影误差随特征点数量变化情况Fig.4 Variation of reprojection errors with different numbers of feature points

图5 点云投影到图像的效果图Fig.5 Effect of point cloud projected onto image

1.2.3 3D-2D 特征匹配与外参数优化算法

利用多个特征点在激光雷达坐标系中的坐标及其在图像中的投影像素坐标，可以解出相机坐标系与激光雷达坐标系之间的绝对位姿关系，包括平移向量T以及旋转矩阵R，求解位姿关系至少需要3 组不同的特征点［17］。

根据点云数据球心特征提取算法和图像数据椭圆特征提取算法，获取标定板圆心特征点在雷达坐标系中的点云三维坐标值和像素坐标系中像素二维坐标值。设定激光雷达和相机之间的外参数矩阵初值，根据式（5）将三维点云投影至二维图像，并以圆心距离为约束条件，建立标定板圆心像素二维特征值与点云三维特征值的匹配关系。以点到点的距离方式建立代价函数，优化外参数矩阵，并将点与点之间距离定义为标定板圆心点云三维坐标与对应像素二维坐标之间的重投影误差。设Ej′表示激光雷达点云圆心PL，j′与二维图像中对应圆心坐标PC，j′之间的重投影误差，则

对获取的n组特征点的重投影误差做最小化处理，构建代价函数：

①判断信息题，提醒自己。信息题的题干所占篇幅往往较大，很好识别。信息题往往是区分度很大的试题，无论是选择题还是判断题，提醒自己慢下来好好作答。②理清信息间的逻辑关系与教材的结合点，必要时通过画图帮助理解。③问答中必有用到信息的地方，有些信息还需要进行转换。

采用 Levenberg-Marquardt（LM）算法对式（9）进行优化，获得精确的外参数矩阵。

2 实验验证与分析

为了测试标定方法的有效性，对标定方法进行了定量分析、定性分析和对比分析实验。实验使用的相机焦距为8 mm，相机像元尺寸为3.75 μm，图像分辨率为1 920×1 080；激光雷达视场角为90°（H）×10.2°（V），角分辨率最高可达 0.1°；算法处理设备为惠普 340G7 笔记本电脑，操作平台为 Ubuntu 18.04 下的机器人操作系统，编程语言为C++。

2.1 定量分析

在激光雷达和相机共同视野范围内摆放标定板，一共取得11 组不同标定板位姿。使用点云数据球心特征提取算法和图像数据椭圆提取算法分别提取标定板圆心的三维点云坐标和二维像素坐标，共获得22 组对应数据。基于重投影误差建立优化函数，并根据LM 非线性优化算法优化激光雷达和相机的外参数矩阵。

基于求解的外参数矩阵，将标定板圆心在激光雷达坐标系下的坐标值投影到图像坐标系上，得到对应投影像素坐标。表1 为实际像素坐标值（u，v）和对应投影像素坐标值（u′，v′）的记录值，eu和ev分别为图像水平u方向和垂直v方向的像素误差。

表1 特征点实际像素坐标值与投影像素坐标值误差Table 1 Error between actual pixel coordinates and projected pixel coordinates of feature points

u方向上的平均误差为

v方向上的平均误差为

式中：（uj′，vj′）——第j'组特征点实际像素坐标值；（，）——第j'组特征点对应投影像素坐标值。

为分析特征点的数量对外参数标定误差的影响，从表1 的22 组数据中任选3 组以上特征点数据进行标定实验。以平均重投影误差em为标准来判定标定精度。平均重投影误差计算方式为

式中：em——第m次实验的平均重投影误差。

平均重投影误差随特征点数量变化如图 4 所示，由图可知，平均重投影误差随着特征点数目的增多而逐渐减小。当特征点数量小于6 时，平均重投影误差较大且随着特征点数量的增多，误差下降幅度较大；当特征点数量大于6 时，平均重投影误差虽存在局部小幅度波动，但总体误差较小且趋于稳定。

为评估算法复杂度，从表1 的22 组数据中任选10 组特征点数据进行标定实验，重复实验5 次，每次实验均使用同样初值迭代计算300 次。表2 为每次实验的平均重投影误差和算法收敛时间，由表2可见，采用本文方法可以在40 ms 内完成迭代计算，且平均重投影误差小于3.5 像素。

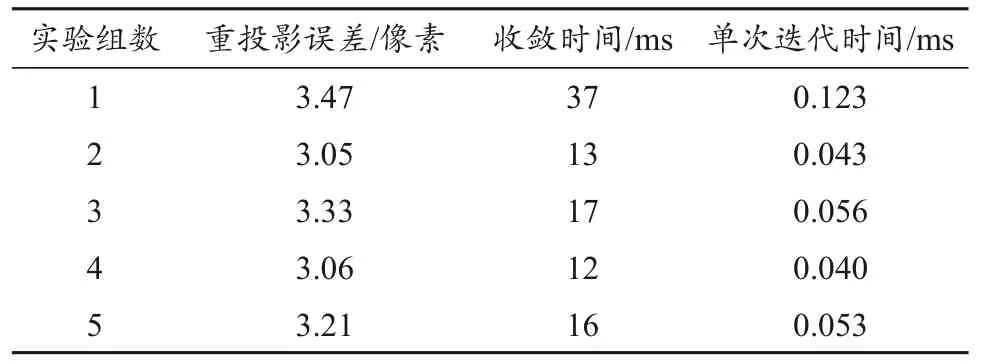
表2 重投影误差和收敛时间数据Table 2 Reprojection errors and convergence times

2.2 定性分析

为了客观地观察标定效果，根据标定所得的外参数矩阵将三维点云投影至二维图像上，并将其可视化。图 5 为空间标定结果，可以看出，图像存在深度差区域，激光雷达边界明显，说明该方法取得了优异的标定效果。

2.3 对比分析

为进一步验证本文方法的优势，使用livox_camera_lidar_calibration 方法和本文方法进行了对比实验。以棋盘格为特征物，采集棋盘格角点在图像和激光雷达的实际坐标位置，共8 组。基于两种方法得到外参数，并将激光雷达实际坐标投影到图像上，得到投影的图像坐标系，然后按照式（12）计算重投影误差。

表3 和表 4 统计了livox_camera_lidar_calibration 方法与本文方法的标定精度，并在表中对误差较小的数值进行了加粗标记。由表3可知，两种方法的平均投影误差分别为2.13 像素和3.75 像素，误差方差分别为1.26像素和2.89像素。与livox_camera_lidar_calibration方法相比，本文的平均标定误差减少了40.8%，误差方差减少了 56.4%，说明该方法的精度与鲁棒性均优于 livox_ camera_lidar_calibration 方法。

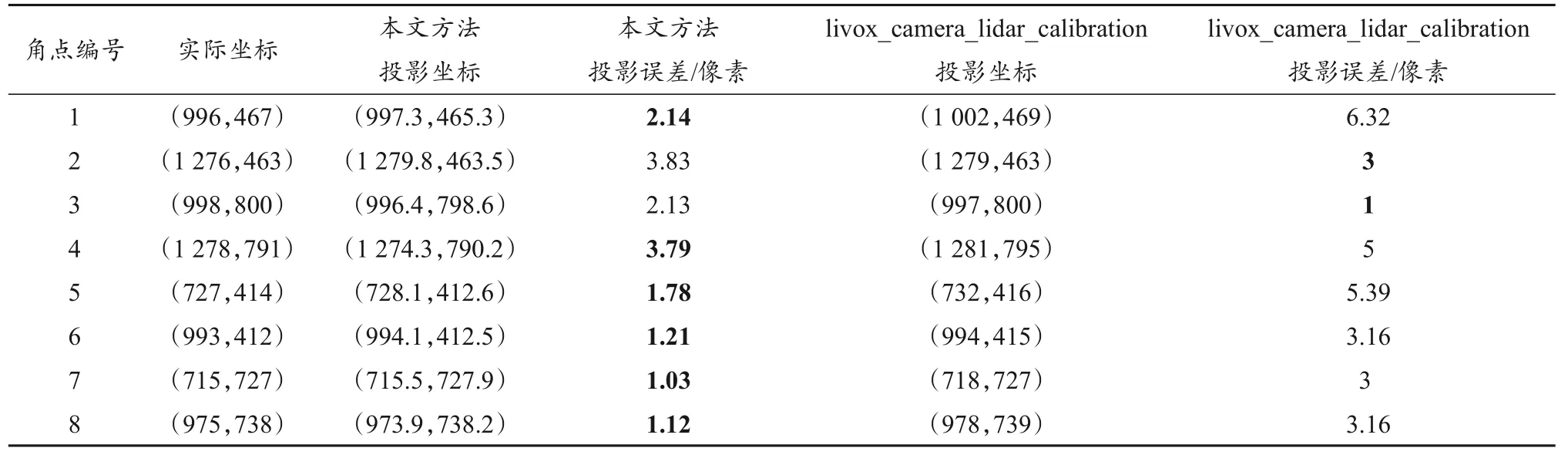
表3 不同方法对比误差分析Table 3 Comparison of errors between different methods

表4 误差统计Table 4 Error statistics

3 结束语

精确稳定的外参数标定是感知系统信息融合的基础。针对激光雷达与相机特征点提取困难且精度低的问题，本文提出了一种基于特征匹配的激光雷达和相机的标定方法。首先，采用降维的方法提取标定板圆心的激光雷达三维点云坐标值，并提出图像数据椭圆特征算法提取特征点的像素坐标值；然后，设置相机和激光雷达初始外参数矩阵，建立对应圆心特征点约束，采用非线性优化算法优化外参数矩阵；最后，利用优化后的外参数矩阵将激光雷达点云投影至图像。验证结果显示，激光雷达点云投影到图像上的平均误差为横向 3.06 像素和纵向 1.19 像素；相比 livox_camera_lidar_calibration方法，本文外参数标定方法的平均投影误差减少了40.8%，方差减少了56.4%，说明该方法能得到精准且稳定的外参数。由于车辆在运行过程产生的振动会使传感器安装位置发生改变，因此基于初始外参数标定需要实时修正，而这将是下一步的研究重点。