基于强化学习的新能源场站储能一次调频自适应控制策略

孙 冉，王建波，马彦钊，张小科，胡怀中

（1国网河南省电力公司，河南 郑州 450000；2西安交通大学自动化科学与工程学院，陕西 西安 710100；3国网河南省电力公司电力科学研究院，河南 郑州 450052）

在推进“双碳”目标达成的背景下，我国电力市场正逐步迈向清洁能源发电为主、传统能源为辅的新型能源结构，预计截止到2060 年我国风电和光伏等新能源发电的年新增装机规模都将保持在较高水平[1]。而新能源发电自身出力的波动、高比例电力电子器件并网和传统机组占比下降都将给系统的频率支撑能力带来不利影响，为电网调频安全带来艰巨的挑战[2-3]。在不同种类的新型调频资源中，电池储能因其具备快速响应和运行稳定等特性，充分契合新型电力系统下的调频需求，已逐渐发展成为电网调频研究中的热点。

在电池储能参与一次调频的控制策略研究中，虚拟下垂控制和虚拟惯性控制为其参与调频时的两种主要控制策略。黄际元等[4]通过分析两种控制模式在时域下的灵敏度曲线得出虚拟惯性控制在扰动前期起主要作用，虚拟下垂控制在扰动后期起主要作用的结论，并据此提出一种前期为虚拟惯性控制，在频率变化率为零时刻切换为虚拟下垂控制的直接切换方法实现储能参与快速调频。该方法减轻了传统电源的调频负担，但会造成储能出力在两种控制策略切换时刻的较大突变，给电网带来二次频率波动，影响储能的长期运行寿命。李军徽等[5]提出了一种基于权重因子的调频控制方法，通过解析函数获取两种控制策略的权重因子，将直接切换法前期的仅虚拟惯性控制优化为虚拟惯性控制向虚拟下垂控制的过渡。李欣然等[6]同样在不同调频阶段设计不同的解析函数来确定储能通过虚拟下垂和虚拟惯性控制参与调频的分配系数来改善储能调频效果。上述两种方法都解决了直接切换法的痛点问题，但其出发点均是基于阶跃扰动下的理想一次调频过程，在实际场景下的适用性仍待考量；此外上述方法中解析函数的参数设置也会影响不同工作环境下储能的调频效果。王育飞等[7]提出一种基于模糊控制的电池储能一次调频自适应综合控制策略，通过模糊控制器获取储能基于两种基本控制策略参与调频的出力系数，其模糊逻辑设计主要基于一次调频理论分析及工程经验，在复杂工况下的适应性较低。吴启帆等[8]提出了正负虚拟惯性的综合控制方法来减小频率曲线的抖动，快速响应频率变化，但该控制策略的执行需要前后经过频差死区和频差变化率死区，关于频差变化率死区的设置未给出具体数值，该死区的设置与虚拟惯性出力时机和大小密切相关，如设置不当，会与虚拟惯性控制策略本身在调频前期能较好抑制频差变化率的优势相悖。

近年来，强化学习因其在复杂系统中的出色控制和决策能力，已在电力行业的不同应用场景中被广泛研究[9-11]。针对现有研究中存在的问题，本工作拟考虑新能源场站出力波动特征，提出一种基于强化学习的新能源场站储能一次调频自适应控制策略。该控制策略中，智能体通过学习在新能源发电出力扰动下使得一次调频效果最优的虚拟惯性和虚拟下垂控制出力占比分配经验，进而通过多回合训练获取储能参与一次调频的出力分配模型。该模型能够根据频率偏差和频率偏差变化率自适应调整虚拟惯性和虚拟下垂两种控制方法参与调频的分配比例，解决当前研究中储能不同控制方法切换策略适应性不足的问题，实现不同调频工况下两者的最优结合，缓解由新能源发电出力变化引起的频率波动。此外本工作方法还将避免储能出力发生突变，减少电池储能瞬时功率需求。

1 含新能源场站的区域电网频率响应模型

为研究基于强化学习的新能源场站储能一次调频自适应控制策略，忽略电力系统电压和功角特性，考虑新能源电站类型为风力发电，建立如图1所示的含储能新能源场站参与一次调频的频率响应模型[12]。图1 主要包含传统调频机组、电池储能系统、风电机组、旋转惯量与负荷四部分模型。图中风电机组不参与一次调频，其输出功率波动∆PW(s)将作为该区域电网的主要功率不平衡扰动；电池储能系统的储能控制器主要根据经过死区环节后的系统频差来调节电池储能参与一次调频的出力指令。图1 中，s为拉普拉斯算子；Kg为传统机组的转速放大倍数；H和D分别为系统惯性和阻尼常数；∆f(s)为系统频差；∆Pg(s)和∆Pb(s)分别为传统机组和电池储能调频出力变化量；∆PW(s)为风电机组出力波动；Gg(s)和Gbess(s)分别为传统调频机组和电池储能系统的传递函数。

图1 含储能新能源电站的区域电网频率响应模型Fig.1 System frequency response model of new energy power station with energy storage

传统调频机组的传递函数Gg(s)主要由调速系统传递函数Ggov(s)和汽轮机系统传递函数Ggen(s)两部分构成，具体表达式如下[13]：

式(1)中，Tg为转速变换时间常数；式(2)中，FHP为高压缸比例系数，TRH为再热时间常数，TCH为蒸汽容积时间常数。

电池储能系统中，Er为电池储能的容量，SOC(state of charge)为储能的荷电状态，SOC0为电池储能的初始荷电状态。储能对象的传递函数Gbess(s)具体表达式如下[14]：

式中，Tbess为电池储能功率转换时间常数。

风电机组模型如图2所示，图中ωr为实际转子转速；ωref为转速参考值；β为桨距角；Ht为风机的惯性时间常数；Tm和Te为机械转矩和电磁转矩。有关图2中风轮模型的具体表达式、桨距角控制系统和最大功率跟踪控制的原理详见文献[15-16]。

图2 风电机组的有功控制模型Fig.2 Active power control model of wind turbine

目前，电池储能参与一次调频的两种基本控制策略为虚拟惯性控制和虚拟下垂控制，根据系统频差并通过上述两种控制策略获得储能一次调频出力指令的表达式如式(4)和式(5)所示：

式(4)和式(5)中，∆Pd(s)表示储能通过虚拟惯性控制得到的调频出力；∆Pp(s)表示储能通过虚拟下垂控制得到的调频出力；Mb和Kb为电池储能的虚拟惯性出力系数和虚拟下垂出力系数。在新能源功率阶跃扰动下，由于虚拟惯性出力与频差变化率成比例关系，通常在扰动初期，系统频差变化率大，储能通过虚拟惯性控制可以快速出力，阻碍频差变化率变化，但对系统稳态频差不起作用，且在频差变化率方向与频差方向不一致时会抑制频率恢复[17]。虚拟下垂出力与系统频差成比例，在频率调节时有一定延迟，主要调节系统频率的稳态偏差[18]。考虑到当前电池储能调频时的两种控制策略在一次调频不同时期起到的作用不同，若能将两者在调频过程中适当结合，使得其优势互补，则能更好地抑制新能源出力波动带来的频率扰动，进一步发挥储能快速调频的优势，减小网侧调频压力。现有将两种控制策略简单结合或叠加的方法存在电池储能出力易发生突变、部分时刻抑制频率恢复和适用调频场景有限等缺点，因此考虑针对新能源场站储能的实际应用场景设计一种利用强化学习算法来获取虚拟惯性和虚拟下垂出力在调频过程中自适应分配方法的电池储能参与一次调频的控制策略。

2 基于强化学习的新能源场站储能参与一次调频的自适应控制策略

2.1 算法整体框架

为实现电池储能参与调频时虚拟惯性出力和虚拟下垂出力的最优分配，提出的自适应分配方法原理如式(6)～(8)所示。

式(6)和式(7)中，∆Pbd(s)和∆Pbp(s)分别为最优分配后的虚拟惯性出力和虚拟下垂出力调频指令；a1和a2分别为所提最优分配方法获取的虚拟惯性分配系数和虚拟下垂分配系数，满足下式关系：

由式(8)可知，储能在参与一次调频时的总出力由虚拟惯性出力和虚拟下垂出力组成，两者在不同调频时期的权重由a1和a2来自适应调节，a1和a2的具体数值由训练得到的智能体获得。根据式(8)设计如图3所示的储能控制器，图中，k1和k2分别为频差和频差变化率的缩放系数。电池储能在参与一次调频时，系统频差经死区环节后进入储能控制器，此时频差和频差变化率经比例环节后通过智能体获得虚拟惯性分配系数，同时计算出虚拟下垂分配系数；然后根据分配系数与对应频差和频差变化率计算虚拟惯性和虚拟下垂出力，最后将两种控制策略的出力相加得到储能调频时的最终调频出力指令。

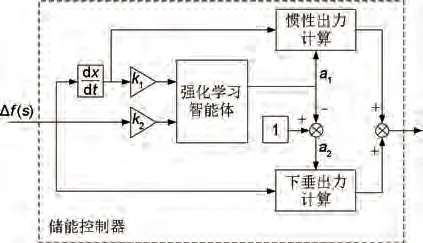
图3 储能参与一次调频的自适应控制器Fig.3 Adaptive controller with battery storage in primary frequency regulation

2.2 新能源场站出力扰动

本工作拟通过强化学习算法在新能源场站出力扰动下训练智能体以实现对储能出力方式的最优分配。根据所搭建的区域电网频率响应模型，强化学习智能体需要在新能源场站出力扰动下根据历史经验不断学习来更新智能体参数，新能源场站的出力主要由风速输入图2所示风电机组模型获取。目前常用于拟合风速的分布模型主要为威布尔分布，其概率分布为

式中，c为尺寸参数，k为形状参数[19]。由文献[19]知，不同新能源场站的风速分布模型具有较大差异，因此不同新能源场站出力特征具有明显差异，本工作考虑针对某特定新能源场站，获取其出力扰动作为智能体训练输入。威布尔分布的参数可以通过最小二乘法获取，将风速按不同区间进行概率统计可得其频次f1，f2…fn，以及p1=f1，p2=p1+f2，…，pn=pn-1+fn，对应参数的计算公式如式(11)～(14)所示。

式中，vi为第i个风速样本，n为非零的风速数据个数。

为了给智能体施加具有新能源场站历史出力特征的扰动进行训练，首先需要收集大量新能源场站或地区历史风速数据，并根据式(11)～(14)计算风速概率统计分布参数，获取该地风速统计分布规律。然后根据风速概率分布生成随机序列，最后根据图2所示风电机组模型即可获得新能源场站出力波动数据。

2.3 基于DDPG 算法的虚拟惯性和虚拟下垂出力自适应分配模型

深度确定性策略梯度（deep deterministic policy gradient，DDPG）算法是一种适用于解决连续控制问题的强化学习算法，其主要框架为Actor-Critic（策略-价值）网络，是对传统DQN（deep Q-network）算法基本思想的扩展，有关DDPG算法的详细原理可参考文献[20]。

本工作采用DDPG算法求解电池储能参与一次调频时虚拟惯性和虚拟下垂出力的自适应分配模型，基于新能源电站出力波动数据，利用智能体在所搭建的含储能新能源电站的系统频率响应模型中交互学习，根据获取的经验不断训练智能体，使得储能在调频时能够自适应分配两种出力方式的权重，满足调频效果和出力最优。DDPG算法中的关键变量设计如下。

（1）状态s

一次调频过程中，系统频差和频差变化率在不同一次调频阶段的特征明显不同[4]，可以用两者来区分当前时刻位于一次调频总过程的不同时期。此外，考虑到储能虚拟惯性出力和虚拟下垂出力大小与系统频差和频率变化率直接相关，因此将状态变量定义为经过电池储能死区环节后的系统频差和频差变化率。

（2）动作a

智能体的动作定义为电池储能参与一次调频时的虚拟惯性分配系数，满足a∈[0,1]。根据智能体的动作以及虚拟惯性分配系数和虚拟下垂分配系数的关系可以计算出虚拟下垂分配系数的具体数值。

（3）奖励函数r

奖励函数的设计如式(15)所示。奖励函数r主要包括r1和r2两部分，式中α和β为两部分奖励的比例系数，∆f为系统频差，∆Pb为电池储能出力变化量。奖励r1用来衡量智能体动作对储能参与调频效果的优劣，奖励r2则避免储能出力过大影响长期调频能力以及自身使用寿命。

此外，在智能体训练过程中还需满足以下约束条件：

式(16)中，∆Pb,t为储能在t个控制间隔时的出力变化量；∆Pb,min、∆Pb,max分别为储能某一控制间隔出力变化量的上、下限；式(17)中，∆Pr,min、∆Pr,max分别为储能相邻控制间隔出力变化量的上、下限；式(18)中，∆fmin、∆fmax分别为系统频差的上、下限。

本工作所提出的基于DDPG算法的虚拟惯性和虚拟下垂出力自适应分配模型的整体框架如图4所示。在图4中，DDPG算法整体包含4个神经网络：策略网络及其目标(Target)策略网络、价值网络及目标(Target)价值网络。其中Q(s,a|θQ)表示价值网络的评价函数，μ'(s'|θμ')表示Target策略网络的策略函数；θT表示目标网络的网络参数；θ表示策略或价值网络的网络参数，τ为目标网络更新参数。智能体训练的环境为第一部分搭建的含储能新能源电站的区域电网频率响应模型。

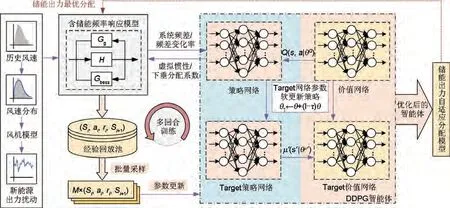
图4 基于DDPG算法的虚拟惯性和虚拟下垂出力自适应分配模型的整体框架Fig.4 The framework of virtual inertia and virtual sag adaptive distribution model based on DDPG algorithm

在每一训练回合开始前，首先根据地区风速概率分布生成一段随机风速扰动，然后通过风电机组模型生成连续功率扰动来模拟仿真环境训练时的调频场景。假设在该回合的第t个时刻系统的状态st=[∆ft,d(∆f)/dt|t]，通过策略网络可以获得此时动作at即储能的虚拟惯性分配系数为：

其中，μ(st)为策略网络输出；N为策略网络输出噪声，可用来增加智能体探索程度。储能在仿真环境中执行动作at后可以得到当前时刻的奖励rt和下一时刻的状态st+1。DDPG算法在训练时通过经验回放技术将智能体与环境交互产生的(st,at,rt,st+1)序列储存在经验回放池中，每次迭代时通过批量采样的方法从中随机抽取M组历史数据对策略网络和价值网络参数进行更新，并在每回合对目标网络的参数通过软更新的方法进行更新。

智能体的整体训练流程为：

步骤1：初始化策略和价值网络及其目标网络的参数，设置训练时的学习率、软更新参数和经验回放池大小等；

步骤2：根据风速概率分布生成随机风速，通过风电机组模型获取该回合用于训练智能体的连续扰动；

步骤3：智能体根据该扰动下的初始频差和频差变化率获取动作，储能执行出力分配指令，根据仿真环境获取当前时刻的奖励以及下一个时刻的系统频差及其变化率；

步骤4：将包含当前时刻状态、动作、奖励和下一时刻状态的经验序列储存在经验回放池中，并从其中抽取一定数量样本对网络参数进行更新，直至达到回合最大步数结束本回合训练过程；

步骤5：重复上述步骤至最大训练回合数。

经过多个回合的训练后智能体在每回合获得的奖励之和趋近于收敛，此时智能体能够在储能参与调频过程中实时根据系统频差和频差变化率对储能的两种控制策略出力权重进行最优分配，如图3所示，智能体负责在储能参与一次调频的自适应控制器中输出储能参与一次调频时的虚拟惯性分配系数，然后根据式(6)～(9)获取储能参与一次调频的总出力指令。优化后的储能出力将提高频率稳定效果，进一步发挥储能参与调频的潜力。

3 算例仿真

3.1 智能体参数及训练过程

本工作中DDPG算法的策略网络包含3个隐藏层，神经元个数分别为50、25、25；价值网络包含2个隐藏层，神经元个数分别为50、25。其他训练相关参数设置如表1所示。此外，智能体训练以及后续仿真验证部分所使用的区域电网频率响应模型选取了某区域电网作为仿真对象。该区域电网主要由传统调频机组和一个新能源场站构成，其中传统调频机组的额定容量为100 MW，新能源场站包含十台容量为1.5 MW 的风电机组。该区域电网负荷容量约为60 MW，传统调频机组工作在50%负荷，新能源平均出力约为10 MW。考虑为新能源场站配备单独的储能装置用于参与一次调频服务，电池储能的容量为2 MW/2 MWh，初始荷电状态为0.5。传统调频机组和储能的一次调频死区均设置为±0.033 Hz，其余模型参数如表2 所示，所有模型参数在训练及仿真时都将以额定数值为基准进行标幺化。

表1 DDPG算法参数设置Table 1 DDPG algorithm parameter settings

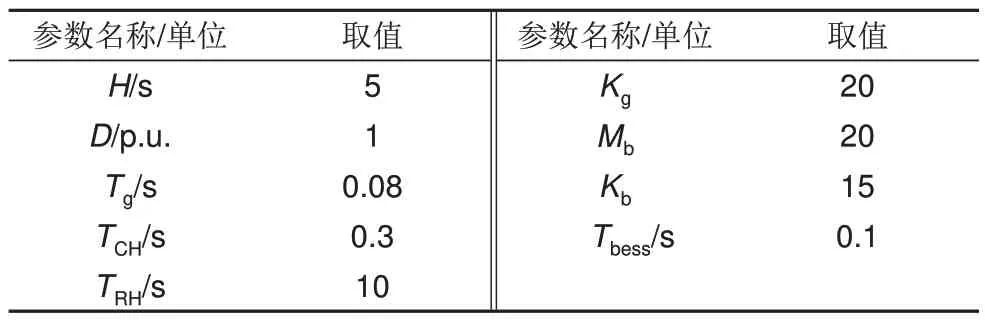
表2 区域电网频率响应模型仿真参数Table 2 Regional power grid frequency response model simulation parameters

智能体训练的具体硬件环境为11th Gen lntel(R) Core(TM) i5-11400 @ 2.60 GHz CPU、32 GB内存的计算机，DDPG算法代码编写以及训练均通过Matlab/Simulink 平台完成，获取最终智能体的训练过程中奖励函数值的变化曲线如图5所示。

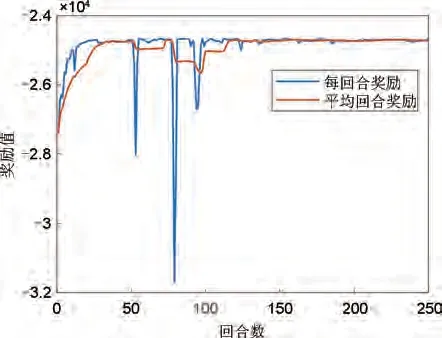
图5 强化学习训练过程Fig.5 Reinforcement learning training process

图5中蓝色曲线为训练过程中每回合奖励值变化趋势，橙色曲线为每20 个回合的平均回合奖励值变化趋势。由图5可以看出，训练前期智能体由于处在学习阶段，其奖励值由初始奖励值不断快速上升，在训练中期由于与环境的不断探索与训练过程中动作的随机性使得回合奖励值出现较大波动，但在训练后期回合奖励和平均回合奖励值不断趋于收敛，说明此时智能体已经通过不断训练与学习，能够在实际调频场景中进行储能调频出力方式的最优决策，使得回合奖励值最大。

3.2 一次调频评价指标

为验证本工作所提基于强化学习的新能源场站储能一次调频自适应控制策略的有效性，本工作将通过新能源发电突变和新能源发电连续波动两种扰动形式对不同控制策略进行仿真对比。在新能源发电突变扰动下，使用最大频率偏差∆fmax、最大频率偏差变化量绝对值|∆omax|和稳态频率偏差∆fs作为调频效果的评价指标，单位分别为Hz、Hz/s 和Hz。三个评价指标的值越小，说明调频效果越好。

在连续出力波动下使用fRMSE和td作为调频效果的评价指标，分别代表各采样时刻频率偏差的均方根值之和以及系统频率超出死区边界时间占总仿真时长的百分比，其计算方法如式(20)和式(21)所示。

式(20)中，fi为第i个采样时刻的频率；fn为额定频率，取50 Hz；S为总采样点数目。针对某一连续负荷扰动，fRMSE的值越小，说明电网频率波动越小，储能调频效果越好。式(21)中，Ts为总仿真时长，Td为系统频率超出死区边界的时间，td的值越小，说明系统频率在死区范围内的时长越长，系统频率质量越好。

3.3 新能源发电突变仿真

设在5 s 时新能源场站出现幅值为0.02 p.u.的功率突减，对应的新能源出力曲线如图6所示，将该功率扰动作为∆PW(s)施加在区域电网频率响应模型中。区域电网中传统调频机组和储能共同参与一次调频，两者出力经旋转惯量与负荷环节后获得系统频率的波动结果。对无储能、本工作、文献[6]所提虚拟惯性出力和虚拟下垂出力的切换方法(对比方法)和文献[4]所提直接切换法四种场景进行仿真对比，其中直接切换法为虚拟惯性出力和虚拟下垂出力结合的典型控制方法，而对比方法为在直接切换法基础上的优化方法；直接切换法会导致储能出力突变，对比方法的解析函数设置会影响其实际调频效果，通过上述三种方法对比可以说明本工作方法的有效性。此外，无储能下的仿真结果用来说明当前扰动下仅传统机组参与调频时该区域电网频率的波动情况。仿真得到频率偏差波动曲线如图7所示；不同方法的虚拟惯性分配系数变化如图8所示，其中本工作方法对应智能体的动作，对比方法和直接切换法对应一次调频过程中虚拟惯性控制方式的出力占比；不同方法下的储能出力曲线如图9所示，由虚拟惯性和虚拟下垂出力乘以各自占比后求和获取；不同方法的调频评价指标见表3。

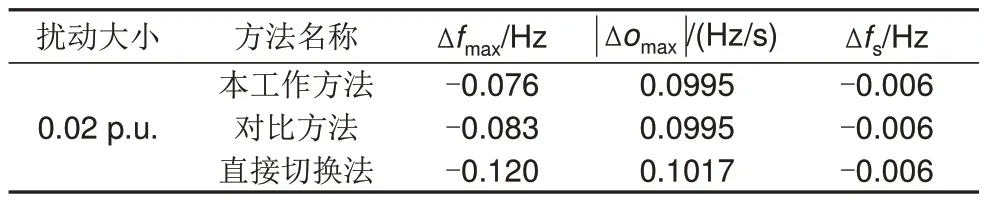
表3 区域电网频率响应模型仿真参数Table 3 Frequency regulation index under sudden change of new energy power output

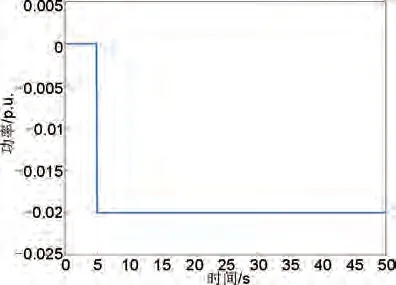
图6 新能源场站出力突变曲线Fig.6 New energy plant output abrupt curve

图7 新能源发电突变下的频差曲线Fig.7 Frequency difference curve under sudden change of new energy power output

图8 新能源发电突变下的虚拟惯性分配系数Fig.8 Virtual inertia distribution coefficient curve under sudden change of new energy power output

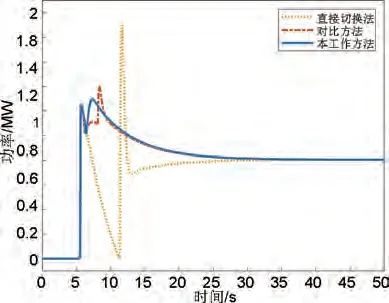
图9 新能源发电突变下的储能出力曲线Fig.9 Energy storage output curve under sudden change of new energy power output

由图7可知，在0.02 p.u.新能源功率突减工况下，三种方法在扰动发生初期频差跌落趋势相同，无储能下频差跌落程度最深，对比方法的频差最低值低于本工作方法，且前两者频差最低值明显高于直接切换法。随后本工作方法缓慢恢复至稳态频率附近，对比方法与直接切换法先有一段快速恢复阶段，随后缓慢变化至稳态频率，直接切换法在恢复阶段有明显超调。由图8可得，直接切换法在固定时刻实现从仅惯性出力到仅下垂出力的切换，对比方法设计了若干过渡时段来实现惯性出力到下垂出力的切换，而本工作方法在前期仅为惯性出力，随后较快将惯性出力的比例下调至零，实现两种控制方式的过渡，保证惯性出力仅调频初期起作用，避免在调频恢复阶段阻碍频率恢复。在图9中，直接切换方法下储能由于在频差变化率为零时实现两种控制方式的切换，故储能出力先降为零后迅速上升。对比方法和本工作方法的储能出力曲线相近，但本工作方法过渡期更短，功率峰值也更低，说明本工作方法可以减小储能的功率需求。目前各省市发布的“并网双细则”中要求，风电场一次调频有功功率滞后时间不大于2 秒、上升时间应不大于9 秒。根据图9 可知，本工作方法中储能作为风电场主要调频电源，其滞后时间和上升时间较快，能够满足相关要求。此外，储能出力超过风电场一次调频功率变化最低限幅，即风电场运行功率的6%，满足风电场一次调频功率变化幅度要求。且风电机组不参与一次调频，可以避免因参与一次调频动作导致风电机组脱网或停机现象发生。在表3中，本工作方法的∆fmax评价指标最优，较对比方法和直接切换法分别减少约8.43%和36.7%；|∆omax|指标与对比方法相同，均优于直接切换法；三种方法的∆fs保持一致。以上说明了本工作方法在新能源发电突变扰动下的表现优于对比方法和直接切换法。

3.4 新能源发电连续波动仿真

新能源发电的连续扰动仿真设置两组不同扰动工况，工况一为图10(a)所示的300 s风速波动产生的新能源电站出力波动，实际新能源出力波动如图10(b)所示，将该功率扰动作为∆PW(s)施加在区域电网频率响应模型中。同样对无储能、本工作方法、对比方法和直接切换法四种场景进行仿真，得到频率偏差曲线如图11 所示，储能输出功率曲线如图12所示，对应调频指标见表4。

表4 工况一的调频指标Table 4 Frequency regulation index of condition one

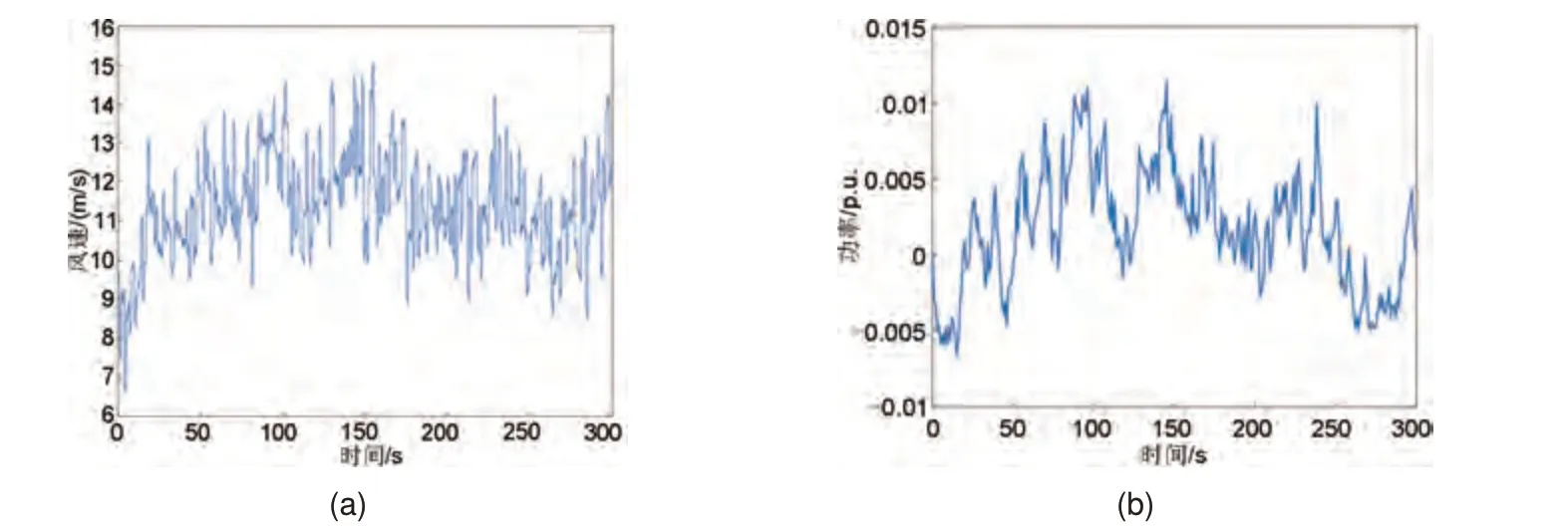
图10 工况一风速和功率波动曲线：(a)风速曲线；(b)功率曲线Fig.10 Condition one wind speed and power fluctuation curve: (a) wind speed curve; (b) power curve

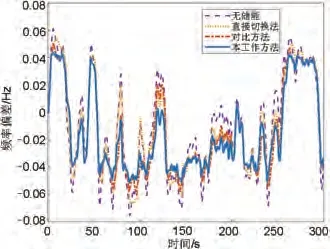
图11 工况一下的频差曲线Fig.11 Frequency difference curve of condition one

图12 工况一不同方法储能的输出功率：(a)0～300 s；(b)212～222 sFig.12 The output power of different methods for energy storage: (a)0—300 s; (b)212—222 s

如图11所示，在工况一的新能源出力波动下，四种场景的频率偏差曲线都出现了较大的振荡，其中无储能情况下的频率波动情况最剧烈。同直接切换法和对比方法相比，本工作方法的系统频差曲线在大部分时间段内明显更贴近频差为零的基准线。此外，相较于本工作方法，直接切换法和对比方法在部分频差转折点的频差会出现较大起伏，因此其表现不如本工作方法。图12 为不同方法下储能的输出功率曲线，其中直接切换法的输出功率波动幅度最大，对比方法和本工作方法的输出功率曲线相近，但对比方法在部分时刻的小幅功率波动频次仍高于本工作方法。由表4 可以得出与图11同样的结论，本工作方法的fRMSE较对比方法和直接切换法分别减少约8.74%和13.83%，td较对比方法和直接切换法分别减少约3.9%和6.7%，两项调频评价指标均为最优，说明本工作方法能在新能源出力大幅波动下减小系统频率波动，优化频率质量，改善一次调频效果。

直接切换法、对比方法和本工作方法中储能的SOC计算方法如图1所示，在工况一的新能源波动下三者的SOC 变化曲线如图13 所示。在该工况下，三种方法的SOC 均有不同程度的降低，其中本工作方法和对比方法下降趋势更为接近。三种方法中本工作方法的SOC 偏移程度最大，说明本工作方法较其他两种方法的一次调频动作量更多，在弥补一次调频过程中的电网功率缺额时起到了更积极的作用，减小了系统频率偏差。结合表4 可知，在该工况下本工作方法的调频评价指标fRMSE更优，频率稳定效果更好。

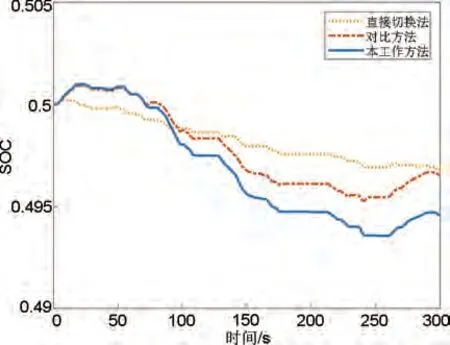
图13 工况一不同方法储能的SOCFig.13 The SOC of different methods for energy storage under condition one

工况二设置为实际新能源出力扰动，图14 为某风电场测量得到的300 s 出力波动，将该功率扰动作为∆PW(s)施加在区域电网频率响应模型中。同样对无储能、本工作方法、对比方法和直接切换法四种场景进行仿真，得到频率偏差曲线如图15所示，储能输出功率和SOC曲线分别如图16和17所示，对应调频指标见表5。

表5 工况二的调频指标Table 5 Frequency regulation index of condition two

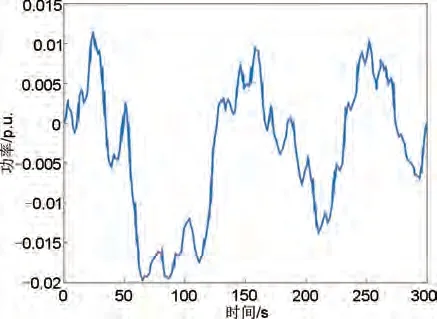
图14 工况二新能源出力波动Fig.14 New energy output fluctuation under condition two

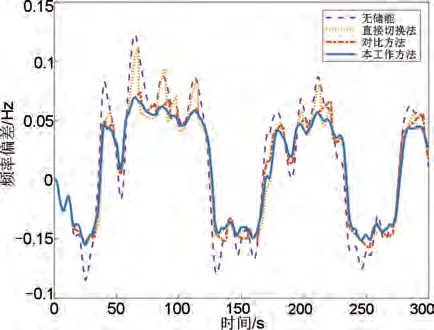
图15 工况二下的频差曲线Fig.15 Frequency difference curve of condition two

图16 工况二不同方法储能的输出功率：(a)0～300 s；(b)36～50 sFig.16 The output power of different methods for energy storage: (a)0—300 s; (b)36—50 s

如图15 所示，三种方法中本工作方法的频差曲线较其他两种方法的频差曲线偏移更小。对比方法在大部分情况下同本工作方法一致，但在频差曲线的拐点附近仍会出现小幅的频率偏移。直接切换法由于依赖频差变化率作为控制方式出力切换时机，因此在大部分频差拐点附近均会出现较大的频差偏移。在图16(a)中，本工作方法和对比方法的储能动作深度在多数时刻明显小于直接切换法，直接切换法较前两者出现了更多的输出功率振荡和出力突变，不利于储能的长期使用寿命；在图16(b)中，对比方法在控制模式临界切换点附近仍会导致部分时刻的小幅出力振荡。在图17 中，三种方法的SOC 在工况二下均有不同程度的上升，其中本工作方法和对比方法变化趋势更为接近。三种方法中本工作方法的SOC 偏移程度最大，说明本工作方法较其他两种方法的一次调频动作量更多。结合表5可知，本工作方法在频差和频率质量两个评价指标上均表现最优，其中本工作方法的fRMSE较对比方法和直接切换法分别减少约11.14%和17.61%，td较对比方法和直接切换法分别减少约1.55%和2.35%，说明本工作方法也能够在实际新能源出力波动下较好地完成一次调频任务，减小系统频率波动，提高频率质量。

图17 工况二不同方法储能的SOCFig.17 The SOC of different methods for energy storage under condition two

4 结 论

本工作针对储能传统虚拟惯性和虚拟下垂控制策略的缺点，考虑新能源出力特征，提出了基于强化学习的储能一次调频自适应控制策略。该控制策略能够根据系统频差和频差变化率自适应调整两种传统控制策略的出力占比，在调频前期通过虚拟惯性控制抑制频差快速变化，在调频中后期通过虚拟下垂控制减小稳态频差。与所设置的三种对比方法相比，所提控制策略在新能源发电突变工况下最少能减小8.43%的最大频率偏差，在新能源发电连续波动工况下最少能减少8.74%的频率偏差均方根，且能在一定程度上减少系统频率波动至调频死区外的时间。以上说明所提方法在不同工况下的频率稳定效果和频率质量维持较好，能够提高新能源场站储能的一次调频能力，对新能源友好并网和维护电网频率稳定有重要意义。