基于多模型神经网络的湿度廓线反演研究

王金虎 肖安虹 陈后财 王昊亮 刘萱 蔡海强

（1.南京信息工程大学 气象灾害预报预警与评估协同创新中心, 南京 210044；2.中国气象局 气溶胶与云降水重点开放实验室, 南京 210044；3.中国科学院 中层大气和全球环境探测重点实验室, 北京 100029；4.南京信大安全应急管理研究院, 南京 210044；5.中国电波传播研究所, 青岛 266107）

0 引 言

准确预报灾害性天气对减少和避免气象灾害的损失具有重要意义，但由于探测手段有限，人们对中小尺度天气的发生机理和规律还不够了解[1-2]，特别是在大气廓线的探测方面，往往采用费时费力的人工释放探空气球的方式，而地基遥感探测仪器(如地基微波辐射计)在大气廓线的探测具有无人值守、时间连续及高精确性的优点，已经成为遥感大气温度、湿度、云液态水廓线的有力工具[3-6]。

地基微波辐射计在反演温度、相对湿度、水汽密度以及液态水含量时主要依赖于亮温的测量。而亮温的测量值除了受设备硬性条件影响外，还受到云、降水等复杂天气现象的影响，同时探空气球可能因漂移而产生测量误差。因此许多学者通过对亮温测量值进行预处理来提升反演精度。如马丽娜等[7]提出利用多通道亮温差值阈值法对亮温进行线性订正；张雪芬等[8]引入测云仪对微波辐射计的亮温进行预处理后改进了反演；鲍艳松等[9]通过MONORTM下行辐射传输模式，利用本地探空资料模拟出亮温数据，对实测亮温进行修正；杨杰波等[10]利用MPM93模型结合辐射传输方程计算的通道模拟亮温完成了对实测亮温结果的订正。上述文献对亮温预处理的反演结果相较于未处理数据均提升了反演的精度。目前，利用亮温反演大气廓线主要采用神经网络算法，相较于之前的正向模型反演算法和回归法，神经网络具有运算时间快及良好的非线性拟合能力，且不需要单独设计复杂的反演算法和模型，因此会减少在分析物理正向模型时产生的众多问题[11-12]，相关学者已验证了神经网络算法在反演大气温湿廓线的优势[13-16]。然而，地基微波辐射计仅能获得亮温数据，对云的探测能力却十分有限[13,17]，导致云的存在对大气廓线尤其是对相对湿度廓线会产生非常大的影响，而温湿廓线的精度会直接影响到水汽密度与液态水含量的计算，因此，有学者尝试在构建的神经网络模型中加入对应的云底高度及厚度或者添加雷达反射率因子以提高反演精度[18-19]，但在不同神经网络模型的反演效果的对比上却尚未进行尝试。

因此，本文构建了3种不同云信息的神经网络模型，并将模型反演结果进行对比，探究提升地基微波辐射计反演湿度廓线精度的神经网络模型。

1 实验介绍及数据处理

1.1 实验介绍

探空数据、毫米波雷达数据以及微波辐射计数据均由ARM大气观测网站提供，测量仪器均位于阿拉斯加北坡（71.32°N, 156.62°W）。其中探空数据为DigiCORA-III型数字探空仪所得，探测高度可达20 km。毫米波测云雷达为Ka波段多普勒天气雷达，测量最大高度为12 km，垂直分辨率为45 m，有10种时间分辨率，最大发射功率为100 W。微波辐射计位于同一地点，输出为47个高度层，0~1 km高度分辨率为100 m，1~10 km高度分辨率为250 m，主要技术参数如表1所示。

表1 微波辐射计主要技术参数Tab.1 Main parameters of microwave radiometer

1.2 数据处理

样本数据时间为阿拉斯加北坡2004-04-19—2006-12-31，测试数据时间为2008-01-10—2008-02-29。样本数据累计589组毫米波测云雷达反射率因子、1 295条探空廓线，以及对应的微波辐射计数据；测试数据累计51组毫米波测云雷达反射率因子，101条探空廓线。为确保数据的可靠性，须提前对样本进行筛选。

1)有云存在，探空数据相对湿度应为100%，但由于凝结核的影响，往往低于100%[17]。因此在探空廓线上，以相对湿度85%为阈值[18]，进行以下划分：将近地面至任意高度层相对湿度均小于85%的划分为晴天；相对湿度于近地面处小于85%，高度超过600 m存在相对湿度大于85%的划分为云天；相对湿度从近地面到600 m都大于85%的划分为雨天。

2)降水会对毫米波云雷达造成严重的衰减，根据黄兴友等[20]对毫米波云雷达回波强度给出的分级，选取反射率因子不超过15 dBZ的样本作为云雷达数据。

3)雨天情况下天线罩上的雨水会使得亮温探测出现异常，所以必须剔除掉1)和2)判定为雨天的亮温集，作为微波辐射计数据。

完成上述3个步骤的筛选后，须对数据进行匹配。如图1(a)和(b)所示2005-07-23T15:02时的探空相对湿度和雷达反射率因子，有云时所挑选出的样本必须保证云雷达与探空数据云底位置及云的厚度基本相同；如图1(c)和(d)所示2006-03-28T 20:53时的探空相对湿度和雷达反射率因子，无云时，测云雷达无明显突变。筛选样本时发现，无论云是否存在，毫米波测云雷达的反射率因子都会逐渐变大，因为该毫米波测云雷达技术参数在不同高度层将会接收到不同最小探测雷达反射率因子，且随着高度升高所能接收的最小探测雷达反射率因子逐渐增大，导致样本数据中很难寻找到高云样本。为增强无云与有云信号之间的对比，无云时对雷达反射率因子大小统一修改为第一个高度层所能探测的最小探测雷达反射率因(-62 dBZ)；有云时，将非云高度层上对应雷达反射率因子大小统一修改为上述值(-62 dBZ)，最后完成微波辐射计与云雷达在时间分辨率上的匹配。由于毫米波测云雷达仪器探测到的中高云较少、混合云数量极少，因此本研究只考虑单层云的情况。用于建模的样本数据共155组，其中晴天样本85条，有云样本70条(低云60条，中云9条，高云1条)；测试样本15条，其中晴天样本9条，有云样本6条，且全部为低云样本。因此，本文将数据集分为有云和无云两种情况。

图1 不同时刻的探空相对湿度和雷达反射率因子Fig.1 Sounding relative humidity and radar reflectivity factor at different times

2 反演模型

理论上神经网络算法可以逼近任意复杂的非线性关系，不需要专门设计复杂的反演算法[12]。如图2所示，采用3层前馈反向传播神经网络(back propagation neural network, BPNN)，其中X为输入层，Y为输出层，中间为隐含层。输入层到隐含层选取双曲正切S型传递函数tansig，隐含层到输出层选取线性传递函数purelin，采用贝叶斯正则化trainbr函数作为学习函数。

建立如下3种不同的反演模型来探究添加不同云信息对BPNN反演模型的影响：

1)将不添加任何云信息的BPNN模型定义为BPNN0，其中输入层节点15个，分别为微波辐射计提供的12个通道亮温及地面的温湿压；输出层节点为47个，为地面到10 km高度的47个不同高度层上的相对湿度。

2) 将添加入云和出云高度的BPNN模型定义为C-BPNN，其中输入层节点17个，前15个节点分别为微波辐射计提供的12个通道亮温及地面的温湿压，后2个节点为入云和出云高度，入云和出云判定方式参照文献[21]；输出层节点为47个。

3) 将添加雷达反射率因子的BPNN模型定义为Z-BPNN，文献[22]对温度廓线反演的研究中发现，不同的分层对反演结果有一定的影响，同时考虑到毫米波测云雷达的库长及BPNN的收敛性，本文以4个库长即180 m对10 km进行划分，加上微波辐射计提供的12个信道亮温及地面温湿压共计70个作为输入层节点，输出层节点为47个。

神经网络性能的好坏易受其隐含层结点数的影响，隐含结点数太少会导致信息不足，影响整个网络的反演精度；而隐含节点数过多会导致训练时间过长，影响工作效率。中间隐含层节点数N为[23]

式中，NX、NY分别输入层和输出层节点数。

3 反演结果

以探空资料为标准，用平均绝对误差(mean absolute error, MAE)及均方根误差(root mean square error, RMSE)检验反演精度：

式中：n为高度层数，取值47；Ui为真实探空廓线；Vi为反演得到的探空廓线。

利用BPNN0、C-BPNN和Z-BPNN 3种BPNN模型对15条测试样本进行反演，结果如图3所示。可以看出：BPNN0反演模型的相对湿度廓线误差波动较大，在2008-01-29T04:42出现最大MAE(38.641 7%)以及RMSE(46.192 6%)；C-BPNN模型MAE为15.945 9%，RMSE为18.419 1%，相较于BPNN0模型MAE减小了22.695 8%，RMSE减小了27.773 5%；而Z-BPNN模型的MAE为21.385 8%，RMSE为25.078 2%，MAE减少17.255 9%，RMSE减少21.114 4%。而误差减少最小的样本为2008-02-29T05:25，BPNN0模型的MAE为11.213 6%，RMSE为16.007 8%；C-BPNN与Z-BPNN模型MAE值分别为11.582 1%，13.066 8%，RMSE分别为16.007 8%，16.171 9%，误差变化范围不大，仅一条样本(2008-01-28T05:29)出现了误差变大的情况。综上所述，添加云信息的神经网络模型（C-BPNN和ZBPNN）的结果要明显好于未添加任何云信息的BPNN0模型，且误差波动范围相较于BPNN0模型也更加稳定。从15条样本反演结果上看，C-BPNN模型反演的结果只有一条样本(2008-01-28T05:29)误差大于BPNN0模型的反演结果，而Z-BPNN模型出现3条样本(2008-01-28T05:29、02-29T05:25、02-04T18:53)，对比可知C-BPNN更具有优势。

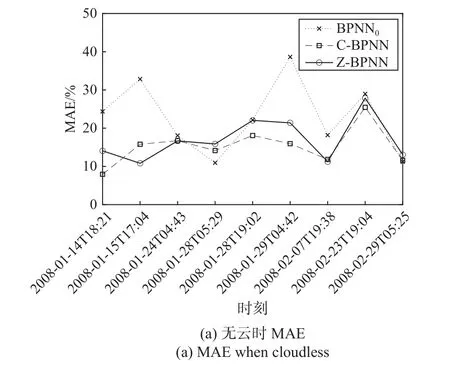
图3 3种模型反演结果MAE与RMSEFig.3 MAE and RMSE of the inversion results for 3 models when cloudless

4 个例分析及算法优化

4.1 无云个例分析

利用3种模型分别对无云条件下2008-01-14T18:21、01-15T17:04、01-28T05:29时反演的相对湿度及其RMSE结果如图4所示。可以看出，第一条样本中C-BPNN模型反演结果相较于其他两种模型更好，第二条样本中Z-BPNN反演结果较好，最后一条样本中BPNN0模型反演结果较好。

图4 无云条件下不同时刻相对湿度及其RMSEFig.4 Relative humidity and its RMSE when cloudless at different times

图4(a)中探空湿度廓线随高度的增加而减小，波动范围也较小，C-BPNN与Z-BPNN模型反演结果都明显好于BPNN0，而BPNN0反演的相对湿度廓线大于实际的相对湿度廓线；图4(d)中，随高度增加，BPNN0模型反演的相对湿度廓线的RMSE呈增大的趋势，直至稳定在30%左右，而C-BPNN与Z-BPNN的RMSE在4 km的高度上才逐渐分离扩大，最终CBPNN RMSE稳定在10%左右，Z-BPNN模型稳定在20%左右；图4(b)中，探空相对湿度廓线变化相对平缓，但3种模型的反演结果都偏大，BPNN0模型在5 km以下偏离程度最大，5 km以上的反演结果最符合实际，而C-BPNN与Z-BPNN模型在整个高度层上的反演结果较为相似；图4(e) 中， Z-BPNN模型的RMSE反演效果最好；图4(c)中实际的探空廓线在7 km以下逐渐减小，在7 km时突然发生跃变，相对湿度接近80%，说明在此高度附近可能有云的形成，但探空气球并未入云，跃变一直持续到9 km结束，只有BPNN0模型识别出了此跃变，而C-BPNN与ZBPNN反演结果相近，且与实际情况偏离较大，导致该样本C-BPNN与Z-BPNN模型反演的整体MAE与RMSE大于BPNN0模型，BPNN输入层的增多导致每个节点的权重发生改变，当高空出现较大的跃变但又不满足入云条件时，添加云信息的模型可能出现无法准确反演出实际变化的情况，因此权值与阈值的选择尤为重要。

4.2 有云个例分析

图5为有云条件下2008-01-29T20:29、01-29T22:05、02-04T18:53的反演的相对湿度及其RMSE，第一条样本中C-BPNN模型反演结果相较于其他两种模型更好，第二条样本中Z-BPNN反演结果较好，最后一条样本中BPNN0模型反演结果好于Z-BPNN模型。

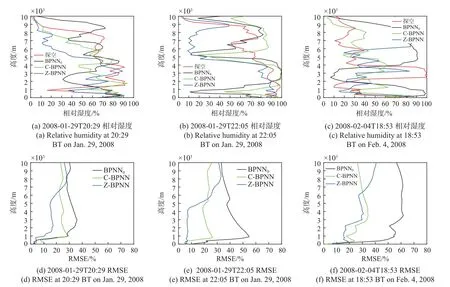
图5 有云条件下不同时刻相对湿度及其RMSEFig.5 Relative humidity and RMSE inversion results with clouds at different times

图5(a)、(b)和(c)中的入云和出云位置分别为1 750~3 890 m、1 345~4 120 m和1 592~2 219 m。图5(a)中，在有云的高度上，C-BPNN与Z-BPNN模型反演的相对湿度更接近于探空廓线，在无云高度时Z-BPNN出现了较大的跃变；图5(d)中的RMSE很好地反映出此问题，在出云高度即3 890 m以下Z-BPNN模型反演结果明显好于C-BPNN与BPNN0模型，出云之后，在无云区域C-BPNN要好于另外两种模型；图5(b)中，在有云的部分，3种模型反演的相对湿度均较接近真实探空廓线；对应的图5(e)中RMSE的反演结果中，有云的高度上BPNN0反演结果却好于C-BPNN与Z-BPNN模型，分析认为该样本探空廓线所反映的云的特征不够明显，从2 km开始相对湿度断断续续小于85%，这可能是探空气球的漂移导致，而添加云信息的两个模型相对湿度接近100%，此处云的存在更加明显，无云高度时Z-BPNN与实际的探空廓线偏差最小，导致ZBPNN反演的RMSE小于另外两种模型； 图5(c)中，C-BPNN与Z-BPNN在有云部分更加接近探空廓线，但在无云区域，BPNN0更接近探空廓线，其次是CBPNN；图5(f)的结果表明随着高度的升高，ZBPNN模型反演结果最差。由6条样本的CBPNN模型反演的湿度廓线与探空湿度廓线的RMSE可知，随着高度的上升，约升高至1 km时RMSE变化范围始终保持在20附近，而BPNN0与ZBPNN模型或多或少出现了大的波动，故C-BPNN模型的稳定性较好。

4.3 算法优化

神经网络初始权值与阈值直接影响反演的效果，由于BPNN是一种局部搜索的优化方法，而网络的权值是通过沿局部改善的方向逐渐进行调整的，容易陷入局部最小值[24]，很难得到最佳的初始权值和阈值。本节通过遗传算法(genetic algorithms,GA)寻找BPNN最优初始权值与阈值，达到优化网络的目的。

20世纪60年代，Holland提出了一种通过模拟生物界自然选择和淘汰的繁衍规律产生的优化算法，即GA，该算法具有良好的并行全局搜索的性能。通过GA找出神经网络前期训练的最优解，再通过BPNN的误差，反向传递计算出具有最高精度的网络权值，用最优的权值进行预测结果，进而改善网络。本文建立的GA优化BPNN模型流程如图6所示。

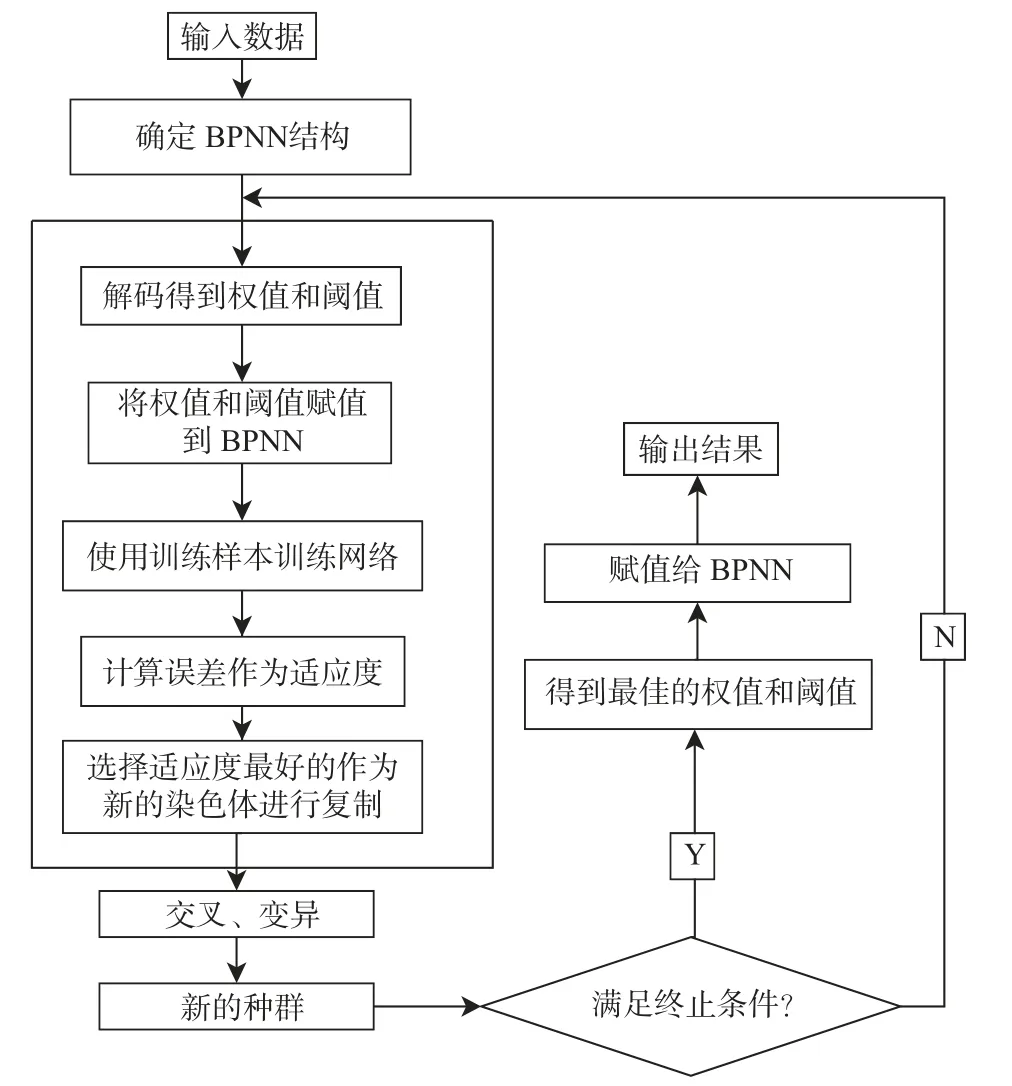
图6 GA优化BPNN模型流程Fig.6 Flow of the model optimized by GA

以BPNN0模型为例，首先输入15个参数确定BPNN结构，然后对BPNN进行编码操作，得到初始种群。编码操作又称种群初代化，种群规模设置为20，个体采用实数编码，通过计算输入层和隐含层的连接权值、隐含层的阈值与输出层的连接权值、输出层阈值个数进行叠加，组成一个长度为1 728的个体编码；再通过解码得到初始权值和阈值，将权值和阈值赋值给构建的BPNN，使用样本训练网络；然后将预测输出与期望输出之间的误差绝对值作为个体的最佳适应度，因此适应度越小越好。将最佳适应度对应的染色体进行复制，通过交叉、变异操作产生一个新的种群（交叉和变异率分别设置为0.4、0.1），对比新种群与上一代种群的最佳适应度，择优选取，遗传代数设置为50，循环至迭代结束，最后通过解码得到神经网络最佳的权值和阈值，重新赋值给已经构建好的BPNN中，输出47个高度层的相对湿度。

4.4 GA优化BPNN反演结果

基于第3节中的BPNN，增加了GA，经过50轮遗传迭代，BPNN0模型经优化后的反演结果如图7所示。共15个时刻的样本数据，其中前9个为无云天气，后6个为有云天气，大部分测试样本经GA优化后误差都呈显著下降的趋势，其中2008-01-14T18:21、01-15T17:04、01-29T04:42三条样本下降幅度在50%左右，但也有两条无云样本(01-28T05:29与02-29T05:25)出现明显增加，其中01-28T05:29样本的MAE由10.942 5%增大到17.023 1%，RMSE由14.100 8%增大到21.955 7%；02-29T 05:25样本的MAE由11.213 6%增大到16.067 8%，RMSE由20.204%增大到25.159 2%。

图7 BPNN0模型经GA优化后反演结果的MAE和RMSEFig.7 MAE and RMSE of BPNN0 model inversion result optimized by GA

C-BPNN模型经GA优化后反演结果的MAE与RMSE如图8所示，经GA优化后的C-BPNN最佳适应度从0.172 2下降至0.167 8，下降了6.3%。图8(a)反演结果的MAE对比中有11条样本具有明显优化效果，图8(b)RMSE反演结果对比中有12条样本具有明显优化效果，最大优化样本(01-19T05:44)较优化前MAE由19.870 4%减小至7.704 9%，RMSE由25.797 2%减小至9.978 3%，3条样本出现小幅度上升(01-14T18:21、02-29T05:25和01-17T05:01)，最差优化样本(01-14T18:21)MAE由7.964 6%上升至11.096 9%，RMSE由11.392 5%上升至13.967 7%。

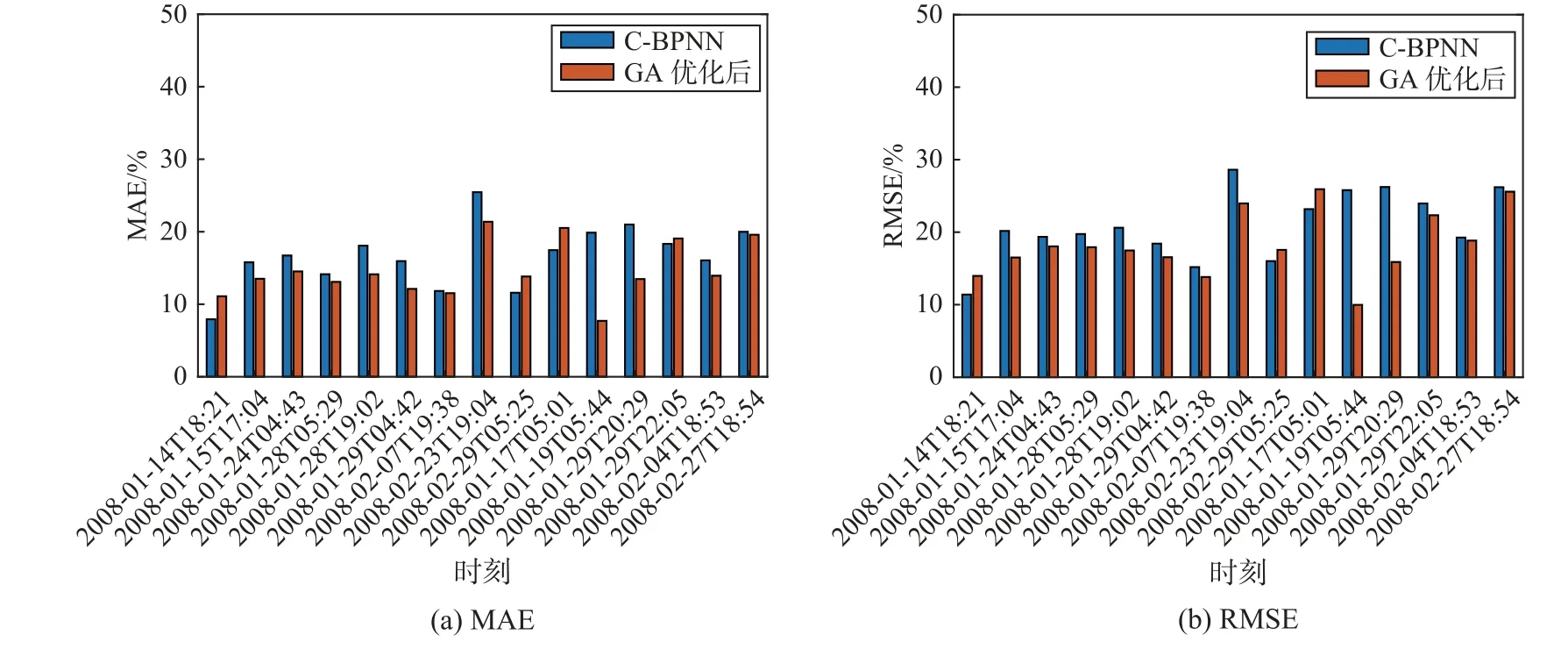
图8 C-BPNN模型经GA优化后反演结果的MAE和RMSEFig.8 MAE and RMSE C-BPNN model inversion result optimized by GA

Z-BPNN模型经GA优化后反演结果的MAE与RMSE如图9所示。可以看出，经GA优化后的ZBPNN最佳适应度由0.127 8下降至0.120 5，下降了5.7%，但优化效果却不明显，MAE有8条样本出现上升，RMSE有7条样本出现上升，可能是其权值与阈值个数过于庞大，高达5 327个，而BPNN0与CBPNN模型仅有1 711和1 829个。实际上，在有云条件下，雷达反射率因子的强度与相对湿度并不存在正相关，只要有云存在相对湿度就会大于85%，云的强弱对相对湿度影响不大。综上所述，经GA优化后的BPNN0与C-BPNN模型反演误差显著减小，对Z-BPNN优化效果并不明显，因此在实际应用过程中添加入云和出云的高度，建立C-BPNN模型效果最理想。

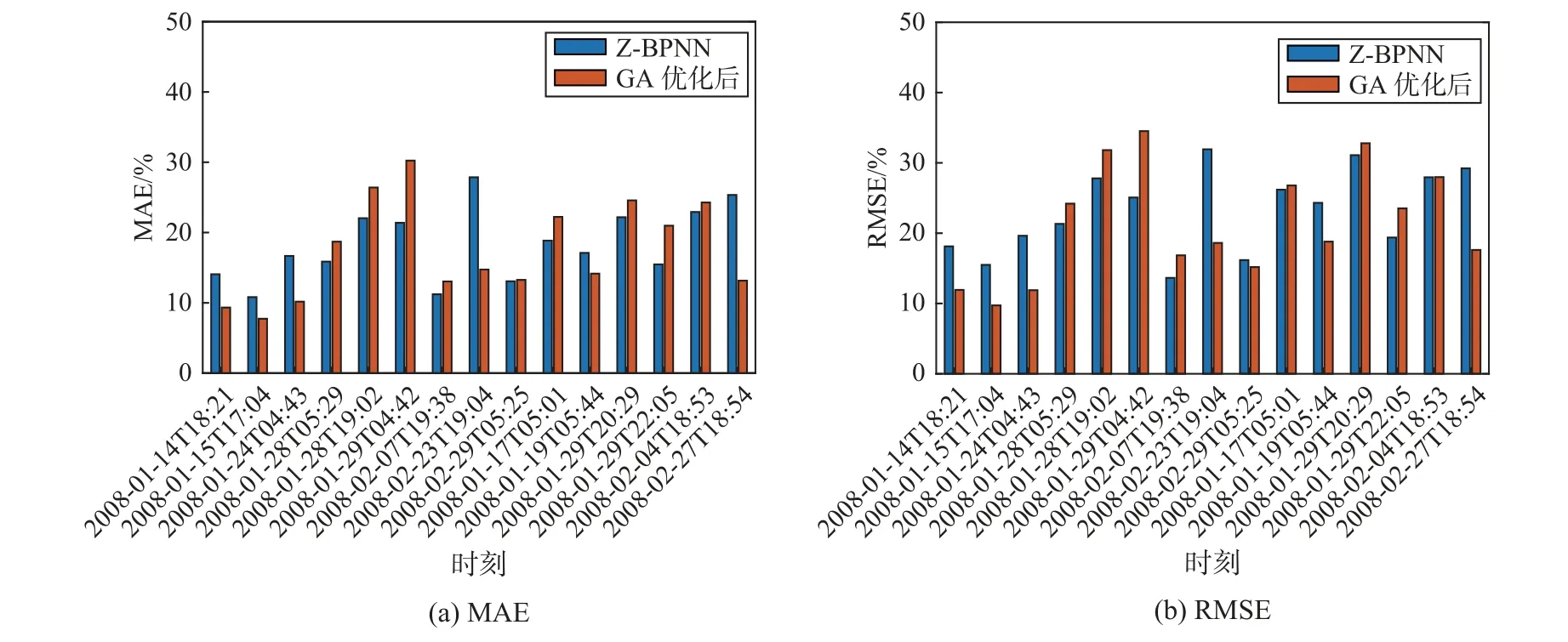
图9 Z-BPNN模型经GA优化后反演结果的MAE和RMSEFig.9 MAE and RMSE of Z-BPNN model inversion result optimized by GA

5 结 论

通过ARM大气观测网站提供的毫米波测云雷达、微波辐射计以及对应时段的探空数据，分别建立了添加不同云信息的BPNN反演模型与未添加任何云信息的BPNN模型，并对比分析了3种不同模型的反演情况。在对3种模型反演结果最好的个例进行时分析发现神经网络模型对初始权值与阈值较为敏感，因此通过GA对BPNN模型进行优化，得到以下结论：

1)从15条测试样本反演结果可知，添加不同云信息的C-BPNN与Z-BPNN模型反演结果好于未添加云信息的BPNN0反演模型，相较于BPNN0模型，C-BPNN模型最大MAE减小22.695 8%，RMSE减小27.773 5%；Z-BPNN模型MAE减少17.255 9%，RMSE减少21.114 4%。

2)从不同高度层的RMSE反演结果可知，CBPNN模型在反演相对湿度廓线上具有更好的稳定性，RMSE随着高度的升高，始终保持在20%左右，而Z-BPNN模型与BPNN0模型反演结果出现不同程度的跃变。

3)从建立的GA优化3种BPNN模型反演结果可知，BPNN0模型得到显著优化，MAE与RMSE有不同程度的减小；C-BPNN模型中有12条样本呈现不同程度改善，3条误差变大的样本，但增加幅度较小；而Z-BPNN模型反演的RMSE既有增大，也有减小，且波动幅度偏大。

反演结果对后续的研究具有一定的参考意义，但由于受限于样本数量，导致实验结果缺乏一定的普适性。下一步工作将继续收集样本，并在后续工作中加入对地基微波辐射计二次产品的反演。