一种整数抽取结合小数插值重采样技术研究

单长胜，尹曙明，郑哲，郝利云

（1.北京空间信息传输中心，北京 102300；2.北京理工大学，北京 100081）

0 引 言

射频直采是指将天线接收到的射频信号经过限幅、滤波、放大后直接送入高速ADC 采样，其降低了系统的硬件复杂度，减少了模拟器件引入的噪声，改善了通道的一致性。近年来随着相控阵雷达、高速信号转换及信号处理等技术的飞速发展，促进了射频直采技术的逐步工程应用。然而射频直采信号数据率极高，导致后续信号传输与处理难度大幅上升［1］。数字重采样技术是缓解数字信号处理压力的重要手段，采用数字重采样技术可以降低射频信号采样率，进而有效地实现信号的传输、处理和存储。

数字重采样可分为整数倍重采样与分数倍重采样两类［2］。整数倍重采样包括整数倍抽取与内插，相关理论成熟。分数倍重采样包括简单分数重采样与基于小数插值的数字重采样。简单分数重采样采用抽取级联内插的方式实现分数倍采样率转换，但该方法仅适用于分子分母较小的场景，无法解决固定射频采样率下精确变采样率变换的需求；基于小数插值的数字重采样方法多采用分段多项式插值逼近理想低通滤波器，对信号直接进行小数插值，从而实现任意倍采样率转换。基于小数插值的数字重采样方法灵活性高、适用性强，在信号处理领域得到了广泛应用。整数倍重采样只适用于射频采样率与目标采样率成整数倍的场景，具有很大的局限性。简单分数重采样实现简单，但无法处理大分子分母的复杂分数倍重采样。基于小数插值的数字重采样方法理论上虽然可以实现任意倍采样率转换，然而对射频采样信号直接进行小数插值时，需要在射频采样率下对信号进行实时处理，难度大，尤其是当射频采样频率几个GHz 时，往往需要几十路进行并行处理，且每路均需小数插值运算，将直接导致工程中几乎无法实现。此外，基于小数插值的数字重采样方法多采用Farrow 结构实现，然而Farrow 结构内插滤波器面对大抽取因子时，带外噪声滤除能力差，低信噪比条件下将直接导致重采样输出信号品质恶化。综上，本文提出了一种整数抽取结合小数插值重采样法来实现任意倍数字重采样方法的转换。

1 整数抽取结合小数插值的数字重采样方法

考虑到直接采用并行结构小数插值数字重采样将极大的消耗资源［3］，且无用的带外噪声抑制差，本文给出一种整数抽取结合小数插值的数字重采样方法。采用该方法首先可有效地降低数据率，减少并行处理难度，节省乘法器资源；其次，采用该方法因先进行了整数抽取，直接地降低了小数插值的输入数据率，从而将Farrow 结构内插滤波器频率响应降低，可提高对带外噪声的滤除能力。整数抽取结合小数插值的数字重采样结构如图1所示。

图1 整数抽取结合小数插值数字重采样示意图

图1中,x(NsnTs)，x((Nsn+1)Ts),…,x((Nsn+N- 1)Ts)为输入数据，h(Ns∕2 - 1)…h(j)…h(0)为半带滤波器系数，g(nThb)为半带抽取后输出，c0(-N∕2)，c0(-N∕2 + 1)，…，cM(N∕2 - 1) 为小数延时滤波器系数，un为当前输入采样点时刻与下一个重采样点输出时刻的时间间隔除以输入采样周期。log2D级整数抽取采用半带滤波器对多路并行信号进行抽取滤波。滤除大量带外噪声的同时将射频采样率fs降为fhb；多级整数抽取后，在低采样率下采用Farrow 结构将小数插值采样率变换为目标采样率fsb。fs、fhb与fsb满足

2 整数抽取结合小数插值重采样理论模型

假设Thb=DTs，Tsb=(1 +p)Thb，则Tsb=D(1 +p)Ts。其中D为整数，0 ＜p＜1，Ts、Thb与Tsb分别为射频采样周期、多级抽取滤波后采样周期以及基带采样周期。x(nTs)经抗混叠滤波器滤波得到

其中，hD(t)为抗混叠滤波器冲激响应，等效为多级滤波器级联，即滤波器频率响应HD(ejw)满足下式：

式中，Hhbi(ejw)为第i级抗混叠滤波器频率响应，将x'(nTs)进行D倍抽取得到

经抽取后采样率变为fhb，采用Farrow 结构进行1 +p倍的小数插值，因此采用分段多项式插值逼近理想低通滤波器时，分段多项式间隔变为Thb。其基函数化为

对g(nThb)进行小数插值可以得到

式中，N′1= -N∕2,N′2=N∕2 - 1。将式（4）代入式（8）可以得到

上式即为整数抽取结合小数插值数字重采样理论模型［4-5］。

2.1 整数抽取结合小数插值参数递推解算方法

多级整数抽取后，一般并行多路信号只剩一路。直接进行串行时间参数递推即可。由式（9）可知，输出采样点所需时间参数um为

同样采取在小数插值输入时钟域下更新时间参数un，则将Tsb=(1 +p)Thb代入下式：

由un的物理意义可知，un∈[0,1 +p)，因此上式可以转化为

2.2 多级整数抽取滤波器选择

典型的多级抽取滤波采用CIC 作为前级滤波器，因其系数全为1，无乘法计算，但当处理射频直采信号时，将CIC放在第一级会存在以下问题：

1）反馈递归结构并行实现难度大及数据溢出

CIC 的典型结构由积分器和梳妆滤波器构成，如图2给出的CIC滤波器的3级级联结构。积分器是一种带有反馈的递归结构，FPGA 实现时无法使用并行的方法降低积分器的工作频率，这就决定了该结构极其不适用于射频直采输出高速率信号的前级滤波。在数字滤波过程中，积分器不断累加，积分器输出信号逐渐增大，存在输出信号位宽确定的情况下数据溢出的问题，需要采用等时间间隔的复位在数据溢出前对积分部分的寄存器进行复位，增加了滤波器设计的复杂度。

图2 CIC抽取滤波器三级级联结构

2）CIC通带衰减问题

CIC 滤波器的直接实现结构虽然不存在反馈递归结构，但单级CIC 滤波器阻带衰减小，无法有效地滤除带外量化噪声及其他噪声，若采用多级级联方式，通带衰减又会增大，当宽带信号经过CIC 低通滤波，可能会造成信号频谱的恶化，尤其是对于调制信号来说，恶化的频谱会严重影响系统的性能［6］。通常采用CIC 滤波器与内插二阶多项式（Interpolated Second Order Polynomial, ISOP）级联的方法减少通带的衰减。但通过级联ISOP补偿滤波器改善通带衰减，就必须付出更多的级数，这样就失去了CIC 滤波器相对于半带滤波器和FIR滤波器的最大优势。

综上，射频直采信号采用CIC作为多级抽取滤波器有着诸多劣势。而半带滤波器不存在反馈结构，可以通过并行处理及流水线技术实现高速抽取滤波，且其近一半系数为零，减少了近3∕4 的乘法运算和近一半的加法运算，另外，半带滤波器还具有通带平坦度高、阻带衰减大的优点，在进行抽取滤波运算时，不会造成信号频谱的恶化及重叠。因此，综合考虑本文采用半带滤波器作为多级抽取滤波器。

3 仿真验证

仿真实验1：输入带宽为8 MHz，载波中心频率2 250 MHz 线性调频信号，以射频采样率3 GS/s 采样输出16 路并行信号，对16 路并行信号正交下变频后，首先以7级14阶半带滤波器对其进行128倍抽取滤波，将采样率降到23.437 5 MS/s；然后经3阶拉格朗日插值的Farrow 结构将采样率转换为20.48 MS/s。仿真结果如图3所示。

图3 整数抽取结合小数插值重采样输出信号频谱

实验表明，整数抽取结合小数插值的重采样方法，有效融合了整数采样技术的成熟高效优势和小数插值的灵活性优势，兼顾了射频直采的复杂性和灵活性需求，具备工程可行性。

仿真实验2：分别输入信噪比为30，10，0和-10 dB 的线性调频信号，信号参数及抽取滤波操作与实验1 相同，在4 种信噪比下的仿真结果如图4所示。

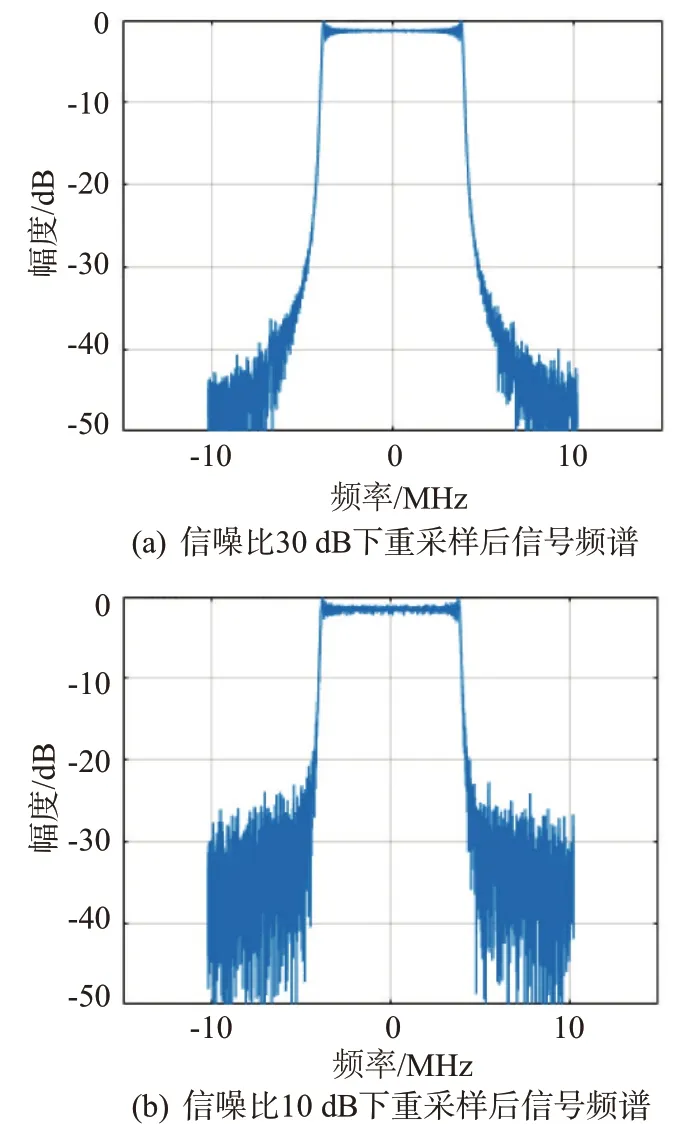
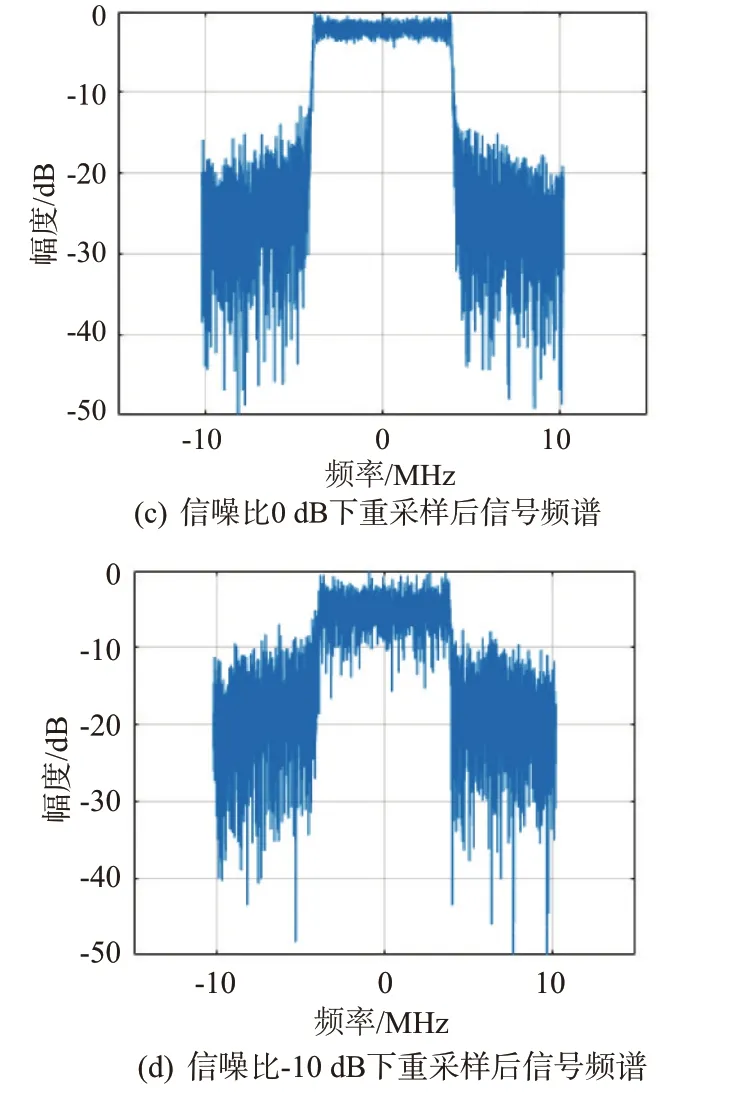
图4 不同信噪比下整数抽取结合小数插值重采样输出信号频谱

实验表明，本方法在0 dB 信噪比情况下，仍具备较好的重采样输出信号品质，可应用于低信噪比条件下的信号采样。

4 结束语

本文针对射频高速率采样需求，开展了数字重采样技术研究，提出一种整数抽取结合小数插值的数字重采样方法。由理论与仿真结果可知，该方法可以实现射频信号复杂分数倍数字重采样精确调整。且通过整数抽取将小数插值滤波器的输入采样率降低，使得Farrow 内插滤波器的频率响应零点接近于目标采样率，改善了带外噪声滤除能力。在信噪比相同的情况下，整数抽取结合小数插值的数字重采样输出信号质量更好。

与传统整数结合简单分数抽取相比，该方法可实现大范围精确变采样率变换，具有更大的普适性。与直接小数插值方式进行变采样率相比，可极大地降低后续信号处理的并行度，且改善了带外噪声。